基于多任務高斯過程模型的短期負荷預測研究

朱維娜

摘要：電力負荷預測是電網調度的重要問題之一。本文研究一種基于多任務高斯過程，包含曲線聚類的回歸模型在短期負荷預測上的應用，該模型可以利用非齊次的相似日負荷數據同時完成多任務學習、聚類與預測。通過實例分析，表明了該模型在基于相似日聚類的短期預測上具有一定的可行性及有效性，為研究短期負荷曲線聚類與預測提供了新的模型參考。

關鍵詞：電力負荷? 多任務? 高斯過程? 曲線聚類

中圖分類號：TM715

Abstract： Power load forecasting is one of the important problems of power grid dispatching. This article studies the application of a regression model based on multi task Gaussian process including curve clustering in short-term load forecasting. The model can use non-homogeneous similar daily load data to complete multi task learning， clustering and forecasting at the same time.? The example analysis shows that the model has certain feasibility and effectiveness in short-term forecasting based on similar days clustering， and provides a new model reference for the study of short-term load curve clustering and forecasting.

Key Words： Power load; Multi-task; Gaussian process; Curve clustering

隨著我國電力大數據建設的持續推進，電力負荷數據可以被實時的高頻采集存儲，一段時間內的多組負荷數據近似于具有某些共同結構但包含噪聲的函數對象，聚類作為數據挖掘的重要方法之一，對于負荷的函數型聚類分析也稱為負荷曲線聚類分析，在近年來成為負荷預測研究的一個熱點方向[1，2]。

目前負荷曲線聚類預測有直接聚類和間接聚類，直接聚類是基于原始負荷數據直接對曲線聚類，如有研究[3]使用GMM聚類算法對智能電表用戶分季節聚類，結合聚類結果預測負荷;間接聚類針對高維的負荷數據先做降維處理再聚類，相關研究[4]中先利用PCA算法將負荷數據降維至可視化的三維，確定聚類算法的最佳類數和k-means聚類的初始聚類中心后，再使用智能電網用戶的數據進行聚類。本文研究的是一種基于自適應模型的直接聚類[5]，由于短期負荷曲線具有較大的隨機性，較符合高斯過程，而高斯過程憑借可以提供預測值不確定性分析等優點，已在多個領域已有廣泛應用，該模型還結合了機器學習的多任務學習思想，充分利用了數據的共享信息，且對于非齊次的數據比較友好，可以適應實際中經常面臨的數據不完整問題。

短期負荷預測受到天氣、節假日等多種因素的影響，許多學者會基于相似日對負荷進行聚類預測，如有研究[6]在對鋼鐵企業的電力負荷做預測時考慮了生產工況存在的日相似性，對相似日聚類后結合優化算法預測，取得較好的效果。由于節假日大部分生產活動的不確定性較大，因此本文主要研究工作日的短期負荷預測。

1模型介紹

1.1多任務高斯聚類回歸模型

對于一天內的負荷曲線，模型結構定義如下：

其中表示條負荷曲線，假定聚類數目為類，以潛變量表示第條負荷曲線屬于類的概率，服從多點分布。

表示劃分為第類的負荷曲線的均值函數，假定均值函數服從高斯過程，記為，其中是第個高斯過程的均值函數，是第個高斯過程關于超參數的協方差核函數。

是第條負荷曲線的個體特征函數，假定個體特征函數也服從高斯過程，記為，其中是第個高斯過程關于超參數的協方差核函數。

是隨機誤差項，也服從一個高斯過程，記為，其中是第條負荷曲線函數的方差。

模型中的協方差核函數均用指數二次核來刻畫，這是一種在包含高斯過程的文獻中常見的核，這個核取決于兩個超參數，核的形式如下：

1.2參數估計與預測

該模型的參數估計主要采用變分EM算法，變分方法已被證明非常適用于復雜高斯過程問題的推理[8]。

在該模型中，假設對于任意的和都有、、、相互獨立，通過在訓練樣本數據對數似然和潛變量的分布之間引入KL散度，獲得訓練樣本數據對數似然的一個下界，這個下界與潛變量的分布 和超參數集合有關，在潛變量和相互獨立的假設下，可以分別計算出和真實超后驗分布的解析近似和，其中，。接下來在變分EM算法的E步根據這個下界來更新和的解析近似分布和，在M步中最大化這個下界以優化超參數，迭代E、M這兩個步驟直至收斂，即可估計出超參數集合。

對于一條新的負荷曲線，根據已知部分觀測值，預測其他時間點的負荷，首先在已估計出均值函數的基礎上，擴展時間點為增加預測時間點的，即可得到覆蓋所有時間網格點的均值函數，此時僅需采用EM算法，根據新個體已知的部分觀測值和均值函數，在E步估計出新個體的潛變量的后驗分布，再通過M步更新這個新個體的超參數，迭代E步和M步直至收斂即可估計出新個體的所有參數。最后基于新個體屬于每一類的概率對均值函數進行加權計算，就得到了最終的預測結果。

2實例分析

選用美國電力公司2021年9月9日至10月7日的除去非工作日共22d的實時負荷數據，采集頻率為5min/每次，數據來源于PMJ電力市場官網公開的電力負荷數據集，存在輕度缺失。由于該模型有多個高斯過程，訓練模型的時間復雜度較高，僅選用15min粒度負荷數據，最終得到了22條在時間上有96維且存在少量缺失值的負荷數據。

按照時間順序，選擇前21條負荷數據作為訓練樣本，第22條曲線作為新個體，即10月7日的負荷曲線，將新個體前80個時間點的負荷作為已知數據，后16個時間點（4h）作為待預測時間點。

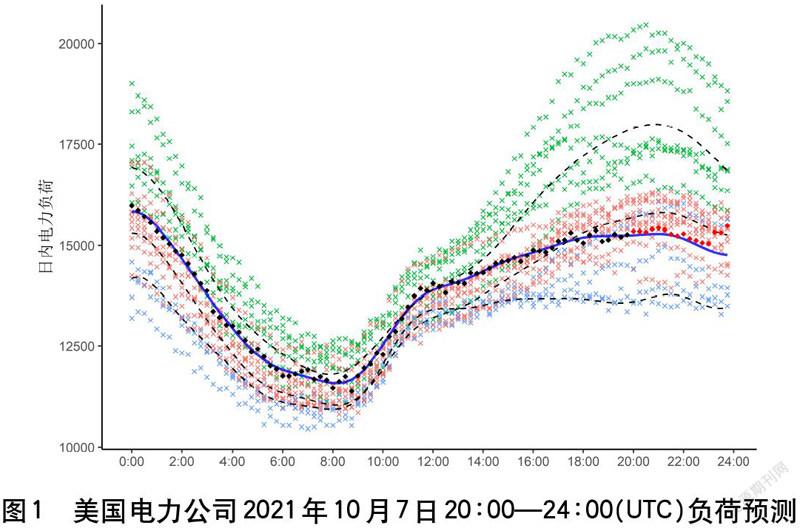
首先初始化模型的參數：結合曲線形態設置聚類數目，設每個均值函數所服從高斯過程的均值為0，協方差核的超參數，每個個體特征函數所服從高斯過程的協方差核的超參數，每條負荷曲線方差。然后用訓練樣本數據訓練模型，模型經過兩次迭代后收斂，用時35s。最后第22條負荷曲線的已知數據帶入訓練好的模型估計新個體的參數，模型經過6次迭代后收斂，用時7s，即可得出新個體包含待預測時間點的負荷曲線函數，結果如圖1所示。

圖1中的藍色曲線即為新個體的負荷曲線，以20：00為界，前半段是對新個體已知負荷數據的（黑點）擬合，后半段是對待預測時間點負荷數據（紅點）的預測，用3種不同的顏色區分被聚成的3類訓練樣本數據，虛線表示每個類的均值函數。如圖1所示，預測結果十分接近美國電力公司10月7日20：00-24：00的真實負荷，除了對真實負荷尾部波動的預測不夠好，但該波動也可能受其他因素的影響，以下是對該模型的進一步探索。

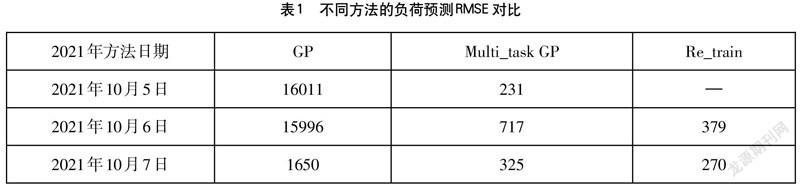
表1的每行分別是對美國電力公司10月5日、10月6日和10月7日在20：00-24：00時間段的16點負荷預測RMSE，第一列是用單一高斯過程（GP）的方法，僅基于新個體當天20：00前的80個負荷數據做預測，第二列和第三列都是用本文介紹的多任務高斯過程（Multi_task GP）的方法。區別在于：第二列選擇10月5日前的負荷數據訓練模型，然后基于該模型分別對3條新曲線做預測，而第三列在預測10月6日和10月7日的負荷曲線時，分別加入了前一天和前兩天的負荷數據重新訓練模型后再預測。如表1所示，第一列的預測RMSE遠大于第二列，第三列的預測RMSE略小于第二列。這表明，對比單一高斯過程模型，該模型在處理這個短期負荷預測的問題上有顯著優勢，而且新的負荷曲線數據的加入可能會進一步提升該模型的預測效果。

3結語

本文利用美國電力公司的工作日15min 粒度負荷數據研究了一種多任務高斯過程的聚類回歸模型在短期負荷預測上的表現。通過多次對比發現，在這個短期負荷預測問題上，該模型的預測負荷與實際負荷基本吻合，在對比單一高斯過程模型時具有突出優勢，且加入新的負荷曲線數據重新訓練模型可能會對該模型的預測效果有提升作用，為研究短期負荷的精準預測提供了有價值的模型參考。

參考文獻

[1]鄧威，郭釔秀，李勇，等.基于聚類及趨勢指標的長短期神經網絡配網負荷短期預測[J].湖南電力，2021，41（4）：27-33.

[2]魏勇，李學軍，李萬偉，等.基于空間密度聚類和K-shape算法的城市綜合體負荷模式聚類方法[J].電力系統保護與控制，2021，49（14）：37-44.

[3]薛琳.基于用電行為分析的低冗余特征配電網短期負荷預測研究[D].吉林：東北電力大學，2019.

[4]吳孟林.智能電網中居民用戶聚類與短期負荷預測研究[D].重慶：重慶郵電大學，2019.

[5] Leroy Arthur，Latouche Pierre，Guedj Benjamin and Gey Servane.Cluster-Specific Predictions with Multi-Task Gaussian Processes[EB/OL].（2020-11-17）.[2021-10-22].https：//arxiv.org/abs/2011.07866v2.

[6]胡函武，楊英，魏晗，等.短期負荷預測方法綜述[J].電子世界，2018（20）：109.

[7]李維鈞.基于相似日聚類的鋼鐵企業電力負荷預測[D].大連：大連理工大學，2021.

[8] Hensman James，Fusi Nicolo and Lawrence Neil D.Gaussian processes for big data[EB/OL].（2013-9-26）.[2021-10-22].https：//arxiv.org/abs/1309.6835.

3171500338299