工業機器人摩擦補償方法研究

殷興國

摘要：關節摩擦力是影響工業機器人的運動平穩、碰撞檢測的靈敏性及拖拽示教的平滑性的關鍵因素，如何確定摩擦力的大小是工業機器人的控制難點。針對工業機器人摩擦力的計算和補償問題，本文在傳統魯棒自適應方法的基礎上引入權重因子，實現一種基于角色切換的摩擦補償，進而提出了兩種有效的自適應摩擦補償方法，并證明了其在控制器應用中的穩定性，最后在連桿系統中用仿真的方法驗證了兩種補償方法的有效性，并比較了它們的優缺點。

關鍵詞：工業機器人摩擦補償自適應連桿系統

Abstract： Joint friction is the key factor affecting the motion stability of industrial robot， the sensitivity of collision detection and the smoothness of drag teaching. How to determine the friction is the difficulty point of industrial robot control. Aiming at the problem of friction calculation and compensation of industrial robot， based on the traditional robust adaptive method， this paper introduces the weight factor to realize a friction compensation based on role switching， then proposes two effective adaptive friction compensation methods， and proves their stability in the application of controller， Finally， the effectiveness of the two compensation methods is verified by simulation in the connecting rod system， and their advantages and disadvantages are compared.

Key Words： Industrial robot; Friction compensation; Adaptive; Connecting rod system

隨著近些年機器人摩擦補償方法研究的不斷深入，機器人摩擦補償方法也多種多樣。實際上，機器人摩擦補償方案的選取受到許多因素的影響，包括可用的執行器信息、傳感器信息等。因此，以不同的可用摩擦信息作為依據，本文詳細闡述機器人摩擦補償的研究進展。

假設摩擦模型是已知的并且參數可以被得到，此時，人們可以通過摩擦參數辨識的方法實現機器人摩擦的補償。基于給定的摩擦模型，人們可以采用離線的機器人摩擦參數辨識方法，并根據辨識好的參數在工程中實現機器人的摩擦補償[1，2]。摩擦力模型主要經歷了庫倫摩擦模型、靜摩擦+庫倫摩擦模型、Stribeck模型和LuGre模型等[3]，吳曉敏等在Stribeck模型基礎上加入了溫度項[4]，Johanastrom等在LuGre模型基礎上分析粘滑運動[5]，此外，針對模型參數皆已知的動態摩擦模型[6]，Kosti等運用觀測器的方法觀測動態摩擦模型的內核態，實現固定模型、參數的動態摩擦補償[7]。不僅如此，還將魯棒方法導入機器人模型的獲取中，從而在已知模型的基礎上，令人滿意地補償機器人中的摩擦力[8]。

針對摩擦模型已知，但參數未知的情況，自適應方法是補償摩擦的一種常見方案[9]。對于摩擦模型未知的情況，人們常常將魯棒方法應用于機器人的摩擦補償。此外，一些先進的智能工具也被使用到機器人摩擦補償的方案中。模糊、神經網絡[10-12]、強化學習[13]等智能工具通過構建機器人摩擦模型或者自調節控制參數等方法[14]，對機器人的摩擦進行補償。

然而，對于上述的絕大部分摩擦補償方法而言，摩擦被視為一種有害于機器人系統穩定的擾動，對其進行補償。但實際情況下，摩擦并不一定有害于系統的穩定。出于利用摩擦穩定系統的考慮，本文在傳統魯棒自適應方法的基礎上引入權重因子，實現一種基于角色切換的摩擦補償。

針對模型已知參數未知的靜摩擦，引入了權重因子，并將其運用在基于模型的兩種機器人魯棒自適應摩擦補償方法中.通過權重因子，一方面，當摩擦有害于機器人系統穩定時對摩擦進行補償抵消;另一方面，當摩擦有益于系統穩定時，對摩擦進行利用。最后，通過仿真驗證了引入權重因子后，魯棒自適應摩擦補償方法能夠減小跟蹤誤差以及控制力矩。

2系統建模

考慮機器人動力學模型，有一些常見的可用于控制律設計的性質，主要歸納為以下幾點。

第一，慣量矩陣的正定性。

在大多數摩擦補償的方法中，摩擦常常被當作一種有害的因素進行抵消或者補償。但是在很多實際工況中，摩擦常常有利于系統的運動，例如，機械臂可以利用摩擦進行制動。在機器人軌跡跟蹤中，摩擦所扮演的角色也不僅僅是有害者，有時候摩擦也能利于機器人的軌跡跟蹤。而如何判定摩擦在機器人跟蹤軌跡中是有益還是有害，并以此為依據設計控制律，從而實現，一方面，在摩擦有益之時利用摩擦，另一方面，在摩擦有害之時補償摩擦，是本部分重點關注的問題。而摩擦利用的判據與機器人系統李雅普諾夫的穩定性緊密相關。在這里，考慮對摩擦有利或者有害的判據設定為，摩擦是否能夠保證給定擬李雅普諾夫函數的導數始終不大于0，并以此為依據，設計連續的權重因子，并提出魯棒自適應框架下的基于角色切換的機器人摩擦補償方法。

考慮基于關節空間的機器人動力學模型可以描述為如下歐拉-拉格朗日方程的形式，并將摩擦力顯式表達出來，如下：

其中，是機器人在關節空間中的坐標，為機器人慣量矩陣，表示機器人柯氏力與離心力，表示機器人重力，表示機器人摩擦力，表示各關節輸入力矩，為機器人雅各比矩陣。

第四，摩擦中的權重因子設計。

在大多數情況下，摩擦阻礙物體的相對運動或者相對運動趨勢。據此對機器人中的摩擦力方向提出如下合理假定：

下面對權重因子的設計思想進行詳細闡述。

當摩擦力使系統靠近滑模面時，摩擦力有利于系統的穩定，權重因子設定為0。

當摩擦力使系統狀態遠離滑模面時，摩擦力不利于系統的穩定，權重因子設定為1。也就是說，權重因子可以根據摩擦力在軌跡跟蹤中所扮演的角色，即有益者或者有害者，適時并連續地取值，從而達到，一方面，在摩擦有益于穩定之時利用摩擦，另一方面，在摩擦有害于穩定之時補償摩擦的效果，因而可以實現控制律利用摩擦和補償摩擦的角色切換。

在實際工程中，受到不同機械結構、環境、任務等因素的影響，人們所能得到的機器人摩擦信息不盡相同。很多情況下，機器人摩擦的模型很難準確得到。據此，根據摩擦模型能否準確得到，本文分別設計基于摩擦模型的魯棒自適應摩擦補償和不基于摩擦模型的魯棒自適應摩擦補償。兩者均是J.J.Slotine提出的機器人自適應補償框架下進行摩擦補償的。

考慮庫倫-粘性的靜態摩擦模型：

與機器人動力學參數可線性化類似，摩擦參數線性化的形式可以推導為：

雖然說摩擦模型可以得到，但是摩擦參數可能存在一定的誤差，即精確的的值很難得到。不僅如此，機器人動力學參數也存在不確定性，即人們很難得到精確的的值。因而，鑒于機器人動力學和摩擦均存在一定的參數不確定性，本文提出下述定理。

2.1使用速度信息的自適應摩擦補償方法

考慮機器人動力學模型和摩擦模型。假定機器人摩擦滿足假設，那么提出控制律：

即各關節軌跡誤差趨于下述滑模面：

所以跟蹤位置、速度誤差漸近收斂到0，定理證明完畢。

結合權重因子和自適應控制律，對角色切換進行詳盡分析。

（1）當時，結合假設，中關于摩擦的項可能不小于0，此時無法保證機器人跟蹤軌跡的穩定性，需要對摩擦項進行處理。因而選取。當時，該控制律與傳統的基于模型的魯棒自適應摩擦補償方法相同，此時摩擦有害于機器人軌跡跟蹤的穩定，因而采用自適應的方法抵消摩擦。

（2）當時，結合假設，中關于摩擦的項不大于0，此時即使對摩擦不做處理，機器人軌跡跟蹤的穩定性也能得到保證。當時，控制律中與摩擦相關的項將不作用于系統的控制力矩?？刂坡蔁o需對摩擦進行處理，此時的摩擦將有利于機器人軌跡跟蹤的穩定。當時，對摩擦的處理介于上述兩者之間，目的是保證控制律的連續性。

注意到定理一的證明不涉及矩陣A和矩陣B。這意味著，該摩擦力補償方法不僅能應用于庫倫-粘性靜態摩擦模型。只要摩擦模型滿足參數線性化性質和假設，權重因子就可以引入到基于摩擦模型的魯棒自適應補償方法中，從而實現基于角色切換的摩擦補償。例如，在Stribeck模型線性參數未知而非線性參數已知的情況下，該基于角色切換的摩擦補償方法同樣適用。

為了減少摩擦角色切換中產生的抖振現象，本方法在權重因子中引入了邊界層，以保證切換過程的連續性。對于大多數引入邊界層來減少抖振的控制律，系統嚴格意義上的漸近穩定性難以保證，閉環系統最終收斂到平衡點的有界鄰域內。而在本方法中，邊界層的引入只改變了利用摩擦與不利用摩擦的作用區間，雖然會影響角色切換的效果，但是并不影響摩擦補償的穩定性，機器人系統嚴格意義上的穩定性仍能得到保證。

該方法針對的是機器人摩擦參數未知的情形。如果摩擦參數精確已知時，亦可以將權重因子運用在摩擦的精確抵消上。通過權重因子的引入，我們只需要精確抵消不利于機器人軌跡跟蹤穩定時的摩擦即可。

在實際的機器人摩擦補償中，權重因子的引入將帶來更多的可調節參數。本方法可以通過設計權重因子中和的值，來合理地選取不利用摩擦與摩擦利用的作用區間，從而實現更好的摩擦補償的性能。

注意到上述摩擦補償的方法用到了速度信息。但是在實際機器人系統中，相比位置信息而言，獲取的速度信息會有較大的誤差。不僅如此，速度信息會比位置信息存在更大的噪聲干擾。因而文獻提出了一種通過代替來實現的自適應摩擦補償。而同樣地，權重因子也可以引入到該自適應摩擦補償方法中，作為定理一的補充和擴展。

2.2使用參考速度信息的自適應摩擦補償方法

考慮機器人動力學模型和庫倫+粘性摩擦模型。假定機器人摩擦模型滿足矩陣A與矩陣B的對角元均不小于0，那么提出如下控制律：

所以跟蹤位置、速度誤差漸近收斂到0，定理證明完畢。

定理一與定理二的控制律不同點在于，摩擦補償項里面的自變量由變為了，即定理二中關于摩擦補償的項為，而定理一中針對摩擦補償的項為。雖然如此，該自適應摩擦補償方法仍涉及了速度信息，但這種方法引入權重因子后亦能夠實現基于角色切換的摩擦補償效果。

3連桿系統仿真驗證

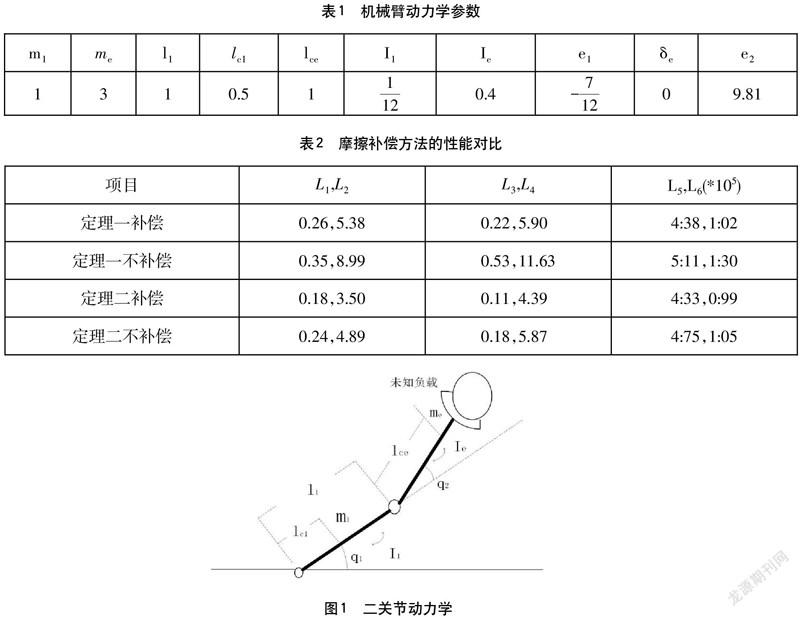
考慮二連桿大負載機械臂抓取模型，如圖1所示。

其他固定的機械臂動力學參數如表1所示。

假定二連桿機械臂受到較大的摩擦。其真實的摩擦模型設定為：

其次，本仿真給出待估計摩擦模型和機械臂動力學模型的初始估計參數。這里待估計的機械臂動力學初始參數與摩擦參數初始值為：

最后設定跟蹤軌跡及控制律參數。機械臂跟蹤的目標曲線設定為：

魯棒自適應參數的值設置如下：

4基于摩擦模型的魯棒自適應摩擦補償仿真

本部分主要描述基于模型的摩擦自適應補償的二連桿大負載機械臂仿真。權重因子中的參數選取為：

與之對應的，不利用摩擦的權重因子選取為1，即對于任意的。那么

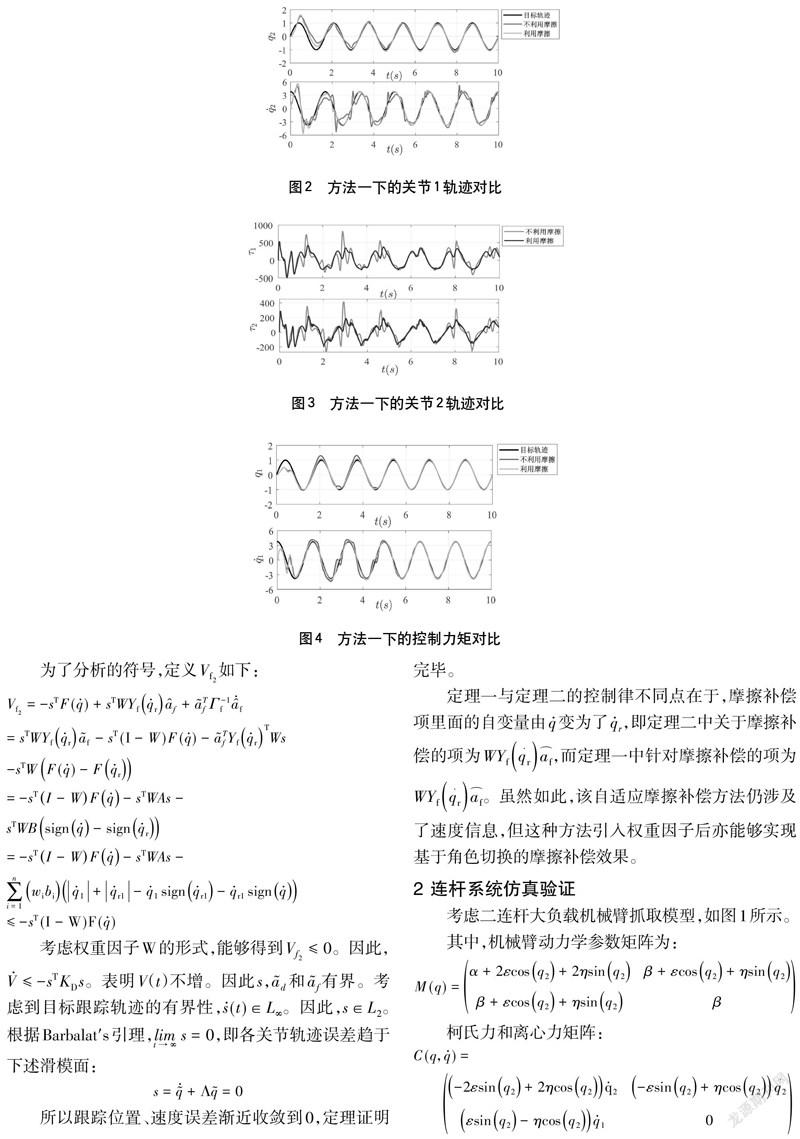
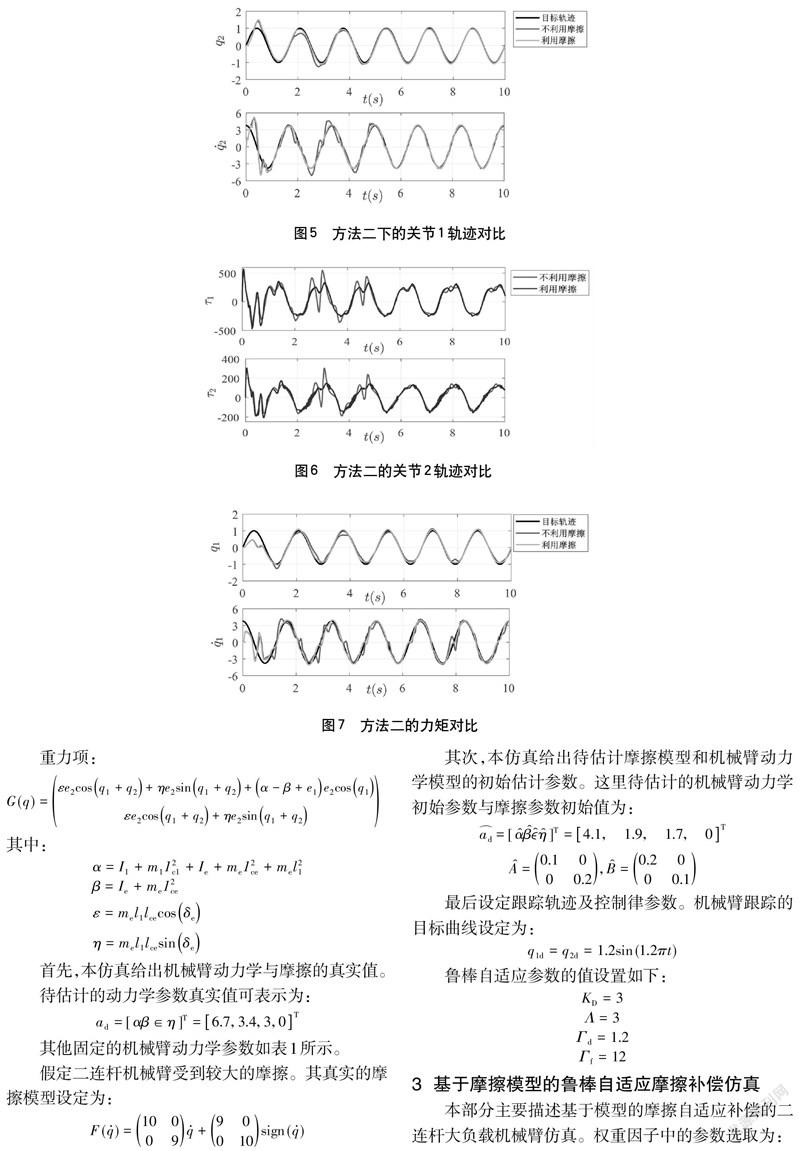
，下列圖2～7中表示了在方法一、方法二控制律下機械臂的位置、速度和力矩。顯然，權重因子的引入不影響機械臂跟蹤的穩定性，機械臂的位置誤差和速度誤差均收斂到0。

為了能夠從數值上更好地描述引入權重因子所帶來的優化效果，仿真取前10s，引入如下表征量：

其中：

可以表征位置和速度的跟蹤誤差，可以表征系統力矩的大小。也就是說，越大，一定程度上意味著機械臂跟蹤位置速度誤差越大;越大，意味著機械臂跟蹤所消耗的能量越大。那么，有無權重因子的仿真效果對比如表2所示。

上表可以清楚地表明，利用摩擦的自適應補償方法所對應的表征量將小于不利用摩擦所對應的表征量。也就是說，從仿真效果上看，基于摩擦模型的角色切換魯棒自適應摩擦補償方法可以實現減小跟蹤誤差和控制力矩的效果。因而，摩擦模型已知的基于角色切換的魯棒自適應摩擦補償，能夠一定程度上提升跟蹤精度，減小控制的能量消耗，因而在工業上有著較強的應用價值。

5結語

本文提出了兩種用于工業機器人控制器中的摩擦補償方法，用理論和實驗仿真的方法驗證了所提出方法的有效性，并通過仿真對比得出魯棒自適應摩擦補償在工業應用上更有優勢。

參考文獻

[1]J.SweversW.Verdonck，J.DeSchutter.DynamicModelIdentificationforIndustrialRobots[J].IEEEControlSystemsMagazine，2007，27：58-71.

[2]儲婷婷.基于多軸耦合同步控制的機器人高精度軌跡跟蹤方法研究[D].哈爾濱：哈爾濱工業大學，2015.

[3]李雨健.六軸碼垛機器人的軌跡規劃與關節摩擦補償研究[D].哈爾濱：哈爾濱工業大學，2017.

[4]吳曉敏，劉暾東，賀苗，高鳳強，邵桂芳.機器人關節摩擦建模與補償研究[J].儀器儀表學報，2018，39（10）：44-50.

[5]K.Johanastrom，C.Canudas-de-Wit.RevisitingtheLuGrefrictionmodel[J].IEEEControlSystemsMagazine，2008，28：101-114.

[6]D.Kostic，BramdeJager，M.Steinbuch，etal.Modelingandidentificationforhigh-performancerobotcontrol：anRRR-roboticarmcasestudy[J].IEEETransactionsonControlSystemsTechnology，2004，12：904-919.

[7]B.Armstrong，O.Khatib，J.Burdick.TheexplicitdynamicmodelandinertialparametersofthePUMA560arm[J].IEEEInternationalConferenceonRoboticsandAutomation，1986，3：510-518..

[8]HaoLei，PaganiRoberto，BeschiManuel，etal.DynamicandFrictionParametersofanIndustrialRobot：Identification，ComparisonandRepetitivenessAnalysis[J].Robotics，2021，10（1）：49.

[9]MadsenEmil，RosenlundOlufSkov，BrandtDavid，etal.AdaptivefeedforwardcontrolofacollaborativeindustrialrobotmanipulatorusinganovelextensionoftheGeneralizedMaxwell-Slipfrictionmodel[J].MechanismandMachineTheory，2021，155：104-109.

[10]W.He，A.O.David，Z.Yin，etal.NeuralNetworkControlofaRoboticManipulatorWithInputDeadzoneandOutputConstraint[J].IEEETransactionsonSystems，Man，andCybernetics：Systems，2016，46：759-770.

[11]李敏，王家序，肖科，等.基于模糊RBF神經網絡動態摩擦分塊補償的機器人數字魯棒滑?？刂扑惴╗J].中國機械工程，2012，23（23）：2792-2796.

[12]賀苗，吳曉敏，邵桂芳，等.基于RBFNN的機器人關節摩擦建模與補償研究[J].儀器儀表學報，2020，41（11）：278-284.

[13]張競.工業機器人關節摩擦補償策略研究[D].廈門：廈門大學，2019.

[14]ShuzhiS.Ge，C.C.Hang，L.C.Woon.Adaptiveneuralnetworkcontrolofrobotmanipulatorsintaskspace[J].IEEETransactionsonIndustrialElectronics，1997，44：746-752.

3299500338258