如何破解極值點偏移問題

黃小妹

(廣西南寧市第三中學 530201)

破解極值點偏移問題需要扎實掌握相關的理論.教學中應結合具體的圖像為學生講解極值點偏移的情境以及存在的不等關系，在其頭腦中留下深刻的印象.同時，認真總結與匯總歷年高考中有關極值點偏移的習題題型，在課堂上為學生逐一的剖析、講解，使其掌握不同題型的解題思路，給其以后解答類似問題帶來良好啟發.

一、不含參數極值點偏移的處理

不含參數極致點偏移問題常作為某一壓軸題的其中一小問，考查學生對導數知識的靈活應用情況.解答該類習題的方法多種多樣，其中構造一元函數是常用的解題思路.解題時應靈活運用導數知識研究給出的已知函數圖像，對其增減、極值情況進行大致判別.而后注重應用題干中給出的已知條件通過等量代換將多元變量轉化為一元變量，構造對應的函數.以構造的函數為研究對象，通過二次應用導數知識找到其中的不等關系完成解答.

例1已知函數f(x)=xe-x(x∈R)，若x1≠x2，且f(x1)=f(x2)，證明：x1+x2>2.

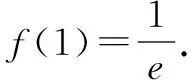
二、含有參數極值點偏移的處理

含有參數的極值點偏移問題難度又提升了一個檔次.眾所周知，一般的極值點偏移問題涉及兩個變量，但含有參數后出現三個變量.很多學生遇到該類題目不知如何下手.事實上，解答該類問題應結合經驗，先通過化歸消去參數，化陌生為熟悉，再進行求解.該題目對學生的解題經驗具有一定要求，因此，教學中應注重多組織學生進行該類習題的訓練，使其積累豐富的經驗.

例2已知函數f(x)=ex-ax的兩個零點分別為x1、x2，且x12.

ex1=ax1

①

ex2=ax2

②

三、含對數式極值點偏移的處理

解答該題目時根據已知條件構建等式關系進行巧妙的轉化是關鍵.根據函數表達式可知x>0，顯然x1x2>0.

又因為函數與直線交于兩點，則可得x1lnx1=m，x2lnx2=m，

①

②

則①-②得：

兩邊同除以lnx1-lnx2，

③

①+②整理得到：

④

由對數均值不等式

對函數f(x)=xlnx求導得到：

f′(x)=lnx+1，x>0，

圖1

極值點偏移是高中數學導數部分的重點、難點，是高考的熱門考點.教學中為使學生掌握相關題型的解題方法，不斷提高學生的解題能力，既要與學生一起推導相關的結論，做好解題理論的講解，又要對相關習題分門別類，為學生做好解題示范，使學生掌握相關題型的解題規律，以后遇到類似問題能夠少走彎路，迅速破題.