中職“直線與圓錐曲線”專題解題分析

李士榮

(江蘇省吳江中等專業學校 215200)

直線與圓錐曲線類題型，是一種兼具對學生基礎考察和能力檢測的題型.當此類題型出現在選擇、填空及解答題型中時，往往是出于學生對圓錐曲線的定義、標準方程等基礎知識點的考察，只要學生們按部就班、仔細研判，通常不難得到正確答案.而當此類題型出現在解答題中，往往會與圓錐曲線的軌跡、位置、弦長、最值等相關聯，需要學生能夠融合函數、方程、幾何等知識點，并對數形結合、空間想象及復雜類計算等能力實施考察.

一、直線與圓錐曲線的基礎性質類題型

對于直線與圓錐曲線基礎性質類問題，其往往是考察一個圓錐曲線與一條或多條直線之間的組合關系，又或者是與其它平面圖形相聯系，對學生關于圓錐曲線知識點的掌握進行全面考察.結合長期的教學經驗，針對此類基礎類題型，可以通過采用待定系數法的方式，從而實現快速求解.

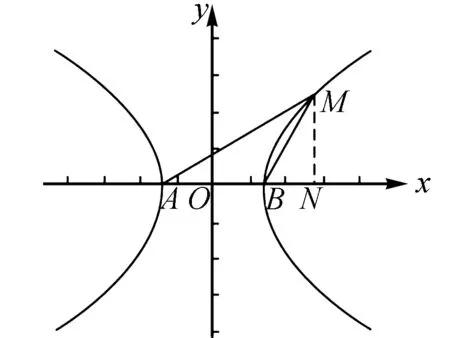
圖1

例1 已知雙曲線的兩個定點分別為A、B，且點M為雙曲線上的任意一點，其中點A、B、M組成的△ABM為等腰三角形，其鈍角為120°，求雙曲線的離心率.

分析結合題中已知條件可知，欲求解本題，等腰三角形是最重要的條件.不妨使用待定系數法，假設雙曲線方程，利用等腰性質實現求解.

二、直線與圓錐曲線的位置關系類題型

求解直線與圓錐曲線的位置關系時，待定系數法往往是最直接的方法，通過假設直線方程為Ax+By+C=0(A，B不同時為0)，利用待定系數的方法，將其代入圓錐曲線的表達式，此時，利用消元法消去其中一個未知數，得到關于另外一個未知數的方程，再分類討論a≠0及a=0的情況下，便可實現判斷.

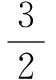
分析針對此題，可以利用待定系數法假設直線l的方程，再與拋物線聯立方程組消元求解，并結合交點個數，求解直線方程.

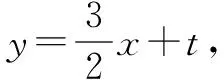
三、直線與圓錐曲線的弦長類問題

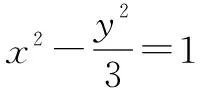
分析本題雖說包含直線、雙曲線和拋物線，并存在交點、中點等，但若是利用點差法，假設處各個點的坐標，聯立方程組，并結合已知條件，便可實現順利求解.

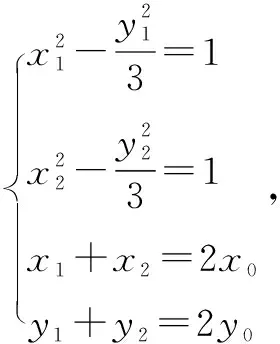
四、直線與圓錐曲線的最值類問題

圓錐曲線最值問題的題型眾多，但最終的求解方法無異于兩類.一是幾何求解方法，即是利用圓錐曲線的定義、性質及定理等實施求解；二是利用代數的方法進行求解，即是將最值求解的幾何量或表達式轉化成函數或不等式的形式進行求解.

分析針對該四邊形面積的最值求解，其最大值較為明顯，即是當其中一條直線經過通徑時，故本題的難點就在于判斷何時四邊形面積取得最小值.其核心方法就是建立關于面積變量的目標函數.

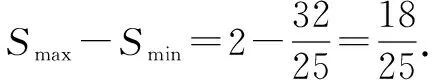
總之，對于直線與圓錐曲線的試題類型眾多，解題方法也是千變萬化.但無論如何，其基本考點無非是對圓錐曲線的概念、性質、交點及軌跡等，有效求解方法無非是待定系數、點差法等.相對重點題型的一對一訓練，更重要的還是從題干入手，結合各題的已知條件及類型，找出針對性的求解方法，實現對癥下藥，從而快捷高效求解.