磨粒半徑對金剛石研磨加工影響機制的仿真研究*

張桐齊, 岳曉斌, 雷大江, 楊 寧

(中國工程物理研究院 機械制造工藝研究所, 四川 綿陽 621000)

金剛石材料有著極高的硬度和耐磨性，在民用和軍事領域有著無可替代的應用價值。截至目前，加工金剛石最有效的方法是金剛石磨粒機械研磨法，其中金剛石磨粒粒徑對金剛石被研磨表面質量有著重要影響。金剛石研磨的經驗表明[1-3]：金剛石磨粒粒徑越小，金剛石工件表面的加工質量越優，但磨粒粒徑對金剛石工件表面質量的具體影響機制尚不明晰，困難在于現有的試驗和檢測技術手段無法直接觀測納尺度下的金剛石研磨加工動態行為。然而，通過分子動力學仿真手段可以較好地研究這一細微過程，獲得試驗難以測量的物理量變化規律，從而解析磨粒粒徑對金剛石加工質量的影響機制，有助于將研磨工藝的經驗性認識轉化為科學性認識，進而為獲得高質量的金剛石加工表面提供理論支撐。

分子動力學(MD)仿真能在原子尺度研究材料的相變、遷移、力學等行為，被廣泛用于研究納尺度加工過程中材料的去除過程[4]。PASTEWKA等[5]采用MD仿真對金剛石不同晶面間的對磨進行模擬，首次從原子層面解釋了金剛石去除率的各向異性特點；李增強等[6]采用MD仿真研究了金剛石刀具研磨的材料去除過程，發現材料在刻劃過程中存在晶格相變和亞表面損傷，仿真結果與XPS檢測結果吻合；YANG等[7]采用MD研究獲得了非晶層的層次結構，并解釋了金剛石機械研磨中晶態碳原子非晶化轉變的主要形式；ZONG等[8]研究了金剛石研磨去除率各向異性的成因，發現材料去除速率在很大程度上取決于sp2雜化與無定形sp3雜化的比例，其比例在新生成的表面層和碎片中越大，拋光的材料去除率越高；SHI等[9]用MD方法研究了載荷和轉速對金剛石研磨過程中的界面摩擦特性的影響，發現摩擦力和摩擦系數隨載荷增大而增大，隨轉速增大而減小。

上述研究者對金剛石機械研磨的研究主要集中于金剛石材料的去除率、碳原子的非晶化和表層損傷等方面，均未涉及磨粒尺寸對加工表面質量影響的情況。一般情況下，磨粒粒徑是顯著影響金剛石被研磨表面質量的重要因素。因此，采用MD仿真方法模擬不同半徑下的金剛石磨粒對金剛石工件的研磨過程，從力、應力、相變和表面硬度等方面具體揭示磨粒尺寸對金剛石被研磨表面質量的影響。

1 仿真模型建立

1.1 模型的構建

金剛石的研磨過程本質是金剛石磨粒和金剛石工件之間的同質對研。基于此，建立圖1所示的模型。圖1中：工件尺寸為40a×20a×10a(a=3.57 ? =0.357 nm，為金剛石晶格常數)的金剛石理想晶體，被分成邊界層、恒溫層和牛頓層3個區域。其中：邊界層起固定作用，防止工件整體剛性移動；恒溫層的作用是保證切削加工過程中產生的熱量能夠及時向外傳遞，其平均溫度被設置在室溫293 K；牛頓層是研磨過程中材料相變和被去除的區域，且牛頓層原子和恒溫層原子的運動都遵從牛頓第二定律[10]。金剛石磨粒的半徑r選擇6a、10a、15a和20a，即分別為2.142、3.570、5.355和7.140 nm。由于研磨過程中磨粒會在工件表面刻劃出納米溝槽，將磨粒設置為剛體[11]。

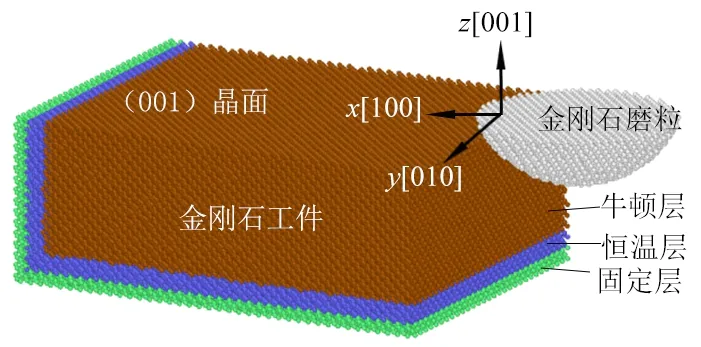
圖1 磨粒研磨工件的分子動力學模型Fig. 1 MD model of abrasive grinding workpiece

工件模型具有x、y、z坐標方向上的[100]、[010]、[001] 3個晶向，磨粒沿[100]晶向對工件(001)面進行刻劃。仿真中，y軸方向采用周期性邊界來減小模型尺寸對仿真結果的影響，x和z方向設為自由邊界條件。根據文獻[12]，仿真時間步長取0.5 fs。

1.2 勢函數選取及力和應力的計算

由于磨粒和工件都是金剛石結構，屬于共價鍵結合的材料，因此采用Tersoff勢函數[13]來描述工件原子間、磨粒與工件原子間的相互作用，其表達式為：

(1)

Vij=fC(rij)[fR(rij)+bijfA(rij)]

(2)

其中：E和Ei分別為系統總勢能和原子i的勢能，Vij、rij分別為原子i、j間的勢函數和間距，fR、fA和fC分別為排斥項、吸引項和截斷項函數，bij為低價函數。

勢函數確定后，原子間作用力Fij通過原子間勢函數對間距求導得出：

Fij=-dVij/drij

(3)

作用在第i個原子上的力Fi等于其周圍所有原子對其作用的力的合力：

(4)

與宏觀尺度下使用的連續介質應力不同，微觀尺度的應力計算常用維里應力計算方法[14]：

(5)

其中：σαβ為原子i的維里應力張量；α、β為笛卡爾坐標分量；Ω為截斷域體積；mi、viα和viβ為原子i質量、速度分量。

MD模擬參數如表1所示。仿真計算利用Lammps分子動力學程序[15]完成。

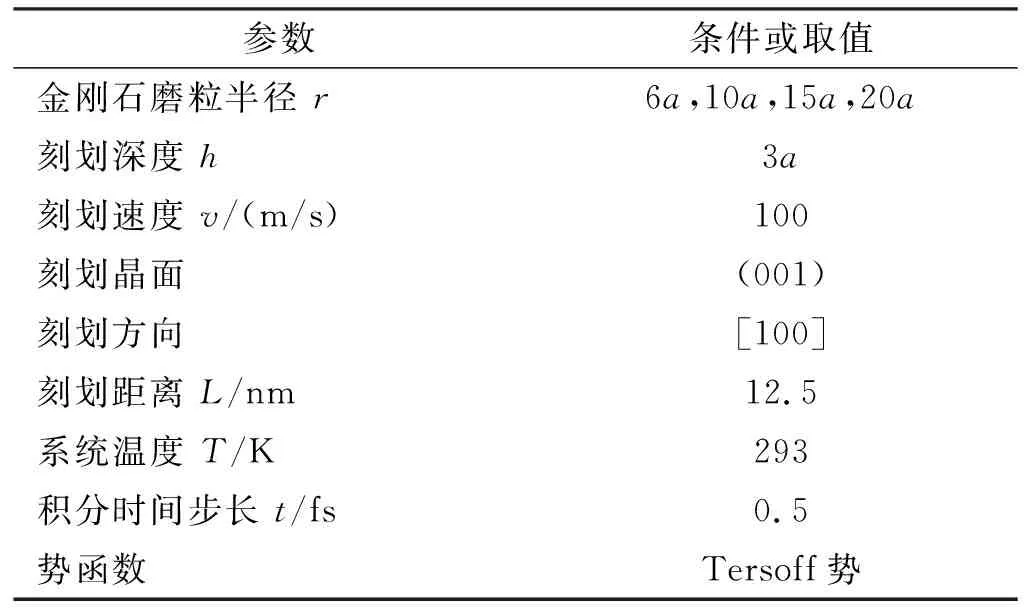
表1 分子動力學模擬參數

2 模擬結果與討論

2.1 研磨過程的力分析

在研磨過程中，磨削力是解釋加工現象的重要物理量。研磨過程中的力主要來源于工件原子和磨粒原子之間的相互作用。在表1條件下，通過對原子每一時刻的位移進行標定，可得式(4)的原子所受的合力，從而得到切向力和法向力的變化曲線，如圖2所示。

圖2的結果表明：磨粒剛接觸工件時，隨著接觸原子增多，磨粒的切向力和法向力快速增大；磨粒移動距離達到9 nm時，其與工件的接觸面積趨于穩定，其切向力和法向力圍繞某恒定值對稱波動。據朱宗孝等[16]對單晶鎳的研究，這種波動是材料位錯形成和運動導致的，這表明研磨過程中金剛石工件表面存在位錯的形成和運動。

對于不同半徑的磨粒，分別提取其穩定切削時的平均切向力和平均法向力，結果如圖3所示。

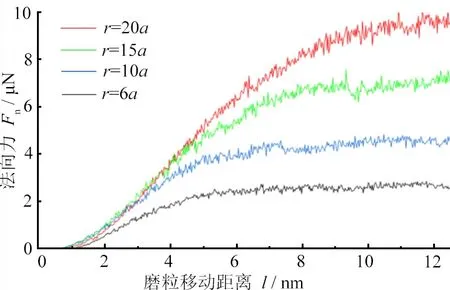
(a)不同磨粒半徑下的的法向力Normal forces under different abrasive radius

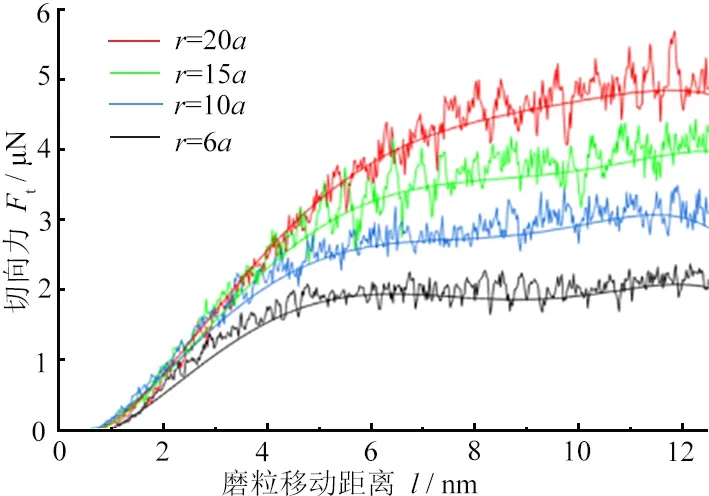
(b)不同磨粒半徑下的切向力Tangential forces under different abrasive radius圖2 磨削過程中的法向力和切向力Fig. 2 Normal & tangential forces in grinding process

圖3 磨粒半徑對平均切向力和平均法向力的影響Fig. 3 Influences of abrasive radius on average tangential force and average normal forces

從圖3可以看到：隨著磨粒半徑r增大，磨削平均切向力和平均法向力呈線性增加；r從6a增加到20a，平均法向力增加了8.8 μN，而平均切向力增加了2.9 μN，平均法向力增量約為平均切向力增量的3倍。由此可知：隨著磨粒半徑增大，磨粒與工件間的剪切作用相對擠壓和摩擦的作用越來越小；同時，隨著磨料粒徑增大，磨削力變化幅度也線性增大，反映出位錯的形成和運動更劇烈，工件亞表面質量變差。

2.2 研磨過程的應力和相變分析

應力和相變是材料被去除時產生的對材料性能有直接影響的因素。通過式(5)計算維里應力，獲得每個原子的維里應力張量σxx、σyy、σzz、σxy、σxz、σyz，進而得出靜水應力[14]:

σhydro=(σxx+σyy+σzz)/3

(6)

圖4為工件的靜水應力分布和相變。圖4a中的原子根據其靜水應力大小進行著色，其中正值代表拉應力，負值代表壓應力。同時，利用共近鄰原子分析技術可以有效辨別金剛石結構和非金剛石結構，進而識別加工過程中的相變[17]。圖4b中的藍色為完好晶格原子區，綠或淺綠色為過渡原子區，白色為非晶相變原子區。

(a)研磨區域應力圖Grinding area stress diagram (b)研磨過程相變圖Phase transformation diagram of grinding process圖4 工件的靜水應力分布和相變Fig. 4 Hydrostatic stress distribution and phase transformation of workpiece

結合圖4a、圖4b的對應區域可以看出：磨粒前下方由磨粒推擠形成高壓應力區A1，金剛石晶格被這種壓應力徹底破壞；而拉應力集中在磨粒劃過的A2區域，由磨粒“后刀面”與工件間的摩擦造成。由于仿真的區域是固定的，故A1和A2區域也相對固定，以后的仿真研究都在此區域進行，區域的位置都與圖4a標示的相同。

不同磨粒半徑下的靜水應力分布如圖5所示。由圖4和圖5可知：隨著磨粒半徑增大，壓應力影響區A1顯著增大，拉應力影響區A2也有所增大。

為了更加準確地分析應力影響區，分別統計A1區域壓應力數值大于150 GPa的總原子個數n1，A1區內受剪切和受擠壓的原子個數n2和n3(n1=n2+n3)及其所占比例，A2區域拉應力大于30 GPa的原子個數n4，結果如表2所示。表2中：隨磨粒半徑從6a增加到20a，A1高壓相變區受剪切作用的原子數占相變原子總數的比例由57.02%降低到15.02%，受垂直擠壓的原子數比例則從42.98%增加至84.98%。同時，加工表面A2區域拉應力大于30 GPa的原子數也隨磨粒半徑增加有所增加，這與垂直壓力增大引起的摩擦力增大相一致，而表面拉應力的增大會使工件表面質量變差。

(a)半徑6a Radius 6a(b)半徑10a Radius 10a(c)半徑15a Radius 15a(d)半徑20a Radius 20a圖5 不同磨粒半徑下的磨削區靜水應力分布Fig. 5 Distribution of hydrostatic stress in grinding zone under different abrasive grain radii

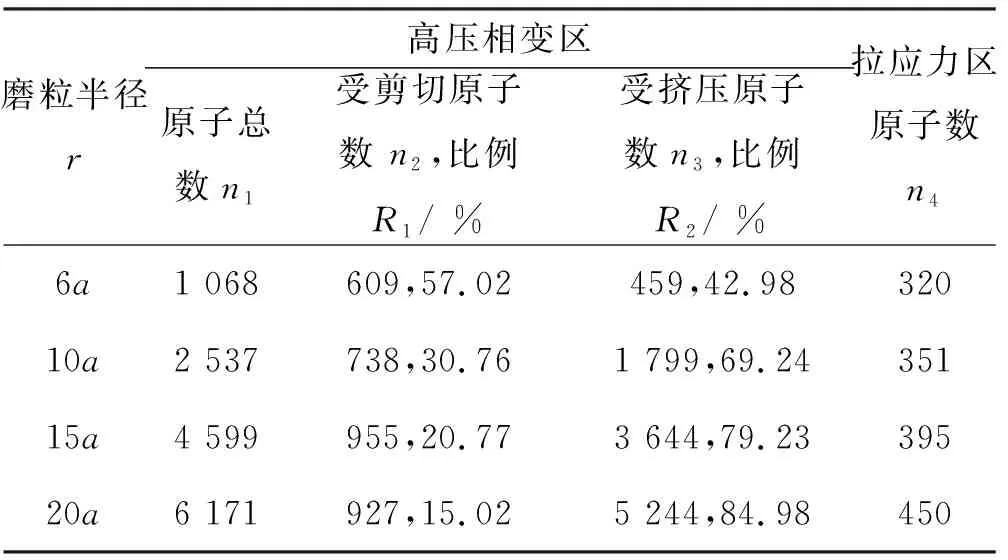
表2 高壓相變區原子和拉應力區原子分布

圖6為不同磨粒半徑下的磨削區相變分布。如圖6所示：磨粒半徑愈大，非晶相變區域愈大，與應力分布的分析一致。由于A1壓應力區原子數增加使相變深度增加，且磨粒半徑愈大，研磨區后方殘留下的缺陷愈多，與A2拉應力區的原子數量增加相一致。

2.3 磨粒半徑對加工表面硬度的影響

金剛石工件表面的顯微硬度是表征其加工質量的重要指標，其值可由納米壓入模擬試驗獲得。采用半徑為6a的剛性球形金剛石壓頭，在未研磨或研磨后的區域豎直壓入工件，壓入速度為10 m/s，納米壓入示意圖如圖7所示。

(a)半徑6a Radius 6a(b)半徑10a Radius 10a(c)半徑15a Radius 15a(d)半徑20a Radius 20a圖6 不同磨粒半徑下的磨削區相變分布Fig. 6 Phase change distribution in grinding area under different abrasive grain radii

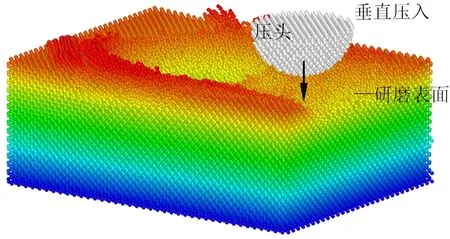
圖7 納米壓入示意圖Fig. 7 Schematic diagram of nanoindentation

壓入載荷隨壓入深度變化的曲線如圖8所示。由圖8可以看出：研磨后金剛石表面的承載能力明顯比未研磨的金剛石表面承載能力小，且磨粒越大承載能力越差，說明研磨后工件表面的硬度下降，且磨粒越大表面硬度下降越嚴重。為了更好地進行說明，進一步計算工件的顯微硬度。

工件顯微硬度值Hv可由壓入載荷G和壓痕投影面積B的比值求出，即Hv=G/B[18]。由于納米壓頭形狀是球形，不考慮其他因素的影響，則壓痕的投影可近似地等效為圓形，其面積B與壓頭壓入深度H的關系可表示為B=πH×(2R-H)，其中R為球形壓頭的半徑。顯微硬度隨壓入深度的變化如圖9所示。

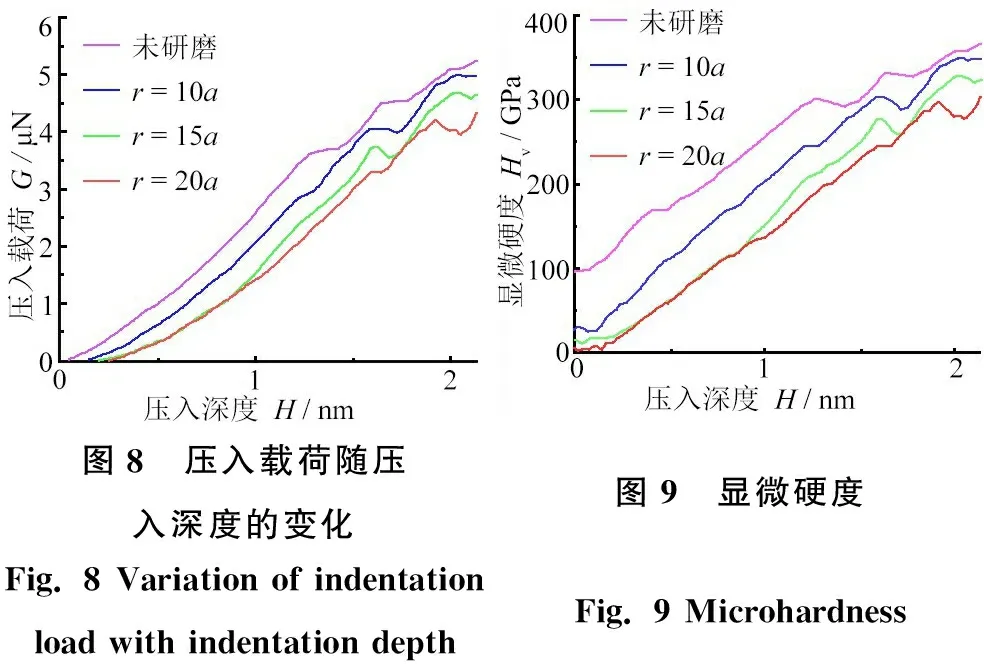
圖8 壓入載荷隨壓入深度的變化圖9 顯微硬度Fig. 8 Variation of indentation load with indentation depthFig. 9 Microhardness

圖9表明：計算所得的工件顯微硬度并不是一個恒定值，而是隨著壓入深度增大而增大，表現出顯著的尺寸效應。當壓入深度為2 nm時，未研磨的表面硬度為355 GPa，半徑為10a、15a和20a的磨粒刻劃工件表面的顯微硬度分別為345、321 和290 GPa,分別比未研磨表面降低了2.8%、9.6%、18.3%。即磨粒半徑從20a減小到10a，可將加工表面的顯微硬度減小程度降低約1/6。

3 結論

通過模擬相同磨削深度和磨削速度下，不同半徑的剛性金剛石磨粒對金剛石工件的刻劃過程，得到如下結論:

(1)隨著磨粒半徑增大，磨削平均切向力和平均法向力呈線性增加；磨粒半徑從6a增加到20a，平均法向力增加了8.8 μN，而平均切向力增加了2.9 μN，平均法向力增量約為平均切向力的3倍。且研磨過程存在磨削力波動，磨粒愈大，磨削力波動幅值愈大，表明工件表面的位錯形成和運動更劇烈。

(2)磨粒前下方形成強壓應力區，工件晶格被壓應力破壞，磨粒后方有摩擦造成的集中拉應力區；磨粒半徑從6a增加到20a，高壓相變區受剪切作用的原子數占相變原子總數的比例由57.02%降低到15.02%，而受垂直擠壓的原子數比例從42.98%增加至84.98%。

(3)磨粒半徑愈大，非晶相變區域愈大，垂直擠壓導致的摩擦力增大使磨粒后方拉應力區愈大，磨粒后方殘留下的缺陷愈多。

(4)通過納米壓入模擬試驗得到工件的表面顯微硬度，其值隨著壓入深度增大而增大；當壓入深度為2 nm時，半徑為10a、15a和20a的磨粒刻劃后的工件表面顯微硬度與未刻劃表面的比有所降低，其值分別降低了2.8%、9.6%和18.3%，磨粒半徑從20a減小到10a，可將加工表面的顯微硬度減小程度降低約1/6。