顧及時變非高斯噪聲的高斯和濾波及其導航應用

戴 卿 馮 威 許輝熙

1 西南交通大學地球科學與環境工程學院，成都市二環路北一段111號，610031 2 四川建筑職業技術學院博士后創新實踐基地，四川省德陽市嘉陵江西路4號，618000

擴展卡爾曼濾波是高斯白噪聲假設條件下常見的非線性濾波算法，已在導航定位、目標跟蹤和制導控制等領域得到廣泛運用[1]。當高斯白噪聲假設條件不符時會發生濾波精度下降的現象，為此許多學者提出基于模型補償算法的自適應濾波理論，主要有Sage-Husa濾波、漸消濾波、抗差自適應濾波等[2-3]，這些濾波方法在處理非高斯噪聲污染問題時，真實噪聲模型往往通過具有更大方差的高斯分布來涵蓋。近年來，一種源于高斯混合模型(Gaussian mixture model, GMM)的多模近似方法為解決非高斯噪聲問題提供了另一可行途徑，比采用膨大方差的高斯分布近似法具有更高精度[4-7]，在一定程度上可解決非線性非高斯模型的狀態估計問題。但GMM建模參數不能隨非高斯噪聲統計特性的變化而變化，這種局限性使得高斯和濾波不能有效應對非高斯噪聲的時變性。

本文在分析GMM分解特性的基礎上研究高斯分量間位移參數對高斯和擴展卡爾曼濾波(Gaussian sum extend Kalman filter，GSEKF)擬合精度的影響，通過參數自適應技術獲取最優位移參數，并對GMM進行實時修正，從而提升時變非高斯噪聲環境下GSEKF的估計精度和穩定性。實驗結果表明，本文探討的參數自適應GSEKF算法在處理時變非高斯噪聲問題上具有可行性。

1 問題描述

GNSS/SINS緊組合定姿定位系統具有較好的導航精度和抗干擾能力，在處于大失準角和高機動狀況時，傳統線性化模型會降低解算精度，需建立非線性數學模型[8]。設k時刻狀態向量Xk為包含姿態、速度、位置、陀螺漂移、加速度計漂移、GNSS時鐘偏置和時鐘漂移的18維列向量，其中姿態可用四元數表示，狀態方程可概括為：

Xk=f(Xk-1)+GkWk

(1)

式中，f(·)為非線性函數，Gk為噪聲系數陣，Wk為過程噪聲，具體設置見文獻[1]。

GNSS觀測數據經衛星鐘差、電離層延遲和對流層延遲改正后，整理得到量測方程為：

Lk=h(Xk)+vk

(2)

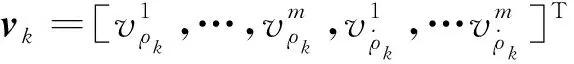
文獻[9-10]對GNSS噪聲殘余項進行Allan方差分析，發現其與零均值高斯白噪聲的特性不符，為非高斯與高斯的混合分布，且由于受到外界因素影響，具有一定時變性。因此，為改進組合導航定姿定位性能，需在濾波計算中顧及非高斯時變噪聲的影響。

1.1 GMM建模

在非高斯環境下，利用GMM將式(2)中量測噪聲分布模型近似為2個高斯分量的形式[7]：

p(v)≈εN(vA;μA,ΣA)+(1-ε)N(vB;μB,ΣB)

(3)

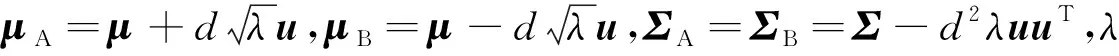
1.2 GMM局限性分析

非高斯噪聲通過GMM分解可得到其分布模型的近似形式，然而現實導航測量環境具有動態性和復雜性等特點，故干擾噪聲頻率因子ε也會發生改變。這種不確定性使經典GMM對非高斯噪聲建模存在一定局限性，若直接將其應用于動態導航GSEKF算法中則不能有效應對復雜的時變非高斯噪聲環境，從而會引起濾波隨機模型失配，嚴重時會降低估計精度。

2 位移參數自適應GSEKF算法

2.1 位移參數特性分析

GMM分解過程中位移參數d可限定2個不同高斯分量均值之間的距離。由式(3)可知，當d<0.5時，分量(1-ε)N(vB;μB,ΣB)比分量εN(vA;μA,ΣA)弱；當d>0.5時則相反。以往在非高斯噪聲發生變化時，d=0.5的經驗性取值并不具有最優性，若d能隨時跟蹤調整，則算法將具有一定的自適應能力。

圖1為位移參數d與GMM分解過程的關系，紅線p代表真實非高斯噪聲模型，藍線p(A)和p(B)分別代表2個不同的高斯分量。當d<0.5時，GMM實際計算區域為綠線p(1)、p(2)和x軸所包圍的區域，記為M；同理d>0.5時對應區域為N。陰影范圍代表實際GMM對真實非高斯噪聲的近似程度，重合度越高則擬合效果越好。由于非高斯噪聲的時變性會引起干擾噪聲頻率因子ε隨之改變，故當分量(1-ε)N(vB;μB,ΣB)發生強化時，區域M中2個高斯分量的均值會背離零均值方向，此時若使d>0.5，則區域N的濾波效果比區域M更優。

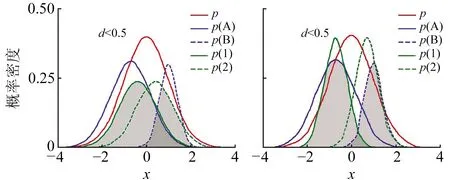
圖1 位移參數d與GMM分解過程關系Fig.1 Relationship between displacement parameter and GMM

由此可見，位移參數d的自適應變化能較好地跟蹤時變非高斯噪聲，使GMM分解過程更合理，對實際非高斯噪聲的擬合也更接近，可獲得更精準的隨機模型，從而改善GSEKF的估計效果。

2.2 算法原理

本文從高斯分解合理性的角度出發，通過代價函數、位移參數和步長來彌補GMM的缺陷，優化算法的自適應能力，設計一種位移參數自適應GSEKF算法，該算法過程可描述為：

1)確定自適應步長l，設位移參數d的變化范圍為[da,db]，令d=da；設代價函數為pg(Lk|Lk-1,d)，最大似然函數為H=0。

(4)

(5)

式中，Φk,k-1為狀態轉移陣，ΣWk為過程噪聲協方差陣。

3)依據式(3)對非高斯量測噪聲進行建模，并將其與EKF算法結合，使原先單個EKF分解為2個平行的EKF子濾波器：

(6)

(7)

(8)

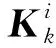
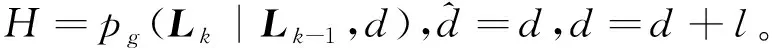
(9)

(10)

(11)

(12)

本文位移參數自適應GSEKF算法流程如圖2所示，通過位移參數d的自適應調節可彌補GMM的缺陷，在理論上具有更理想的估計精度。

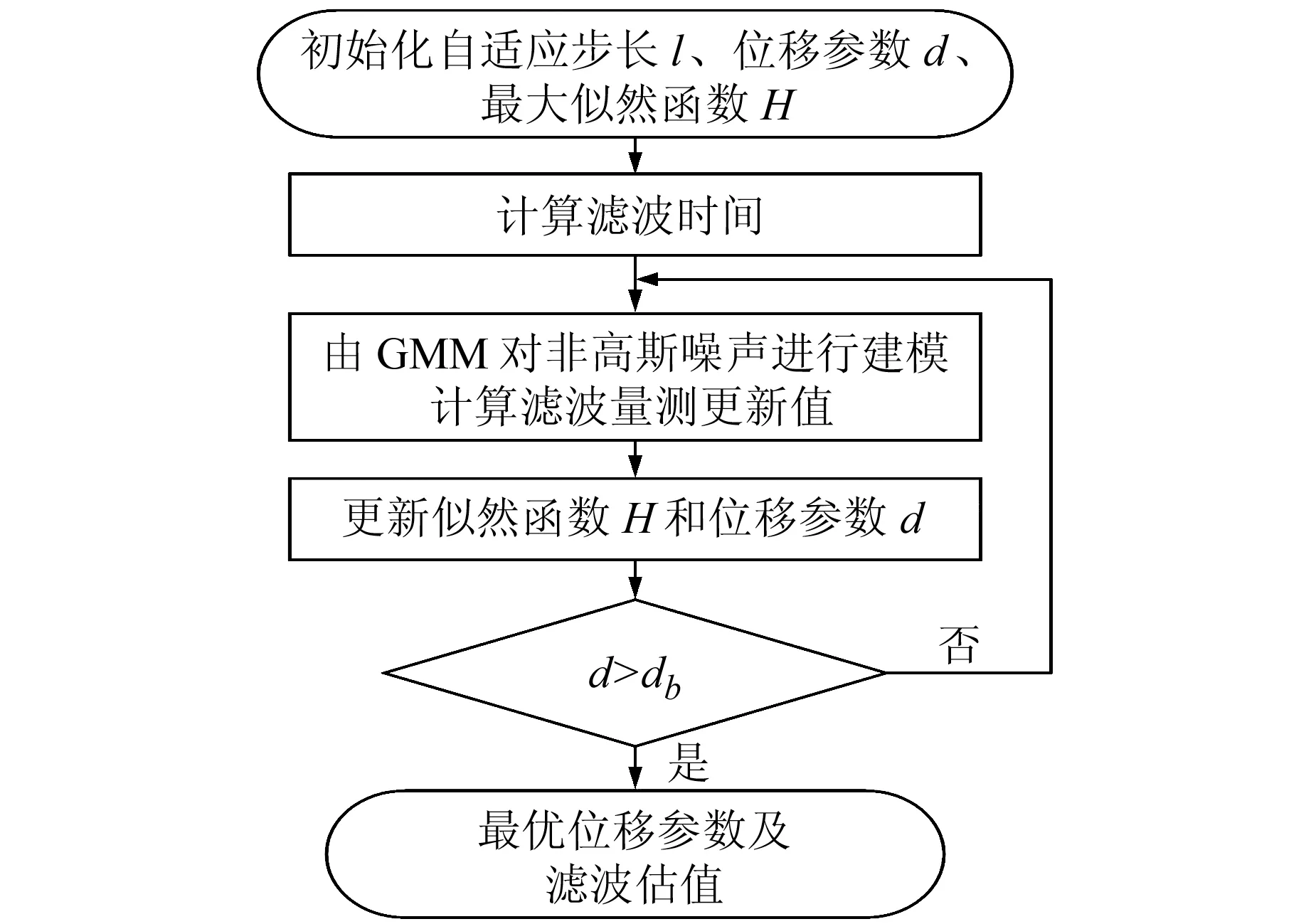
圖2 參數自適應GSEKF算法流程Fig.2 Flow chart of parameter adaptive GSEKF algorithm

3 算例與分析

3.1 仿真檢校

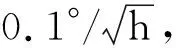
設置ε初值為0.5，并從500 s開始每隔250 s跳變1次，如圖3所示。用2種不同的濾波方案進行數據處理：方案1，GSEKF算法；方案2，位移參數自適應GSEKF算法。計算平臺為Inter Core i7-8550u 1.8GHz，RAM 8GB，計算軟件選用MATLAB R2014a。

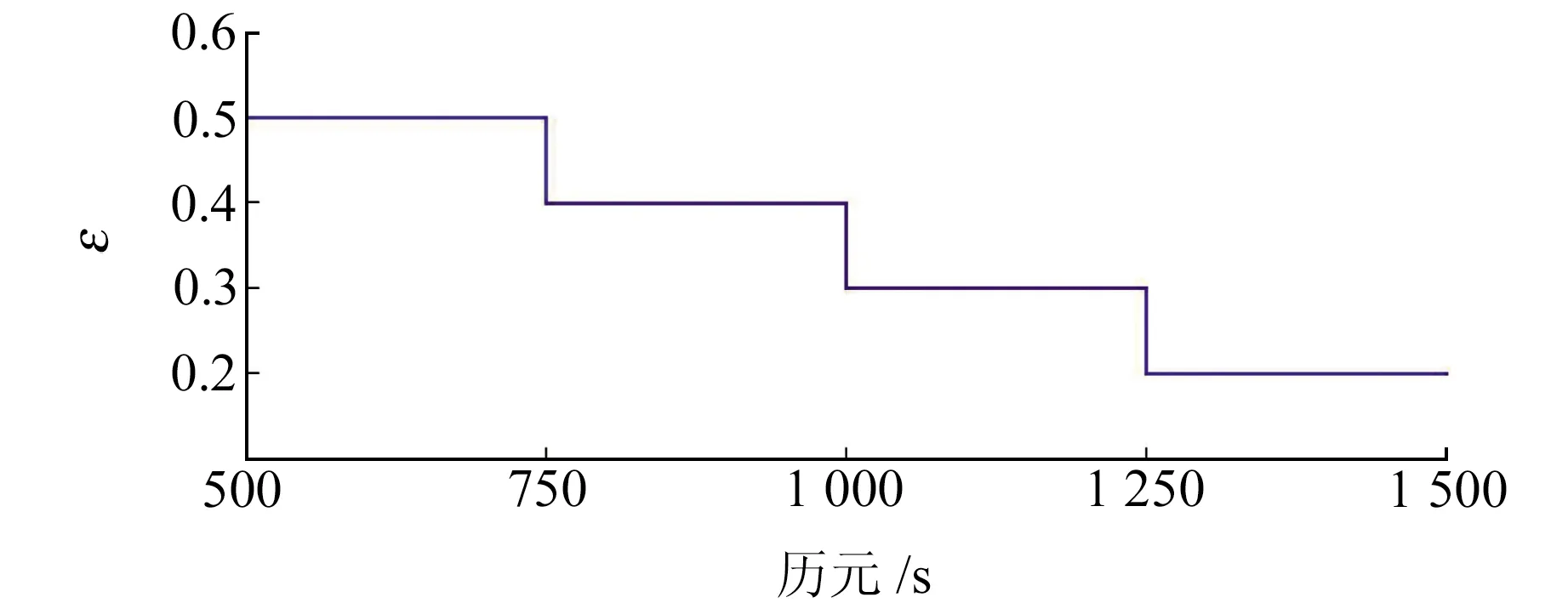
圖3 ε值變化情況Fig.3 The variation of ε

圖4為500～750 s濾波結果，在ε發生跳變前，方案1和方案2的估計結果相近，2個方案非高斯噪聲建模較為準確，因此均能較好收斂。圖5為1 250～1 500 s濾波結果，由于方案1中GNSS量測噪聲GMM建模不準確，導致姿態角估計結果較差，其相應的速度和位置估值也受到影響(多個歷元點處的估值超過3σ誤差界限)；而方案2利用自適應修正的位移參數可較好地跟蹤時變非高斯噪聲，取得比方案1更為穩定的濾波效果。

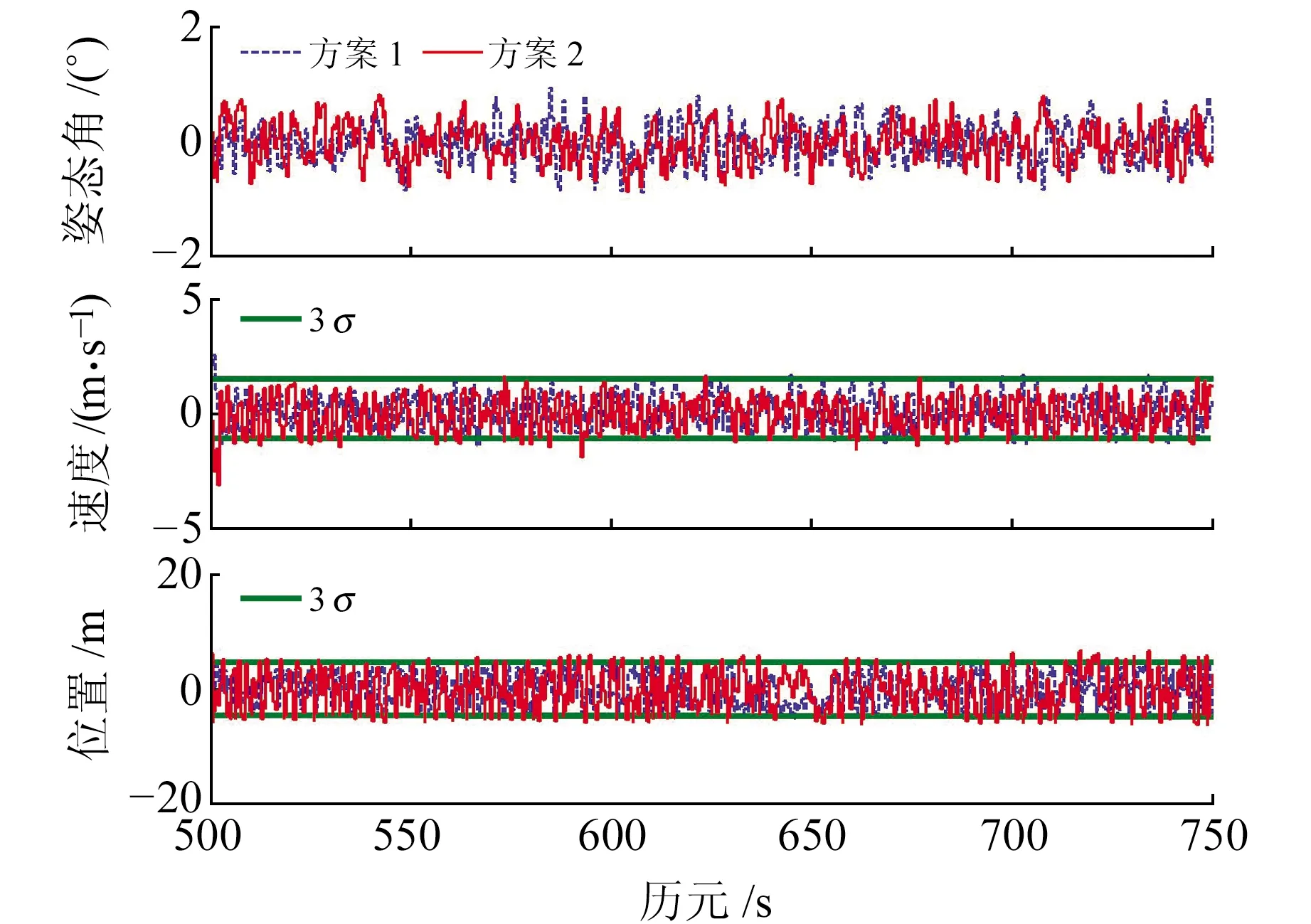
圖4 500～750 s估計誤差曲線Fig.4 Estimation error curve of 500～750 s

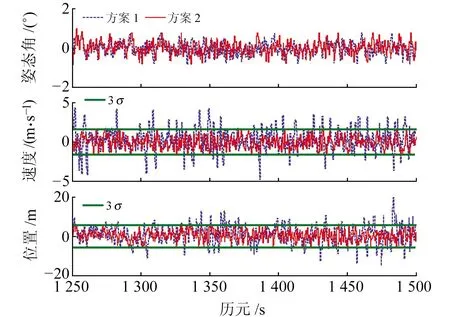
圖5 1 250～1 500 s估計誤差曲線Fig.5 Estimation error curve of 1 250-1 500 s

為體現算法比較的公正性，在相同參數條件下進行50次蒙特卡洛仿真實驗，采用均方根誤差(RMSE)和單位歷元計算耗時進行量化比較。如表1所示，方案1的估計誤差略大，方案2由于對位移參數進行實時修正，使得GSEKF的隨機模型具有自適應性，從而獲得更高的濾波精度。但方案2需要對參數d進行迭代更新，因此耗時比方案1略長。

表1 不同方案RMSE和運算時間比較

為進一步驗證算法的性能，仿真不同歷元數量的數據進行測試，結果如表2所示。由表可知，歷元數增加會使估計精度降低，但方案2始終優于方案1。以姿態估計為例，2 000個歷元時方案2精度較方案1高約13%，4 000個歷元時其精度優勢更為明顯，高約22%。由于姿態角精度會影響定位結果，因此方案2的位置估計精度也高于方案1。由此可見，方案2在復雜的時變非高斯噪聲環境下可表現出較高的濾波精度，且在長航時導航解算中具有更好的濾波穩定性。

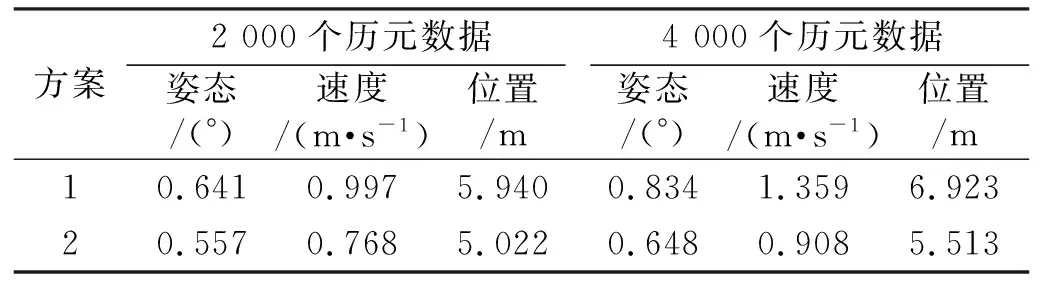
表2 不同歷元長度的濾波結果比較

3.2 實驗測試

實驗數據采集于GNSS/SINS組合導航裝置，其中GNSS接收機可接收GPS和BDS雙系統信號，采樣率為1 Hz，三軸陀螺零偏穩定性小于0.5°/h，采樣率為1 000 Hz。將基于光纖陀螺的GNSS/SINS高精度導航數據作為參考真值，并用于機動載體初始化。機動載體經過建筑物、樹林和水面附近，其運動軌跡如圖6所示，GPS和BDS可見衛星狀況如圖7所示，復雜變化的數據采集環境使得導航噪聲具有時變性和非高斯特性。分別采用§3.1中方案1和方案2進行解算，濾波周期為1 s。

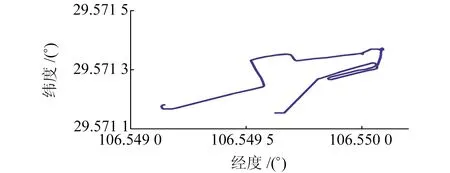
圖6 實驗軌跡Fig.6 Test trajectory

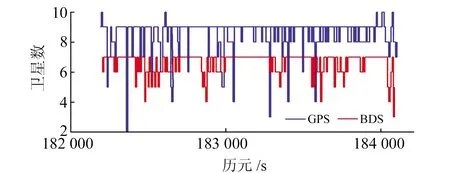
圖7 可見衛星數Fig.7 Number of visible satellites

圖8為其中500個歷元的濾波結果，從圖中可以看出，方案2的濾波精度明顯高于方案1，方案2估計誤差(姿態、速度、位置)的最大值小于方案1。表3為不同方案的量化比較結果，從表中可以看出，方案2優勢明顯，其濾波估計精度比方案1高(姿態提高4%、速度提高5%、位置提高7%)。在單位歷元計算耗時方面，方案2略微增加，但未造成計算效率明顯降低，這是因為位移參數自適應GSEKF算法雖然需要迭代計算位移參數，但可降低GMM的初值敏感性，加快GMM參數估計的收斂速度。由此說明，當機動載體導航環境發生改變時，本文討論的顧及時變非高斯噪聲的高斯和濾波算法能精化隨機模型，進一步提高濾波性能。

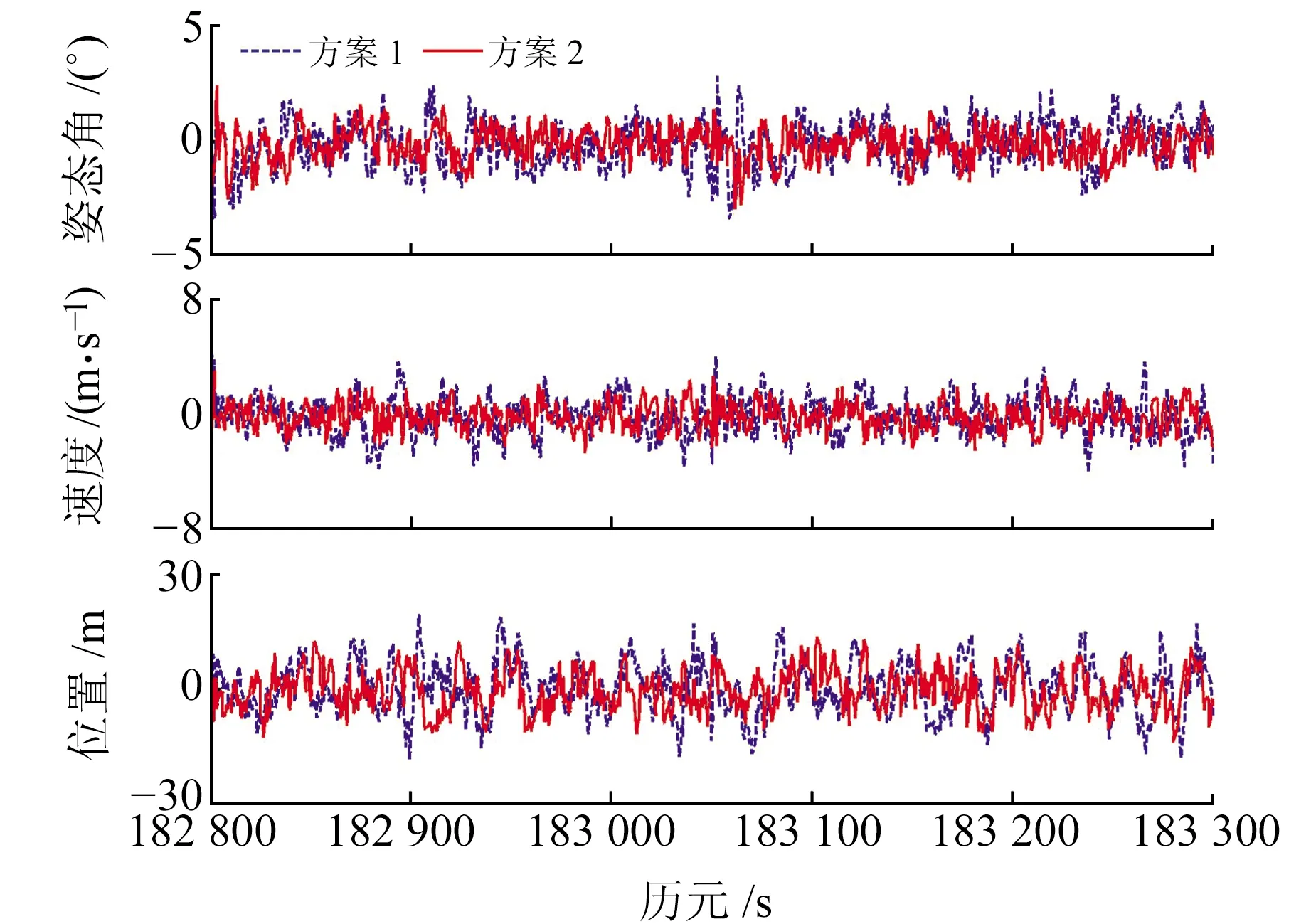
圖8 估計誤差曲線Fig.8 Estimation error curve

表3 不種方案量化比較

4 結 語

針對時變非高斯噪聲下高斯和濾波精度和穩定性下降的問題，設計一種基于位移參數自適應調整的GSEKF算法，該算法可克服傳統GMM的局限性，使GMM分解過程更加合理，可為復雜導航環境下的高精度定姿定位濾波解算提供可能。實驗結果表明，在時變非高斯噪聲導航環境下，本文算法可進一步改善濾波精度和自適應能力，且在長航時導航解算中能表現出更好的穩定性，對非線性非高斯濾波理論及組合導航定姿定位算法研究具有參考意義。