礦區地表沉降監測的一種組合模型預測方法

周文韜 張文君 楊元繼 馬旭東 冉茂瑩

1 西南科技大學環境與資源學院，四川省綿陽市青龍大道中段59號，621010 2 國家遙感中心綿陽科技城分部，四川省綿陽市青龍大道中段59號，621010

礦山地表沉降機理復雜，通常單一預測模型預測數據的精度較低，不能反映礦區地表的真實情況。將單一預測模型進行組合，提取各模型的有效信息來提高預測精度是當前的發展趨勢[1-4]。差分整合移動平均自回歸(autoregressive integrated moving average,ARIMA)模型和Holt-Winters模型都是基于時間序列變化的預測模型，適用于礦山地表沉降時序變化預測。本文基于誘導有序加權平均(IOWA)算子，以SBAS-InSAR監測值作為實際值，將ARIMA模型和Holt-Winters模型進行加權組合，以期為礦山地表沉降監測預測提供新方法。

1 SBAS沉降監測及組合預測模型建立

1.1 SBAS-InSAR技術原理

小基線集(small baseline subset, SBAS)技術可有效改善D-InSAR時空失相干、大氣延遲等缺陷，其原理是將傳統D-InSAR的監測形變結果作為單一觀測值，并根據最小二乘法得到高精度的形變序列[5]。由于實驗研究目標為地表垂向沉降變化，因此本文忽略地表水平位移的影響，將LOS向形變轉至垂向形變。

1.2 基于IOWA算子的ARIMA和Holt-Winters模型的組合預測方法原理

ARIMA模型是針對非平穩時間序列建模的常見模型。ARIMA(p,d,q)稱為差分整合移動平均自回歸模型，其中AR為自回歸項，p為自回歸階數，MA為移動平均項，q為移動平均階數，d為差分階數。ARIMA(p,d,q)模型可表示為：

(1)

式中，L為滯后算子，d∈Z，d>0。當差分階數d=0時，ARIMA模型等同于ARMA模型(即平穩時間序列模型)[6]。本文研究數據均為平穩時序數據，故d均為0。

指數平滑預測法是以具有某種指標的本期監測數據和預測數據為基礎，引入平滑系數，以求取平均數的一種時間序列預測法，其預測公式為：

(2)

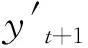
Holt-Winters線性指數平滑法是在上述一次指數平滑的基礎上進行二次指數平滑，其公式為：

(3)

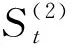
誘導有序加權平均(IOWA)算子是根據有序加權平均(OWA)算子發展而來的新型加權方法，基于IOWA算子的組合預測模型可以有效克服傳統組合預測方法在某個時間點預測精度不同的缺點。IOWA算子原理如下：

假設存在一組監測值xi(i=1,2,…,N),采用m種可行的單預測模型進行預測，第t種方法在時刻i的預測值(或擬合值)為xti(t=1,2,…,m)。設L=(l1,l2,…,lm)為m種單項預測在組合預測中的加權系數，且滿足：

(4)

根據加權算術平均數計算公式，令

(5)

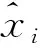
第t種方法在時刻i的預測精度pti可表示為：

(6)

利用m種方法獲得預測值及其預測精度，可構成一個二維數組(p1i,x1i),(p2i,x2i),…,(pmi,xmi)，將pti按從大到小排序，設a-index(ti)是序號為t的預測精度的下標，令

FL((p1i,x1i),(p2i,x2i),…,(pmi,xmi))=

(7)

則式(7)稱為由預測精度序列p1i,p2i,…,pmi所產生的IOWA組合預測值。

從式(7)可以看出，組合預測的賦權系數與單項預測方法無關，而與單項預測方法在各個時間點的預測精度大小密切相關[8]。

令ea-index(ti)=xi-xa-index(ti)，則以誤差平方和為準則的基于IOWA的組合預測最優化模型可表示為：

(8)

2 實驗分析

2.1 研究區概況及數據來源

本文以金昌市龍首礦西二采區為研究區(以下簡稱西二采)。西二采位于我國甘肅省金昌市，其沉降區面積約1.1 km2，如圖1所示，礦區地勢較平坦，平均海拔為1 500～1 800 m。礦區地表水系不發育，常年干枯，屬溫帶大陸性氣候。近年由于地下不斷開采，導致地表塌陷，裂縫明顯，從而對鎳礦資源開采產生極大的安全隱患。

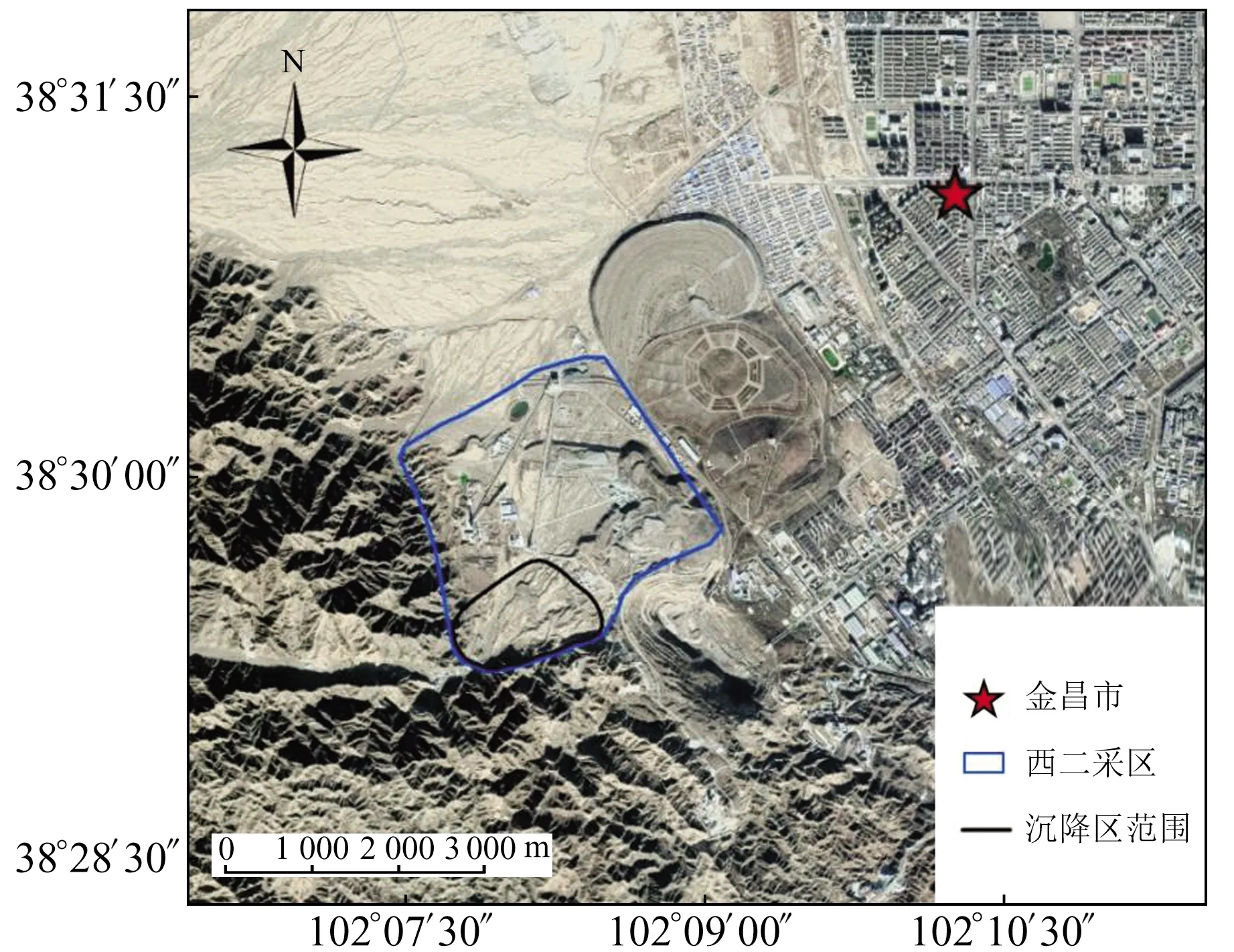
圖1 研究區概況Fig.1 Overview of the study area

選取時間跨度為2019-04-03～2020-01-28的連續26景SAR數據C波段的升軌Sentinel-1A斜距單視復數(SLC)影像，周期為12 d，分辨率為5 m×20 m，實驗參數詳見表1。影像預處理過程中引入AUX_POEORB精密定軌星歷數據，數據處理時選用分辨率為30 m的SRTM DEM數據去除地形相位。

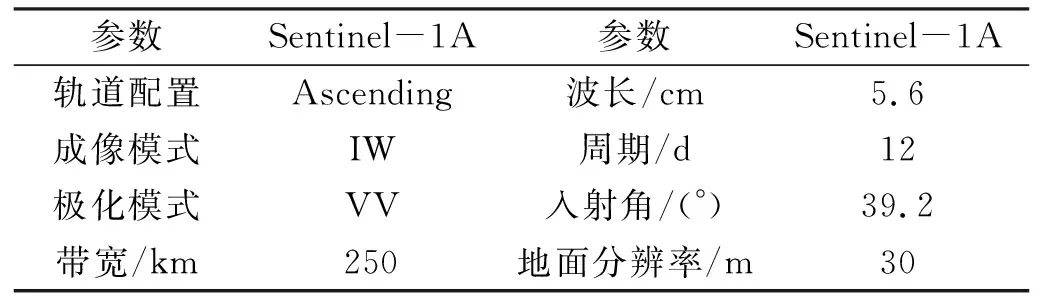
表1 實驗數據參數

2.2 礦區SBAS-InSAR監測及分析

實驗選取覆蓋研究區的26景Sentinel-1A升軌SAR影像，基于SARscape5.2.1版本進行SBAS數據處理。為獲取可靠的形變監測結果，設置臨界基線閾值為2 %，時間基線為150，并引入30 m分辨率的SRTM DEM數據去除地形相位。剔除效果較差的干涉對后，最終選取172個干涉對進行差分干涉處理；設置解纏相干系數閾值為0.2，并選取47個穩定控制點進行軌道精化和重去平；進行形變速率反演和地理編碼，去除大氣相位等誤差影響，得到視線(LOS)向年平均沉降速率和時序累積沉降結果并轉至垂向形變，其中累積垂向沉降值見圖2。

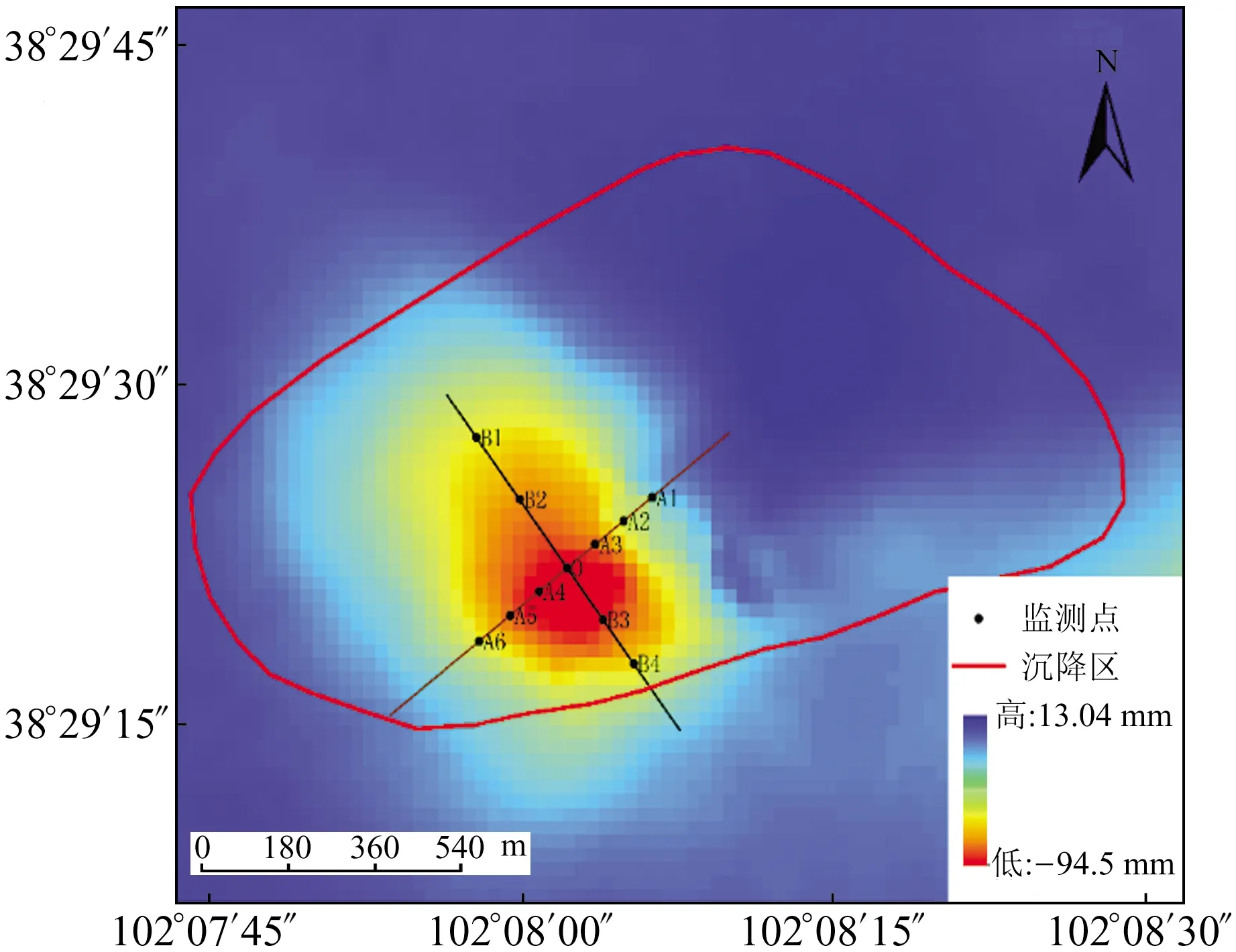
圖2 累積沉降值Fig.2 Cumulative settlement

由圖2可以看出，礦區在監測時段內由地下開采引起的最大累積垂向沉降值達到-94.5mm。為便于后文分析礦區地表沉降預測，將26景影像視為26期時序沉降變化，其中每12 d視為1期，并選取11個監測點進行時序沉降監測分析，包含沿走向分布的6個監測點(A1～A6)、沿傾向分布的4個監測點(B1～B4)及交點O。各點沉降變化曲線如圖3所示，從圖中可以看出，1～4期各監測點呈輕微抬升趨勢；5～12期各監測點呈沉降趨勢，且各點累積沉降值相差較小；12～26期整體沉降速率加快，其中接近沉降中心的A4點累積沉降變化最大，A1點距離沉降中心最遠，累積沉降變化最小。

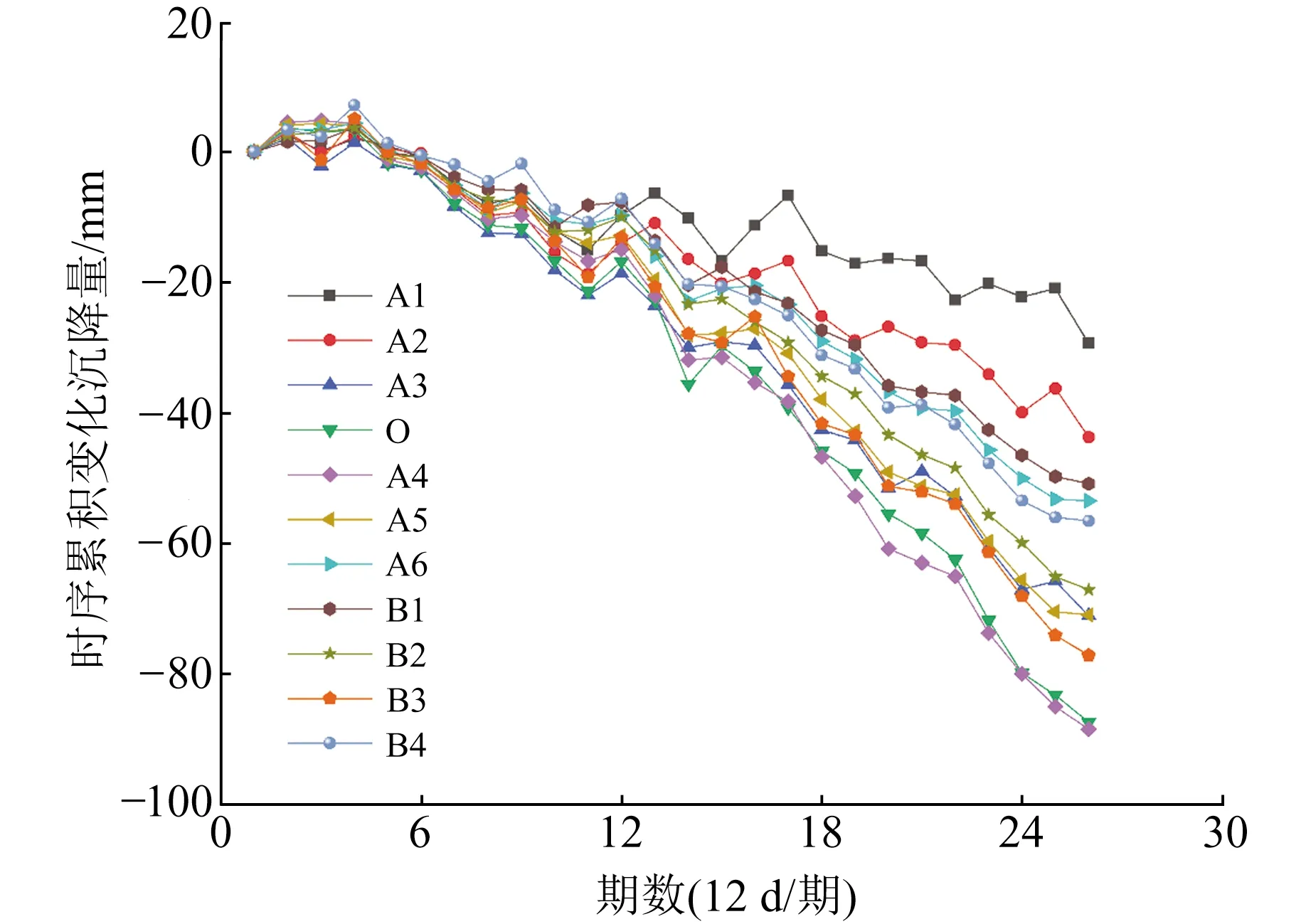
圖3 各點沉降變化曲線Fig.3 Settlement curve of each point

2.3 地表沉降預測及結果分析

由于缺少地面觀測點數據，故將SBAS-InSAR監測數據作為實際值，選取前23期(每期時間間隔為12 d)監測數據對后3期(2020-01-04～28)數據進行預測，并將后3期SBAS監測值與預測值進行對比分析。為證明本文提出的組合預測模型在礦區沉降預測中的可行性，建立3種方案進行分析：方案1采用ARIMA模型進行預測，方案2采用Holt-Winters指數平滑模型進行預測，方案3采用基于IOWA算子的ARIMA和Holt-Winters指數平滑組合模型進行預測。

方案1和方案2采用IBM SPSS Statistics 24.0軟件進行時間序列預測分析，得到各預測模型前23期數據擬合度(表2)、ARIMA模型預測值(表3)和Holt-Winters模型預測值(表4)。

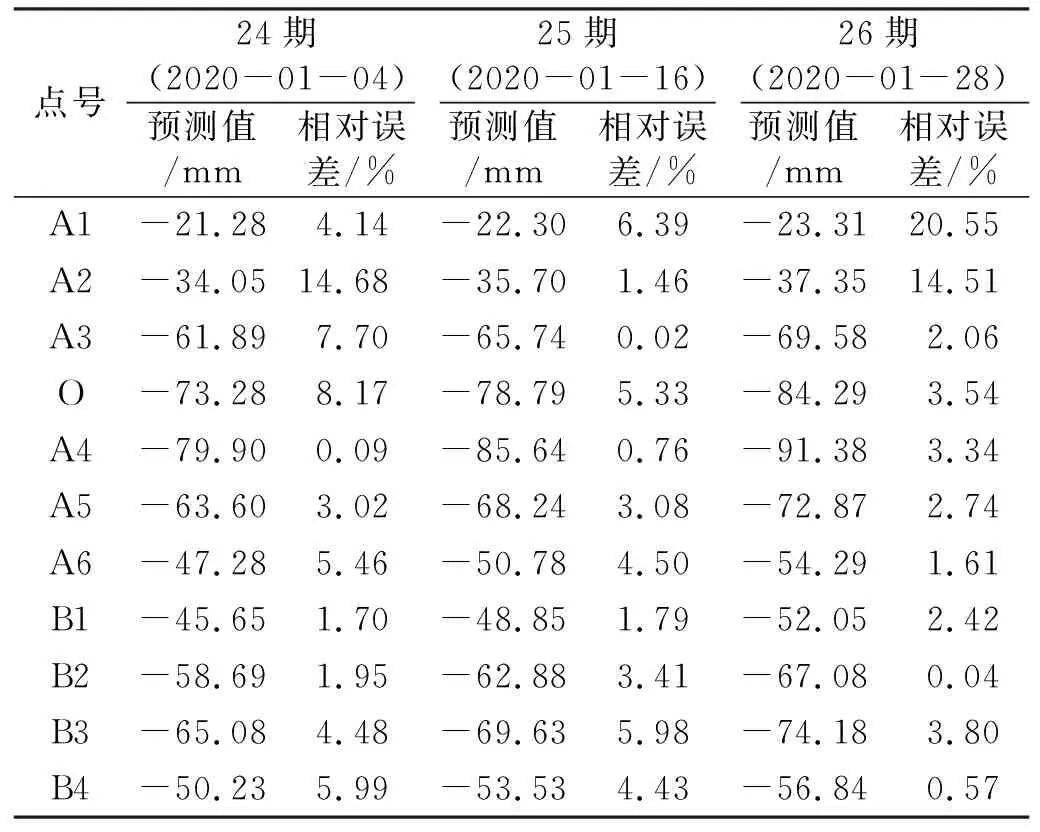
表4 Holt-Winters模型預測值

從表2可以看出，ARIMA模型的均方根誤差RMSE平均值為3.44，略高于Holt-Winters模型，因此Holt-Winters模型的擬合度整體上優于ARIMA模型。但從表3、4可以看出，2種預測模型的預測值與實際值在不同期數不同點的精度存在差異，例如A1點在ARIMA模型下3期預測值的相對誤差分別為19.23 %、0.14 %和18.64 %，在Holt-Winters模型下3期預測值的相對誤差分別為4.14 %、6.39 %和20.55 %，因此引入IOWA算子可克服單一預測方法在不同時間點預測精度不同的缺點。

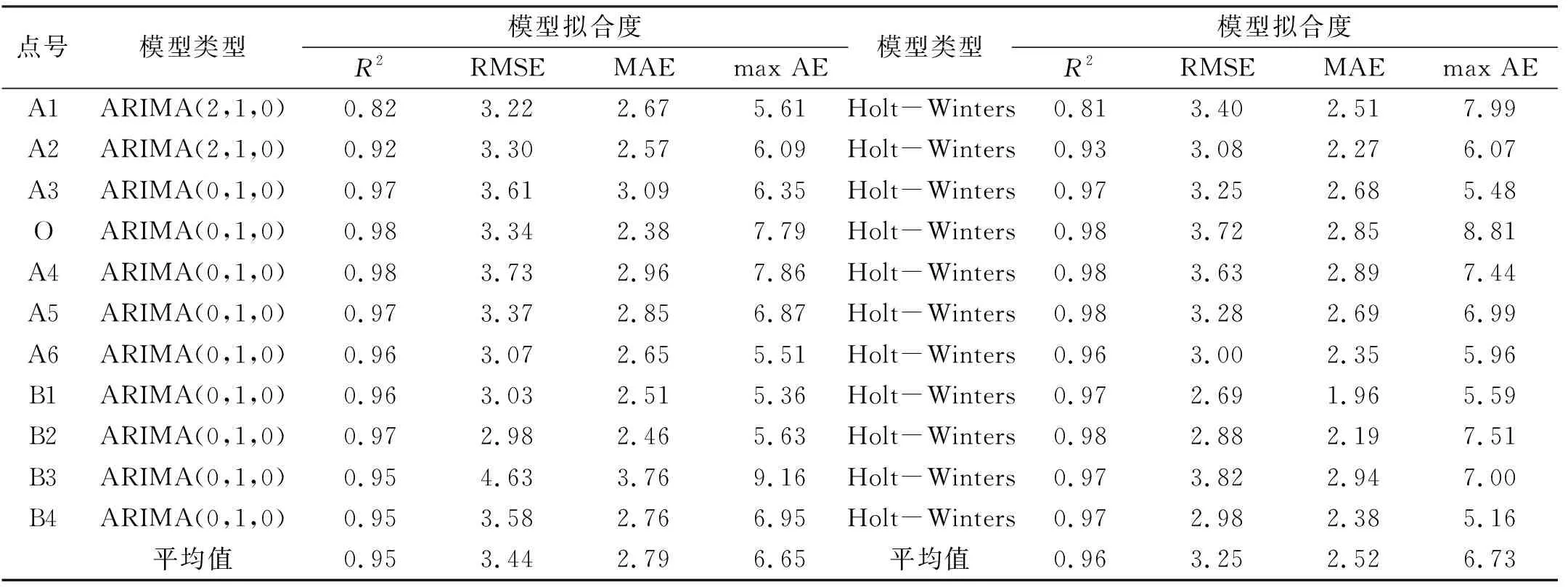
表2 各模型擬合度

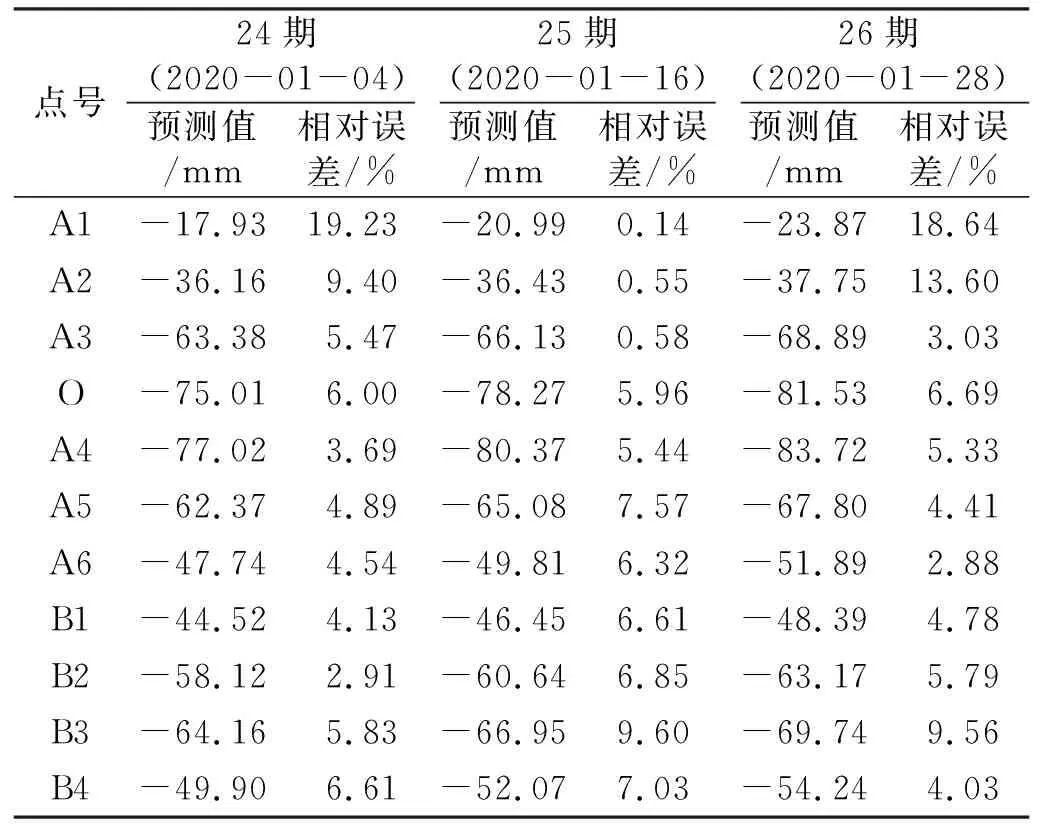
表3 ARIMA模型預測值

方案3基于IOWA算子，由式(11)計算IOWA組合預測值，以A1點為例：

fL[(p1,24,x1,24),(p2,24,x2,24)]=

l1xa-index(1,24)+l2xa-index(2,24)

fL[(p1,25,x1,25),(p2,25,x2,25)]=

l1xa-index(1,25)+l2xa-index(2,25)

fL[(p1,26,x1,26),(p2,26,x2,26)]=

l1xa-index(1,26)+l2xa-index(2,26)

得出：

fL[(0.808,-17.93),(0.959,-21.28)]=

-21.28l1-17.93l2

fL[(0.999,-20.99),(0.936,-22.30)]=

-20.99l1-22.30l2

fL[(0.814,-23.87),(0.794,-23.31)]=

-23.87l1-23.31l2

將其代入式(12)，整理得到最優化模型：

2 811.6l1l2-3 225.42l1-3 098.15l2+1 793.00

同理可得到其他點的最優化模型。利用編程或MATLAB最優化工具箱可計算出A1點基于IOWA算子的組合預測模型的最優權系數為：

l1=1,l2=0

則A1點的預測值分別為-21.28 mm、-20.99 mm和-23.87 mm。

從A1點組合預測模型的IOWA最優權系數可以看出，該方法在A1點的組合預測是將2個單一模型中預測精度更高的值作為其組合預測值。表5為基于IOWA算子的組合預測模型的預測值。

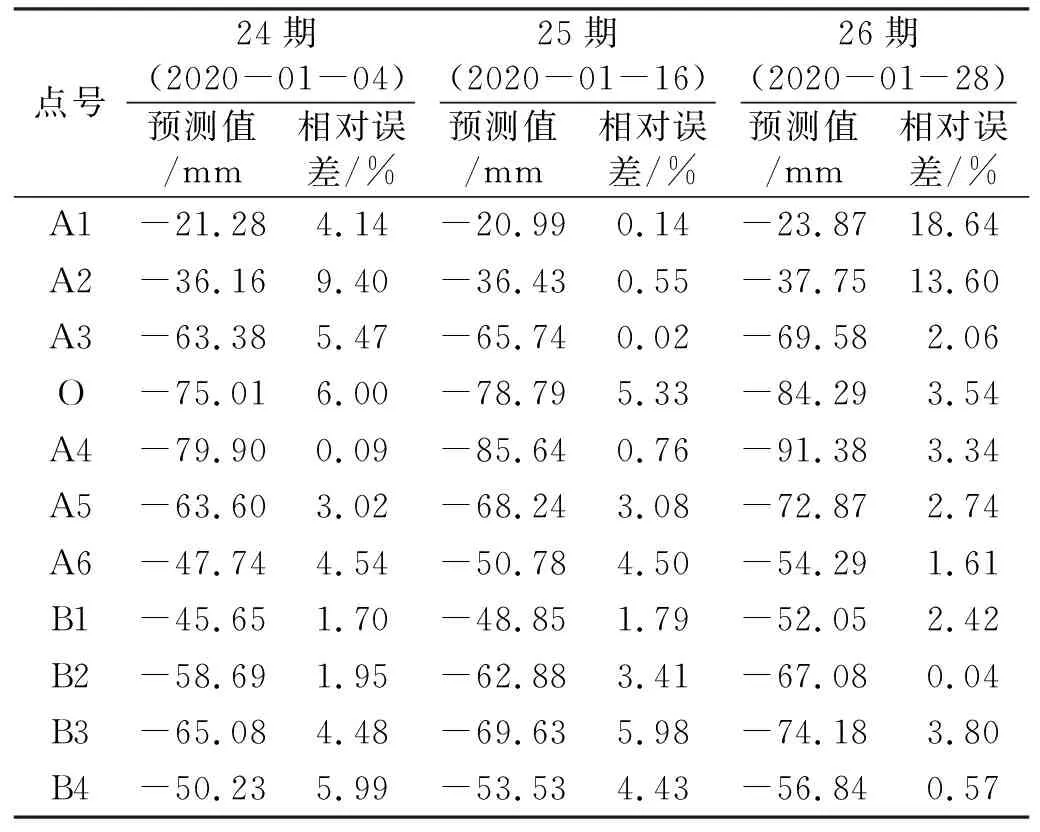
表5 組合預測模型預測值

為驗證上述組合預測模型的有效性，選取均方誤差MSE和平均絕對誤差MAE作為主要評價指標(表6)。

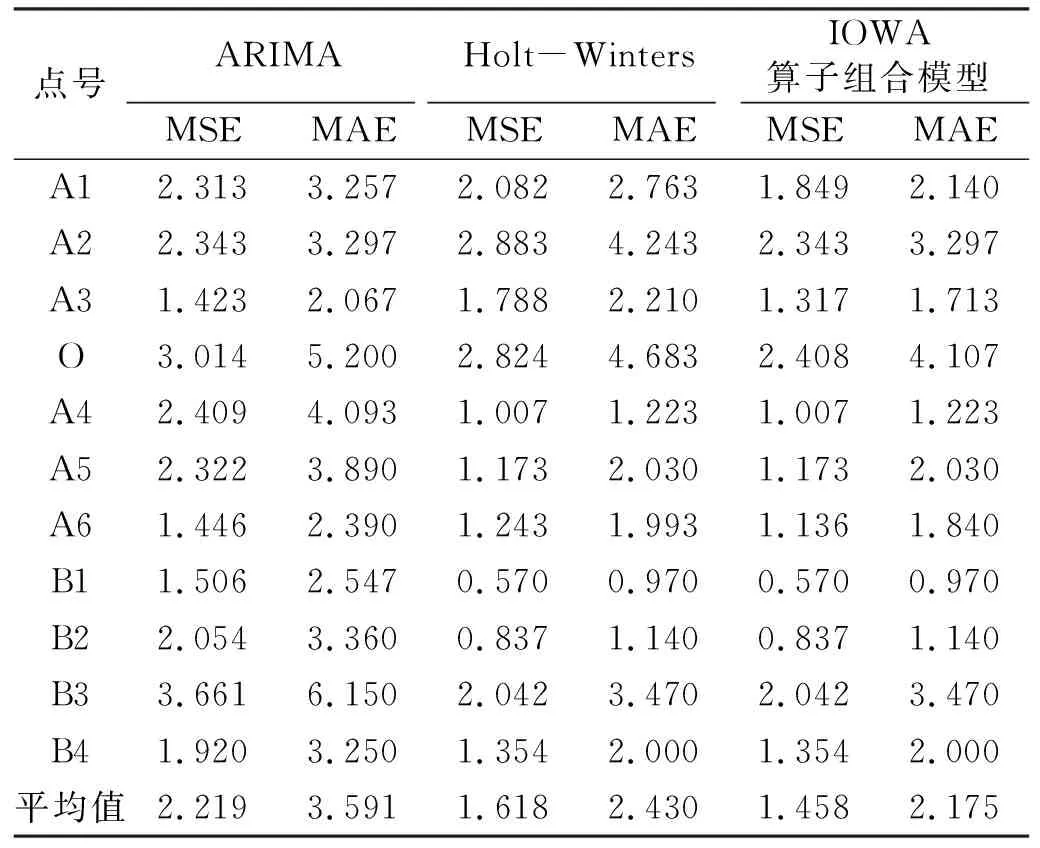
表6 預測精度比較

從表6可以看出，基于IOWA算子的組合模型在各點的均方誤差MSE和平均絕對誤差MAE均比單一模型小，表明該組合模型的預測精度更高，具有一定的有效性。

3 結 語

以金昌市龍首礦西二采為研究區，采用26景SAR影像進行SBAS地表沉降監測，得到該地區26期時序沉降變化與累積沉降值。以SBAS監測值為實際值，基于前23期監測值分別采用ARIMA模型和Holt-Winters模型進行擬合并預測后3期沉降值。結果表明，單一模型在不同點不同時期的預測精度存在差異，其中ARIMA模型在A1、A2、A3點第25期的預測精度更高，Holt-Winters模型則在B1～B4點的預測精度更高。根據各單一模型的預測值特點，本文基于IOWA 算子將ARIMA模型和Holt-Winters模型進行組合，在最優權系數賦值時按照單一模型的預測精度大小進行賦值，組合模型可有效克服傳統單一賦權的缺陷，其精度優于各單一模型。