小波閾值法在JCZ系列超寬頻帶地震儀記錄的地震數據中的應用及探討

王海斌 周云耀 呂永清 向 涯

1 中國地震局地震研究所地震大地測量重點實驗室，武漢市洪山側路40號，430071

JCZ-1超寬頻帶地震儀是“八五”期間研制的頻帶為DC～20 Hz的地震觀測儀器[1]，具有高靈敏度、低噪聲等特點，觀測范圍可從高頻地震波至固體潮[2]。截至2019年，國內已有17個臺站安裝JCZ系列超寬頻帶地震儀，可為地震信號監測提供大量數據。由于地球內部結構復雜，地震儀器采集到的地震信息往往伴隨著各種噪聲，為壓制背景噪聲，保留地震數據波形，需保持較高的信噪比，這對于后續地震數據分析處理具有重要意義。

JCZ系列地震儀可獲取大量來自地球內部的地震信息，除去有效信號外，還包含各種噪聲(主要分為相干噪聲和隨機噪聲[3])。但目前有關該儀器的地震數據去噪處理等方面的研究方法較為單一，本文對地震信號降噪處理中的小波閾值法進行去噪研究，重點探討小波基函數的選取、小波分解幾何尺度參數的確定及軟閾值、硬閾值函數的選取對去噪結果的影響等。同時探討在小震和中強震兩種情況下用相同方法處理的去噪效果，并選擇合適的小波基與幾何尺度用于震例數據去噪對比。結果發現，選取不同的閾值函數在不同震級的地震數據處理中會表現出不同的去噪效果。

1 小波變換與去噪理論

在地震信號處理中，傅里葉變換是一種常用的方法，但該方法在處理非平穩信號時不能在時域和頻域聯合分析[1]。因此，小波變換應運而生，其具有局部化時頻分析功能，時頻窗口的大小可以隨著頻率的高低而變化。當地震信號的低頻部分較為平緩時，所含的頻率成分較多，小波分析可通過降低時間分辨率來提高頻率分辨率；當地震信號的高頻部分包含很多瞬態變化的特征時，小波分析可通過提高時間分辨率來關注信號的瞬態特征，從而降低頻率分辨率[4]。

設地震信號函數為x(t)，其連續小波變換的時域表達式為[1]：

a>0,b∈R

(1)

式中，a為伸縮因子，b為平移因子。a、b均連續變化，ψ*(t)是ψ(t)的共軛，稱為小波變換系數。在實際運用中，需要將參數a、b進行離散化：

(2)

則離散化的小波函數表達式為：

j=0,±1,±2,…;k=0,±1,±2

(3)

降噪的含義是在進行地震信號去噪時盡量將無用的信息從原始信號中去除[4]，應滿足兩條準則：1)降噪處理后的信號大部分情況下應與原始信號具有同等的光滑性；2)降噪處理后的信號和原始信號的方差估計應在最壞情況下方差最小[4]。 本文小波閾值去噪算法如圖1所示。

圖1 小波閾值去噪算法Fig.1 The algorithm of wavelet threshold denoising

2 小波閾值去噪實際操作

2.1 去噪意義

對于去噪后結果的評價，傳統的評價標準有信噪比、平滑度、均方根誤差、互相關系數等。由于JCZ超寬頻帶地震儀采集到的信號是地震信號與噪聲信號的混合信號，很難得到地震信號的純信號，無法使用信噪比進行真正意義上的計算評價。文獻[5]將去噪后的信號當作純信號，將原始信號當作帶噪信號，提出相對信噪比概念，計算公式為：

(4)

式中，SNR*為相對信噪比，P1為小波去噪后的波形，P2為原始波形。相對SNR值越大，表示原始波形越接近去噪后的波形，說明去噪后的波形噪聲依然很高，去噪效果不理想；相對SNR值越小，表示原始波形越遠離去噪后的波形，說明去噪后的波形噪聲較小，去噪效果明顯。對于互相關系數[6]的計算，因為理論參考信號未知，即理論地震信號未知，計算準確度不高，因此本文未采取該衡量標準。平滑度指標的數學解釋為當信號足夠長時，去噪后信號的一階差分與原始信號的一階差分的方差根之比[7]，其值越小，去噪效果越好，計算公式為：

(5)

均方根誤差是指原始信號與去噪信號之間方差的平方根[8]，將采集到的噪聲與地震信息的混合信號作為原始信號，將小波去噪后的信號作為去噪信號。該指標可體現信號的整體偏差信息，數值越小說明去噪效果越好，計算公式為：

(6)

平均絕對誤差可體現去噪后信號與原始信號之間的相似性，數值越小表示去噪效果越好，計算公式為：

(7)

式(5)～(7)中，f(i)為地震計采集到的原始信號，f′(i)為小波去噪后的信號。

每種評價指標均從單一方面評價小波去噪的效果，當真值未知時，任何一種評價指標都無法滿足質量評價的需求[8]。經過一系列實驗發現，在選取小波基的實驗過程中，并不是每種評價標準都能較好地反映不同小波基的去噪效果。在選取小波基的實驗中，RMSE值與相對SNR值作為評判標準的效果比平均絕對誤差和平滑度差，其值變化不明顯，所以選擇平滑度與平均絕對誤差作為小波去噪效果的評價指標。對于分解與重建尺度的選取，去噪后信號的均方根誤差的變化量較小，可以作為最佳分解尺度[9]。

2.2 小波基選取

小波變換具有許多小波基可供選擇，不同的小波基對地震信號去噪結果的影響也不同。對于小波基的選擇，首先理論上要求其具有一定的緊支性、平滑性、對稱性和消失矩階數等，能較好處理地震信號的小波基函數主要有biorthogonal小波、daubechies小波、coifmant小波、symletsA小波[5]。在此基礎上，使用實驗方法對上述4種小波基進行地震信號的降噪處理。本文實驗使用控制變量法，對于小波基的選取，只設置小波基變量，分解層數均設置為1，閾值均采用Birge-Massart閾值，信號上作用閾值的方法均使用硬閾值處理，其中Birge-Massart策略的經驗系數設置為2。

本文實驗數據均來自武漢水院地震臺運行的JCZ-1超寬頻帶地震儀記錄的數據，其中小波基與尺度實驗數據為2016-03-22 00：00開始采集的連續24 h的垂直方向數據，數據格式為miniSEED，從第380 000點開始截取，直至第720 000點，信號長度為340 000。利用4種常用方法進行實驗分析，首先在各自的小波簇內進行比較以確定較好的小波基，然后在選出的4種較好的小波基中進行比較，最終選出最有效的小波基。

由表1可以看出，在db系列的小波基中，采用db6小波基的平滑度最小，平均絕對誤差也最小，說明采用db6小波基是該小波基系列的最佳選擇。

表1 db小波基實驗數據

由表2可以看出，采用coif1小波基的平滑度在coif小波基中最小，表明去噪后的信號局部無過多的突變信息，說明去噪后信號的光滑性最好；但其平均絕對誤差卻很大，表明去噪后的信號與原始信號的相似程度較小；同時小波基coif1的消失矩階數過小，反映小波去噪后的信號重構能量不集中，因此未選擇小波基coif1。由表2可知，從小波基coif1到小波基coif5，隨著平滑度的不斷增大，平均絕對誤差不斷減小，證明小波基無法很好地兼顧平滑性和緊支集性的特點。綜上所述，選取coif3作為該系列的小波基。

表2 coif小波基實驗數據

由表3可以明顯看出，采用小波基bior1.1～bior1.5去噪后信號的平滑度明顯不夠，并且平均絕對誤差相對較大，這是因為這幾個小波基的支撐長度較小。采用小波基bior2.6～bior3.3去噪后信號的光滑性可得到保證，但其平均絕對誤差也相對較大，因為這些小波基隨著濾波器長度的增加，緊支集區間也在變大，使得去噪后信號的平滑度較好，但同時也導致去噪后信號的局部性下降。采用小波基bior3.5～bior4.4去噪后信號的平滑度較好，平均絕對誤差較小，并且這些小波基的消失矩階數較高，信號重構后能量比較集中。綜上可知，bior系列中可選擇平滑度和緊支集性都較好的bior3.5小波基。

表3 bior小波基實驗數據

由表4可以看出，小波基sym4、sym6和sym8的平滑度與平均絕對誤差都較好，比sym系列中其余小波基的效果更好。但對于小波基sym8，其消失矩階數過高，會導致信號重構后能量過于集中；對于小波基sym4，雖然其平滑度最好，但相比于小波基sym6和sym8，其平均絕對誤差過大，表明采用sym4小波基去噪后的信號無過多的局部突變，但會去除過多的有用信息。綜上可知，sym系列可選擇小波基sym6。

表4 sym小波基實驗數據

在每個小波基系列中選出較優的小波基后，再對這4個小波基進行對比，選出最終的小波基(表5)。

由表5可以看出，采用小波基bior3.5去噪后信號的光滑度和平均絕對誤差最好，因此本文選擇bior3.5作為小波基對JCZ超寬頻帶地震儀的地震數據進行去噪。

表5 選出的4種小波基實驗數據

2.3 分解和重構尺度選取

在小波進行地震信號去噪時，分解和重構的尺度對去噪結果具有很大影響，如果小波分解和重構尺度過小，會導致原始地震信號中還存在一定的噪聲數據，消噪效果不理想；如果小波分解和重構尺度過大，會導致去噪后信息大量丟失，信噪比嚴重下降，同時使計算機處理數據的運算量變大[6]。結合前人的研究成果[10-12]，本文設置8組對照實驗，采用控制變量法選用bior3.5小波基，分解和重建尺度為1～8次，使用Birge-Massart閾值，信號上作用閾值的方法均使用硬閾值處理，其中 Birge-Massart策略的經驗系數設置為2(表6)。

表6 不同尺度下的實驗數據

通過計算發現，平均絕對誤差隨分解尺度的增加而不斷增大，相對SNR值則不斷減小；平滑度在分解尺度1～5不斷增加，隨后不斷減少；RMSE值隨著分解尺度的增大而不斷增大，這表明對于本文地震數據去噪分解尺度的選取無法直接使用以上4種評價指標[8]，而去噪后信號的均方根誤差變化量較小時的分解尺度可作為最佳分解尺度[9]。本文通過計算去噪后信號的均方根誤差變化量(表7)發現，當分解尺度為5時變化量最小，因此本文選擇分解和重構尺度為5，其中均方根誤差變化量計算公式為：

表7 不同尺度下的均方根誤差變化量

ver(m)=|RMSE(m+1)-RMSE(m)|

(8)

式中，ver(m)為尺度m+1與尺度m間的均方根誤差變化量，RMSE(m)為第m分解尺度下的均方根誤差。

2.4 小波閾值選取

常用的小波閾值選取方法主要有2種：一是根據原始信號確定各級閾值，原理是基于原始信號的信噪比建立不同的數學模型求取閾值，如本文在選取小波基和分解及構建尺度設計的實驗中使用的Birge-Massart閾值[4]；二是根據樣本數估計選取閾值，原理是在最壞情況下根據降噪信號與原始信號方差最小原則來確定統一閾值[4]。在實驗分析中，除使用Birge-Massart閾值法外，還使用常用的rigrsure、sqtwolog、heursure和minimaxi閾值法進行實驗對比分析。

2.5 小波閾值函數選取

在已選取小波閾值的基礎上，通常采用2種方法將閾值作用到待處理的地震信號上：一是將待處理的地震信號中絕對值小于閾值的點設為零，也稱為硬閾值；另一種方法是在硬閾值基礎上使數據處理邊界出現不連續的點收縮到零[4]。

2.6 兩種不同震級地震數據的去噪實驗

不同頻帶和振幅的地震數據在相同的去噪方法下會表現出不同的效果。為了探討小震和中強震在相同方法下的小波閾值去噪效果，本文使用控制變量法，除地震數據不同外，其余處理方式完全一致，處理方案使用前文選取的小波基與尺度。小震使用JCZ-1超寬頻帶地震儀于2018-08-04在新疆庫爾勒臺記錄到的新疆庫爾勒2.4級地震的垂直向數據，數據從第1 617 400點開始，到第1 622 600點結束。中強震使用JCZ-1超寬頻帶地震儀于2012-12-30在新疆庫爾勒臺記錄到的日本本州4.9級地震的垂直向數據，數據從第466 600點開始，到第495 400點結束。

由圖2～11可以看出，無論是在小震還是在中強震的實際去噪處理中，rigrsure閾值、sqtwolog閾值、heursure閾值和minimaxi閾值在實際地震中的去噪效果均不明顯。由于實際的地震信號噪聲源較多，頻譜覆蓋較廣，基于樣本數估計選取的閾值在實際信號中具有局限性[3]。在小震的小波閾值去噪中，Birge-Massart閾值去噪過度，會去除很多有用信息；在中強震的小波閾值去噪中，Birge-Massart閾值去噪效果較好，可去除地震數據中較多的“毛刺”背景噪聲，保留有效信息。上述分析表明，在對實際的地震信號進行小波閾值去噪處理時，需要進行實際分析才能選出較好的閾值方法。

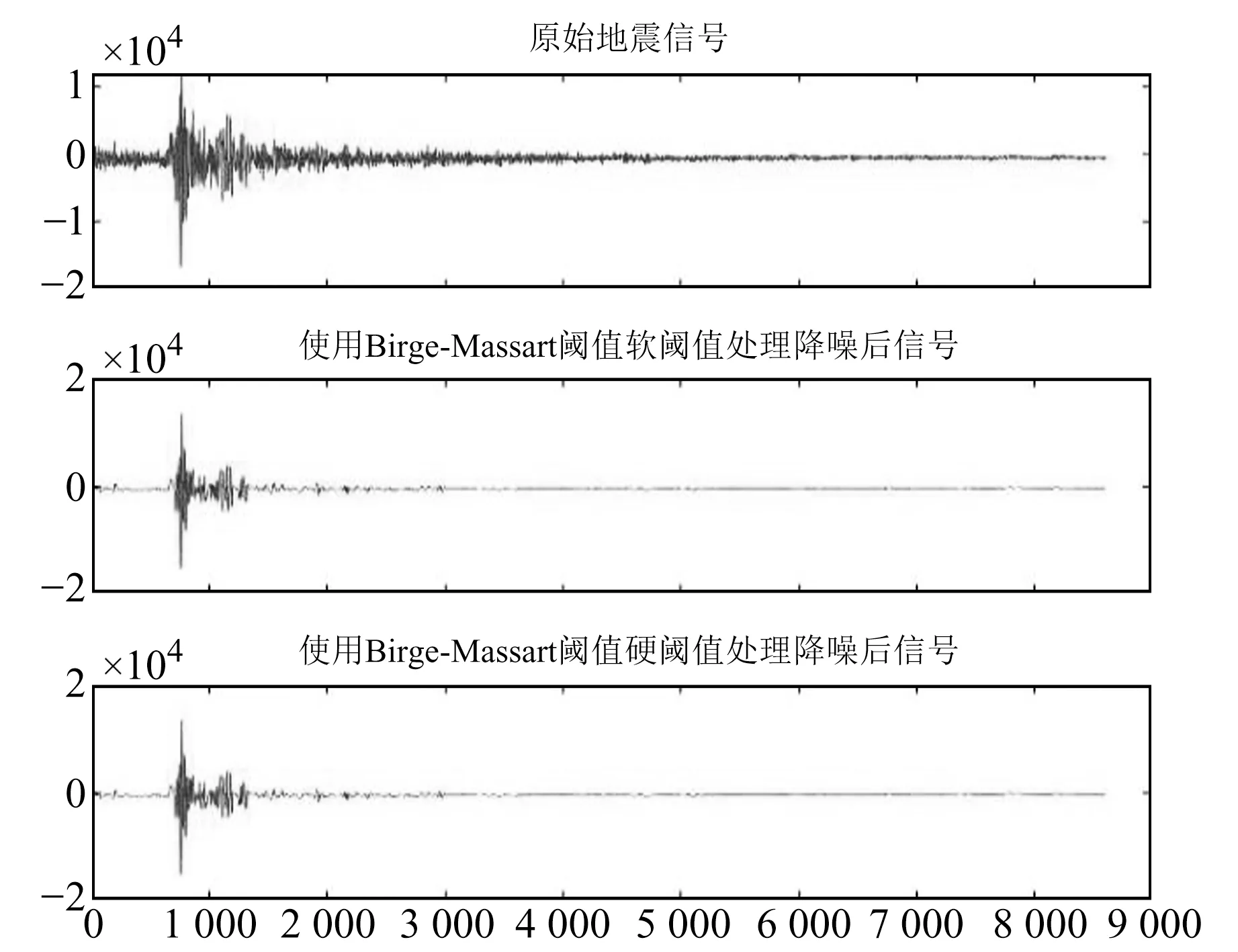
圖2 小震Birge-Massart閾值軟、硬閾值處理后數據與原始數據對比Fig.2 Comparison of the small earthquake data processed by the Birge-Massart soft and hard thresholds and the original data

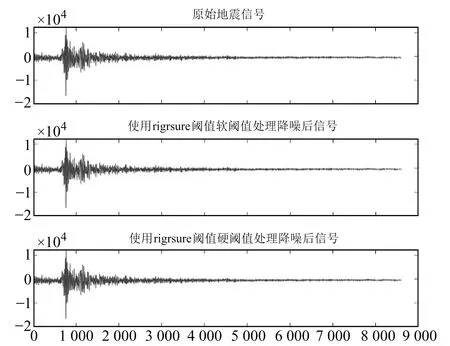
圖3 小震rigrsure閾值軟、硬閾值處理后數據與原始數據對比Fig.3 Comparison of the small earthquake data processed by the rigrsure soft and hard thresholds and the original data

圖4 小震sqtwolog閾值軟、硬閾值處理后數據與原始數據對比Fig.4 Comparison of the small earthquake data processed by the sqtwolog soft and hard thresholds and the original data

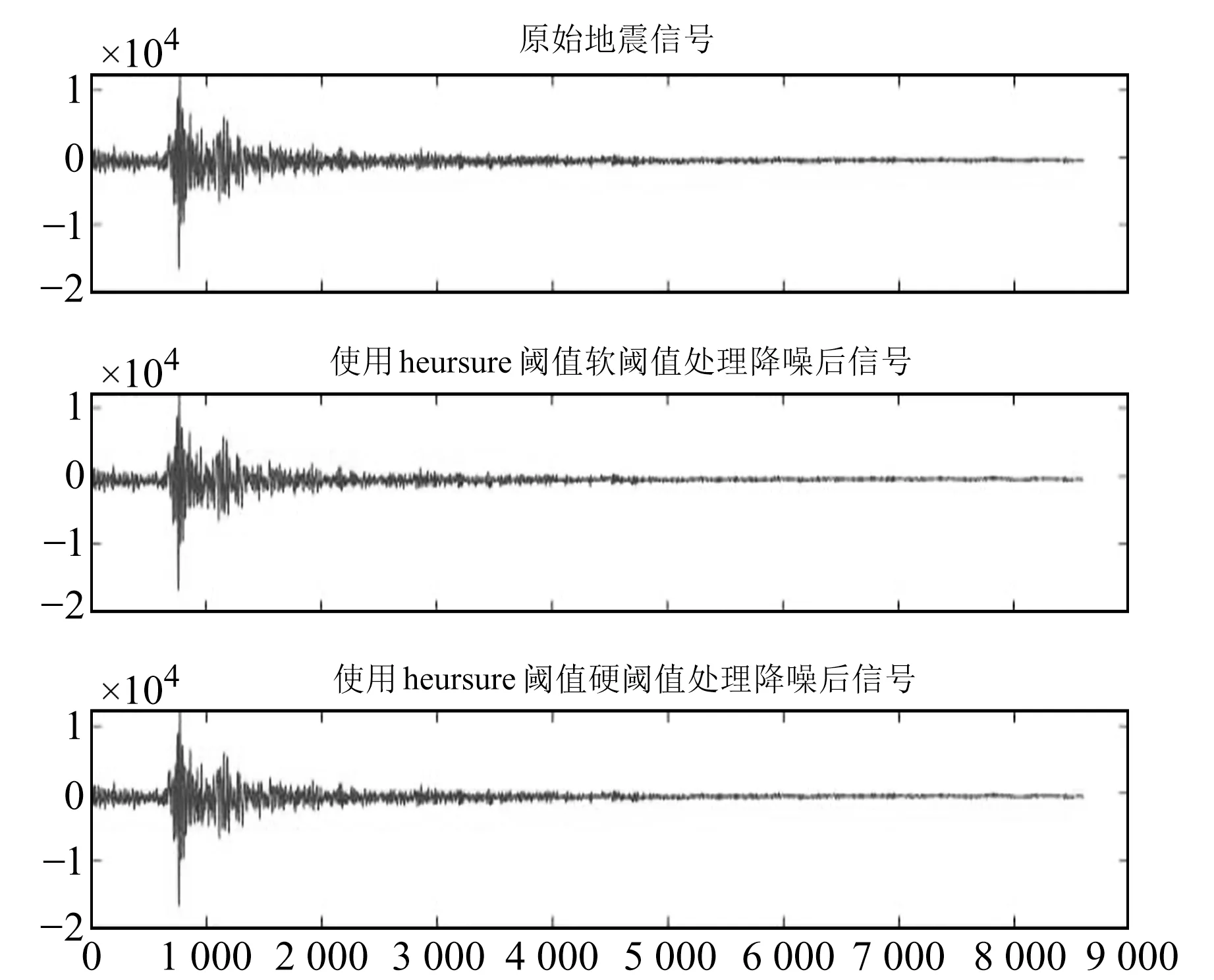
圖5 小震heursure閾值軟、硬閾值處理后數據與原始數據對比Fig.5 Comparison of the small earthquake data processed by the heursure soft and hard thresholds and the original data

圖6 小震minimaxi閾值軟、硬閾值處理后數據與原始數據對比Fig.6 Comparison of the small earthquake data processed by the minimaxi soft and hard thresholds and the original data

圖7 中強震Birge-Massart閾值軟、硬閾值處理后數據與原始數據對比Fig.7 Comparison of the moderate-strong earthquake data processed by the Birge-Massart soft and hard thresholds and the original data

圖8 中強震rigrsure閾值軟、硬閾值處理后數據與原始數據對比Fig.8 Comparison of the moderate-strong earthquake data processed by the rigrsure soft and hard thresholds and the original data

圖9 中強震sqtwolog閾值軟、硬閾值處理后數據與原始數據對比Fig.9 Comparison of the moderate-strong earthquake data processed by the sqtwolog soft and hard thresholds and the original data

圖10 中強震heursure閾值軟、硬閾值處理后數據與原始數據對比Fig.10 Comparison of the moderate-strong earthquake data processed by the heursure soft and hard thresholds and the original data

圖11 中強震minimaxi閾值軟、硬閾值處理后數據與原始數據對比Fig.11 Comparison of the moderate-strong earthquake data processed by the minimaxi soft and hard thresholds and the original data

圖12～13為小震與中強震采用Birge-Massart閾值去噪前后的頻譜圖對比。從圖中可以看出，在采用相同的閾值進行去噪時，針對不同震級的地震會表現出不同的去噪效果。對于小震，Birge-Massart閾值不僅會將高頻段信息去除，也同樣會使低頻段信息失真；對于中強震，Birge-Massart閾值可去除高頻段中部分噪聲，但會保留低頻段的大部分有效信息。

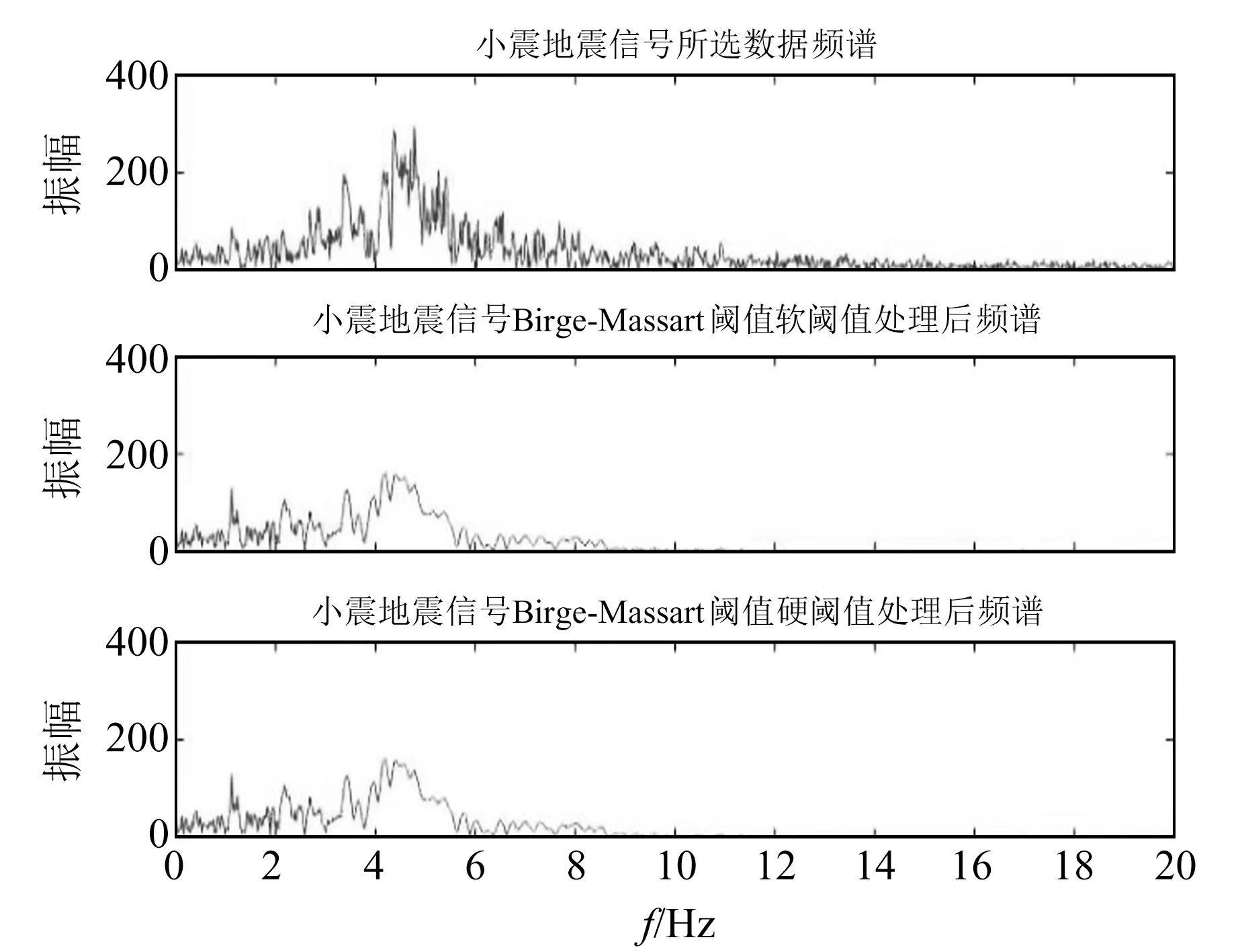
圖12 小震信號所選數據及去噪后頻譜Fig.12 Selected data of small earthquake signal and spectrum after denoising

圖13 中強震所選數據及去噪后頻譜Fig.13 Selected data of moderate-strong earthquake signal and spectrum after denoising

計算中強震去噪后的評價指標，并對比軟閾值與硬閾值處理的效果(表8)。

由表8可以看出，在Birge-Massart小波軟、硬閾值處理后相對SNR值、平均絕對誤差及RMSE值都較為接近，但軟閾值處理后的平滑度明顯優于硬閾值，這也表明軟閾值和硬閾值處理的特點：硬閾值函數在均方根誤差上優于軟閾值，軟閾值函數處理后的重建信號比較光滑。綜合各項指標來看，在Birge-Massart小波閾值去噪中，軟閾值處理的效果比硬閾值好。

表8 中強震Birge-Massart小波閾值處理評價指標

2.7 實際去噪后P波初動的判別探討

JCZ系列超寬頻帶地震儀在全國17個臺站均有布設，地震儀的安置對背景噪聲具有一定要求，因此這些地震儀采集到的地震數據中背景噪聲均較小，從而使P波初動、S波與面波大部分都能被辨別出來。本文選取武漢水院地震臺采集到的2017-01-16蘇門答臘島6.0級地震數據，原始數據中P波初動不明顯，經過去噪后能夠較好地判斷出P波初動(圖14～15)。

圖14 原始數據P波初動判別Fig.14 P wave first motion discrimination from original data

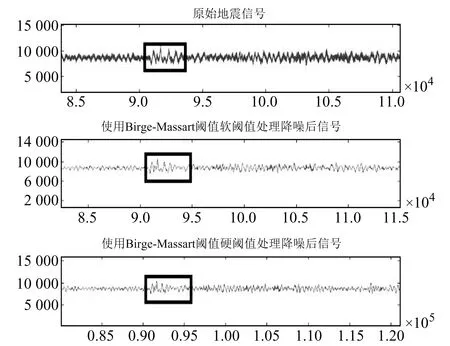
圖15 P波初動判別Fig.15 P wave first motion discrimination

由圖14～15可知，在去噪之前，由于周圍存在噪聲，即使對信號作局部放大觀察，也不能很好地判斷P波初動的位置；但經過Birge-Massart閾值處理后，將P波初動周圍的噪聲進行壓制，可以較好地觀察出P波初動的位置，尤其是經過軟閾值處理后效果更好。

3 結 語

本文使用控制變量法設置實驗，對JCZ系列超寬頻帶地震儀采集到的地震數據采用小波閾值法進行去噪處理。去噪步驟可分為小波基選取、小波分解與重建尺度選取、閾值選取及閾值作用方式選取，并重點討論小波去噪后信號評價指標的選取。對于原始信號中含有噪聲的情況，單一的評價指標不能很好地判斷去噪效果，需要多種指標聯合評價。本文對于閾值處理方式僅分別討論硬閾值與軟閾值處理方法，其實也可將軟、硬閾值結合起來進行數據比較分析，這也是后續研究的重點。通過對比相同方案下的去噪結果可知，在實際地震數據去噪中，基于樣本估計選取的閾值具有一定局限性；在不同震級的地震中，相同閾值的去噪效果可能并不相同。在對P波初動不明顯的地震數據進行去噪后發現，小波閾值去噪對于P波初動的判別具有一定意義。