運載火箭多體動力學(xué)建模與仿真技術(shù)研究

李 東，楊云飛，胡鵬翔，張 歡,4，程 興

(1.北京航空航天大學(xué)宇航學(xué)院，北京 100191；2.中國運載火箭技術(shù)研究院，北京 100076；3.北京宇航系統(tǒng)工程研究所，北京 100076；4.清華大學(xué)航天航空學(xué)院，北京 100084)

0 引 言

2016年6月和11月，我國新一代中、大型運載火箭相繼首飛成功。為提高控制能力，新一代火箭采用助推發(fā)動機搖擺姿態(tài)控制技術(shù)，從飛行結(jié)果看，火箭剛體、晃動、彈性運動穩(wěn)定，新型控制方法的正確性得到驗證[1]。

新一代火箭模態(tài)特性復(fù)雜，存在大量助推局部變形為主的模態(tài)(如圖1所示)。相比傳統(tǒng)火箭，新一代火箭有以下特點值得重點關(guān)注[2]：

圖1 助推局部模態(tài)圖

1)整體火箭呈現(xiàn)出低頻密頻模態(tài)、強耦合振動、復(fù)雜的局部變形等特征，低階模態(tài)中含有大量“呼吸”、扭轉(zhuǎn)、反向彎曲等局部模態(tài)，模態(tài)特征比單根火箭的模態(tài)復(fù)雜很多[2-4]；

2)使用大推力發(fā)動機導(dǎo)致傳動裝置-擺動發(fā)動機系統(tǒng)的固有頻率很低，可能和箭體彈性振動發(fā)生耦合；

3)通過助推發(fā)動機搖擺，將發(fā)動機局部模態(tài)引入控制回路。

引入一種合適的分析手段，實現(xiàn)對動力學(xué)與控制耦合關(guān)系的準(zhǔn)確分析，是新一代運載火箭在設(shè)計過程中無法繞過去的環(huán)節(jié)。為此提出了基于多體動力學(xué)虛擬樣機開展動力學(xué)建模與仿真分析的驗證新方法。

1 多體動力學(xué)技術(shù)發(fā)展現(xiàn)狀

航天器(大型空間站，航天飛機，運載火箭，月球車等)，機器人，高速車輛以及精密儀器等現(xiàn)代工程技術(shù)的發(fā)展，對大型復(fù)雜機械系統(tǒng)的動力學(xué)設(shè)計與分析提出了越來越迫切的需求。伴隨現(xiàn)代計算技術(shù)的迅猛發(fā)展，多體動力學(xué)方法及軟件應(yīng)運而生。總的來說，多體動力學(xué)方法將復(fù)雜機械系統(tǒng)建模成彼此相互連接的多個剛體或柔性體構(gòu)成的系統(tǒng)，對其施加各種載荷、約束、接觸和碰撞等，進行模擬實際過程的動力學(xué)仿真[5]。多體動力學(xué)方法以不斷發(fā)展的數(shù)字計算技術(shù)為保障，基本不受系統(tǒng)自由度規(guī)模和模型復(fù)雜度的限制。

多體動力學(xué)的發(fā)展歷程主要可歸納為三大階段[6-8]。第一個階段是20世紀60年代至80年代中期的多剛體系統(tǒng)動力學(xué)階段。機械工程領(lǐng)域的需求促進多剛體動力學(xué)萌芽并逐步發(fā)展成熟。這一時期的代表性研究包括Wittenburg，Haug和Schiehlen等人的工作。同時，涌現(xiàn)出了一批應(yīng)用廣泛的多體動力學(xué)分析軟件，如ADAMS，DADS和SIMPACK等。

第二個階段是20世紀80年代至今的多柔體系統(tǒng)動力學(xué)階段。由于生產(chǎn)的發(fā)展和生活的進步給工程機械和工業(yè)產(chǎn)品的性能提出了越來越高的要求，廣泛應(yīng)用于工業(yè)領(lǐng)域的多體動力學(xué)方法逐漸發(fā)展為多柔體系統(tǒng)動力學(xué)。小變形柔性多體動力學(xué)最先發(fā)展起來并受到研究者們的極大關(guān)注，代表性的研究有Shabana和Huston等人的工作。研究者們提出了多種小變形柔性體的建模方法，其中應(yīng)用最廣泛的是浮動坐標(biāo)系方法和有限段方法。大變形柔性多體動力學(xué)的發(fā)展始于上世紀末。Shabana等最先提出了大變形柔性體建模的全新方法——絕對節(jié)點坐標(biāo)方法。十多年來，絕對結(jié)點坐標(biāo)方法一直是多體動力學(xué)研究領(lǐng)域的熱點方向之一。Yakoub等、Shabana等和Von等用絕對節(jié)點坐標(biāo)方法研究了大變形梁的動力學(xué)建模，Dmitrochenko等給出了基于絕對結(jié)點坐標(biāo)方法的二維有限元板單元，Gerstmayr等則將絕對結(jié)點坐標(biāo)法引入到三維實體有限元之中。這一階段出現(xiàn)的較成熟的多體動力學(xué)分析商業(yè)軟件有RecurDyn等。

第三個階段是本世紀初至今的多場多學(xué)科多體動力學(xué)階段。工程實際需求導(dǎo)致多場多學(xué)科耦合的多體動力學(xué)分析逐漸進入人們的視野。Moller等將多體動力學(xué)應(yīng)用于“流體-結(jié)構(gòu)”耦合的動力學(xué)仿真研究。Samin等給出了機電系統(tǒng)的多體動力學(xué)建模方法。Liu等分析研究了熱載荷作用下的多體系統(tǒng)動力學(xué)行為。多場多學(xué)科多體動力學(xué)的發(fā)展方興未艾，必將使基于數(shù)值仿真的動力學(xué)設(shè)計和分析能力達到空前的高度，促進人類各領(lǐng)域的工程技術(shù)不斷向前發(fā)展。

國內(nèi)的多體動力學(xué)研究始于20世紀80年代[6-8]。劉延柱、袁士杰、黃文虎、陸佑方、洪嘉振、齊朝輝等分別撰寫了關(guān)于多體動力學(xué)的研究專著，針對多體系統(tǒng)的建模方法和數(shù)值算法展開了較全面的論述。國內(nèi)開發(fā)的通用多體動力學(xué)分析軟件并不多見，其中包括上海交通大學(xué)洪嘉振等人開發(fā)的CADAMB軟件以及清華大學(xué)任革學(xué)等人開發(fā)INSIDES[8]軟件。其中INSIDES具有針對大規(guī)模大變形柔性系統(tǒng)開展仿真分析的能力，該軟件在各個系統(tǒng)領(lǐng)域均有較多的應(yīng)用案例[9-11]，其正確性和穩(wěn)定性已經(jīng)得到了工程實際的驗證。

2 多體虛擬樣機運用到火箭上的優(yōu)勢

2.1 基本思路

典型的運載火箭姿態(tài)控制回路原理[12]如圖2所示。

圖2 姿態(tài)控制回路動力學(xué)模型示意

在傳統(tǒng)火箭設(shè)計，多基于牛頓-歐拉矢量力學(xué)推導(dǎo)，獲取代數(shù)-微分方程形式描述的火箭動力學(xué)方程[12]。其中，運載火箭質(zhì)心平動的動力學(xué)方程組為：

(1)

式中：Fx,Fy,Fz為重型運載火箭在速度坐標(biāo)系中受到的所有外力，包括重力、發(fā)動機推力、發(fā)動機擺動慣性力、氣動力、氣動阻尼力、液體推進劑晃動力以及其他內(nèi)外干擾力等；m為火箭質(zhì)量，V為火箭的速度，θ為旋轉(zhuǎn)彈道傾角，σ為彈道偏角。

箭體繞質(zhì)心轉(zhuǎn)動的動力學(xué)方程組：

(2)

式中：Jx,Jy,Jz為箭體繞箭體系三軸的轉(zhuǎn)動慣量。Mx,My,Mz為作用在箭體7上的各種外力對箭體質(zhì)心的力矩，ωx,ωy,ωz為運載火箭旋轉(zhuǎn)角速率。

采用廣義位移算子表達的彈性振動方程為[2]：

(3)

式中：n為考慮的模態(tài)階數(shù)。ωi，ξi，qi，Qi和Mi為對應(yīng)第i階模態(tài)的頻率、阻尼比、廣義位移算子、廣義力和廣義質(zhì)量。

更多關(guān)于運載火箭的經(jīng)典的姿態(tài)動力學(xué)方程請讀者參考相關(guān)文獻[13-14]。對于新一代火箭，由于彈性模態(tài)異常復(fù)雜、剛體-晃動-彈性運動交聯(lián)嚴重，采用代數(shù)-微分方程形式描述的姿態(tài)動力學(xué)模型會更加復(fù)雜[2]，而且模型具有在地面難以驗證其正確性的困難。如果采用多體虛擬樣機仿真技術(shù)，則可以用多體虛擬樣機替代上述代數(shù)-微分方程(如圖2所示)。

基本思路是：采用結(jié)構(gòu)動力學(xué)軟件(Nastran等)建立火箭結(jié)構(gòu)動力學(xué)模型，經(jīng)過適當(dāng)轉(zhuǎn)化，生成多體仿真軟件可以識別的模型，該模型將自動包含火箭完整的剛體-彈性-晃動運動信息，增加外力函數(shù)與控制器后，可以直接驅(qū)動虛擬樣機仿真。將同等外力條件下，虛擬樣機與代數(shù)-微分方程仿真結(jié)果進行對比，可以實現(xiàn)對模型驗證等。采用經(jīng)過驗證的虛擬樣機模型，可以進一步開展動力學(xué)耦合分析。

2.2 建模原理分析

運載火箭可看成一個彈性體，在彈性體上定義一個浮動坐標(biāo)系(如圖3所示)，當(dāng)浮動坐標(biāo)系確定后，彈性體上任意點的運動都可以唯一地分解為浮動坐標(biāo)系的剛體運動和基于浮動坐標(biāo)系的彈性運動[5]

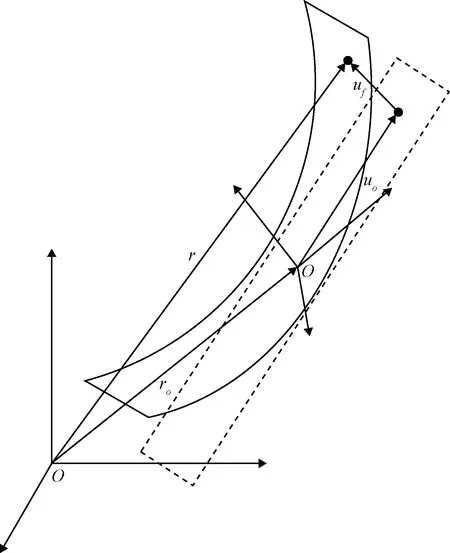
圖3 彈性體上浮動坐標(biāo)系定義

r=ro+A(u0+uf)

(4)

式中：r為質(zhì)點位置矢量，ro為彈性體質(zhì)心位置矢量，u0為變形前彈性體上質(zhì)點在浮動坐標(biāo)系位置，A為浮動系和參考系的轉(zhuǎn)移矩陣。

uf為該點因彈性變形導(dǎo)致的位移在浮動坐標(biāo)系內(nèi)的坐標(biāo)向量，即該點彈性變形的大小。

uf=NTqf=∑Niqfi

(5)

式中：Ni為彈性體第i階模態(tài)振型在該點的取值，qf為彈性體浮動坐標(biāo)系原點位移彈性坐標(biāo)(采用模態(tài)坐標(biāo))。

彈性體上任意點的速度向量可以由位移對時間求導(dǎo)得到：

(6)

(7)

由于彈性振動還會引起附加的角速度，因此任意點的局部角速度向量為：

(8)

式中：N′i為彈性體第i階模態(tài)振型空間導(dǎo)數(shù)在該點的取值。

從分析力學(xué)出發(fā)建立多體動力學(xué)模型，各單元的基本形式為[5]

(9)

式中：T為系統(tǒng)動能，q為廣義坐標(biāo)，Qe為表示廣義力；Cq為約束方程；λ為拉氏乘子。

將結(jié)構(gòu)體各個單元的分析力學(xué)模型組裝，采用大規(guī)模的數(shù)值求解技術(shù)獲得數(shù)值解，這就是多體仿真的核心思想。

從上述模型基礎(chǔ)出發(fā)，也可以推導(dǎo)解析形式的全箭整體的姿態(tài)動力學(xué)模型。

廣義坐標(biāo)系定義為：q=[ro,θ,qf]T，其中，ro=[xo,yo,zo]T為彈性體浮動坐標(biāo)系原點位移，θ=[γ,ψ,φ]T為彈性體浮動坐標(biāo)姿態(tài)坐標(biāo)(采用歐拉角表示)。

由任意點速度向量的定義式，可以得到動能的表達式為：

(10)

式中：A，ω′和qf由廣義坐標(biāo)決定，與點的位置無關(guān)，可以提取到積分號外，其他積分內(nèi)的項與廣義坐標(biāo)無關(guān)，即與時間無關(guān)，是由彈性體本身材料和剛度決定的，與彈性體的運動和受力情況無關(guān)，由這些積分項可以定義9個不變量，如表1所示。

表1 不變量列表

根據(jù)這些不變量，可以簡化動能表達式。同時利用ω′和廣義坐標(biāo)的關(guān)系式，考慮飛行中的火箭為雙端自由的狀態(tài)(即無約束)，可以推出火箭的基本動力學(xué)方程組，包括平動方程(與ro相關(guān))，轉(zhuǎn)動方程(與ω′相關(guān))和彈性振動方程(與qf相關(guān))。

針對運載火箭，深入的數(shù)值分析表明，I0、I6、I5分別在平動方程、轉(zhuǎn)動方程和彈性振動方程中占主導(dǎo)地位，其他不變量在各方程中相對數(shù)值很小，可以忽略。其中：平動方程中省略耦合項的影響大小由I2與I0的數(shù)值相對大小決定，轉(zhuǎn)動方程中省略耦合項的影響大小由I2，I3，I4，I7，I8與I6的數(shù)值相對大小決定，振動方程中省略耦合項的影響大小由I2，I3，I4，I7，I8與I5的數(shù)值相對大小決定。數(shù)值計算表明：在大型火箭模型中，這些項的數(shù)值比一般在千分之一數(shù)量級。因此當(dāng)彈性振動位移和相應(yīng)的振動速度不是非常大時，可以將這些耦合項略去，從而動力學(xué)方程可以退化為解耦的平動方程、轉(zhuǎn)動方程以及振動方程。退化后的方程一般形式如下：

平動方程，即牛頓方程：

(11)

轉(zhuǎn)動方程：

(12)

振動方程：

(13)

注1:由于式(9)中沒有引入勢能項，因此彈性回復(fù)力和阻尼力在方程中都通過廣義彈性力實現(xiàn)，即上述方程左端2、3項。

將平動方程在速度坐標(biāo)系中投影，將轉(zhuǎn)動方程與振動方程進一步分解，同時對剛體運動同樣引入線性化假設(shè)等[2]，就可以得到與2.1節(jié)一致的動力學(xué)方程。

上述的推導(dǎo)過程顯示，對火箭而言，多體模型本質(zhì)上和傳統(tǒng)的姿態(tài)動力學(xué)模型是一致的。但由于多體仿真實際上是基于各單元模型(式9)直接展開，因此可以充分體現(xiàn)在解析模型推導(dǎo)過程中被忽略的各項耦合因素的影響。

2.3 引入多體仿真技術(shù)的意義

傳統(tǒng)火箭設(shè)計中所普遍采用的“代數(shù)-微分方程組”是對物理本質(zhì)的高度抽象化，具有形式簡潔的特點，理論上具備獲取解析解的可能。但是對于捆綁火箭這樣復(fù)雜的系統(tǒng)，由于方程階數(shù)高、參數(shù)多、耦合關(guān)系復(fù)雜，使得解析解的求解難度大，為了求解必須做大量假設(shè)，將模型進行小偏差線性化處理，可能導(dǎo)致設(shè)計或仿真結(jié)果偏離真實狀況。比如，在火箭飛行力學(xué)數(shù)學(xué)模型的推導(dǎo)過程中，對于結(jié)構(gòu)變形要基于小變形假設(shè)，建模過程中會忽略各種非線性、強耦合的因素。

如果在數(shù)值仿真中采用多體動力學(xué)模型替代飛行力學(xué)模型，則容易避免飛行力學(xué)推導(dǎo)過程出現(xiàn)的錯誤，獲得更加可信的仿真結(jié)果。對于模態(tài)呈現(xiàn)空間分布特點、助推器和發(fā)動機-伺服系統(tǒng)存在局部低頻模態(tài)，剛-晃-彈運動耦合嚴重的新一代大型捆綁火箭而言，這一優(yōu)點顯得尤其可貴。與純“代數(shù)-微分方程組”建模與分析方法相比，基于多體動力學(xué)虛擬樣機模型分析，具有如下優(yōu)勢及特點：

1)多體動力學(xué)模型可以使用空間三維結(jié)構(gòu)動力學(xué)模型，相比用于傳統(tǒng)模態(tài)計算用火箭梁模型，表達信息更為全面、準(zhǔn)確，更適合于針對復(fù)雜結(jié)構(gòu)開展動力學(xué)耦合分析；

2)多體動力學(xué)模型可實現(xiàn)“復(fù)雜結(jié)構(gòu)(含流體)動力學(xué)-控制”的一體化仿真，直接仿真推進劑消耗過程，是更為接近物理本質(zhì)的模型，避免推導(dǎo)數(shù)學(xué)模型帶來的大量簡化，完整地保留了火箭各系統(tǒng)之間的耦合關(guān)系；

3)多體動力學(xué)模型直接基于結(jié)構(gòu)模型進行仿真，能夠充分表達全箭復(fù)雜的彈性模態(tài)特性，沒有人為的模態(tài)舍棄現(xiàn)象，更沒有基于“代數(shù)-微分方程”仿真所面臨的大量模態(tài)排列、模態(tài)插值等問題[12]，降低了設(shè)計風(fēng)險；

4)基于多體動力學(xué)模型可以方便、直觀的提取全箭所有位置姿態(tài)與振動響應(yīng)。通過一次仿真，可以提煉有控制作用下的載荷、晃動幅值，分離體的動態(tài)間隙等信息。可以開展關(guān)鍵參數(shù)敏感分析，也可以對推力偏差、推力不同步、氣動偏差等干擾因素開展更加符合物理本質(zhì)的仿真，這一點相比數(shù)學(xué)模型具有很大的優(yōu)勢。

3 新一代火箭多體建模與仿真

要構(gòu)建一個運載火箭多體虛擬樣機模型，需要完成建模包括：結(jié)構(gòu)虛擬樣機模型、變質(zhì)量液體模型、發(fā)動機推力模型、分布式氣動力模型、導(dǎo)航制導(dǎo)與控制模型、環(huán)境參數(shù)計算模型等。由于全部的內(nèi)容非常龐大，本文僅以采用INSIDES軟件建模為例做必要的闡述。

1)箭體結(jié)構(gòu)虛擬樣機

采用有限元軟件Nastran建立火箭結(jié)構(gòu)動力學(xué)模型(如圖4所示)，然后翻譯為多體軟件INSIDES識別的語言，轉(zhuǎn)化過程可采用Matlab程序?qū)崿F(xiàn)。轉(zhuǎn)化完成后形成結(jié)構(gòu)INS文件。有關(guān)INSIDES語法，讀者可以參考文獻[15]。

圖4 箭體結(jié)構(gòu)模型

多體軟件可以對結(jié)構(gòu)有限元模型進行特征值分析，通過特征值校核，可以判斷轉(zhuǎn)化過程的正確性[2]。

2)變質(zhì)量充液貯箱模擬

運載火箭中有90%為液體，液體隨推進劑時間快速消耗，如何準(zhǔn)確模擬推進劑消耗過程、箭體質(zhì)量特性的變化，以及質(zhì)量流動帶來的慣性力、哥式力，是多體運用到火箭設(shè)計中的一個難點。為此，胡鵬翔等[16]提出了一種全新的多體單元建模方法。

基于文獻[16]提供的方法，在多體中建立各個貯箱的變質(zhì)量單元(如圖5所示)。仿真前還需要配置必要的參數(shù)，這些參數(shù)包括各個貯箱中推進劑隨時間變化的液面高度、液體質(zhì)量、質(zhì)量變化速度、質(zhì)量變化加速度、晃動質(zhì)量與晃動頻率等信息。這些參數(shù)，可以離線計算出來，然后采用文本文件的方式裝訂。如果強調(diào)對飛行故障或偏差進行實時模擬仿真，則可以將計算液體質(zhì)量特性的過程編寫成一個C++函數(shù)，通過DLL方式編譯到多體程序中[15]。

圖5 變質(zhì)量充液貯箱的多體模型

3)推力模型

在多體軟件中，通過外力函數(shù)方式加入推力。雖然大部分時候，運載火箭推力恒定，但實際上火箭為變推力系統(tǒng)，在點火、大氣層飛行、關(guān)機、各級轉(zhuǎn)段、過程中，火箭推力會發(fā)生變化。為實現(xiàn)推力準(zhǔn)確模擬，可以編寫推力模擬函數(shù)，采用DLL形式編譯到多體軟件中。

4)氣動力模型

在傳統(tǒng)的姿態(tài)動力學(xué)數(shù)學(xué)模型中，往往采用等效的集中氣動力、集中力矩形式模擬氣動力作用[12]。

在多體軟件中，為模擬火箭真實受力的物理過程，需要采用分布式的氣動力系數(shù)，模擬作用火箭結(jié)構(gòu)模型上氣動力。氣動力施加方式的差異是多體仿真區(qū)別于一般仿真的一個重大差異。

火箭各部段結(jié)構(gòu)承受分布式氣動載荷節(jié)點示意如圖6所示。

圖6 箭體結(jié)構(gòu)承受氣動載荷節(jié)點示意

考慮氣流與風(fēng)的影響，實時計算各個節(jié)點局部攻角αi、βi[12]，則各個節(jié)點上三個方向的氣動力可寫為：

Fx(i)=0.5×CdqSM

(14)

Fy(i)=0.5×CNα(αi)qSM

(15)

Fz(i)=0.5×CNβ(βi)qSM

(16)

式中：Cd為軸向力系數(shù)、CNα(αi)、CNβ(βi)分別為法向與橫向氣動力系數(shù)，q為速度頭，SM為氣動參考面積。由于氣動力系數(shù)是按照由作用節(jié)點所構(gòu)成的梁段賦值，而多體模型中作用在各個節(jié)點上的氣動力由前后兩個節(jié)點承擔(dān)，故在各節(jié)點的氣動力表達式前乘以系數(shù)0.5。具體實現(xiàn)上，可以采用C++編寫DLL程序，實現(xiàn)添加分布式氣動力的功能。

5)控制器模型

運載火箭的控制器包括導(dǎo)航、制導(dǎo)與姿態(tài)控制功能模塊，相關(guān)形式請讀者參考文獻[17-19]。

如果只單獨考慮姿態(tài)控制作用，則可以將控制方程寫成狀態(tài)空間模型形式，多體軟件支持狀態(tài)空間模型的實現(xiàn)形式，也編寫單獨的DLL函數(shù)實現(xiàn)控制功能。一些多體軟件，比如Adams支持和Matlab軟件之間的交互仿真[6]。

6)其它

其它待實現(xiàn)的功能，包括從結(jié)構(gòu)虛擬樣機上獲取特征位置在慣性空間下的位置、速度、加速度、角度信息；計算并輸出馬赫數(shù)Ma、飛行高度H、飛行速度V、大氣密度參數(shù)；輸出發(fā)動機擺角信息、關(guān)機信息；重力函數(shù)的實現(xiàn)等，這些都可以采取多體軟件支持的語法與函數(shù)形式實現(xiàn)，在此不再贅述。

采用上述方法，實現(xiàn)的一個火箭多體虛擬樣機模型如圖7所示，其中一組發(fā)動機-伺服系統(tǒng)局部放大圖形如圖8所示。

圖7 火箭多體虛擬樣機

圖8 多體模型(發(fā)動機-伺服局部放大)

4 仿 真

針對新一代火箭，采用多體虛擬樣機模型與控制參數(shù)進行仿真，部分仿真結(jié)果如圖9～11，仿真顯示：

圖9 三通道姿態(tài)角偏差

1)三通道姿態(tài)角與角速度穩(wěn)定，且姿態(tài)變化與傳統(tǒng)姿態(tài)動力學(xué)模型仿真結(jié)果一致;

2)全箭彈性、晃動運動穩(wěn)定，在干擾作用下的振動幅值均收斂；

3)發(fā)動機擺角穩(wěn)定，發(fā)動機-伺服系統(tǒng)未現(xiàn)局部的振蕩。

基于多體研究方法表明：1)新一代火箭“代數(shù)-微分”形式姿態(tài)動力學(xué)模型正確；2)基于新一代火箭“代數(shù)-微分”姿態(tài)動力學(xué)模型設(shè)計得到的姿態(tài)控制參數(shù)可以確保整個飛行過程姿態(tài)的穩(wěn)定。

圖10 三通道姿態(tài)角速度

圖11 發(fā)動機擺角

5 結(jié) 論

由于多體仿真技術(shù)可以直接驅(qū)動結(jié)構(gòu)模型仿真，它在分析彈性與控制耦合類問題中具有突出的優(yōu)點，可以廣泛應(yīng)用到火箭總體設(shè)計中。比如：基于多體技術(shù)，可以直接實現(xiàn)控制-載荷一體化仿真，直接輸出有控條件下全箭不同部段的飛行載荷，有效解決傳統(tǒng)設(shè)計中，控制與載荷專業(yè)的模型與計算分離、參數(shù)包絡(luò)傳遞、條件重復(fù)考慮等因素帶來的結(jié)果保守類問題。又比如針對火箭豎立在發(fā)射臺上從點火到起飛的全過程，或者針對單臺發(fā)動機在飛行中出現(xiàn)推力脈動的現(xiàn)象，采用多體技術(shù)都能很好的實現(xiàn)仿真模擬，在新一代火箭設(shè)計中完成的相關(guān)工作很好的起到降低飛行風(fēng)險的作用。

多體動力學(xué)虛擬樣機仿真方法相當(dāng)大的程度上規(guī)避了傳統(tǒng)上完全以“代數(shù)-微分”方程描述為特色的建模與仿真方法的缺陷，是一種完全創(chuàng)新的方法，尤其適合對火箭結(jié)構(gòu)動力學(xué)特性與控制出現(xiàn)深度交叉耦合問題的開展分析。基于多體仿真方法，可以開展運載火箭總體設(shè)計當(dāng)中涉及到的彈道、控制、載荷、分離、POGO等多專業(yè)以及跨專業(yè)的一體化仿真[20]分析。可以預(yù)計，多體虛擬樣機仿真是相關(guān)航天器總體設(shè)計非常重要的技術(shù)發(fā)展方向。