空天飛行器返回滑翔段在線制導方法

周宏宇，王小剛，趙亞麗，崔乃剛

(1.哈爾濱工業大學航天學院，哈爾濱 150001；2.北京航天晨信科技有限公司，北京 102308)

0 引 言

隨著航天技術的快速發展和航天活動的多元化與頻繁化，航天發射的經濟性和靈活性愈發重要；在此背景下，可完全重復使用的空天往返飛行器應運而生。不同于運載火箭和航天飛機，空天飛行器采用多種動力模式入軌，上下兩級均有自主返回能力，在靈活性和經濟性上更具優勢，已成為各航天強國的研究熱點[1-4]。美國近年來完成了多次空天飛行器相關試驗[5-6]，印度于2016年完成了可重復使用驗證機首飛[7]，日本也于2019年制定了新一代空天飛行器研制計劃。

返回滑翔段是空天飛行器實現可重復使用的關鍵階段。由于再入速度高、滑翔距離遠，為實現安全返回，必須滿足熱環境、過載和擬平衡滑翔以及攻角和傾側角等控制約束[8]；同時還要滿足高度、速度、傾角、位置和航向等終端約束，從而順利過渡至末端能量管理段。此外，考慮初始返回狀態的不確定性和諸多干擾因素的影響，必須對滑翔段軌跡進行在線制導修正。

目前可用于空天飛行器返回滑翔段的制導方法包括標稱軌跡法[9-11]、預測校正法[12-14]以及在線優化法[15-16]等。其中文獻[9]給出了一種較為典型的標稱軌跡法，該方法事先設定攻角剖面并在飛行走廊中迭代傾側角，然后使用PID控制器跟蹤標稱攻角及傾側角指令。預測校正法通過在線求解終端狀態修正飛行指令，無需軌跡跟蹤器，抗干擾性更強。在線優化法通過反復計算最優軌跡修正飛行指令，能夠滿足多種飛行約束并保證飛行指標的最優性，具有很好的應用前景。

上述方法技術成熟、應用廣泛，但在空天飛行器應用中還需進一步研究與改進。首先，標稱軌跡法一般需要滿足小擾動假設并預設攻角形式，制約了任務的靈活性。預測校正法需在線計算終端偏差，但常見的基于數值解或解析解的預測方法難以兼顧計算量和計算精度。由于滑翔段航程遠、飛行環境復雜、非線性耦合強[17]，快速求解最優軌跡并非易事，故在線優化法需同時考慮最優性和收斂性的問題。為解決上述問題，諸多學者開始探索新的理論方法和技術途徑。基于滑模控制理論，文獻[18]設計了一種能夠克服大偏差的自適應軌跡跟蹤器。文獻[19]設計了一種改進型擾動觀測器，提高了標稱高度和速度剖面的跟蹤精度。文獻[20]采用反饋線性化理論，基于高低角和方位角信息實現了終端速度的快速預測。文獻[21]提出了一種快速優化算法，保證了最優軌跡的在線求解效率。同時一些混合方法正不斷涌現，如將標稱軌跡法和在線優化法結合，從而實現制導精度和計算量的最佳平衡。

針對滑翔軌跡在線重構需求，考慮氣動、約束、軌跡和指標間的復雜耦合關系[22]，從提高在線求解效率出發，設計了一種新的滑翔段飛行剖面。推導了滑翔段運動狀態、過程約束和性能指標的解析表達式，降低了優化問題的求解難度。在此基礎上提出了一種雙層在線制導方法：內層實時重構飛行剖面并借助解析解控制終端速度；外層使用混合優化算法優化飛行剖面，滿足過程約束的同時降低過載需求。該方法無需事先計算攻角與傾側角，無需設計軌跡跟蹤器，無需在線積分預測終端狀態，能夠自動滿足多種約束條件并保證軌跡的最優性。數學仿真驗證了方法的正確性和有效性；在非標稱狀態下，終端狀態相對偏差小于3%。

1 返回滑翔段運動數學模型

考慮地球自轉，空天飛行器在返回滑翔段中的運動方程如下：

(1)

式中：V為速度，γ為飛行路徑角，r為質心到地心的距離，ψ為航向角，θ為經度，φ為地心緯度；m為質量，D為阻力，L為升力，σ為傾側角，g為地球引力加速度，ωe為地球自轉角速度。

阻力和升力的計算方式為：

(2)

式中：cD和cL分別為阻力系數和升力系數，Sref為飛行器特征面積，q=ρV2/2為飛行動壓，其中ρ為大氣密度，可采用指數函數計算：

ρ=ρ0exp(-βh)

(3)

式中：β=1.41×10-4m-1與ρ0=1.225 kg/m3為常系數；h=r-Re為飛行高度，其中Re為地球平均半徑。

設氣動系數按如下規律變化：

(4)

式中：cD0,cL0,β1,β2,β3,β4為給定參數，α為攻角。

定義當前位置與終端位置間的航程為剩余航程，記為RL，則有：

(5)

式中：μL為剩余航程對應的地心航程角，θT和φT表示終端位置；ζ=ψw-ψ為航向偏差，其中ψw為期望航向角，計算方式如下：

(6)

空天飛行器在返回滑翔段中必須滿足諸多約束條件。為保證順利交班，設終端約束如下：

Φf=[hf,γf,Vf,RLf,ζf]T-[hc,γc,Vc,0,0]T=0

(7)

式中：下標“f”表示實際終端狀態，下標“c”表示期望終端狀態。

同時，設置過程約束如下：

(8)

式中：下標“max”表示該過程變量允許的最大值，NL=L/(mg)為速度坐標系下的法向過載，qr為駐點熱流。對于空天飛行器，熱流的計算方式如下：

(9)

式中：RN為駐點曲率半徑，取為0.08 m。

此外，滑翔段還應滿足擬平衡滑翔條件，具體表示為如下形式：

(10)

2 返回滑翔段飛行剖面設計

2.1 縱向剖面設計

設計飛行高度為剩余航程的函數：

(11)

式中：ai(i=0,1,…,n)為未知系數。取n=5。

1)攻角確定

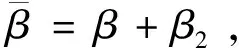
(12)

(13)

其中

(14)

根據式(1)和(2)，式(12)和(13)可表示為：

(15)

(16)

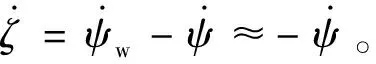
(17)

定義：

(18)

(19)

(20)

因此飛行剖面上各處的升力為：

(21)

注1.式中令ψw=arccos(Kw)，結合式可得：

(22)

2)剖面確定

由于n=5，需建立六個方程來求解F(RL)中的系數a0～a5。由于初始和終端高度已知，由式(11)可得：

(23)

式中：下標“0”表示滑翔段初始運動狀態。同時根據初始和終端飛行路徑角，由式(12)和(15)可得：

(24)

(25)

假設cosζ≈1，式(24)和(25)可改寫為：

(26)

(27)

定義：

(28)

類似于式(23)，可以得到另外兩個方程：

(29)

式中：h1和h2分別為剩余航程2/3和1/3處的高度值。定義剖面設計變量為uh=[h1,h2]T，因此只需兩個參數便能夠由式(23)～(29)求出a0～a5。

最后，給出剖面設計的性能指標函數。由式(21)可知，升力由f″(RL)決定；因此在滿足約束條件的前提下，若能使|f″(RL)|盡量小，則需用過載和攻角會更小。因此設計性能指標如下：

minJglide=max(|f″(RL)|)

(30)

2.2 側向剖面設計

設計傾側角為航向角偏差的函數：

(31)

式中：為ζm為給定正數，kσ為待定正數；設t0為傾側角翻轉時刻，則Δt=t-t0且σ0=σ(t0)。當t=t0時，σ=σ0；當t足夠大時，σ由航向偏差ζ決定。

(32)

定義Kσ=ζσmax/ζm-σ0，考慮到e-kσΔt≤1：

(33)

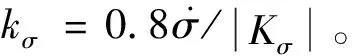
2.3 滑翔段解析解推導

2.3.1運動狀態的解析解

由于高度已定義為剩余航程的函數，以剩余航程為自變量，滑翔段高度的解析解即式(11)。

設cosζ≈1，cosγ≈1和sinγ≈γ；根據式(1)、(5)和(12)可得飛行路徑角的解析解為：

(34)

為求得速度的解析解，由動力學方程可得：

(35)

滑翔段中阻力通常遠大于引力沿速度方向的分量，因此式(35)可改寫為：

(36)

定義τD=cD0Srefρ0/(2m)，則有：

(37)

由式(11)、(34)和(37)可得：

(38)

對上式兩端積分得：

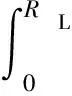
(39)

式中：CV為積分常數。定義：

(40)

因此滑翔段速度的解析解為：

V=[τDy(RL)+CV]-1/β1

(41)

由于RL0對應V0，可得CV=V0-β1-τDy(RL0)。同時由于RLf=0，故y(RLf)=0。因此終端速度為：

(42)

2.3.2過程約束和性能指標的解析解

根據式(41)，動壓的解析表達式為：

(43)

同時，駐點熱流的解析解為：

(44)

式中：ks=9.98×10-7，此時qr的單位為W/m2。

設cosζ=cosγ=1，則升力的解析解為：

(45)

因此法向過載的解析表達式為：

(46)

欲求性能指標即|f″(RL)|的極值，令f?(RL)=0；由式(13)可得：

(47)

其中

(48)

求解方程F2(RL)G1-2G2=0，便可得到f(RL)二階導數的極值，進而求出性能指標函數Jglide。

3 返回滑翔段在線制導算法

3.1 在線制導方法

通過設計縱向剖面和側向過載，終端高度、飛行路徑角、剩余航程和滑翔偏差得以自動滿足；而式表明終端速度是剩余航程的函數，因此可通過控制橫向機動改變剩余航程的變化率，使剩余航程匹配期望的終端速度。

通過設計路徑點來改變剩余航程。如圖1所示；其中p1為當前位置，p2為路徑點，p3為目標點。R12為p1p2間的航程，R23為p2p3間的航程，R13為p1p3間的航程。為滿足終端速度約束Vfc，由式(40)和(42)可得剩余航程應滿足：

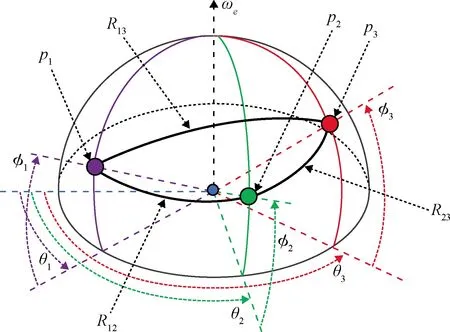
圖1 剩余航程控制方法

(49)

記方程(49)的解為RLw，則路徑點p2的選擇必須滿足R12+R23=RLw。參考式可得：

(50)

式中：θ2和φ2為路徑點p2的經緯度，ψ12為指向p2的期望航向角。

令R12=R23=RLw/2，由球面三角形定理可得：

(51)

式中：ψ13表示經過p2后指向目標點的期望航向角。因此，路徑點p2的位置為：

(52)

設從起點到當前位置飛過的航程為Rcov，制導周期為ΔRcov；在線制導方法具體如下所示：

1)路徑點更新

每五個周期(5ΔRcov)更新一次期望剩余航程RLw和路徑點p2；

2)剖面優化計算

每四個周期(4ΔRcov)計算一次uh=[h1,h2]T的最優值，使指標Jguide達到最小；否則uh的值不變；

3)剖面在線重構

每一個周期(ΔRcov)根據uh和當前運動狀態，由式(23)～(29)更新多項式F(RL)的系數a0～a5；

4)分別由式(21)和(31)計算攻角和傾側角；

5)更新參數τD；

6)積分動力學方程更新運動狀態；

7)返回步驟1)。

步驟1)是為了修正終端速度。步驟2)是為了更新剖面重構基準uh=[h1,h2]T，修正速度解析值與真實值間的偏差，滿足過程約束并保證軌跡的最優性。步驟3)是為了重構飛行剖面，從而滿足終端高度、位置和飛行路徑角約束。

3.2 混合優化方法

上述在線滑翔剖面優化問題實際上是一個含有五個過程(不等式)約束的雙參數尋優問題。只含不等式約束的優化問題可通過罰函數法轉化為無約束優化問題：

(53)

式中：rΦ為罰因子，NΦ為不等式約束的數量。上述無約束優化問題可采用CGM求解。基本CGM如下：

xl+1=xl+αldl

(54)

(55)

式中：αl,dl和βl分別為搜索步長、搜索方向和搜索因子；x=Uh=[h1,h2]T為優化變量，l為迭代次數；Gl為函數Jnew關于xl的梯度，可采用差分法求得。

標準CGM中的搜索步長為單調遞減，在迭代后期計算效率較低；因此按如下方式選取步長αl：

(56)

式中：δ1∈(0,1/2]和δ2∈(δ1,1)為預設常數。

為避免計算變量βl，將式(55)第二項改寫為：

dl=-QlGl,l>0

(57)

式中：Ql為二維方陣。定義sl=dl-dl-1,zl=Gl-Gl-1以及二維單位方陣I2，則Ql可按如下方式計算：

(58)

改進后的CGM如下：

1)令迭代次數l=0，初始化x0；

2)由式(55)第一項和式(57)確定搜索方向dl；

3)由式(56)確定搜索步長αl；

(1)給定αl的值，求出xl+1以及相應的性能指標梯度G(xl+1)；

(2)根據式(56)調整αl值，直至式(56)成立；

4)由式(54)計算xl+1；

5)根據xl+1判斷算法是否收斂：

(59)

式中：εj和εx為收斂精度。若滿足式(59)則終止迭代并輸出xl+1，否則l加1并返回步驟2)。

CGM在初值適合時收斂很快，而文獻[23]指出在慣性權重的值滿足一定條件時，PSO算法將快速收斂于近優解附近；因此，PSO[24]可作為CGM的初值求解器，由于初步計算h1和h2。

4 仿真分析

為驗證方法的正確性，建立表1所示仿真場景，其中初始航向角由式(6)求出，故初始航向偏差為零。設飛行器質量分別為6000 kg,5500 kg和5000 kg，特征面積分別為4.5 m2,4.0 m2和3.5 m2。

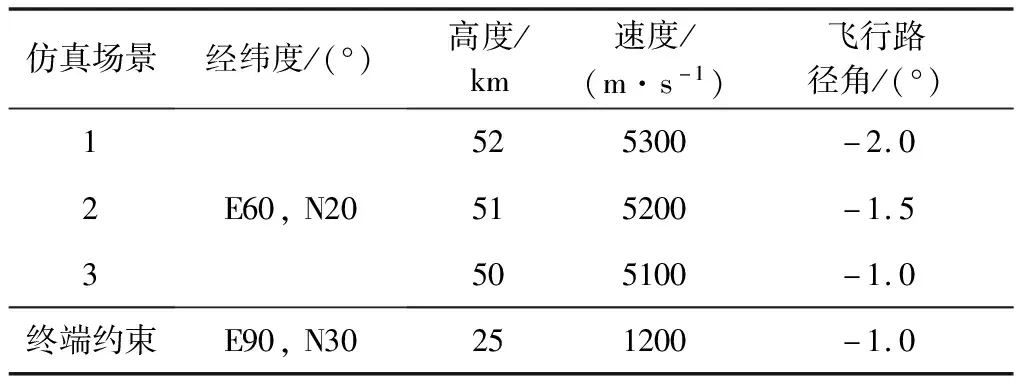
表1 仿真場景設定

首先不考慮干擾和偏差，得到仿真結果如圖2～圖7所示。圖2表明高度變化平緩，圖4表明飛行路徑角的絕對值始終小于2°(大多數時間小于1°)，滿足擬平衡滑翔條件和解析解中的前提假設。

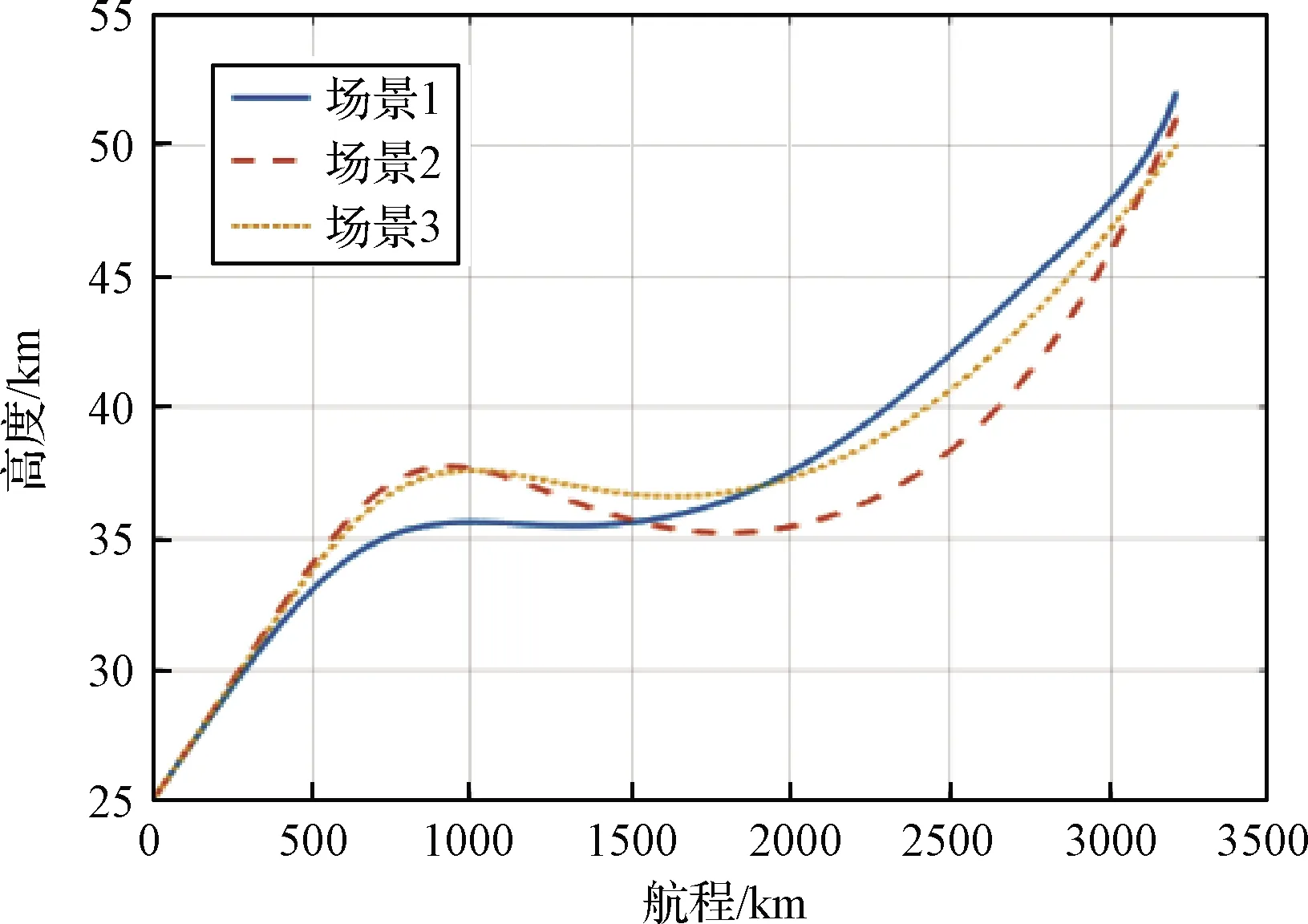
圖2 滑翔段飛行剖面

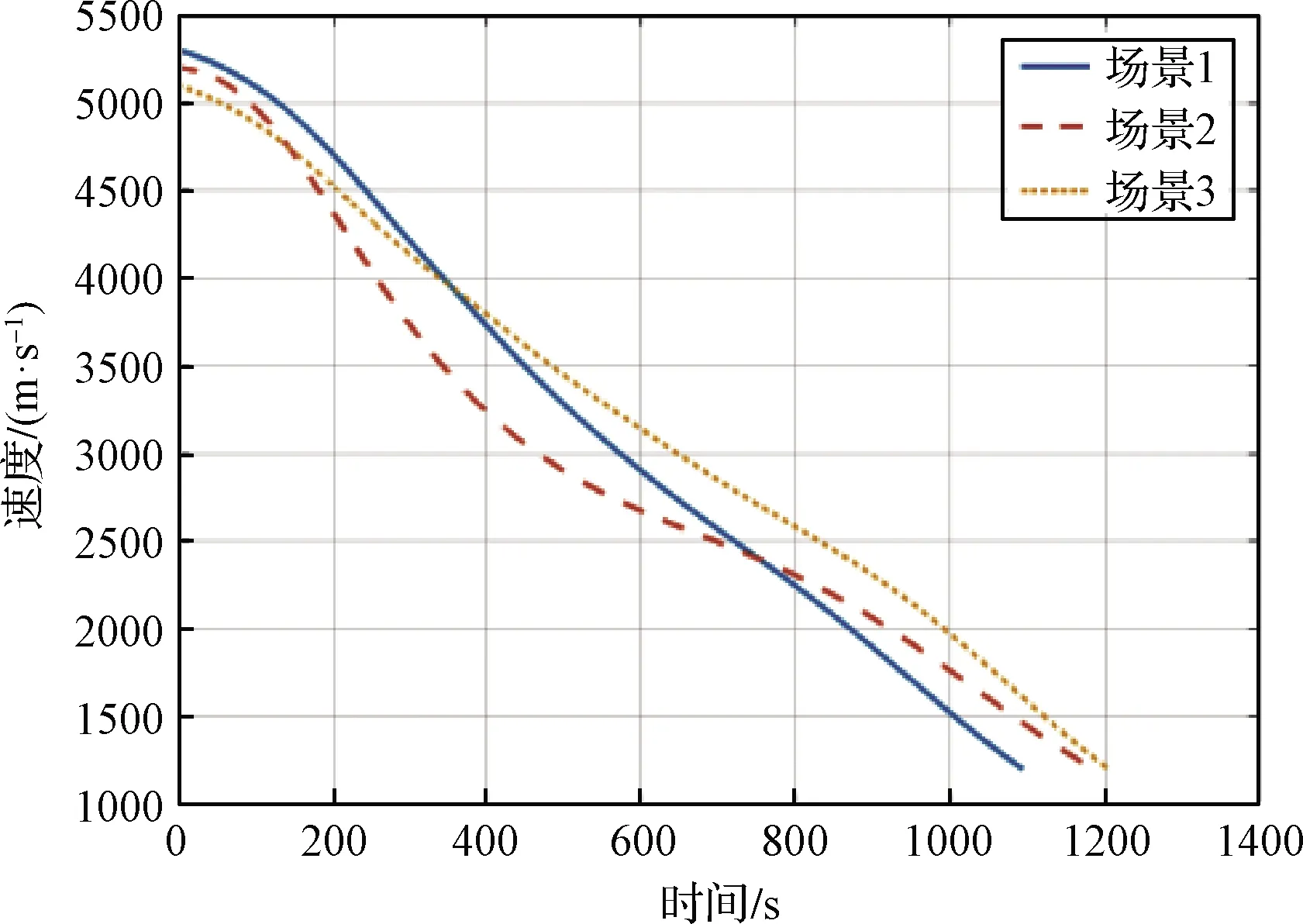
圖3 飛行速度隨時間變化情況

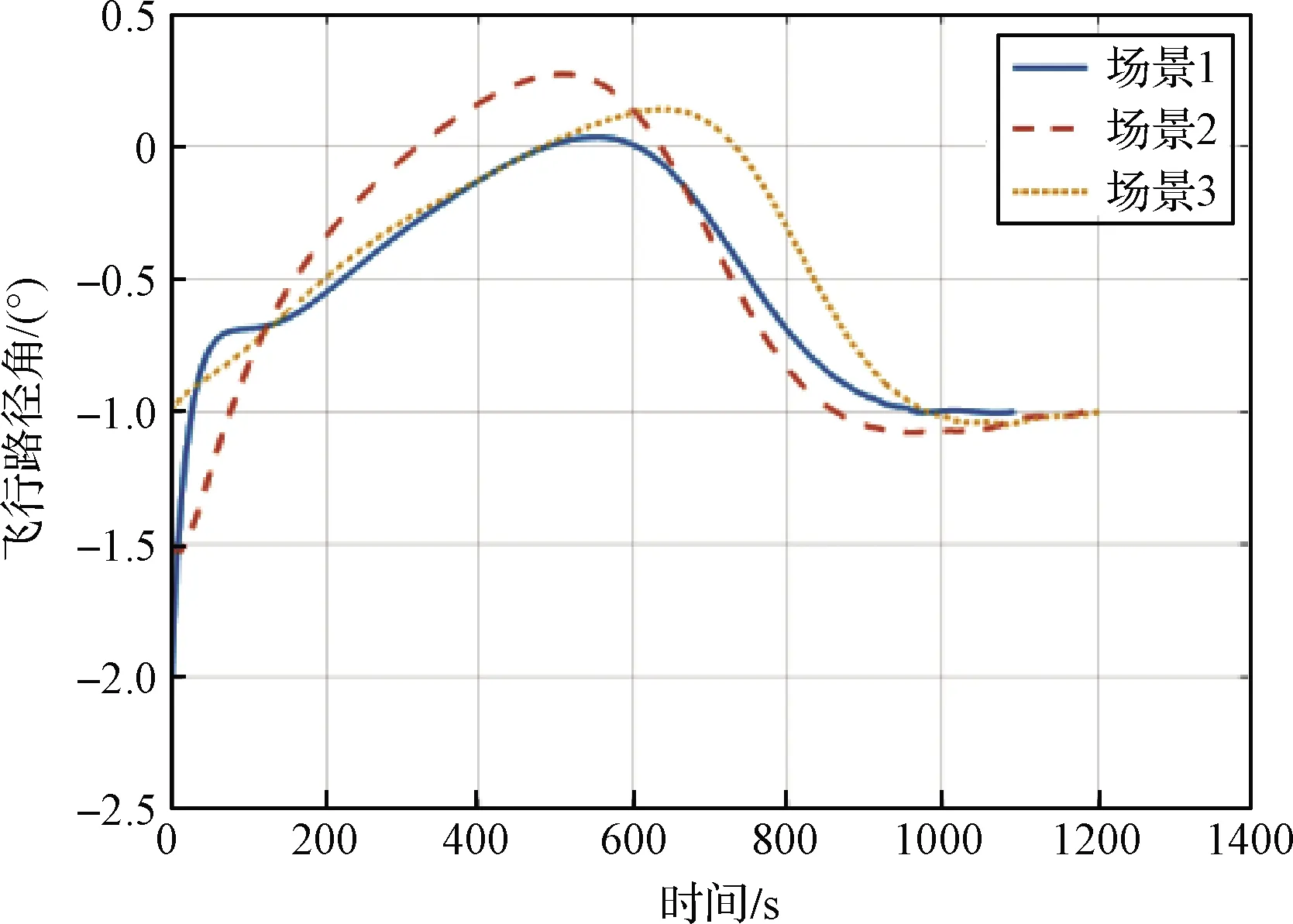
圖4 飛行路徑角隨時間變化情況

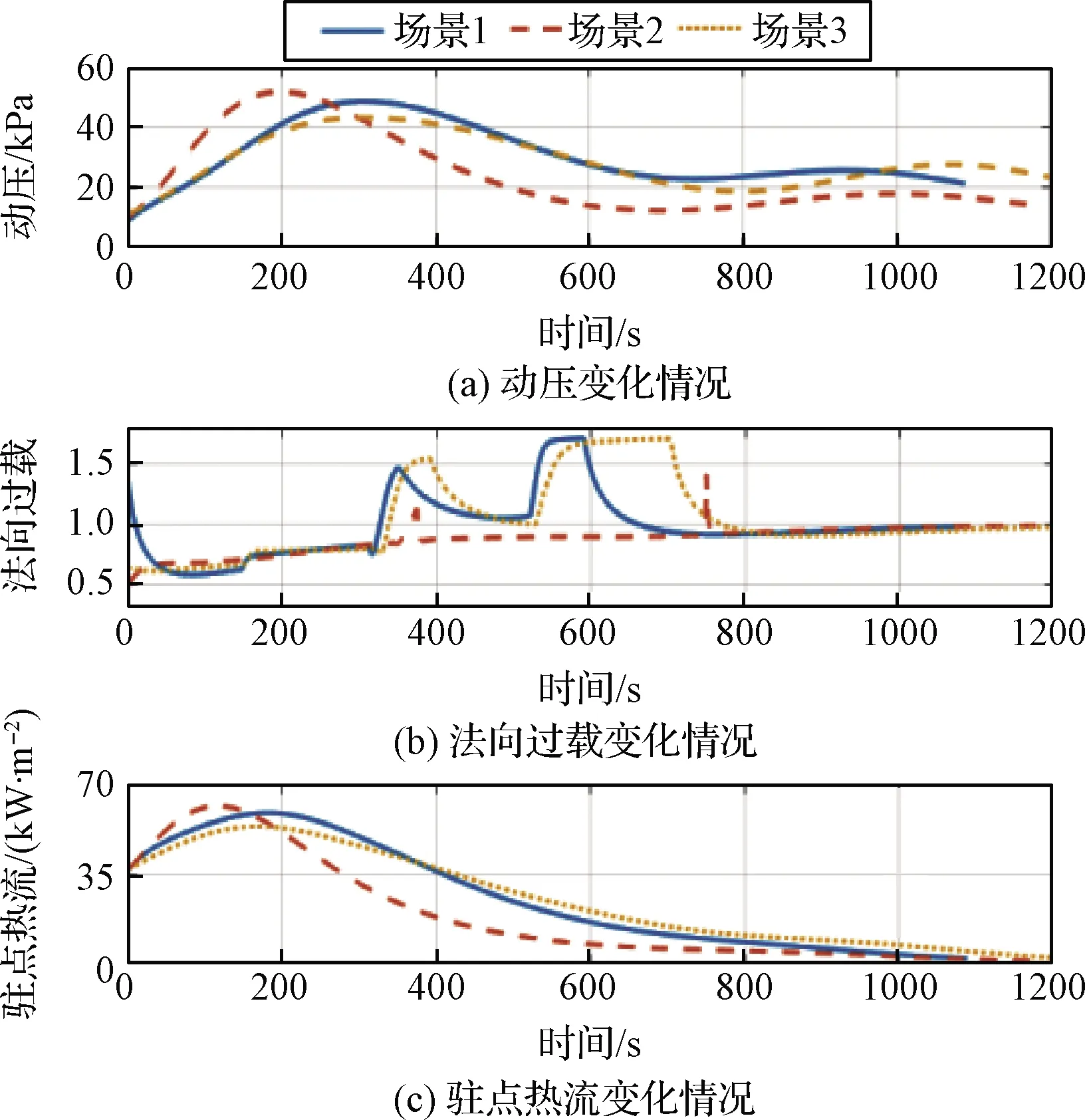
圖5 過程約束隨時間變化情況

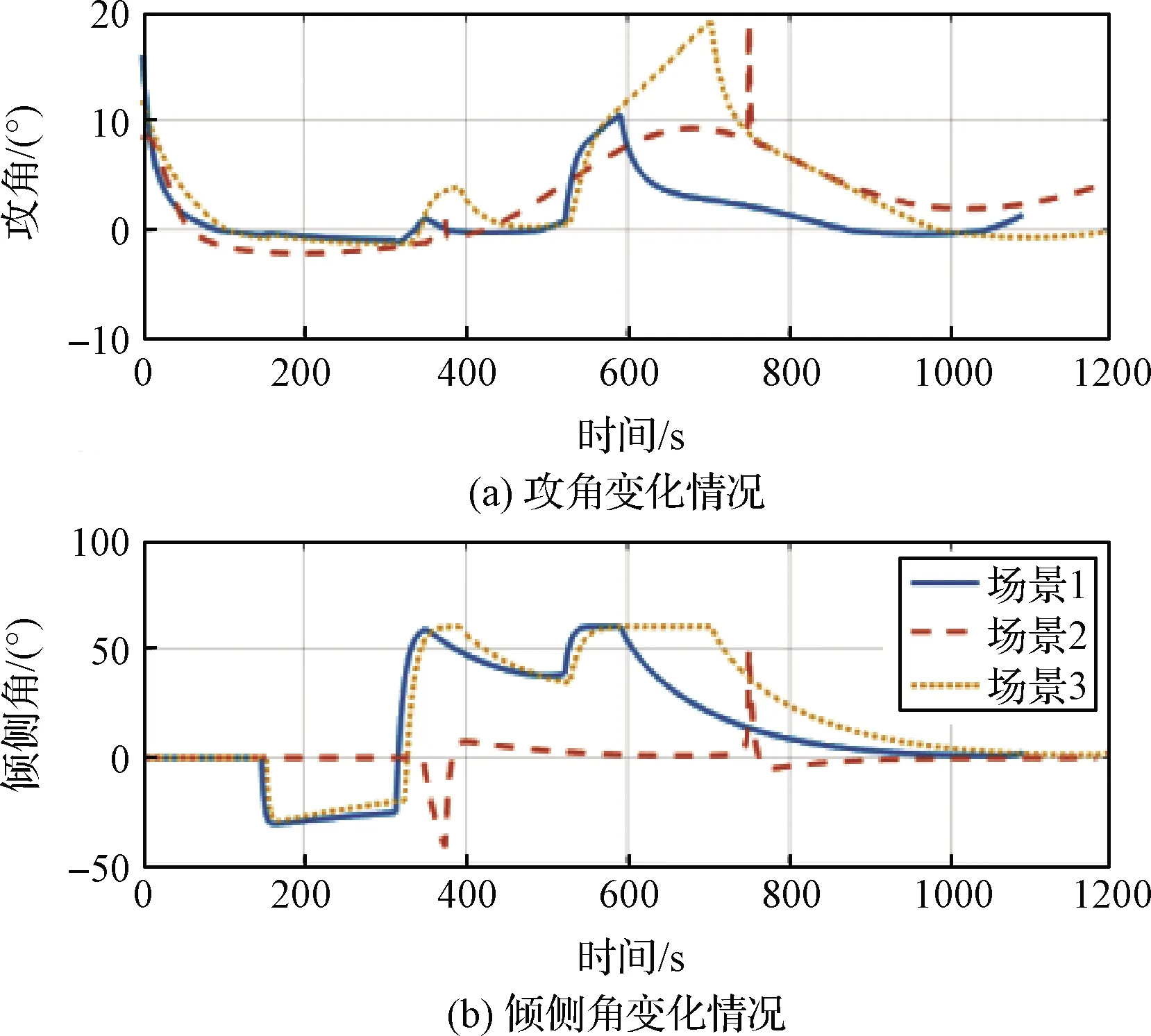
圖6 飛行指令隨時間變化情況

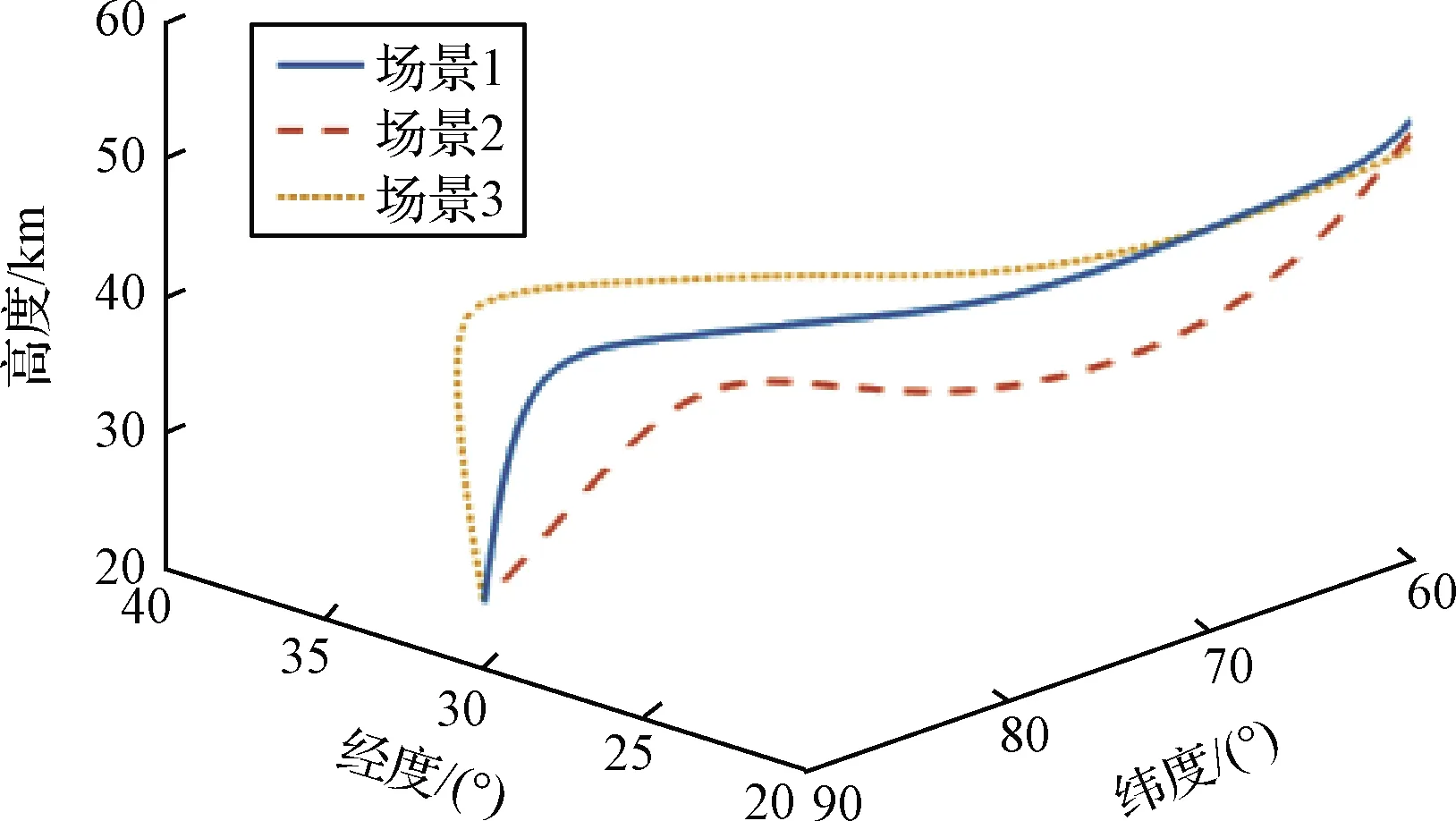
圖7 三維飛行軌跡

由于在線搜索剖面設計變量時使用了大量解析表達式，即使需要計算約20×15=300次性能指標，PSO也能很快得到初值。以場景1中首次(零時刻)優化計算為例，在東芝L001筆記本電腦(雙核4 GB內存、英特爾酷睿i3 M330/2.13 GHz處理器)上基于MATLAB 2016a執行混合優化算法，具體計算過程如圖8所示。

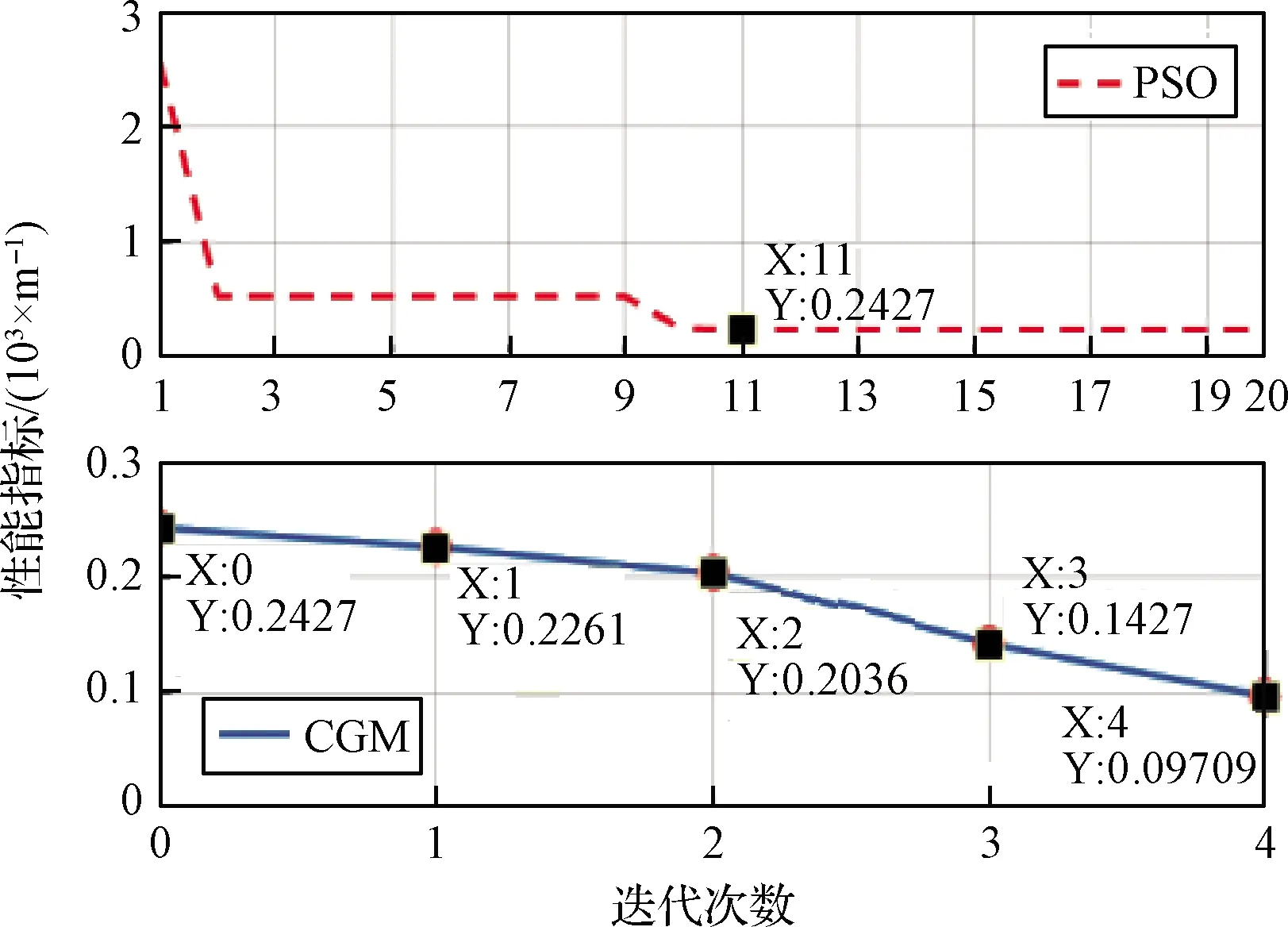
圖8 混合優化算法計算過程

由于上述滑翔段剖面設計方法能夠自動滿足終端高度、飛行路徑角和位置約束，在此僅關注終端速度偏差；如圖3所示，三種場景下，終端速度偏差分別為23.25 m/s、20.98 m/s和14.31 m/s；相對誤差分別為1.94%、1.95%和1.19%。

圖5表明各項過程約束均得到滿足。圖6表明攻角指令十分平滑。由于攻角源于函數F(RL)的二階導，因此攻角變化率是連續的，同時傾側角指令也是連續光滑，這對控制系統是很有利的。在路徑點處，期望航向的變化導致了側向過載方向的改變，因此傾側角會出現突變，同時攻角也會出現突變；但在傾側角計算過程中已經考慮了精度變化率約束，因此路徑點處的飛行指令變化幅度滿足控制系統的能力約束。同時，在滑翔段的絕大多數時間里，攻角和傾側角指令均是平滑連續的。

圖8中，PSO用時0.2 s(優化結果為h1=36.5 km，h2=35.3 km)，CGM用時0.06 s(迭代4次后收斂，結果為h1=38.4 km，h2=35.6 km)，說明基于解析解的在線優化算法滿足計算效率要求。另外，圖8表明PSO算法在進化第11代時已經收斂，說明可以用更少的進化代數或粒子數完成初值計算。但PSO具有隨機性，故不宜采用過少的進化代數或粒子數。

其次考慮干擾因素，設置服從均勻分布的滑翔段干擾因素如表2所示。以表1中的場景1為例進行500次蒙特卡洛打靶仿真，結果見圖9～圖12。

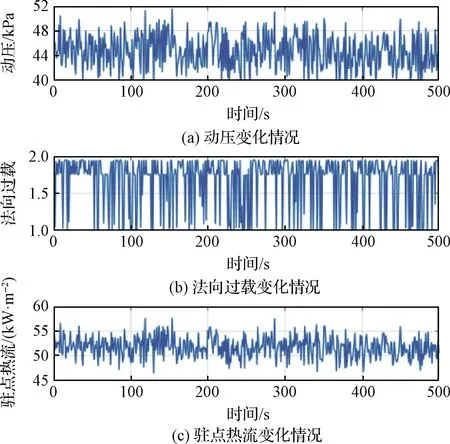
圖12 過程約束滿足情況

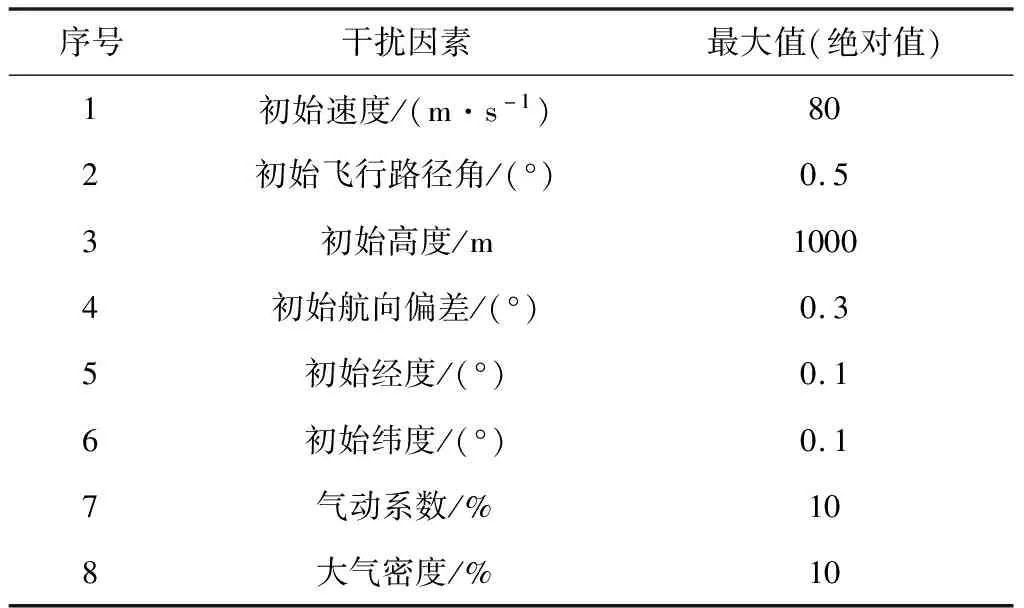
表2 滑翔段干擾因素

如圖9所示，終端速度偏差的絕對值在500次仿真中的最大值為34.98 m/s(相對誤差2.91%)，平均值為20.34 m/s(相對誤差1.69%)。

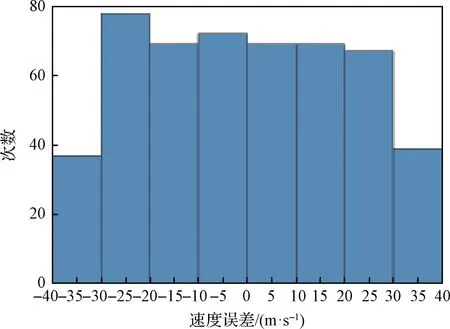
圖9 終端速度偏差直方圖

圖10和圖11表明，終端約束在非標稱條件下依然能夠得到滿足，同時飛行路徑角值保持在0°附近，滿足擬平衡滑翔條件和解析解中的前提假設。圖12給出了單次仿真中各過程變量的最大值，可以看出在500次仿真中，過程約束均得到滿足。

圖10 滑翔段飛行剖面

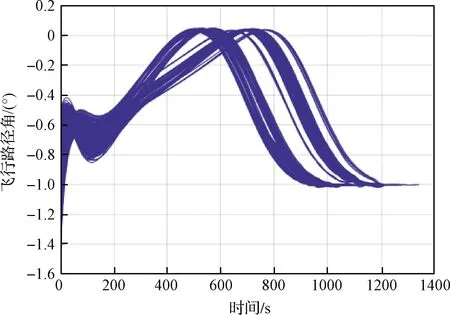
圖11 飛行路徑角隨時間變化情況

最后指出，仿真中取更新周期ΔRcov=50 km；由表1中的初始速度可知，ΔRcov對應的飛行時間大于10 s。因此，路徑點更新周期(5ΔRcov)大于50 s，而飛行剖面優化周期(4ΔRcov)大于40 s。基于上述剖面設計方法和解析解，該更新周期在仿真中足夠完成在線剖面優化以及三維滑翔軌跡重構。

5 結 論

面向未來新一代空天往返可重復使用飛行器，針對返回滑翔段在線制導問題展開深入研究，取得的主要成果如下：

1)推導了滑翔段高精度解析解，得到了運動狀態、過程約束和性能指標的解析表達式；

2)設計了一種新的雙層在線制導方法；該方法無需事先計算攻角或傾側角，無需設計高精度軌跡跟蹤器，無需在線積分預測終端狀態，同時能夠保證軌跡的最優性；

3)提出了一種混合優化算法，將PSO與改進CGM相結合，提高了優化問題的求解效率；

4)攻角指令的一階導即變化率連續，這對控制系統是很有利的；同時攻角解算中考慮了地球自轉的影響，制導精度得以保證。