一種天文導航信息導引的星間鏈路自主定軌算法

林 夏，林寶軍,5，劉迎春，白 濤，武國強

(1.上海微小衛星工程中心，上海 201203；2.中國科學院微小衛星創新研究院，上海 201203；3.中國科學院空天信息創新研究院，北京 100094；4.中國科學院大學計算機科學與技術學院，北京 100094；5.上海科技大學信息學院，上海 201210)

0 引 言

為提升導航精度及戰時自主運行能力，各衛星導航系統均開展了衛星自主導航算法的研究工作。美國GPS衛星系統最先啟動了此類研究。1984年，Ananda等[1]首先提出了不依賴地面監測系統支持，僅利用星間測距信息的導航衛星自主導航技術，并將該自主導航技術成功應用于GPS BLOCK IIR衛星中。GPS BLOCK IIR衛星通過星間雙向測距信息對長期預報星歷的校正，在75天內，用戶測距誤差小于3 m[2]。

新一代北斗全球導航衛星系統也引入了星間鏈路測量體制，并開展了星間鏈路自主導航試驗。與GPS BLOCK IIR衛星采用的UHF頻段星間鏈路不同，北斗全球導航衛星采用了測距精度更高，通信能力更強的Ka頻段星間鏈路[3]。經在軌試驗評估，Ka鏈路星間測距精度優于10 cm，通信速率可達50～100 kbps。且通過相控陣技術，衛星可實現快速的星間Ka鏈路切換建鏈，5 min周期內一般可完成與14顆他星的建鏈[4]。目前北斗衛星自主導航技術仍處于整網聯試階段，還未公布其自主導航精度。與此同時，北斗衛星也已開展了激光星間鏈路的相關研究，并完成了基于激光星間鏈路的北斗衛星組網方案論證工作[5]，力求進一步提升導航衛星軌道及時間同步精度。

對于星間鏈路自主導航算法，當前學者們集中于算法精度提升方法的研究，并取得了一定的成果[6-7]。其成果主要分為三類:1)為對星座整體旋轉問題抑制方法的研究。增加錨固站星地測量鏈路被證明為一種有效的克服慣性空間及地球固聯空間星座整體旋轉的方法[8-10]。文獻[11-12]也指出，基于天文信息約束也可使星座整體旋轉在慣性空間中得以抑制。2)對濾波處理策略的研究。相比于當前導航星座衛星使用的分布式濾波處理策略，集中式濾波處理方法可獲得更高的導航估計精度。文獻[13-14]分別提出了有效的可在星上應用的集中式處理方法。3)對鏈路測距誤差消除方法的研究。文獻[15-17]提出了相應的北斗衛星Ka鏈路系統誤差修正方法，有效地提高了衛星的鐘差及軌道精度。

為使導航衛星真正具備自主運行能力，除提升自主導航精度，使衛星具備自主播發高精度時空基準的能力外，還需使衛星具備長期穩定運行及故障恢復的能力。由于星間鏈路自主導航算法中的自主精密定軌算法為半自主定軌算法，穩定性較差，因而急需開展提升算法穩定運行能力的方法研究。但目前還未有成熟有效的解決方法。

具體而言，星間鏈路自主定軌算法并非為完全自主的衛星軌道確定算法。為確定衛星軌道信息，算法需首先完成星間測距及星間信息交換。因而，星座中有一顆衛星出現故障，整網衛星建鏈精度及自主定軌精度均將受到影響。星間鏈路定軌算法穩定性較差。再者，星間鏈路自主定軌算法也缺乏自主故障恢復的能力。衛星與他星建鏈需實時獲得自身軌道信息以調整鏈路指向，一旦衛星機動或衛星姿態失穩，星上軌道信息出現偏差，衛星鏈路將無法與他星對準建鏈。更為嚴重的是，由于無法通過建鏈獲取觀測信息修正軌道誤差，星間將無法自主恢復建鏈，星間鏈路自主定軌算法也將無法進行使用。

為解決上述問題，本文提出了一種基于天文導航信息導引的星間鏈路自主定軌算法，以提升星間鏈路定軌算法的穩定運行能力。首先，天文導航算法無需與外界進行信息交換，具有極高的穩定性與完全自主性。因而可利用天文導航算法的輸出軌道信息確定鏈路指向，使衛星與他星長期穩定建鏈，保證星間鏈路自主定軌算法長期穩定運行。再有，天文導航算法可在任意指向采集所需天文信息以獲得當前衛星軌道信息。因而，當衛星姿態失穩或由于軌道機動產生星上軌道信息偏差以致鏈路中斷時，天文導航可確定當前衛星軌道，使衛星與他星間重新建鏈。本文在天文導航算法中加入強跟蹤濾波算法，使天文導航算法快速收斂，以使星間鏈路自主定軌算法快速恢復建鏈。最后，天文導航算法可提供星間鏈路自主定軌算法的初始軌道參考信息，幫助星間鏈路自主定軌算法重啟運行時衛星軌道信息快速收斂，并擺脫對地面軌道上注的依賴。

1 天文導航及星間鏈路定軌算法原理

基于天文導航信息導引的星間鏈路自主定軌算法利用天文導航算法獲得的天文導航信息，為星間鏈路自主定軌算法提供星間鏈路建鏈指向及初始軌道信息，以提高星間鏈路自主定軌算法的穩定性與自主性。下面分別對兩導航算法原理進行介紹。

1.1 天文導航算法原理

本文采用的基于星光角距信息的天文導航算法是一種動力學導航算法。分別從預報模型，觀測模型與濾波模型三部分對算法作以介紹。

1)預報模型

如式(1)所示，衛星動力學軌道預報模型可由牛頓二體定律得到。

(1)

式中:rsat為衛星慣性系位置向量，vsat為衛星慣性系速度向量，asat為衛星慣性系加速度向量。wrsat為衛星位置向量過程噪聲信息，wvsat為衛星速度向量過程噪聲信息。wrsat，wvsat均可視為零均值白噪聲向量。

由于導航衛星為中高軌道衛星，因而對于預報模型中衛星加速度向量asat的計算，主要考慮4×4階地球非球形引力，日月引力，太陽光壓攝動力引起的衛星加速度變化。

2)觀測模型

天文導航算法通過采集星敏感器與地球敏感器的敏感信息，形成星光角距觀測信息，從而形成天文導航算法觀測量及觀測方程，其具體步驟如下所示。

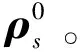
(2)

式中:fs是星敏光學焦距。

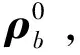
(3)

(4)

式中:Rbh是地敏坐標系到衛星本體系的轉換矩陣。

(5)

再者，星光角距觀測量as還可通過式(6)表示

(6)

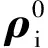
(7)

式中:(?,δ)是慣性坐標系衛星的恒星天球坐標。通過星圖識別和星敏感器中內置的恒星星歷，該恒星的天球坐標可精確得到。

(8)

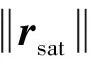
將式(8)代入式(6)，星敏感器與地球敏感器聯合自主導航算法的觀測方程即可通過式(9)表示

(9)

3)濾波模型

如式(9)所示，天文導航算法觀測方程為非線性方程。因而，在設計中，采用擴展卡爾曼濾波算法(EKF)對算法進行估計。

(10)

1.2 星間鏈路定軌算法原理

星間鏈路自主定軌算法分為分布式與集中式兩種處理方法，本文采用的為集中式處理方法。由于星間鏈路自主定軌算法預報模型與天文導航算法相同，因而本節僅對星間鏈路自主定軌算法的觀測模型及濾波模型作以介紹。

1)觀測模型

星間鏈路自主定軌算法是以星間雙向測距信息作為觀測量并構建觀測方程。算法觀測量及觀測方程形成方法如下。

衛星星間雙向測距原始信息可表示為

(11)

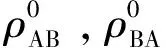
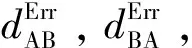
(12)

并且，依據算法觀測量與算法待求衛星位置，速度信息關系，可得到如式(13)所示觀測方程。

(13)

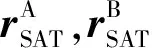
2)濾波模型

與天文導航算法相似，星間鏈路自主定軌算法也采用EKF算法對衛星軌道信息進行估計。

因而，算法狀態向量調整為A，B兩星位置速度信息的一階誤差量。算法觀測方程由式(13)調整為式(14)所示形式。

(14)

2 天文導航信息導引的星間鏈路自主定軌算法

本文提出的基于天文導航信息的導引方法使星間鏈路定軌算法具有自主穩定建鏈及故障恢復的能力，從而極大地提升了星間鏈路自主定軌算法的穩定運行能力。下面對基于天文信息的自主建鏈及故障恢復實現方法作以介紹。

2.1 基于天文導航信息的自主建鏈方法

對于星間鏈路自主定軌算法，單星定軌精度依賴于整網衛星交換信息精度，因而算法穩定性較差。星間鏈路建鏈需獲取衛星軌道信息，若直接引入星間鏈路自主定軌算法得到的軌道信息，其建鏈穩定性也將受到極大制約。針對此問題，本文提出了基于天文導航信息的自主建鏈方法。利用天文導航算法的高可靠性，使星間建鏈具有極高的穩定性。

結合星間鏈路建鏈原理，提出的基于天文導航信息的自主建鏈方法設計如下，具體流程如圖1所示。

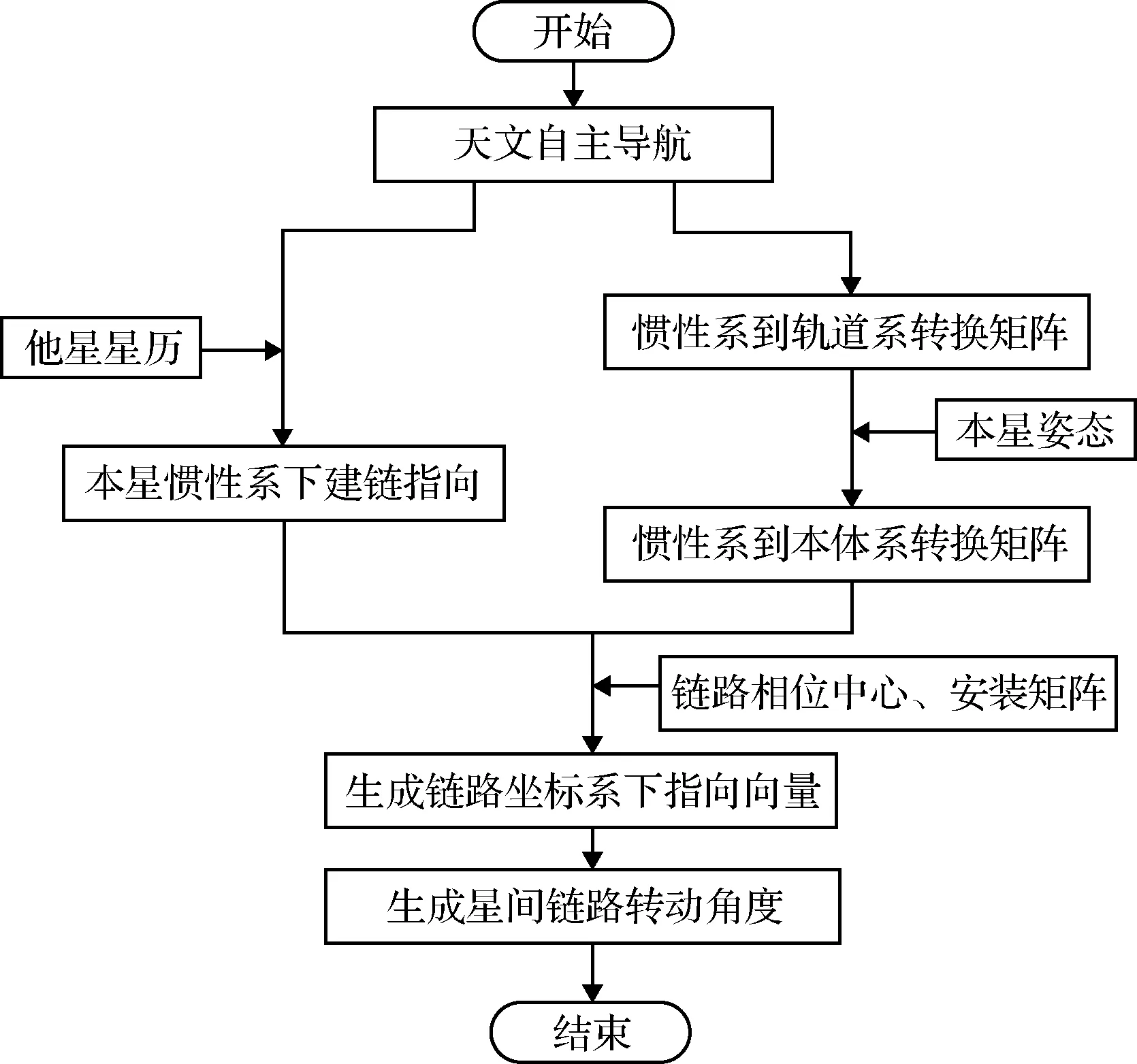
圖1 基于天文信息的自主建鏈方法流程圖

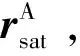
(15)

2)利用天文導航信息獲取慣性系到衛星軌道系轉換矩陣，方法如式(16)所述。并結合衛星姿態信息獲得衛星慣性系到本體系的轉換矩陣。方法如式(17)所述。

(16)

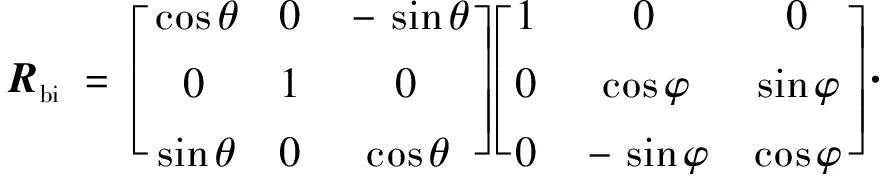
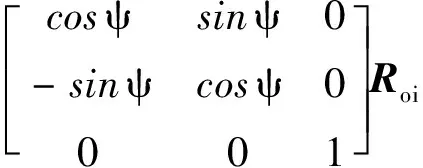
(17)

式中:θ，φ，ψ分別為衛星三軸姿態角信息，Roi,Rbi分別為慣性系到軌道系，慣性系到本體系的轉換矩陣。

3)根據已知的鏈路相位中心本體系坐標PLb，鏈路本體系下安裝矩陣RLb以及獲得的慣性系到本體系轉換矩陣Rbi，將慣性系下指向向量PAi轉換為鏈路坐標系下的建鏈指向向量表示PAL，方法如式(18)所示。

PAL=RLb(RbiPAi-PLb)

(18)

4)基于鏈路坐標系下的建鏈指向向量表示PAL，可最終計算出鏈路坐標系下的目標轉動角度，用于鏈路指向姿態調整，方法如式(19)(20)所示。

(19)

(20)

式中:PAL=(xAL,yAL,zAL)為建鏈指向向量的三軸坐標，(Ei,Az)為鏈路指向俯仰角與方位角。

根據以上四步，即可完成基于天文導航信息的衛星星間鏈路自主建鏈。

2.2 基于天文導航信息的強跟蹤自主建鏈恢復方法

當衛星采用星間鏈路定軌算法自主運行時，若衛星軌道機動或姿態失穩，衛星與他星的星間鏈路將會中斷。而當衛星軌道機動結束或衛星姿態恢復穩定后，由于實時衛星軌道信息無法獲取，星間鏈路無法重新建鏈，進而星間鏈路自主定軌算法無法恢復運行。本節提出了一種基于天文導航信息的強跟蹤自主建鏈恢復方法。利用天文導航的完全自主性與強跟蹤算法的快速收斂性，使鏈路中斷后的衛星快速獲得當前實時軌道信息，從而恢復建鏈使星間鏈路自主定軌算法恢復運行。同時在星間鏈路自主定軌算法重啟伊始，天文導航為鏈路定軌算法提供初始軌道信息，使鏈路定軌算法獲得初始基準快速穩定輸出。設計的自主建鏈恢復方法流程如圖2所示。

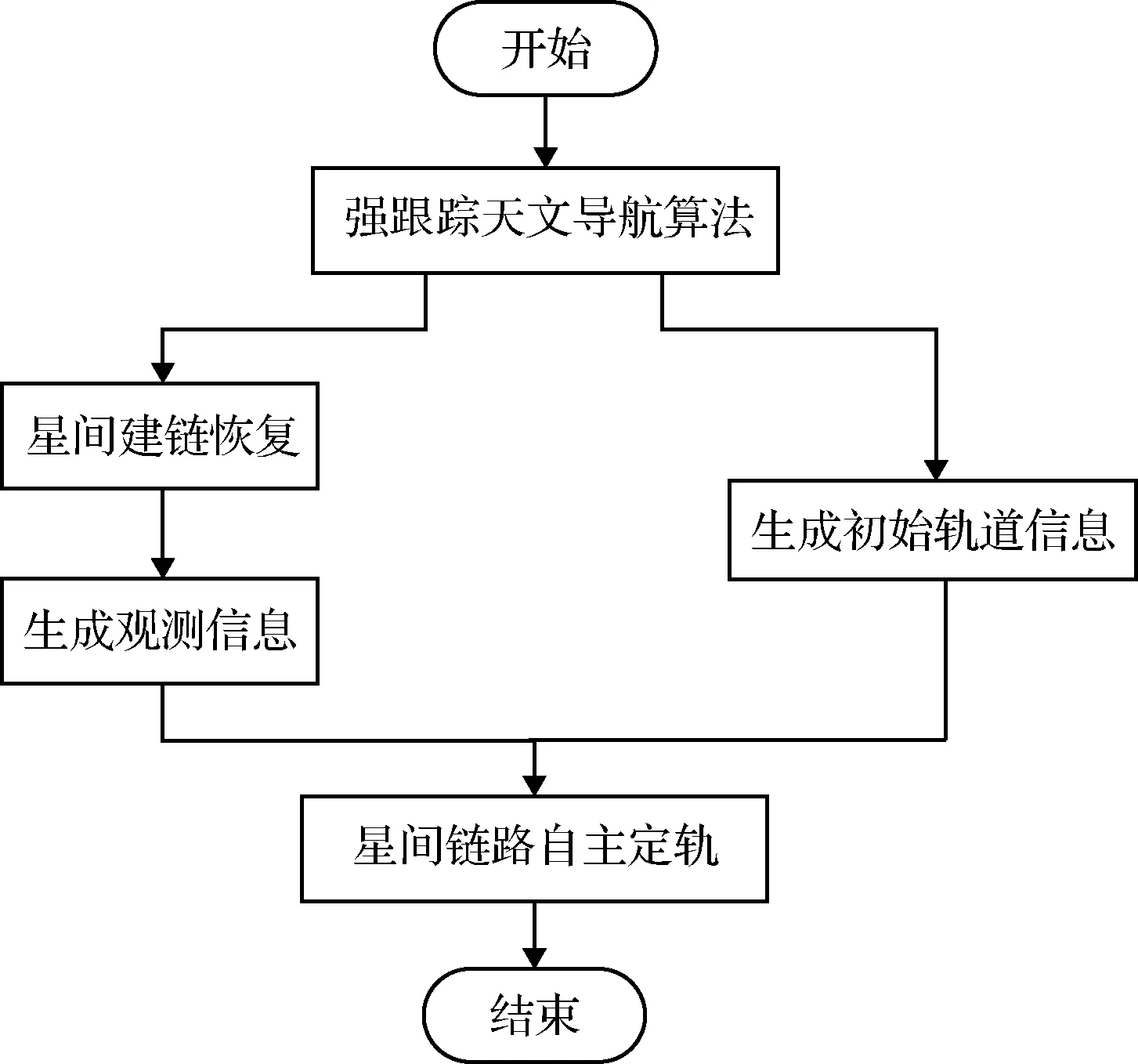
圖2 自主建鏈恢復方法流程圖

本文在傳統的天文導航算法中加入了強跟蹤濾波處理環節，以使衛星可在軌道信息丟失時快速確定自身軌道。強跟蹤濾波算法通過將次優漸消因子λ引入傳統EKF濾波算法的預報協方差陣Pk/k-1中，使濾波算法在狀態突變時仍能保持對真實狀態的跟蹤能力[19-20]。其引入方法如式(21)所示。

(21)

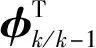
由于強跟蹤濾波器需滿足如式(22)所示條件，因而有如式(23)所示等式。

(22)

(23)

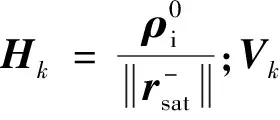
(24)

式中:β為遺忘因子，本文選取為β=0.95。

本文將次優漸消因子λ視為單重次因子。因而，依據式(23)，可利用式(25)計算得到λ

(25)

3 仿真分析

根據設計的基于天文導航信息導引的星間鏈路自主定軌算法，對基于天文導航信息的自主建鏈性能與基于天文導航信息的建鏈恢復能力進行仿真分析，仿真場景與仿真結果描述如下。

3.1 仿真場景建立

建立24顆MEO北斗星座衛星的仿真場景，星座內各衛星編號簡化為PRN01～PRN24。各衛星均采用偏航姿態飛行。各星標準軌道及標準姿態均由Satellite Kit Tools(STK)軟件生成。根據北斗衛星在軌測試評估結果，衛星預報軌道依據1.1節所述預報模型加入10%光壓誤差得到，衛星預報姿態在標準姿態基礎上，滾動，俯仰，偏航姿態分別加入0.02°，0.02°，0.04°誤差。

仿真場景中，利用PRN01星驗證本文設計的天文導航信息導引的星間鏈路自主定軌算法。對于天文導航算法，設置算法仿真周期為4 s，星敏感器三軸隨機噪聲為5″(3σ)，地球敏感器隨機噪聲為0.015°(3σ)，系統噪聲0.01°。對于星間測距導航算法，設置算法仿真周期為5 min，設定Ka鏈路坐標系安裝矩陣為單位陣，安裝位置坐標為(0，0，0.5)m，并且考慮地球遮擋，鏈路仰角、方位角死區等因素，建立鏈路規劃表，各星依據規劃表完成星間雙向測距。各星每周期平均與10顆他星建鏈，星間測距誤差均為0.1 m。

3.2 仿真結果分析

首先依據仿真場景對基于天文導航信息的星間鏈路建鏈穩定性進行評估。

根據天文導航算法仿真條件，經時長為2天的天文導航算法仿真，其導航精度如圖3所示。待算法穩定收斂后，其三軸最大位置精度分別為7270.1 m，6936.9 m，6753.9 m，三軸速度最大誤差分別為1.6205 m/s，1.0982 m/s，1.4526 m/s。算法誤差與文獻[21]所述在軌北斗衛星天文導航評估精度6000 m，速度精度1.5 m/s基本一致，即驗證了本文天文導航算法仿真結果的有效性。

圖3 穩定運行時天文導航算法導航精度圖

將天文導航算法得到的軌道信息引入本文設計的自主建鏈方法中，評估基于天文導航算法的衛星建鏈精度。經2天時長評估，其建鏈指向精度如圖4所示。在引入姿態誤差[0.02°，0.02°，0.04°]后，建鏈仰角指向誤差為0.042°，方位角指向精度誤差為 0.082°。因而，通過仿真分析可知，利用設計的基于天文信息的自主建鏈方法，星間建鏈可以保持高精度穩定。

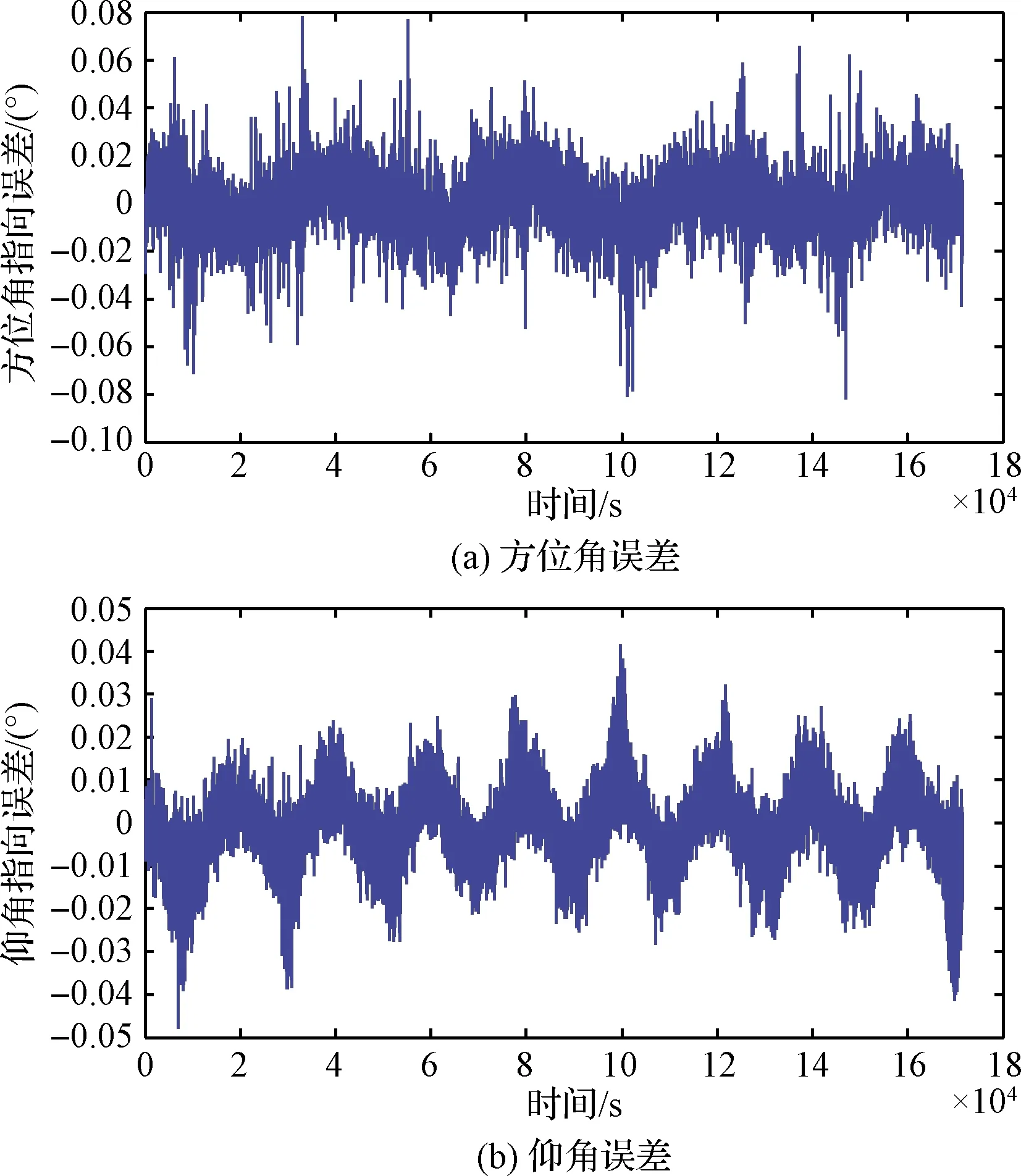
圖4 穩定運行時衛星星間鏈路指向精度

而后，對基于天文導航信息的強跟蹤自主建鏈恢復效果進行評估。

在平穩運行一段時間后，對衛星進行30 min的軌道機動，衛星受推力加速度為0.03 m/s2，以評估當出現姿態失穩，衛星機動等狀態突變后，天文導航算法的強跟蹤建鏈恢復能力。經2天時長的仿真，算法自主建鏈恢復效果如下所示。

當衛星軌道機動時，星上定軌精度快速下降。如圖5所示，軌道機動后，三軸軌道位置誤差可至[3.74,0.832,1.67]×105m，速度誤差可至[113.05,9.23,7.45]m/s。同時，受此軌道精度影響，建鏈指向精度也快速下降，如圖6所示，星間鏈路建鏈仰角指向誤差最大可達1.04°。依據此建鏈指向精度，衛星星間鏈路已無法與他星建鏈，因而星間鏈路自主定軌算法將無法運行。

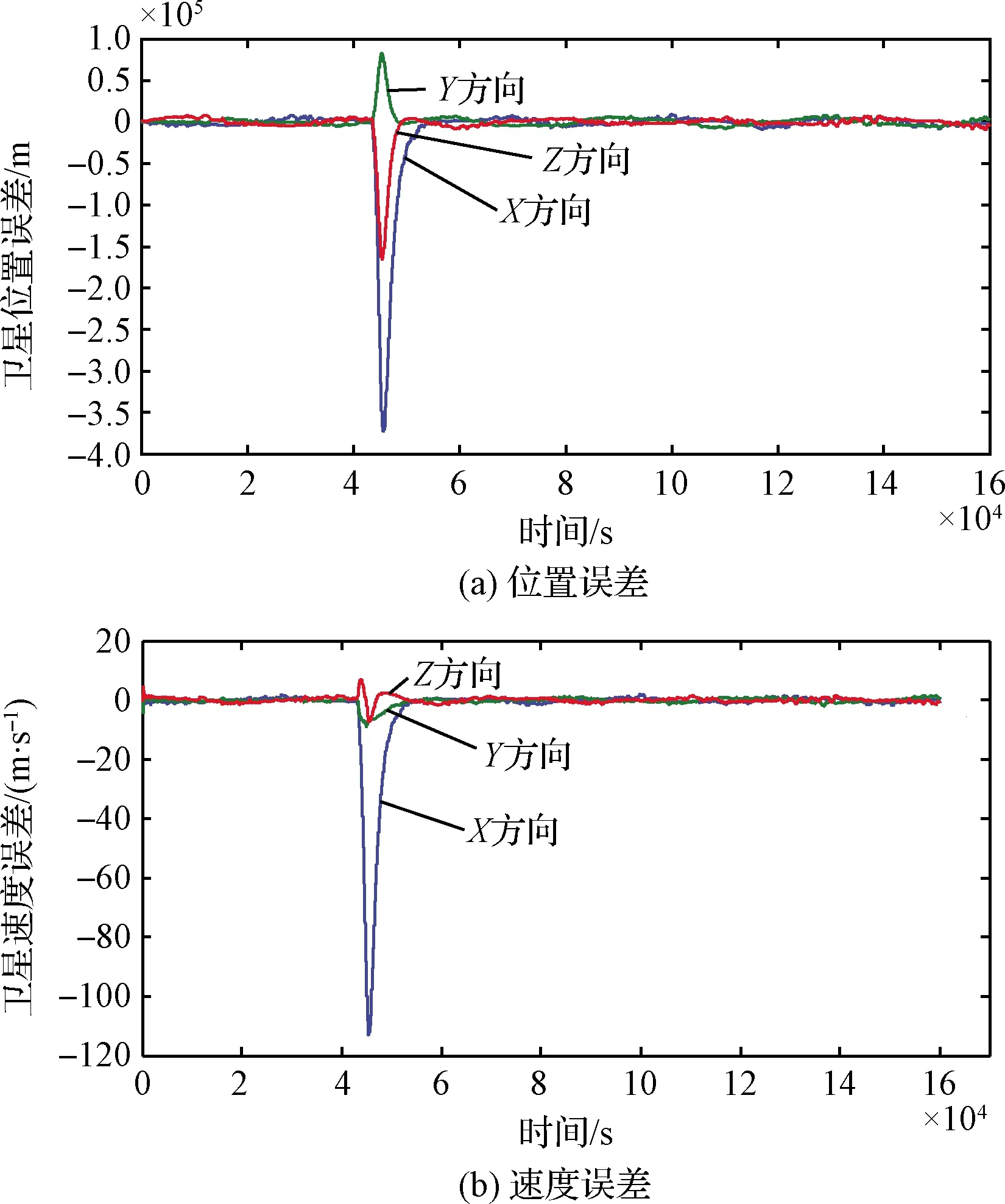
圖5 狀態突變時天文導航算法定軌精度

圖6 狀態突變時衛星星間鏈路指向精度

采用本文設計的基于天文導航信息的強跟蹤自主建鏈恢復方法，如圖5～6所示，軌道機動后的衛星定軌誤差，建鏈指向精度均快速收斂。其中建鏈指向仰角精度及方位角精度在軌道機動5000 s后即恢復至0.1°以內，可使星間鏈路重新恢復建鏈。

將收斂后的天文導航算法軌道信息作為初始軌道應用于星間鏈路自主定軌算法中，以評估建鏈恢復后星間鏈路自主定軌算法精度。當建鏈指向精度恢復至0.1°時，利用天文導航軌道信息作為星間鏈路自主定軌算法初始軌道(位置誤差為[1.9643,0.1114, 0.4478]×104m，速度誤差為[-5.2834,-1.6846,1.3775]m/s)，并重新啟動星間鏈路自主定軌算法，進行時長為30天的算法仿真。如圖7，PRN01星星間鏈路自主定軌算法經15次迭代后URE誤差收斂于3 m以內，并最終誤差穩定于0.2 m。

圖7 PRN01星星間鏈路自主定軌算法URE誤差圖

因而，通過仿真分析，基于天文導航信息的強跟蹤自主建鏈恢復方法的有效性也得到了驗證。

4 結 論

針對星間鏈路自主定軌算法存在穩定性差，故障無法自主恢復等缺點，提出了一種天文導航信息導引的星間鏈路自主定軌算法。算法將天文導航獲得的衛星軌道信息引入衛星建鏈方法中，使衛星自主獲得高精度的星間建鏈指向。并在天文導航算法中加入了強跟蹤濾波處理方法，使衛星存在軌道信息偏差時，衛星可快速確定軌道并恢復鏈路建鏈。仿真結果表明，衛星平穩運行時，利用本文算法，星間仰角及方位角指向誤差均小于0.1°。而當衛星由于30 min軌道機動而導致鏈路中斷時，利用本文算法，可在5000 s內使衛星鏈路指向精度恢復至0.1°。本文算法極大地提高了衛星星間鏈路自主定軌的自主性及穩定運行能力。