基于序列凸規(guī)劃的運載火箭軌跡在線規(guī)劃方法

程曉明，尚 騰，徐 帆，王晉麟，姚寅偉

(北京航天自動控制研究所，北京 100854)

0 引 言

隨著世界各航天強國對外層空間開發(fā)與利用的不斷深化，運載火箭需要在處理故障與自主飛行方面具有更強的自主控制能力[1]。因此，軌跡在線規(guī)劃技術已成為運載火箭未來進入空間的一項關鍵技術，該技術賦予火箭自主規(guī)劃與故障應變能力，能夠極大地提升火箭執(zhí)行任務的靈活性與完成新型任務的能力，也可節(jié)省飛行成本[2]。

由于大氣層內(nèi)火箭軌跡規(guī)劃模型的復雜性，在面對突發(fā)任務、故障情況時，如何快速、可靠地求解出最優(yōu)飛行軌跡，是目前火箭控制中的難點之一[3]。近幾十年來，國內(nèi)外學者在軌跡規(guī)劃方法上的研究主要分為基于最優(yōu)控制原理的間接法和基于數(shù)值優(yōu)化的直接法。如文獻[4-8]基于間接法的思想，研究了氣動影響下的最優(yōu)軌跡規(guī)劃方法，通過求解包含橫截條件的兩點邊值問題的思路，對最優(yōu)軌跡進行直接求解。這種方法形式簡單，但較為依賴初始協(xié)態(tài)猜想，收斂速度較慢，導致其實用性大打折扣。

隨著計算機技術的發(fā)展及其運算能力的提升，基于數(shù)值方法的直接法得到較快的發(fā)展[9]。如文獻[10-15]利用直接多步打靶法、偽譜法等對火箭的軌跡規(guī)劃進行了大量的研究，驗證了直接法應用于火箭軌跡規(guī)劃上的有效性。這些方法的優(yōu)化結(jié)果精度較高，但由于離散變量多，計算量大，導致算法的實時性不足。另外，這些算法在理論上缺少收斂性證明。

為了進一步保證數(shù)值算法的收斂性與實時性，將軌跡規(guī)劃問題轉(zhuǎn)化為一個凸規(guī)劃問題，能利用凸規(guī)劃求解算法(如內(nèi)點法)所具有的多項式時間收斂特性，以同時滿足算法收斂性與實時性要求。近年來，文獻[16-17]利用凸優(yōu)化理論研究了火星著陸在線軌跡規(guī)劃問題，文獻[18-19]針對大氣層外入軌問題的軌跡規(guī)劃問題，研究了基于凸優(yōu)化的軌跡規(guī)劃方法。然而，對于地球大氣層內(nèi)的運載火箭軌跡規(guī)劃問題，其氣動模型的復雜性使其不能簡易的轉(zhuǎn)化為凸規(guī)劃問題而得到求解，因此，需要進一步研究大氣層內(nèi)火箭軌跡規(guī)劃問題的快速求解方法。

序列凸規(guī)劃[20]是一項求解非凸規(guī)劃問題的局部優(yōu)化方法，通過序列逼近的方式，將原非凸規(guī)劃問題轉(zhuǎn)化為序列凸規(guī)劃問題，并進行序列求解。文獻[21]通過序列線性化的方式，將序列凸優(yōu)化應用于航天器的軌跡優(yōu)化中。文獻[22-24]基于序列凸規(guī)劃的思想，研究了火箭的自主軌跡規(guī)劃方法。但在目前的這種方式中，模型的凸化均是基于對非線性模型的線性化方式，這種方式會造成任務狀態(tài)變化較大時軌跡在線規(guī)劃模型的失準，且依賴初始猜想軌跡，對任務的適應性較弱。

本文基于序列凸規(guī)劃思想，研究了一種模型補償序列凸規(guī)劃方法，該方法不需要初始猜想，其核心思想是序列地利用前一次規(guī)劃得到的最優(yōu)軌跡，補償下一次迭代時軌跡規(guī)劃問題中動力學的非線性項(軸向力加速度、法向力加速度和重力加速度)與過程約束，直到前后兩次迭代的最優(yōu)解收斂。通過在序列凸規(guī)劃問題中增加柯西約束，保證得到的序列最優(yōu)解為一組柯西序列，從而保證了該方法的收斂性。最后針對火箭上升段與著陸段的軌跡規(guī)劃問題對該算法進行仿真校驗。

1 火箭軌跡規(guī)劃問題描述

1.1 火箭運動方程

在發(fā)射點慣性坐標系下，建立火箭的運動方程為：

(1)

式中：r=[x,y,z]T表示位置，v=[vx,vx,vx]T表示速度，m為飛行器質(zhì)量，g=[gx,gx,gx]T表示重力加速度，T=[Tx,Tx,Tx]T表示飛行器推力。Isp為飛行器的比沖，g0為海平面的重力加速度大小。A和N分別為飛行器氣動力中的軸向力與法向力。

1.2 約束與性能指標

1.2.1控制約束與狀態(tài)約束

假設飛行器的比沖不隨飛行狀態(tài)改變，但推力可以通過節(jié)流閥門進行調(diào)節(jié)，根據(jù)節(jié)流閥的最小與最大節(jié)流程度，可得推力的約束范圍為：

(2)

通常，飛行器的當前狀態(tài)作為初始端點約束

s(t0)=s0∈R7

(3)

(4)

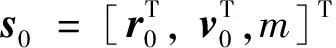
令飛行器的凈重為mdry，初始質(zhì)量m0,飛行器的燃料約束描述如下：

M={m(t)∈R+:mdry≤m(t)≤m0, ?t∈[0,tf]}

(5)

1.2.2過程約束

火箭在大氣層內(nèi)飛行時，考慮三種常見的過程約束：動壓約束、軸向過載約束和彎矩約束。

(6)

(7)

|qα|≤Qα max

(8)

式中：qmax，amax和Qα max分別為動壓約束、軸向過載約束和彎矩約束的最大允許值。α為飛行器的攻角，由飛行器體軸與速度軸的夾角構成。

1.2.3性能指標

考慮最省燃料這一性能指標：

(9)

由于飛行器的質(zhì)量是單調(diào)遞減的，因此可將最省燃料的性能指標(9)轉(zhuǎn)化為梅耶(Mayer)形式：

minJ=-m(tf)

(10)

因此，本文火箭軌跡規(guī)劃問題的主要目標便是求解最優(yōu)的推力矢量T(t)∈R3，使其滿足各約束的同時，令性能指標(式(10))最小。

2 基于序列凸規(guī)劃的軌跡規(guī)劃方法

2.1 模型補償序列凸規(guī)劃方法

模型補償序列凸規(guī)劃方法的核心是如何序列地補償大氣層內(nèi)軌跡規(guī)劃問題中的非線性項，使其逼近真實的氣動加速度模型與重力加速度模型，因此，為了在后續(xù)方法設計中對這些非線性項進行較為直觀的處理，將火箭的動力學方程重新描述為：

(11)

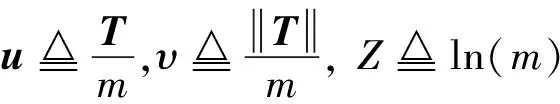
并將控制量增廣為：η=[υ,uT]T，控制約束可以重新寫為：

(12)

0≤Tmine-Z≤υ≤Tmaxe-Z

(13)

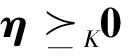
U(t)={η(t)=[υ(t),uΤ(t)]Τ∈R4:

0≤Tmine-Z[k-1](t)≤υ(t)≤Tmaxe-Z[k-1](t)

(14)

由于軸向力加速度a、法向力加速度n、重力加速度g以及過程約束的非線性，導致該問題無法得到快速求解，因此本文研究了模型序列補償?shù)姆绞剑缘姆绞綄@些非線性項進行逐步逼近，最終收斂到真實的模型，并提出了針對大氣層內(nèi)火箭軌跡規(guī)劃問題的模型補償序列凸規(guī)劃方法。

2.1.1模型序列補償方法

模型序列補償方法的實現(xiàn)策略是，在第一次迭代中，將動力學中的非線性項建模為時間的線性函數(shù)，并將非凸最優(yōu)控制問題轉(zhuǎn)化為一個凸規(guī)劃問題進行求解；然后在后續(xù)迭代中，利用前一次迭代產(chǎn)生的最優(yōu)解對這些非線性項模型進行序列補償，直到其收斂到真實模型。

為了便于描述，將動力學中的非線性項(包括重力加速度、氣動力)以一個新的變量表示：

ψ(t)=g(t)+a(t)+n(t)

(15)

在序列迭代補償方案設計中，在序列補償?shù)牡谝淮诬壽E優(yōu)化時，根據(jù)軌跡規(guī)劃任務的始末狀態(tài)，將自動給出這些非線性項的初始線性猜想，其次基于該模型形成的凸規(guī)劃問題，利用凸優(yōu)化方法進行快速軌跡求解，然后將前一次得到的結(jié)果對下一次優(yōu)化時動力學模型中的ψ(t)進行補償。表示如下：

ψ(k+1)(t,s(k))=g(k)(t,s(k))+a(k)(t,s(k))+

n(k)(t,s(k))

(16)

通過上述補償方式，可以將火箭軌跡規(guī)劃問題轉(zhuǎn)化為序列求解凸規(guī)劃問題，直到模型ψ(t)收斂。

2.1.2過程約束的序列凸化

在模型補償序列凸規(guī)劃方法中，對過程約束的凸化采用了利用前一次迭代產(chǎn)生的最優(yōu)解對后續(xù)迭代中的過程約束進行序列凸化的策略。主要包括：

1)動壓約束

通過分析動壓函數(shù)對高度和速度的海森陣可知，動壓約束(6)不是一個凸約束。

為了滿足本文所提出的算法在求解最優(yōu)控制問題時對凸模型的需求，利用前一次迭代得到的最優(yōu)解，對動壓約束進行如下近似：

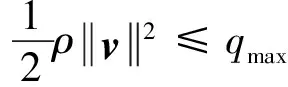
(17)

2)軸向加速度約束

根據(jù)前文所述的變量替換方法，軸向加速度約束可以基于前一次迭代得到的重力加速度，寫為：

(18)

因此，軸向加速度約束可以簡單的轉(zhuǎn)化為凸約束。

3)彎矩約束

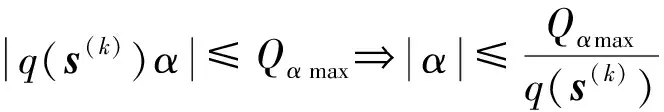
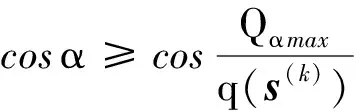
(19)

(20)

此時，通過利用前一次迭代的最優(yōu)軌跡結(jié)果將過程約束轉(zhuǎn)化為凸約束

2.1.3凸模型下的大氣層內(nèi)火箭軌跡規(guī)劃問題

通過對控制量約束、動力學模型與過程約束進行序列凸化后，非凸的大氣層內(nèi)火箭軌跡規(guī)劃問題可以建模為凸最優(yōu)控制問題(21)。

η∈U(t),s∈Χ(t)，[s,η]∈P(t)，s(t0)=s0

U(t)={η(t)=[(υ(t),uΤ(t)]Τ∈R4:

0≤Tmine-Z[k](t)≤υ(t)≤Tmaxe-Z[k](t)

Χ(t)={s(t)∈R7:smin≤s(k)≤smax,

Z(t)≥ln(mdry)}

(21)

2.2 基于模型補償序列凸規(guī)劃對火箭軌跡規(guī)劃算法描述

采用等間隔方法，對凸最優(yōu)控制問題(21)進行離散。通過將時間區(qū)間進行離散、并將最優(yōu)控制問題中的各種約束限制在每個離散點上的方式，將無窮維的連續(xù)線性凸最優(yōu)控制問題轉(zhuǎn)化為有限維的參數(shù)優(yōu)化問題。由于該最優(yōu)控制問題中的約束均為線性約束或二階錐約束，因此離散后將得到一個二階錐規(guī)劃問題，從而可以使用有效的凸優(yōu)化求解方法對其進行實時求解。

對于給定的時間區(qū)間[0,tf]，取等間隔時間區(qū)間為Δt，那么每個離散點對應的時刻為：

tk=nΔt,n=0,…,N

(22)

式中：N=tf/Δt為離散點的個數(shù)。控制變量采用零階保持，即在時間區(qū)間t∈[tn,tn+1)內(nèi)，控制量為ηn=η(tn)。

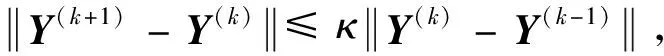
基于上述狀態(tài)變量與控制變量的離散和已知的時間區(qū)間，式(21)所描述的連續(xù)凸最優(yōu)控制問題可以轉(zhuǎn)化為一個離散凸最優(yōu)控制問題：

(23)

式中：上標(k+1)代表第(k+1)次迭代，即當前迭代，下標n代表第n個離散點。由式(23)確定的最優(yōu)控制問題中的動力學方程可以看作是一個線性時不變方程。僅有ψ(k+1)會隨著時間改變，但其各離散點的值均已知。性能指標函數(shù)為關于終端狀態(tài)的凸函數(shù)，可以將其離散為關于最后一個離散點處狀態(tài)的函數(shù)，該函數(shù)的凸性不變。因此，可以認為式(23)這一離散凸最優(yōu)控制問題可以逼近原連續(xù)凸最優(yōu)控制問題(21)。

式(23)中的離散狀態(tài)空間矩陣為：

(24)

其中，η=[uΤ,υ]Τ;矩陣Ac,Bc和Cc分別為

(25)

(26)

(27)

在完成凸規(guī)劃問題的離散建模后，該問題可利用原始-對偶內(nèi)點法對其進行快速求解。因此，在進行火箭軌跡規(guī)劃算法設計時，基于模型序列補償方法，對離散凸規(guī)劃問題進行重復求解，當max(s(k+1)-s(k))

定理1.當給定的初始離散設計變量在可行域內(nèi)時，即Y(0)∈M?RNY，模型補償序列凸規(guī)劃算法在有限次迭代后能夠收斂到定點最優(yōu)解Y*∈M。

證.由于本文提出的模型補償序列凸規(guī)劃算法增加了柯西約束：

(28)

在迭代解的更新中，序列凸規(guī)劃算法自映射迭代算子：φ:M?RNY→M?RNY表示離散可行設計變量Y(k)的更新，即輸入由前一次迭代k得到的全體設計變量Y(k)，該算子能夠在迭代k+1中得到狀態(tài)量Y(k+1)：

Y(k+1)=φ(Y(k))

(29)

當增加了式(28)描述的柯西約束后，可知離散凸優(yōu)化模型補償?shù)蛄衁(k)=φ(Y(k-1))=φ(k)(Y(0)),k=1,2,…,M為一個柯西序列。當式(29)給出的柯西序列有界時，該柯西序列可收斂到定點最優(yōu)解Y*=φ(Y*)∈M。

定理2.假設由式(23)表示的離散凸最優(yōu)控制問題通過模型補償序列凸規(guī)劃算法，收斂到一個離散最優(yōu)解Y*，那么由這個解逼近得到的連續(xù)解([r*,v*,m*],T*)是原非凸最優(yōu)控制問題的一個局部最優(yōu)解。

證.首先假設由式(23)表示的離散凸最優(yōu)控制問題，在模型補償序列凸規(guī)劃算法下，收斂到一個離散的最優(yōu)解Y*=(s*,η*)。根據(jù)本文對連續(xù)最優(yōu)控制問題的離散化描述，離散方法能夠逼近連續(xù)凸最優(yōu)控制問題(21)，因此連續(xù)凸最優(yōu)控制問題(21)的最優(yōu)解(s*,η*)可以由Y*逼近得到，并在此假設(s*,η*)與Y*等價。

對于由式(23)描述的最優(yōu)控制問題，矩陣Ac,Bc和Cc均為時不變矩陣，該問題的可控性克萊姆矩陣為：

(30)

式中：Φ(t,τ)為狀態(tài)轉(zhuǎn)移矩陣,Φ(t,τ)=eAc(t-τ)。

由于狀態(tài)轉(zhuǎn)移矩陣Φ(t,τ)在任意時間區(qū)間處均為滿秩，即rank(eAc(t-τ))=7，且rank(Bc)=4，可知，null(eAc(t-τ)Bc)=0，因此可知可控性克萊姆矩陣是W(t)非奇異的，最優(yōu)控制問題(23)中由[Ac,Bc]確定的連續(xù)線性動力學是可控的。

在可控性基礎上，根據(jù)文獻[16]可知，變量替換后控制量約束的松弛凸化是無損的，因此可知在每次迭代Ψ(k+1)都已知的情況下，式(21)表示的連續(xù)凸最優(yōu)控制問題的最優(yōu)解(s*,η*)，也是控制量約束“松弛”處理前的線性非凸最優(yōu)控制問題的最優(yōu)解(s*,u*)。

由離散最優(yōu)解Y*是一個定點最優(yōu)解，可知(s*,u*)也為定點最優(yōu)解。這意味著動力學非線性項Ψ(k+1)通過序列凸化，最后能夠收斂，因此(s*,u*)也是原始非凸最優(yōu)控制問題的局部最優(yōu)解。此時，通過變量反替換可知，與(s*,u*)對應的([r*,v*,m*],T*)是原非凸最優(yōu)控制問題的一個局部最優(yōu)解。

總結(jié)上述基于模型序列補償凸規(guī)劃的火箭軌跡規(guī)劃算法，下面將算法流程描述如下。

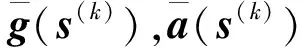
第二步：基于線性化后的重力/氣動加速度猜想值與過程約束凸化方法，利用無損凸化與變量替換技術，將軌跡規(guī)劃問題轉(zhuǎn)化為凸規(guī)劃問題，并進行求解后儲存為軌跡k，軌跡狀態(tài)為s(k)。

第三步：計算軌跡k上狀態(tài)s(k)對應的重力/氣動力加速度值g(s(k)),a(s(k))和n(s(k))，將其補償?shù)阶顑?yōu)控制問題(23)的建模中。

第四步：求解式(23)，得到軌跡k+1。

第五步：如果軌跡k+1與軌跡k中對應狀態(tài)的差小于允許的閾值，則停止程序；否則，令k=k+1，返回第三步。

3 數(shù)值仿真與分析

為了檢驗本文所提出模型補償序列凸規(guī)劃方法的有效性，以火箭大氣層內(nèi)軌跡在線規(guī)劃任務為背景，對該方法進行仿真校驗。數(shù)值仿真平臺為PC機，性能為Inter Core i7-6700 3.4 GHz，仿真軟件采用了MATLAB2014a，其中的凸優(yōu)化求解軟件采用了CVX工具箱[25]。

本節(jié)主要通過大氣層內(nèi)軌跡規(guī)劃的兩個方面進行數(shù)值仿真實驗設計：1)火箭上升段軌跡自主規(guī)劃仿真；2)火箭著陸段軌跡自主規(guī)劃仿真。

3.1 火箭上升段軌跡自主規(guī)劃仿真與分析

火箭上升段軌跡自主規(guī)劃仿真采用的火箭模型以及基本任務參數(shù)設置如表1所示。

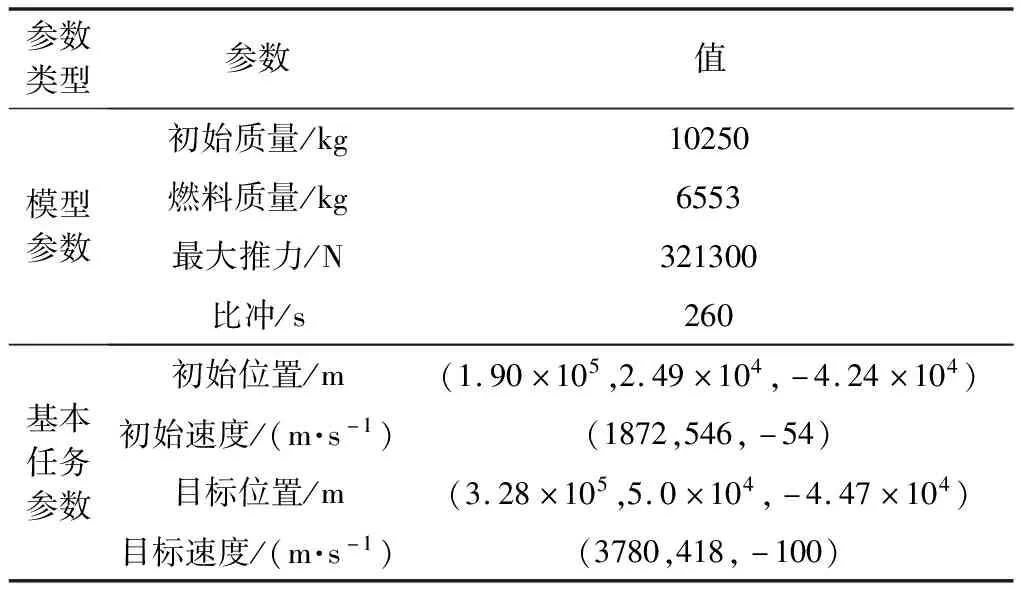
表1 上升段火箭模型與任務參數(shù)設置

圖1中，標記“·”的曲線代表最后一次迭代得到的最優(yōu)推力大小曲線。圖2中，標記“·”的曲線代表最后一次迭代得到的最優(yōu)俯仰角和偏航角指令曲線。

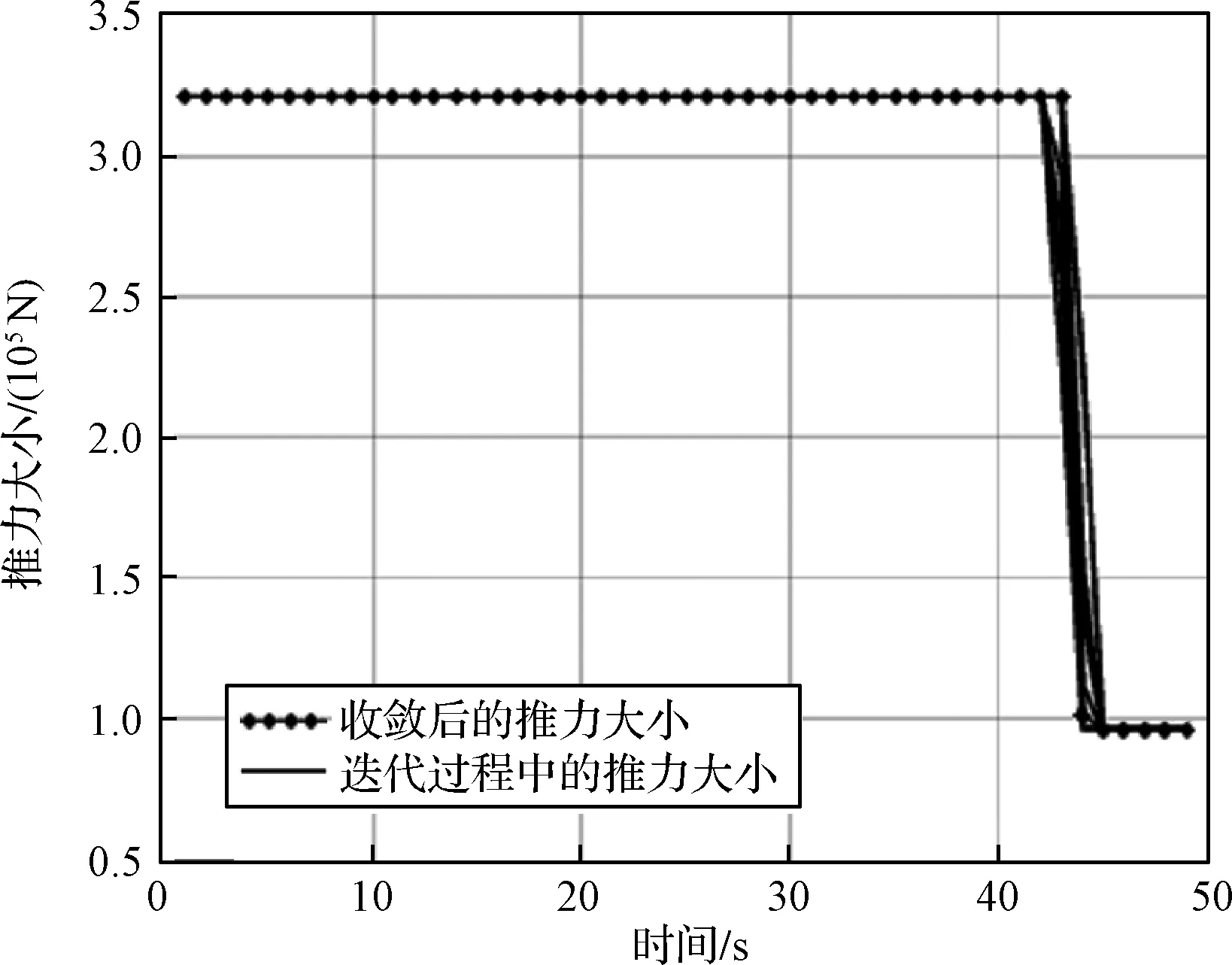
圖1 上升段推力大小變化曲線

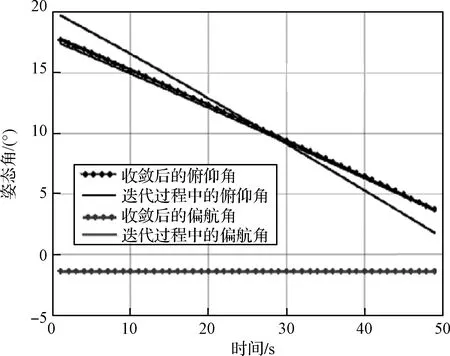
圖2 上升段姿態(tài)角變化曲線

經(jīng)過仿真校驗，基于該推力曲線，模型補償序列凸規(guī)劃方法得到的最優(yōu)軌跡能夠精確滿足表1中給定的火箭上升段終端狀態(tài)約束與控制量約束。

圖3中，標記“·”的曲線代表最后一次迭代得到的最優(yōu)解對應的氣動加速度變化曲線。從圖3可以看出，氣動加速度曲線呈現(xiàn)遞減的趨勢，這主要是隨著飛行高度的增高，大氣密度快速減小導致的。從氣動加速度的迭代過程圖可以看出，模型補償序列凸優(yōu)化方法通過對氣動力的不斷補償進行序列軌跡規(guī)劃，對氣動力補償?shù)氖諗恳馕吨撔蛄蟹椒ǖ氖諗俊?/p>

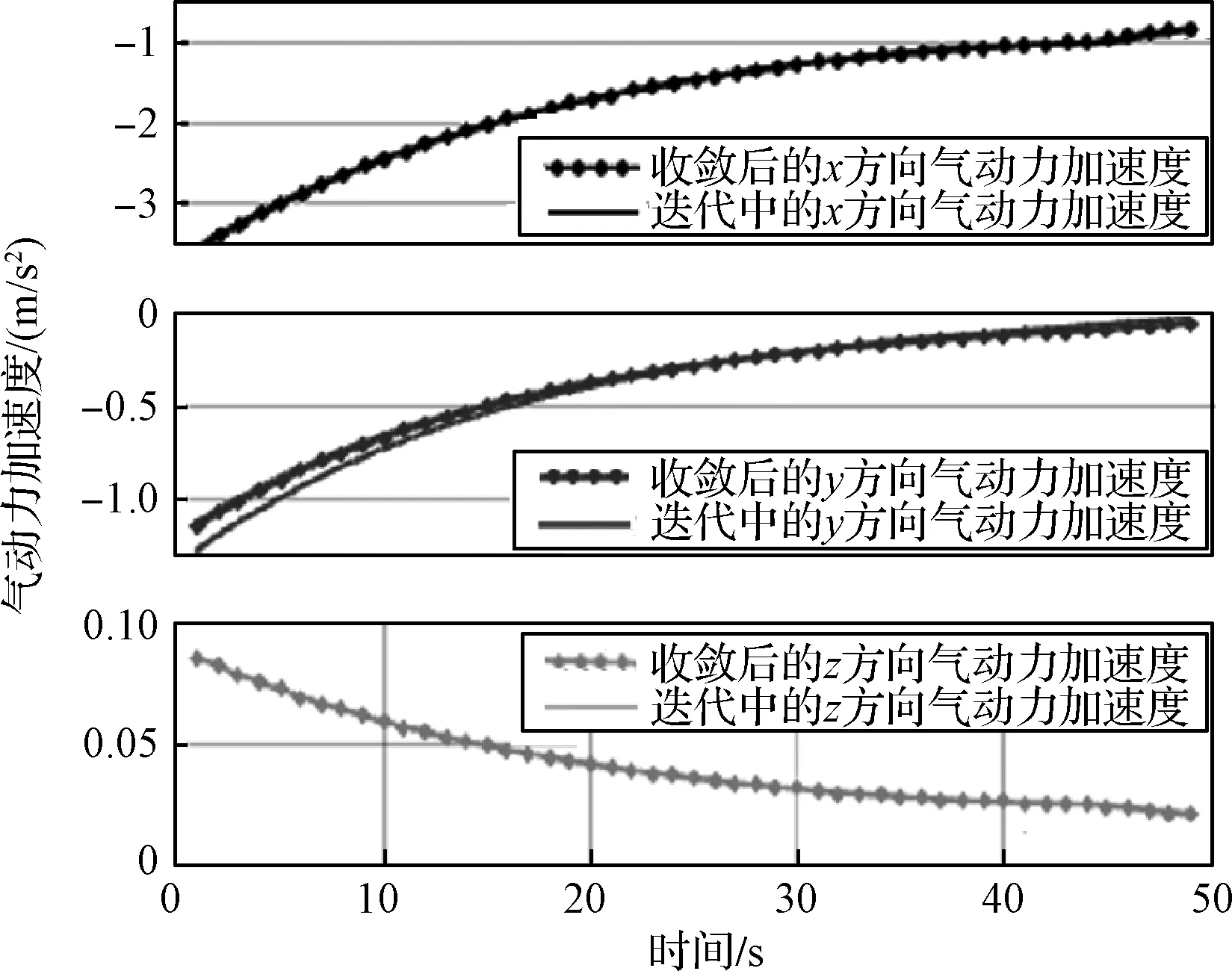
圖3 上升段氣動力加速度在發(fā)慣系三個方向分量的變化曲線

在軌跡規(guī)劃收斂時間方面，該任務仿真時通過7次迭代后收斂，共耗時1.5 s，平均每次迭代耗時0.21 s；本次數(shù)值仿真對應50個離散點(以1 s為等時間間距進行離散)，當實際任務需要進一步減少軌跡生成時間時，可以在軌跡精度允許范圍內(nèi)，增大離散點間隔，從而通過減少離散點個數(shù)的方式加快軌跡生成速度。

3.2 火箭垂直著陸段軌跡自主規(guī)劃仿真與分析

對于火箭垂直著陸任務，需要在火箭著陸時刻保持火箭速度為0，且箭體豎直向上。另外，通常要求火箭在著陸階段燃料消耗最省，以節(jié)省火箭的發(fā)射成本、提高火箭的有效載荷重量。

仿真采用的火箭模型以及基本任務參數(shù)設置如表2所示。

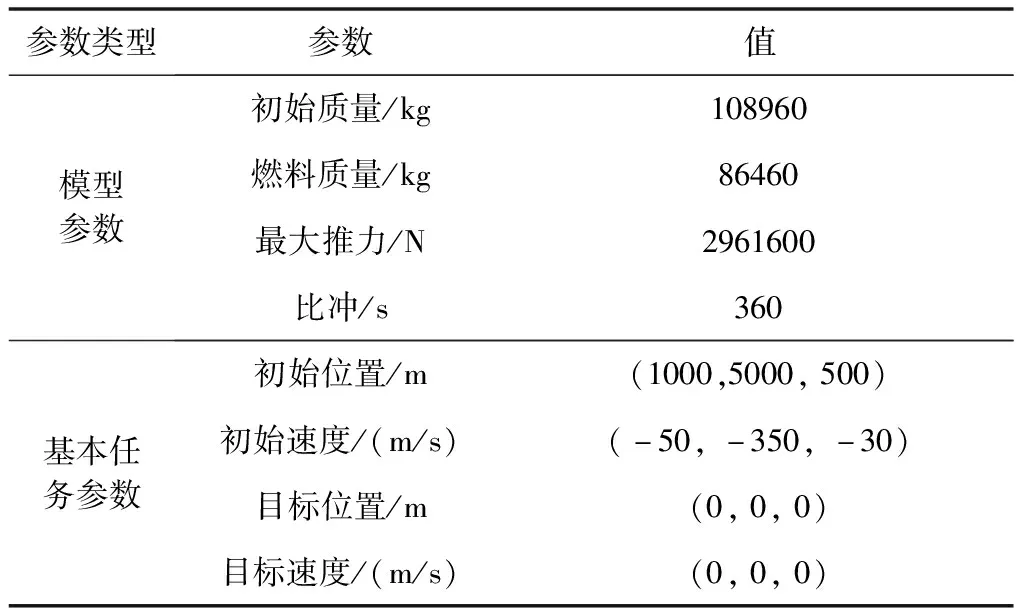
表2 著陸段火箭模型與基本任務參數(shù)設置

圖4和圖5中，標記“·”的曲線代表最后一次迭代得到的最優(yōu)飛行軌跡和最優(yōu)速度在發(fā)慣系三個方向上的分量，沒有標記“·”的曲線則代表迭代過程中得到的飛行軌跡和速度曲線。

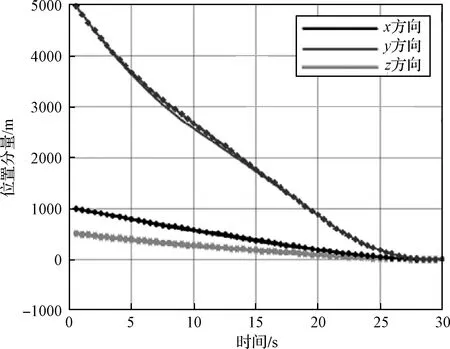
圖4 垂直著陸段位置在發(fā)慣系三個方向分量的變化曲線

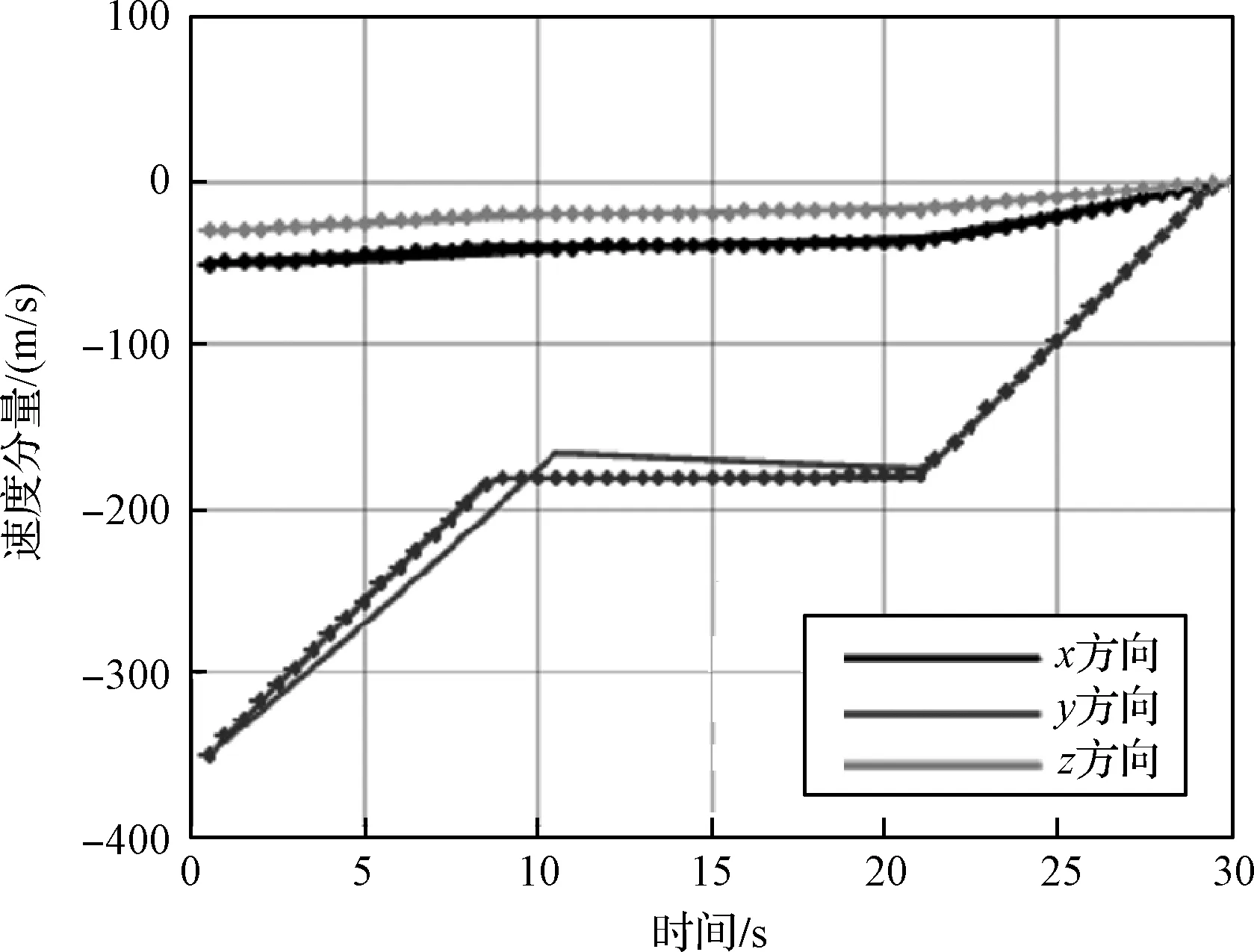
圖5 垂直著陸段速度在發(fā)慣系三個方向分量的變化曲線

每幅圖有多條曲線，代表序列迭代過程中每次迭代產(chǎn)生的最優(yōu)解曲線。雖然每次迭代產(chǎn)生的解均能滿足著陸約束，但中間迭代采用的氣動模型還處于不斷補償修正中，并不能代表真實的模型，只有最后一次模型補償收斂后得到的解，才能算是具有真實意義的最優(yōu)解。

圖6和圖7中，標記“·”的曲線分別代表最后一次迭代得到的最優(yōu)推力大小曲線和最優(yōu)俯仰角、偏航角指令曲線。仿真結(jié)果表明，基于該推力大小和姿態(tài)角形成的推力矢量，模型補償序列凸規(guī)劃方法得到的最優(yōu)軌跡能夠精確滿足火箭垂直著陸所需要的終端狀態(tài)約束條件。

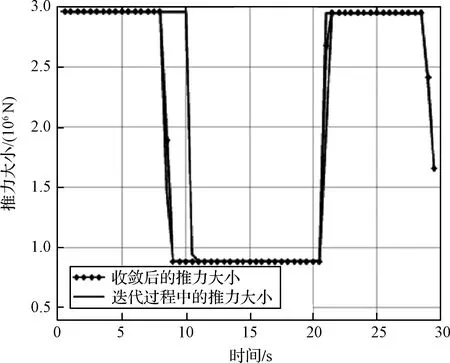
圖6 垂直著陸段推力大小變化曲線

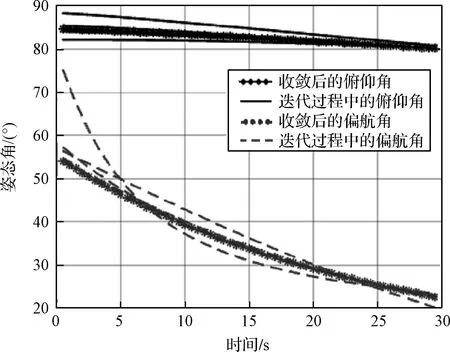
圖7 垂直著陸段姿態(tài)角變化曲線

圖8中，標記“·”的曲線代表最后一次迭代得到的最優(yōu)解對應的氣動加速度變化曲線。從圖8可以看出，火箭在著陸過程中，氣動加速度也會隨著速度的降低而減小，最后時刻減小為0。從氣動加速度的迭代過程圖可以看出，模型補償序列凸規(guī)劃方法對氣動加速度進行了序列的補償并最終收斂。

圖8 垂直著陸氣動力加速度在發(fā)慣系三個方向分量迭代更新圖

最后，在軌跡規(guī)劃收斂時間方面，該任務仿真時通過8次迭代后收斂，共耗時2 s，平均每次迭代耗時0.25 s；每次迭代所需時間與離散點個數(shù)、約束數(shù)量相關，本次數(shù)值仿真對應60個離散點(以0.5 s為等時間間距進行離散)，當實際任務需要進一步減少軌跡生成時間時，可以在軌跡精度允許范圍內(nèi)，通過增大離散點間隔，減少離散點個數(shù)的方式進行處理。

綜合以上仿真結(jié)果可知，本文提出的模型補償序列凸規(guī)劃方法可以通過序列補償?shù)姆绞教幚泶髿鈱觾?nèi)非線性氣動力對軌跡規(guī)劃帶來的不利影響。在利用該方法對軌跡規(guī)劃問題序列求解時，火箭的氣動力通過不斷的補償最終收斂到準確的氣動模型，同時也完成了方法的收斂迭代過程，這一快速收斂性將有利于滿足火箭軌跡自主規(guī)劃任務對軌跡優(yōu)化實時性的需求。

4 結(jié) 論

針對大氣層內(nèi)的火箭軌跡自主規(guī)劃問題，本文研究了一種模型補償序列凸規(guī)劃方法。該方法對火箭軌跡規(guī)劃問題的非線性項(軸向力加速度、法向力加速度和重力加速度)和過程約束進行了序列補償方案設計，結(jié)合無損凸化和變量替換技術，將火箭軌跡規(guī)劃問題轉(zhuǎn)化為一個序列凸規(guī)劃問題。通過在序列凸規(guī)劃問題中增加柯西約束，保證得到的序列最優(yōu)解為一組柯西序列，從而進一步保證了該方法對應求解算法的收斂性。從理論分析可知，模型補償序列凸規(guī)劃方法不需要初始猜想軌跡，具有設計簡單，自主性強的特點。最后，分別通過對大氣層內(nèi)上升段與垂直著陸段的軌跡自主規(guī)劃任務的仿真，對本文提出的模型補償序列凸規(guī)劃方法進行了校驗，得到結(jié)論如下：

1)該方法能夠較好地處理大氣層內(nèi)氣動力影響下的火箭軌跡規(guī)劃問題。

2)該方法具有較好的收斂性，能夠滿足火箭軌跡自主規(guī)劃任務對軌跡規(guī)劃問題求解的收斂性要求與實時性要求。

3)該方法對火箭的著陸段與大氣層內(nèi)上升段的軌跡規(guī)劃任務都有較好的適應性，對在線軌跡規(guī)劃在工程上的應用提供了理論基礎。