新型自減振行星傳動系統動態特性分析

史小丁，孫冬野，周 瑾，尤 勇，闞英哲

(重慶大學 機械傳動國家重點實驗室，重慶 400044)

對于發動機驅動的傳動系統的研究已經較為成熟，發動機轉矩波動劇烈對系統影響較大，一般采用扭轉減振裝置或雙質量飛輪，通過調整系統動力學參數來改善系統動態特性[5-7]。文獻[6]分析了雙質量飛輪參數對傳動系統扭振控制的影響，并在一定約束條件下進行雙質量飛輪多級扭轉剛度的匹配設計。對于電機驅動的傳動系統，文獻[8-9]建立了不同的電機模型，并分析了不同情況下電機、齒輪系統耦合的動態特性，包括狀態監測、故障診斷等。文獻[10-11]通過對電機的控制實現了傳動系統的主動降振，減小系統沖擊載荷作用下的動載荷。

1 電機-TVD-PG系統動力學模型

TVD-PG傳動系統采用扭轉減振裝置取代了傳統的行星齒輪中某一構件與箱體固連的方式，另外兩個中心構件分別作為輸入和輸出端，可組成3種不同的結構形式。以扭轉減振裝置耦合內齒圈為例，扭轉減振裝置主動端與內齒圈相連，從動端與箱體剛性固連。采用集中參數法建立了可適用于變速工況下的TVD-PG傳動系統動力學模型，其中各齒輪構件簡化為集中質量或慣量，傳動軸簡化為集中剛度和阻尼連接，忽略齒輪系統的誤差激勵、輪齒間摩擦力、齒側間隙，且單齒嚙合剛度恒定。

由于機電傳動系統經常受到來自外界和內部不斷變化的激勵作用，因此系統瞬態響應必須被考慮。與上述提到的行星齒輪動力學模型所不同，選用各構件角位移為系統廣義坐標，太陽輪和內齒圈的角位移在靜坐標系中獲得，可以與電機直接相連。所建立的適用于變速情況下的TVD-PG系統動力學模型如圖1所示。其中建立了3種坐標系：OXY為固定坐標系；Oxy為與行星架固連并隨行星架旋轉的轉動坐標系，x軸通過第一個行星輪中心；Onxnyn(n=1, 2, …,N，N代表行星輪個數)為與行星架固聯并隨行星架旋轉的轉動坐標系，On為行星輪中心，兩坐標軸分別與Oxy坐標系的兩坐標軸平行。下標c，r，s，n分別代表行星架、內齒圈、太陽輪和第n個行星輪。θi(i=c, s, r)表示構件在OXY坐標系下的角位移，θn表示行星輪在Onxnyn坐標系下的角位移；Jj(j=c, s, r,n)為構件轉動慣量；rk(k=s, r,n)為構件基圓半徑，rc為行星架有效半徑；ksn，csn，krn，crn分別為太陽輪與第n個行星輪、第n個行星輪與內齒圈間的嚙合剛度和嚙合阻尼；kr，cr分別為扭轉減振裝置扭轉剛度和阻尼；Ts，Tc分別為作用在太陽輪和行星架端的轉矩。利用牛頓定律獲得TVD-PG傳動系統數學模型，如式(1)所示。

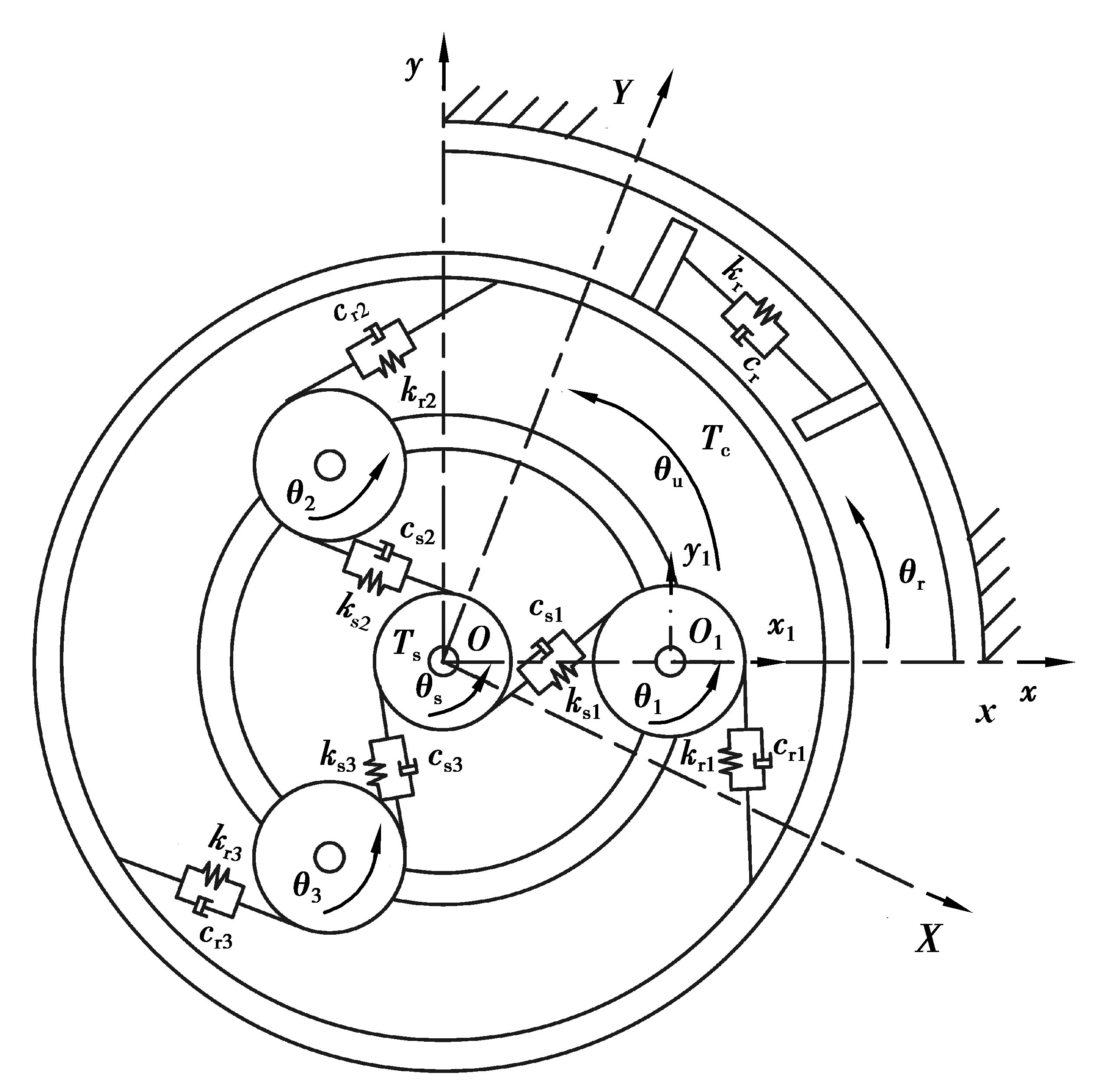
圖1 TVD-PG系統動力學模型Fig.1 Dynamic model of the TVD-PG

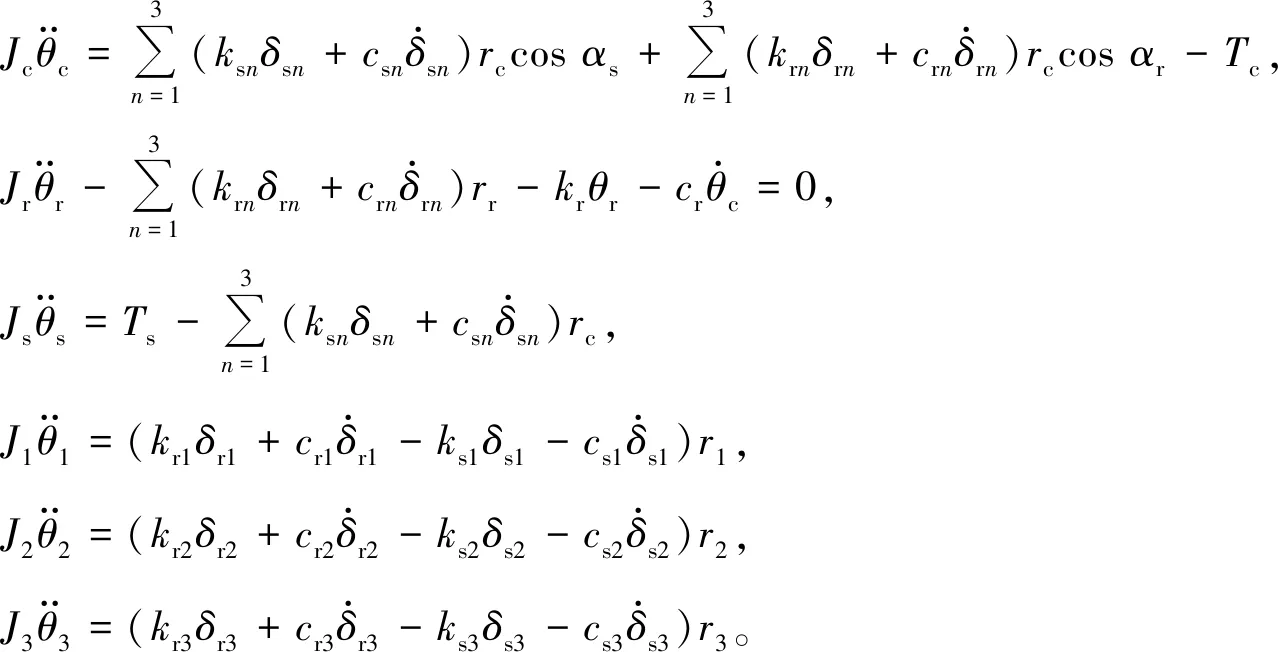
(1)

式中：δsn為太陽輪相對于第n個行星輪沿外嚙合線方向的相對變形量；δsn為內齒圈相對于第n個行星輪沿內嚙合線方向的相對變形量，表示為

(2)

建立的電機-TVD-PG傳動系統模型中選用鼠籠式異步電機，將轉子的角位移和角速度作為電機與TVD-PG傳動系統間耦合的公共變量，實時計算的電機輸出軸上的轉矩作為電機的負載，進而形成電機-TVD-PG耦合仿真模型，如圖2所示。得到電機轉子和負載端動力學方程如式(3)所示，作用在太陽輪和行星架上的轉矩由式(4)給出。

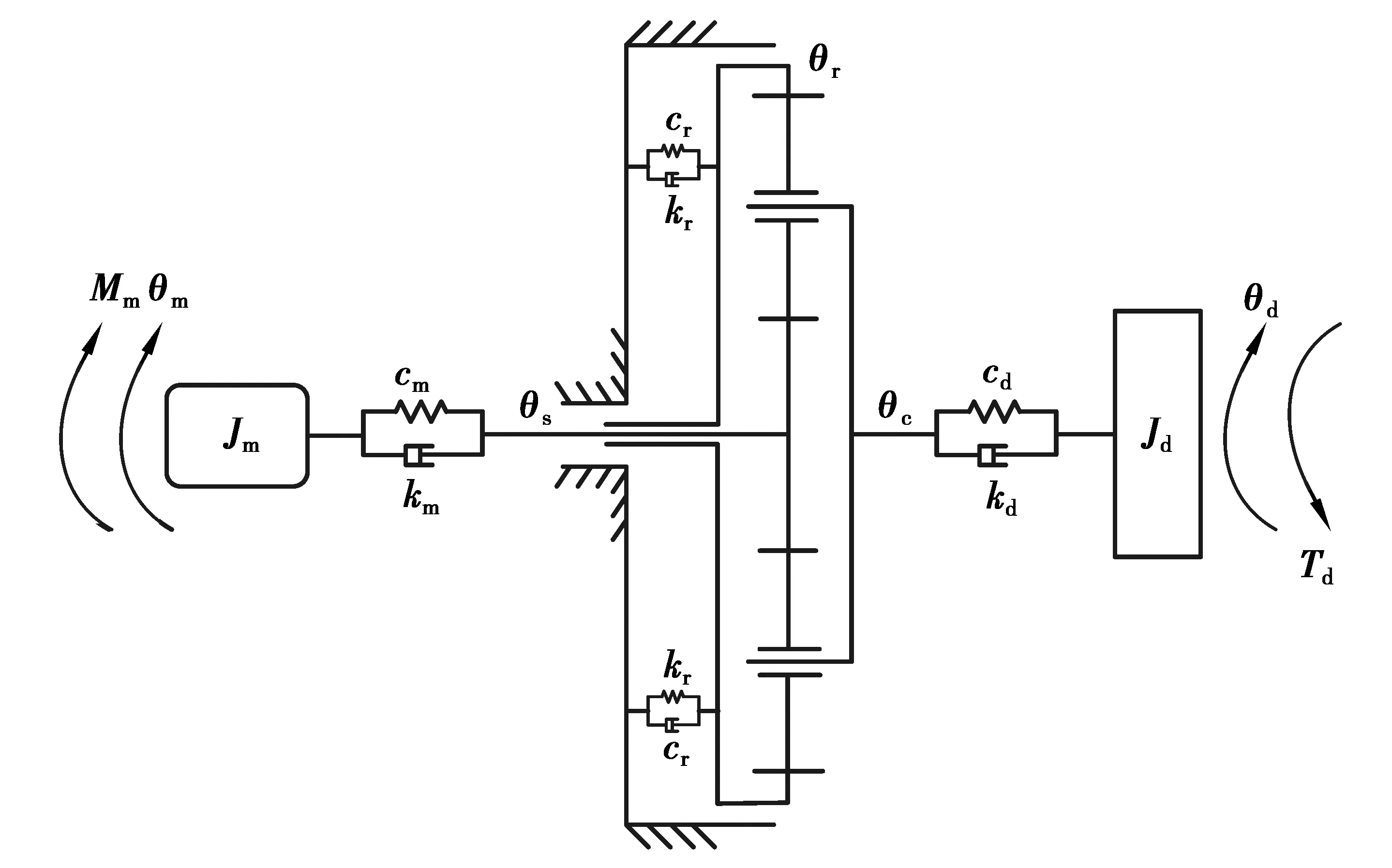
圖2 電機-TVD-PG系統模型Fig.2 Model of the motor-TVD-PG system

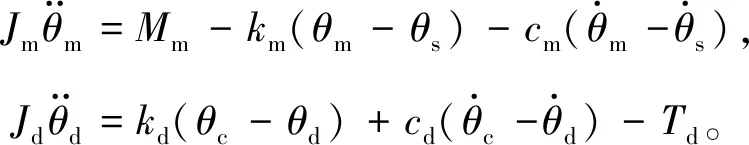
(3)

(4)

電機-TVD-PG傳動系統動力學方程可表示為矩陣方程的形式，即

(5)

式中：q為廣義坐標陣列

(6)

M為質量矩陣

(7)

T為外力矩陣

T=[Tm0 0 0 0 0 0Td]T；

(8)

Km，Kt，Kb，Cm，Ct，Cb分別為嚙合剛度矩陣、扭轉剛度矩陣、支撐剛度矩陣、嚙合阻尼矩陣、支承阻尼矩陣和支撐阻尼矩陣。其中(Km+Kt+Kb)整體可表示為系統剛度矩陣K，其形式如式(9)所示，系統阻尼矩陣(Cm+Ct+Cb)與剛度矩陣形式類似，這里不再列出。仿真所用到的TVD-PG傳動系統主要參數見表1。

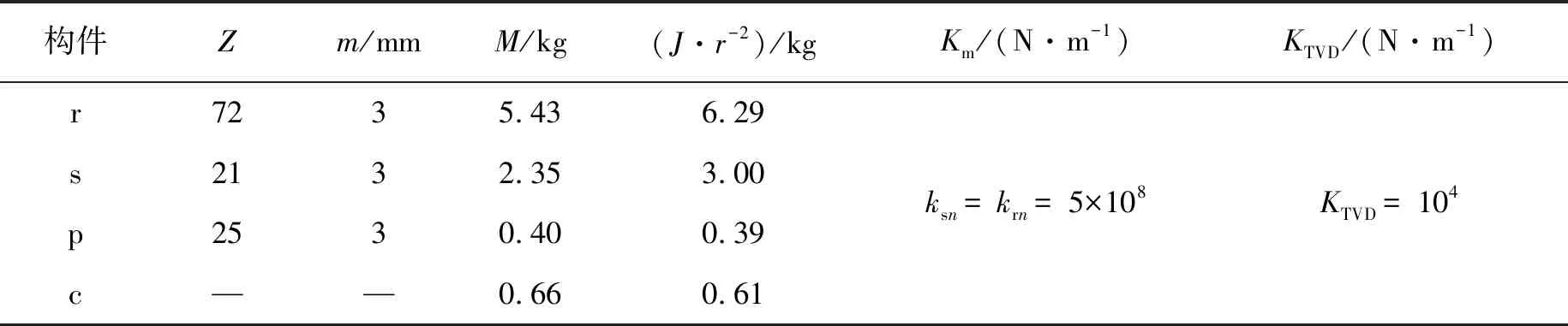
表1 TVD-PG傳動系統參數Table 1 TVD-PG system parameters

(9)

說明：p代表行星輪，Z為齒數，m為模數，M為質量，Km為等效嚙合剛度，KTVD為扭轉減振裝置剛度。

2 行星齒輪系統時變嚙合剛度模型

由于TVD-PG傳動系統需要適用于變速工況，齒輪系統嚙合頻率將隨轉速不斷變化，且系統轉速作為未知量，需要實時計算，因此系統的內部激勵參數將不能再表示為關于時間的函數，參考文獻[9,20]的方法，將行星齒輪時變嚙合剛度表示為關于太陽輪實際角位移的函數，并建立了時變嚙合剛度函數模型。時變嚙合剛度可表示為嚙合剛度均值和變動量之和的形式：

(10)

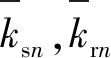
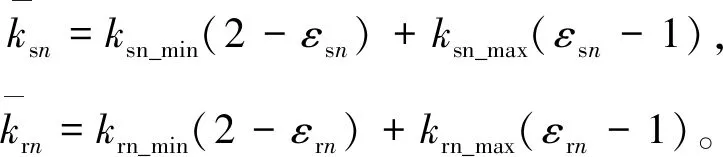
(11)

(12)

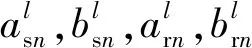
(13)

式(11)～(13)中，ksn_max，krn_max，ksn_min，krn_min分別為內、外嚙合剛度的最大和最小值；εsn，εrn分別為內、外嚙合重合度；l為諧波次數；Zs，Zr分別為太陽輪和內齒圈齒數；θs，θc分別為太陽輪和行星架的實際角位移；ψn為第n個行星輪中心與坐標原點O的連線同坐標系Oxy中x軸的夾角；γsr為內外嚙合相位差。

建立了關于太陽輪實際角位移的時變剛度模型，得到系統轉速變化時行星齒輪系統中太陽輪和第1個行星輪間的時變嚙合剛度ks1如圖3(a)所示，可以看出嚙合頻率隨轉速變化而不斷改變。為了顯示該嚙合剛度模型的嚙合頻率，圖3(b)給出了恒速時嚙合剛度的頻域信號，其中fm，2fm，3fm，4fm分別表示行星齒輪前4階嚙合頻率。

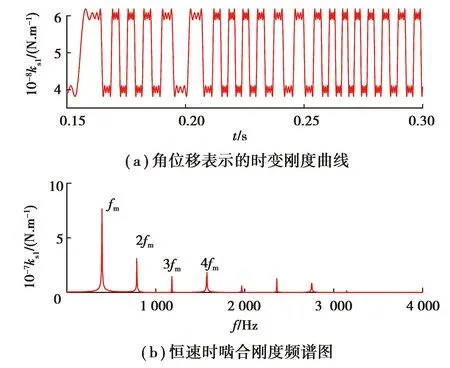
圖3 時變嚙合剛度Fig.3 Time-varying meshing stiffness

3 電機-TVD-PG系統動態特性

在建立的電機-TVD-PG傳動系統機電耦合模型基礎上，探究了考慮齒輪系統內部時變嚙合剛度激勵作用時，在啟動和穩定過程中系統的動力學特性，并與傳統的行星齒輪傳動系統仿真結果進行對比，以表明其所具備的優勢。

3.1 啟動過程中電機-TVD-PG系統動態響應

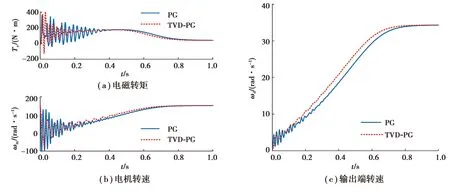
圖4 系統響應曲線Fig.4 Response curves of systems

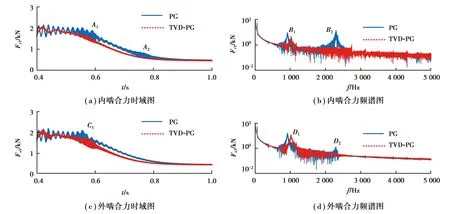
圖5 行星齒輪內、外嚙合力曲線Fig.5 Internal and external meshing force curves

3.2 穩定時電機-TVD-PG系統動態響應

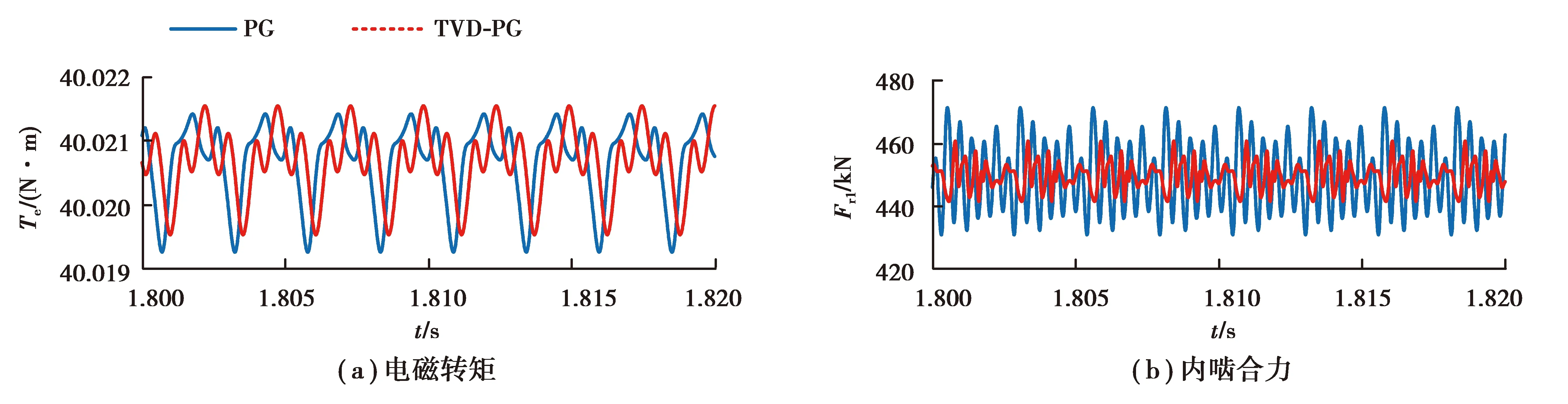
圖6 穩態響應曲線Fig.6 Steady state response curves

振動、噪聲是齒輪系統重要的動力學特性，由于電機和齒輪系統的耦合作用，齒輪系統的振動必將對電機部分造成一定的影響，這也是產生圖6(a)現象的原因。為了分析這種激勵特性，圖7給出了電機-TVD-PG系統穩定時電機電磁轉矩Te和電機轉速ωm的頻譜圖，兩圖中均可以清晰觀察到行星齒輪時變嚙合剛度的激勵頻率成分fm，2fm，3fm，4fm，…，且為各頻譜圖中的主要頻率成分。因此機電系統間的耦合作用在實際情況中應予以充分考慮，同時可利用這一特性，通過電機中便于檢測的電信號來識別齒輪系統的工作狀態或進行故障檢測等。

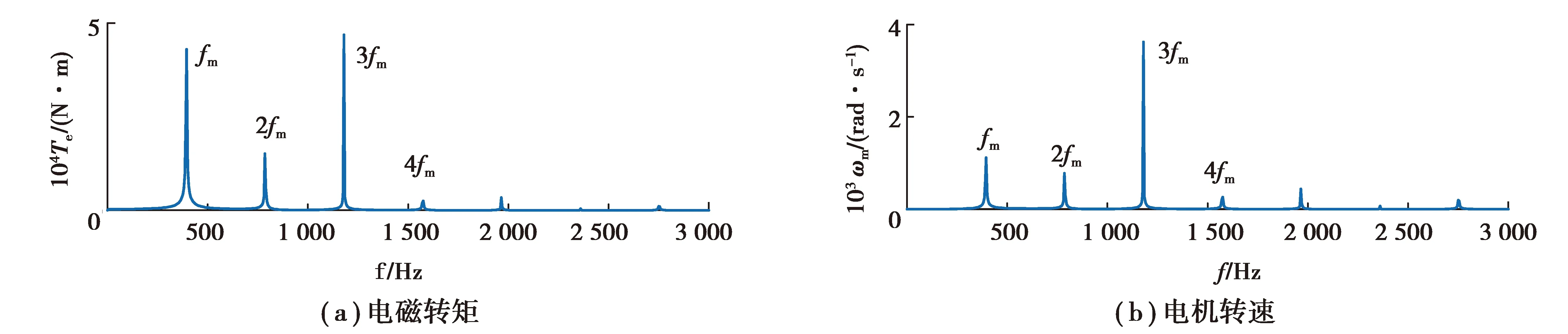
圖7 電機響應頻譜圖Fig.7 Motor response spectrums

4 結 論

1)在啟動過程中，TVD-PG傳動系統大幅降低電機電磁轉矩的波動，使電機和輸出端轉速較平穩地增長，電機和齒輪系統可以更快達到穩定狀態。同時大幅度減小啟動過程中行星齒輪內、外嚙合力的波動幅值，并減少系統升速過程中的共振區域，有助于降低齒輪系統動載荷。

2)在達到穩定時，系統依舊受到內部激勵的作用，進而表現出一種動態穩定的狀態。由于機電耦合作用的影響，在電機響應曲線中可以清晰觀察到行星齒輪時變剛度激勵的頻率成分。TVD-PG對電機電磁轉矩的影響不明顯，但可以有效降低機電傳動系統穩定時齒輪系統嚙合力的波動幅值，改善齒輪嚙合狀況。