含區間鉸間隙柔性機械臂控制精度分析

劉志元，孫東陽

(重慶大學 航空航天學院，重慶 400044)

隨著空間技術的快速發展，大尺寸、輕量化的空間機械臂已經被廣泛地用于空間站的組裝、修理和檢測，航天員艙外活動，空間飛行器捕獲等，其可靠性對于整個空間任務至關重要。空間機械臂動力學分析涉及運動過程中大變形和間隙碰撞問題，且結構參數存在不確定性，因此，要建立精確的空間機械臂動力學模型就需要考慮各種因素。

Flores等[1]對多種間隙模型進行了研究，通過對含間隙機構進行動力學分析發現間隙嚴重影響機構動力學特性。Zhao等[2]對含間隙空間機器人進行了動力學特性研究，研究發現間隙尺寸會顯著影響機器人動力學特性。Erkaya[3]建立了含間隙焊接機械臂的動力學模型。Varedi-Koulaei等[4]采用粒子群算法對含間隙的3-RRR并聯機械手進行了優化設計，以減小間隙碰撞對該機械手動力學特性的影響。Megahed等[5]對含多間隙機構進行了研究，結果表明間隙位置，運行速度和間隙大小都會顯著影響機構動力學特性。谷勇霞等[6]研究了間隙尺寸和間隙關節數量對漂浮空間機械臂動力學特性的影響。考慮到構件柔性，Khemili等[7]對含間隙平面柔性機構進行了動力學分析，結果顯示構件柔性能夠有效控制碰撞力峰值。任武等[8]建立了考慮間隙的多柔體臂架的剛柔混合模型。Ben Abdallah等[9]對含多間隙的柔性機構進行了研究。考慮到機械臂在運動過程中存在大變形，Tian等[10]基于絕對節點坐標法[11]對含PD控制器的雙連桿柔性機械臂進行了控制精度分析。然而，在建模過程中忽略了間隙對機械臂控制精度的影響。

上述研究都認為機械臂為理想情況，然而由于材料不均勻、加工誤差、摩擦、磨損等，真實的機械臂中普遍存在不確定性。Li等[12]研究了存在隨機不確定性的含間隙機械臂動力學特性和運動精度問題，建模過程中忽略了機械臂存在的變形。Wang等[13]采用Chebyshev多項式方法對存在區間不確定性參數的剛柔耦合空間機械臂進行了動力學分析，建模過程中忽略了間隙碰撞。筆者將系統考慮大變形、間隙碰撞和不確定性對機械臂動力學特性和控制精度的影響，研究含區間鉸間隙的柔性機械臂動力學建模和控制精度分析方法。

1 旋轉鉸間隙建模

1.1 旋轉鉸間隙數學模型

如圖1所示，體i,j之間存在平面間隙轉動副，軸承是體i的部件，軸是體j的部件。整體坐標系為xy。點Pi和Pj分別為軸承和軸的中心，對應的位置矢量分別為ri和rj。軸與軸承的中心距矢量eij可表示為

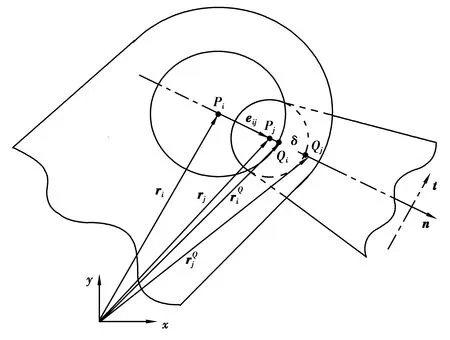
圖1 旋轉鉸間隙模型Fig.1 Revolute joint with clearance

eij=rj-ri。

(1)

軸與軸承中心距為

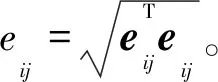
(2)

垂直軸承與軸接觸表面的單位法向量為

(3)

當軸承與軸碰撞時，嵌入深度為

δ=eij-c，

(4)

式中c為間隙大小，c=Ri-Rj，Ri和Rj分別為軸承和軸半徑。

體i,j的接觸點分別為Qi和Qj，基于絕對節點坐標法接觸點的全局位置為

(5)

全局坐標系下接觸點Qi和Qj的速度可以通過將式(5)對時間求導得到

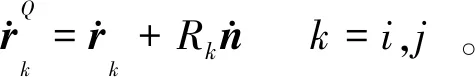
(6)

接觸點的法向相對速度vN和切向相對速度vT可表示為

(7)

(8)

式中切向量t通過向量n逆時針旋轉90°得到。

1.2 接觸碰撞力模型

Hertz接觸力模型是應用最廣泛的接觸力模型，該模型認為接觸表面為完全彈性碰撞，因此不能描述碰撞過程中的能量耗散。為了描述接觸碰撞過程中的能量損耗，基于Hertz模型，Lankarani，Herbert和Lee等提出了多種含能量耗散項的接觸碰撞力模型[14]。Liu等[15]研究發現Hertz接觸力模型僅僅適用于間隙相對較大且載荷較小的情況。對于小間隙情況，計算結果將無法滿足精度要求。針對上述問題，Bai等[16]構建了一種基于Lankarani-Nikravesh碰撞力模型和WEF(Winkler elastic foundation)模型的混合碰撞力模型，該碰撞力模型可以表示為

(9)

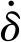
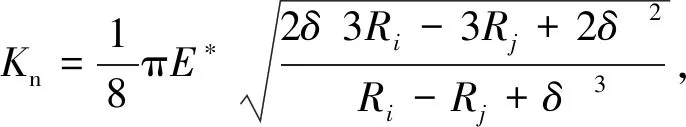
(10)

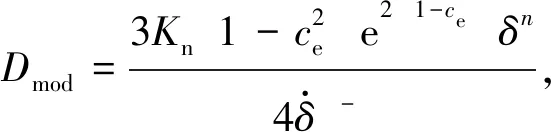
(11)

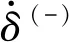
(12)

式中：vk(k=i,j)和Ek(k=i,j)分別是接觸材料的泊松比和彈性模量。該間隙碰撞力模型能夠普遍適用于大間隙和小間隙情況，通過與有限元仿真結果比較，該碰撞力模型的精度高于Hertz接觸力模型。

1.3 摩擦力模型

Coulomb摩擦模型是最簡單的摩擦力模型。該模型的摩擦力方向與切向速度方向相反，并且摩擦力大小與法向接觸力成正比。Coulomb摩擦模型在切向速度趨近于零時會產生不連續的摩擦力，這將有可能導致計算不收斂。為了解決該問題，Ambrsio[17]將速度引入Coulomb摩擦模型，建立了如下形式的摩擦力模型，

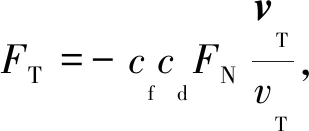
(13)

式中：cf為摩擦系數，vT為相對切向速度。cd為動態修正系數，可表示為

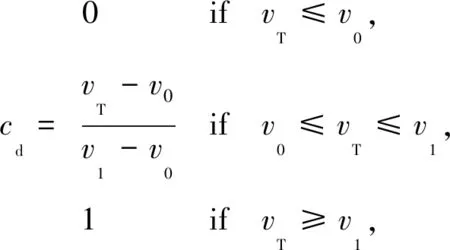
(14)

式中：v0和v1是為計算動態修正系數給定的速度極限值。Ambrsio摩擦力模型如圖2所示。

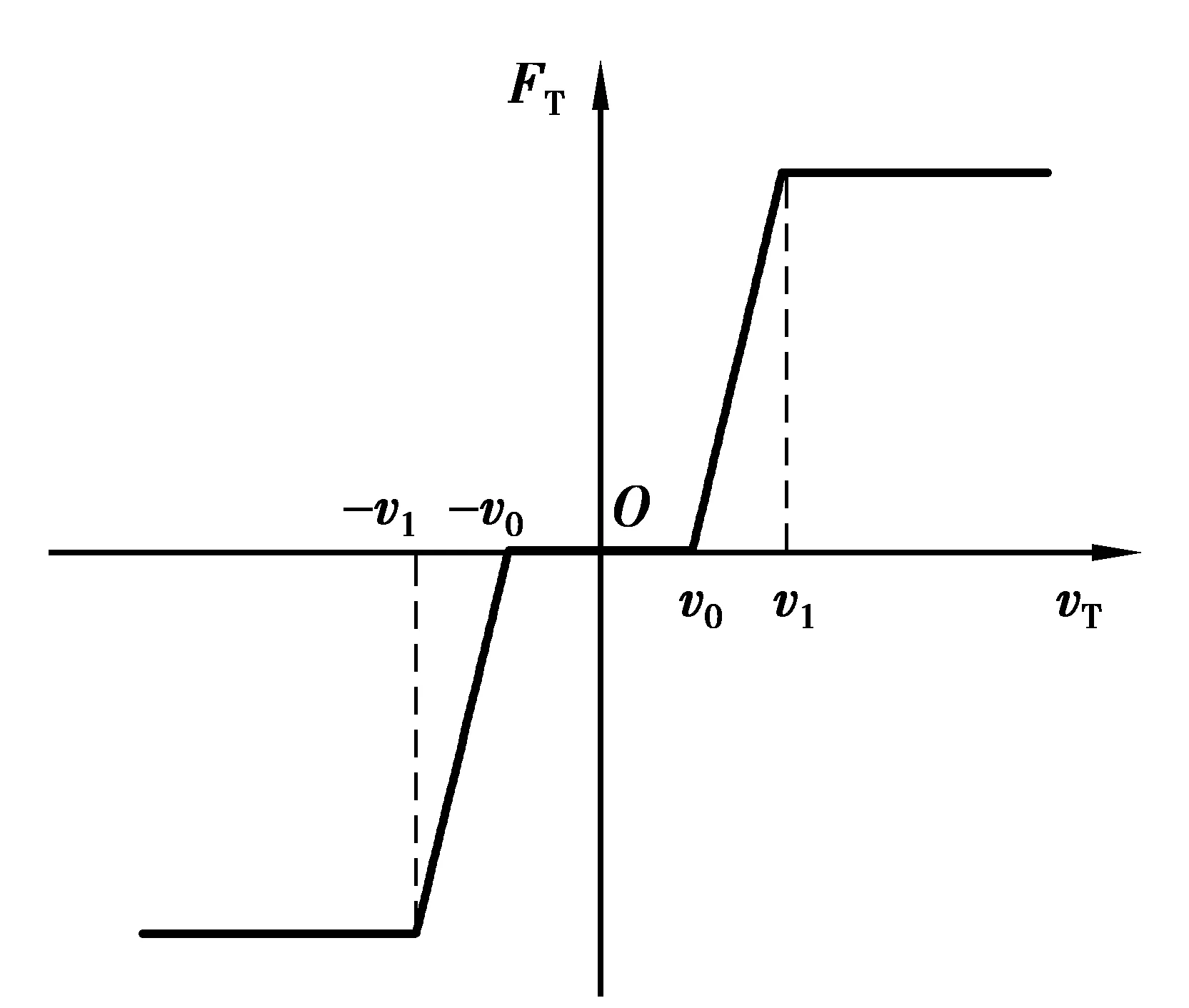
圖2 Ambrsio摩擦力模型Fig.2 Ambrsio friction model

2 含間隙柔性機械臂動力學建模

含間隙柔性機械臂模型如圖3所示。連桿OAi在O點處的運動副為理想平面轉動副，連桿OAi與連桿AjPj在A處的運動副為平面間隙轉動副。τ1和τ2分別為作用于連桿OAi和連桿AjPj的驅動力矩，n1和t1為連桿OAi在O點處的單位法向量和切向量，n2和t2為連桿OAi在Ai點處的單位法向量和切向量，n3和t3為連桿AjPj在Aj點處的單位法向量和切向量，θ1為連桿OAi在O點處的轉角，θ3為連桿OAi在Ai點處的轉角，θ2為連桿AjPj在Aj點處的轉角。考慮到運動過程中連桿OAi和連桿AjPj存在大變形，采用絕對節點坐標法對連桿OAi和連桿AjPj進行動力學建模。

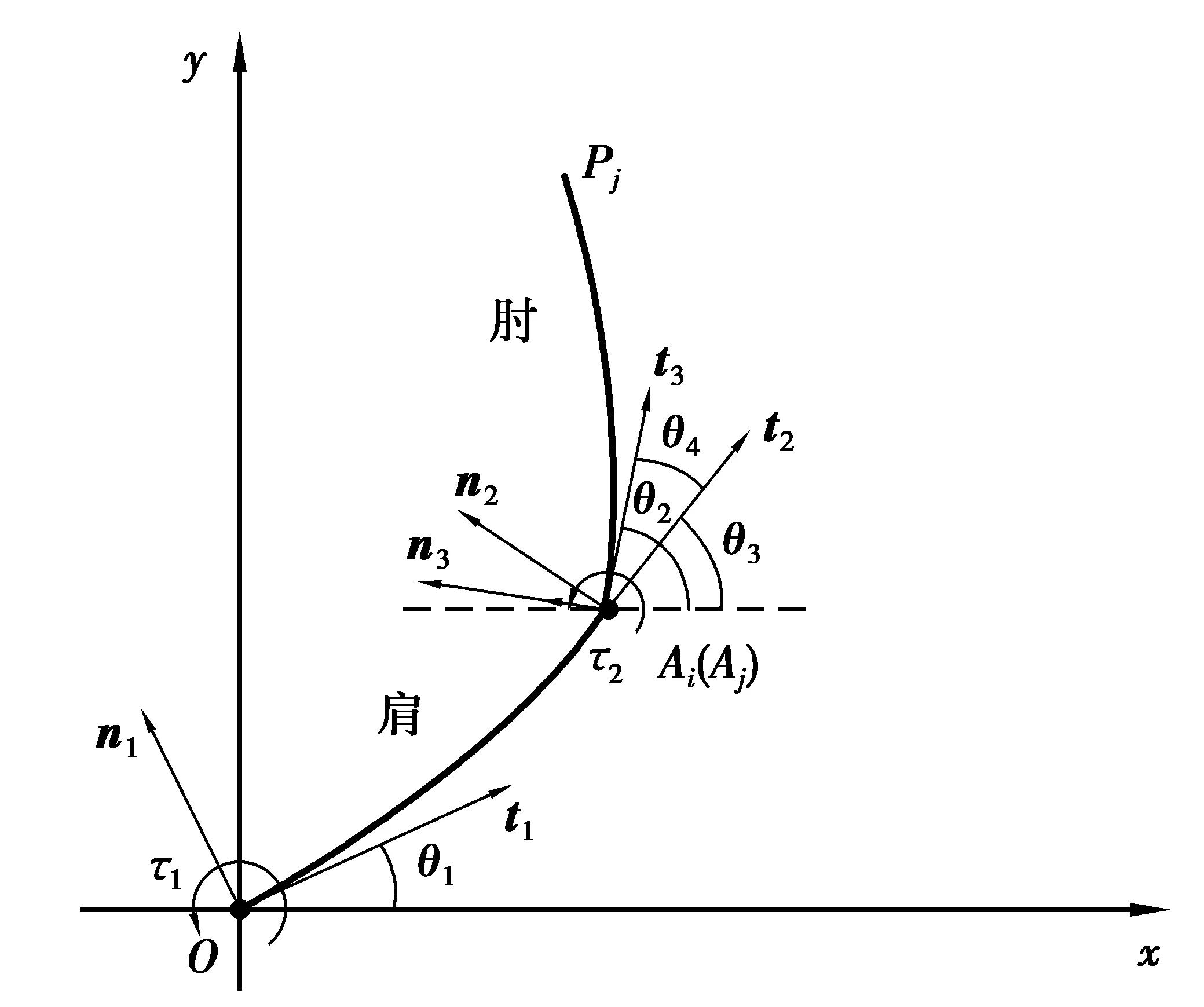
圖3 含間隙柔性機械臂Fig.3 Flexible manipulator with clearance

基于絕對節點坐標法[9]，平面梁單元上任意一點全局位置可表示

r=Sek，

(15)

式中S為由參數x決定的單元形函數，參數x∈[0l]表示未變形時特定點的軸向坐標，l為單元初始長度，單元形函數表示為：

(16)

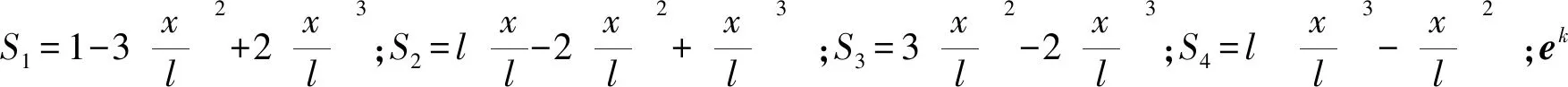
(17)

ri(i=m,n)表示節點i(i=m,n)位置矢量，?ri/?x(i=m,n)為節點i(i=m,n)的位置矢量對x方向的二維偏導數矢量。

基于上述描述，梁單元的動能可表示為

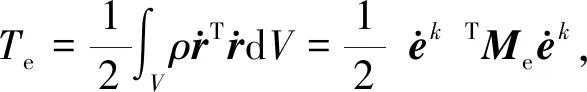
(18)

式中Me為梁單元的常數質量矩陣，可通過式(19)計算得到，

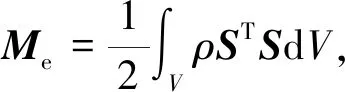
(19)

式中：ρ和V分別為單元密度和體積。

梁單元的彈性勢能可表示為

(20)

式中：σ和ε分別為應力矢量和應變矢量。

驅動力矩τ1和τ2所做的虛功可以表示為

δW=τ1δθ1+τ2δθ4=τ1δθ1+τ2δθ2-τ2δθ3。

(21)

對于一維兩節點柔性梁θ1的變分可以表示為

(22)

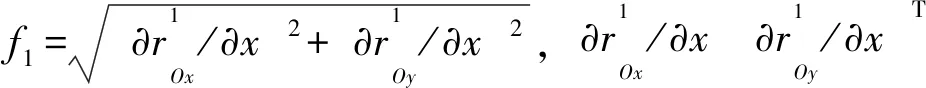
(23)

同理可以得到τ2的等效廣義力。基于虛功原理和Baumgarte方法[18]，該含間隙柔性機械臂的動力學方程表示為

(24)

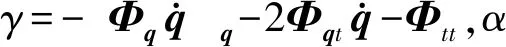
3 含區間鉸間隙柔性機械臂控制精度和動力學特性分析

由于材料不均勻、加工誤差、磨損等原因，機械臂廣泛存在不確定性，如間隙尺寸、部件楊氏模量等。這些不確定性因素會顯著的影響機械臂動力學特性和控制精度，考慮到間隙尺寸和楊氏模量數據的不完備性，這里將間隙尺寸和楊氏模量處理為區間變量，式(24)變為

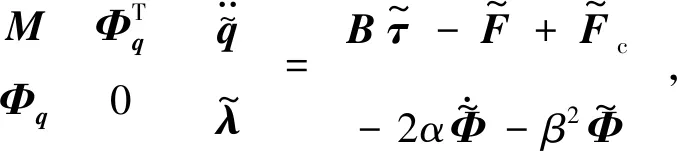
(25)

式中上標表示該值與區間變量(c,E)有關。式(25)為含區間不確定性變量和控制器的微分代數方程，對其進行求解將非常困難。這里將提出該動力學模型的求解方法，圖4列出了該方法的主要步驟，具體為：

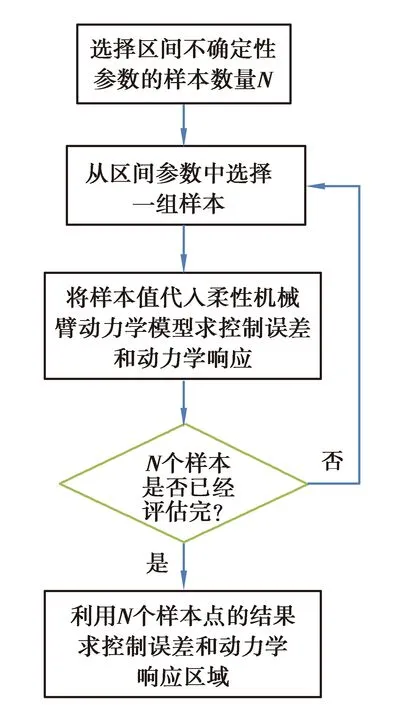
圖4 含區間鉸間隙柔性機械臂不確定性分析Fig.4 Uncertainty analysis of flexible manipulator with clearance

1)選擇區間不確定性的抽樣數量N。

2)從每一個區間參數中選擇一個樣本(ci,Ei)。

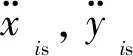
4)判斷區間不確定性的N個樣本是否已經全部分析。如果否，回到步驟(2)；如果是，繼續步驟(5)。

5)找出末端控制誤差、末端加速度和驅動力矩上邊界和下邊界，該上邊界和下邊界圍成的區域即為考慮區間不確定性時末端控制誤差、末端加速度和驅動力矩可能的區域。

4 仿真分析

該含間隙柔性機械臂末端點進行圓軌跡跟蹤控制，如圖5所示。連桿OAi和連桿AjPj長度分別為0.4 m和1.6 m。連桿OAi劃分為2個單元，連桿AjPj劃分為4個單元。連桿OAi和AjPj具有相同的截面形狀和材料參數，截面積為2.5×10-3m2，截面慣性矩為5.208×10-7m4，楊氏模量為30 GPa，密度為6 000 kg/m3。該機械臂的材料屬性及動力學分析相關參數如表1所示。仿真時間為10 s，跟蹤圓軌跡的角速度為

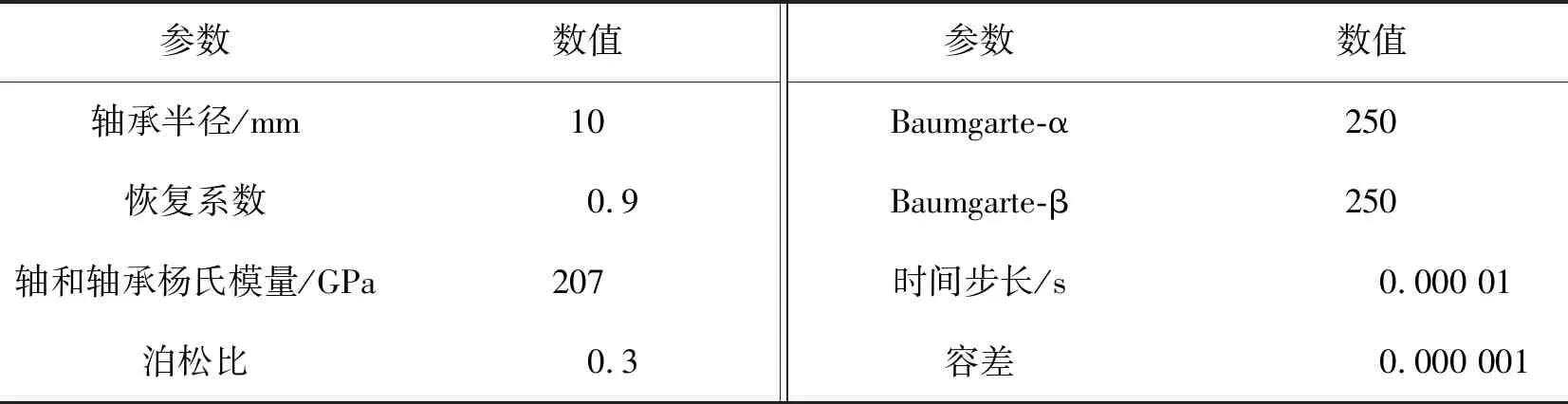
表1 機械臂仿真參數表Table 1 Simulation parameter table of manipulator

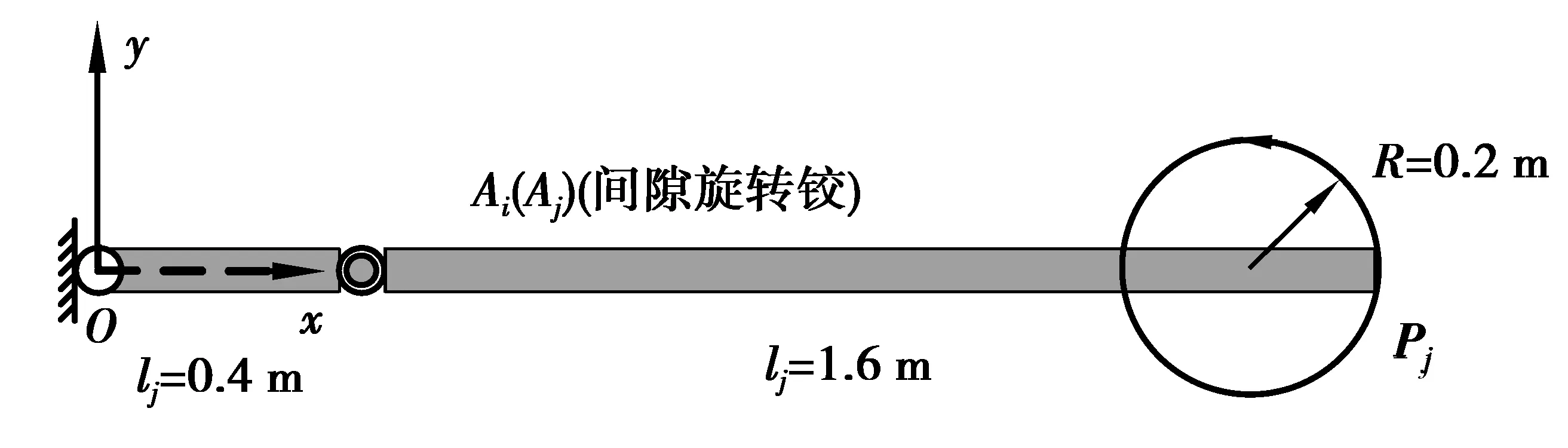
圖5 含間隙柔性機械臂末端圓軌跡跟蹤Fig.5 End circular tracking of flexible manipulator with clearance

(26)

為了研究間隙對機械臂動力學特性和控制精度的影響，分別取間隙c=0.01 mm，c=0.2 mm和c=0.5 mm，摩擦系數cf=0.1，將上述多種間隙情況計算得到的響應結果與理想鉸接副的響應結果進行比較。圖6為3種間隙情況下的末端控制誤差圖、末端加速度圖和驅動力矩圖。由圖6可知：當間隙大小為0.01 mm時，間隙對末端控制誤差、末端加速度和驅動力矩幾乎沒有影響；當間隙大小為0.2 mm和0.5 mm時，間隙對末端控制誤差的影響非常顯著，而且間隙越大控制精度越差；當間隙大小為0.2 mm和0.5 mm時，間隙對末端加速度和驅動力矩的影響依然不顯著。通過對圖7(d)進一步分析發現初始時刻機械臂末端y方向的加速度擴展較大，其原因在于：初始時刻間隙鉸中的軸與軸承存在劇烈碰撞，導致初始時刻機械臂末端y方向的加速度較大。

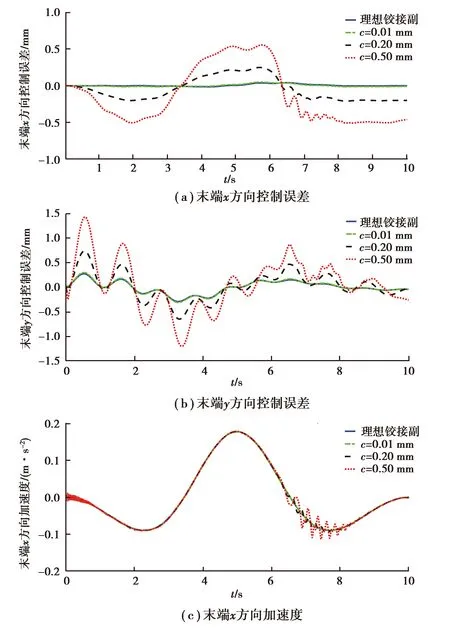
圖6 末端控制誤差、末端加速度和驅動力矩圖Fig.6 Tip error, tip acceleration and driving moment

為了分析部件柔性對機械臂動力學特性和控制精度的影響，取連桿楊氏模量為3，30，300 GPa，3種工況下的間隙c=0.5mm。末端控制誤差、末端加速度和驅動力矩如圖7所示。可以發現：當楊氏模量為3 GPa時，末端控制誤差、末端加速度和驅動力矩與楊氏模量為30 GPa的分析結果存在明顯差異，而且彈性模量較低時，末端劇烈抖動持續時間將增加；當楊氏模量為30 GPa和300 GPa時，兩種工況的末端控制誤差、末端加速度和驅動力矩差異不顯著。因此，當連桿彈性模量較小時，連桿柔性會顯著的影響控制誤差和機械臂的動力學特性，而連桿彈性模量較大時，連桿柔性對該機械臂的控制精度和動力學特性的影響將不顯著。

由于間隙尺寸和連桿柔性會顯著影響該機械臂控制精度和動力學特性，這里考慮間隙尺寸和楊氏模量為區間變量，其取值范圍分別為c=[0.1 0.5]mm，E=[20 30]GPa。采用本文中提出的方法對機械臂進行動力學特性和控制精度分析。末端控制誤差、末端加速度和驅動力矩如圖8所示。可以發現：考慮不確定性時，末端控制誤差將擴張，從而導致控制精度降低；末端加速度和驅動力矩也會擴展，從而影響該機械臂的動力學特性。

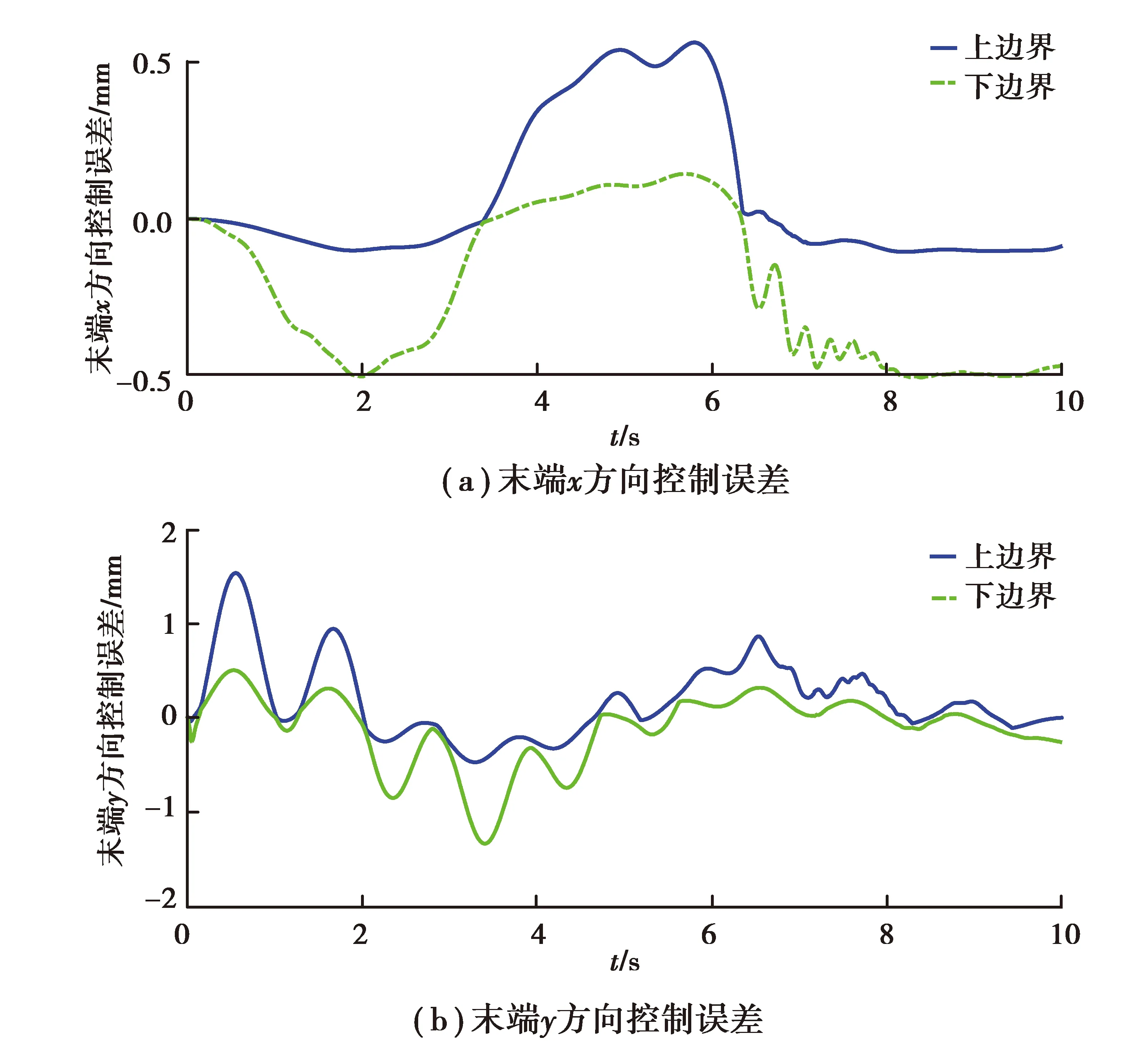
圖8 末端控制誤差、末端加速度和驅動力矩區域圖Fig.8 Upper and lower bounds of tip error, tip acceleration and driving moment

5 結 語

1)當間隙尺寸較小時，間隙對末端控制誤差、末端加速度和驅動力矩幾乎沒有影響。當間隙尺寸較大時，間隙對末端控制誤差的影響非常顯著，而且間隙越大控制精度越差。然而，較大間隙情況下，間隙對末端加速度和驅動力矩的影響依然不顯著。

2)部件柔性會顯著的影響末端控制誤差、末端加速度和驅動力矩。當部件彈性模量較低時，末端會劇烈抖動。

3)參數不確定性會顯著的降低該機械臂的控制精度，而且也會影響該機械臂的動力學特性。