新課程標準下的高考數學試卷對比分析（理科）

竇涵 韓旸

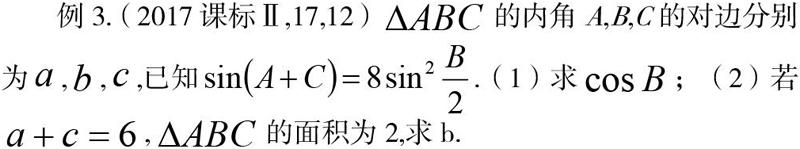
摘 要：高考試題一直是經典教學的議題，它為教育教學目標提供了核心指向，是進行教學問題設計的引領示范[1].高考試題難度也是教育工作者一直以來重點關注的話題之一.本文以2017-2019年高考數學全國卷Ⅱ（理科）為研究對象，運用層次分析法、統計法、加權平均法和綜合難度分析法，探析命題變化趨勢，以掌握新課標下數學學科的現狀，提出相應的教學策略，以便更好地從事教學工作，從而不僅能更好地指導教師根據不同層次的學生做到因材施教，還能使學生從真題中明確學習目標和方向，做出有針對性的學習方案.

關鍵詞：層次分析;加權平均 ;試卷分析

在新時代背景下，全國高考改革也面臨著新任務，如何在新的體系中發揮試卷分析的優勢，進一步為教育改革服務，已經越來越成為人們關注的熱點問題.本文以2017-2019年新課程標準的改革對近年來高考試題所產生的影響為背景，以近三年高考數學全國卷Ⅱ（理科）為研究對象，對試卷結構和試題綜合難度進行了對比分析[2]，把握命題趨勢.從試卷的命題角度，考點對應分值分布等進行對比研究試卷特點.

一、理論基礎

高考是基礎教育和高等教育銜接的橋梁，是基礎教育改革以及選拔人才的重要環節和途徑，是教師檢驗教學成果和學生展現學習水平的重要方式，高考試題分析已然成為眾多教育工作者重點關注的問題.通過研究2018和2019年江蘇高考卷發現：數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析等6個數學核心素養具體表現的考查分布極不均衡，數學運算（特別是法則運用）、邏輯推理（特別是演繹推理）的考查較多，而部分核心素養和具體表現極少考查甚至從未考查（如問題提出、合情推理等）.

二、三套全國卷考點對比分析

在近三年的試卷中所涵蓋的高中知識點非常全面，無論是對基礎知識的考查還是對實際應用能力的拓展，都在不同程度上體現了新課程標準的要求，導向作用較好，重難點突出，可以看出高考命題不但展現出新穎的命題思路，做到與時俱進，而且對知識點的考查比較穩定，綜合難度也呈穩定趨勢，符合各層次學生學習.其次，從試題的知識點分布情況看，試題中基礎知識所占分值比較大，例如函數、三角圓、橢圓、雙曲線、拋物線以及復數的計算、導數的計算、立體幾何等方面進行命題.

三、試卷特點分析

1. 題型靈活，技巧性強

在近三年的全國卷Ⅱ中幾乎每年都有對集合的運算考查，同時也十分重視對三視圖、程序框圖等空間以及思維能力的考查，并在試題難度上進行了合理把控，降低了解題難度和減少了運算步驟，使考生能夠減短做題時間.

例1.（2019年課標Ⅱ，1，5）設集合，則

例1是以集合的交集為載體，主要考察了學生的運算能力以及求解能力;突出了高考命題對學生數學運算能力的素養提出的要求，學生在掌握一定的計算技巧后，可以靈活的將此類問題化繁為簡，化難為易，縮短做題時間.

2.應用性強，重視數學思維的考察

學生能否順利靈活地將課堂所學知識應用到實際生活中，關鍵在于能否把實際問題抽象化、簡單化，并能有效對應知識點去解決問題，近年的全國Ⅱ卷就將此類實事應用作為熱點議題，無論是2017年的“《算法統宗》”，還是2019年1月3日“嫦娥四號的成功著陸”，無不是站在弘揚中華文化，秉承民族特色的角度去關注社會熱點，直面現實生活，賦予數學試題更多的人文內涵.

例2.（2017年的課標Ⅱ，3，5）我國古代數學名著《算法統宗》中有如下問題：“遠望巍巍塔七層，紅光點點倍加增，共燈三百八十一，請問尖頭幾盞燈？”意思是：一座7層塔共掛了381盞燈，且相鄰兩層中的下一層燈數是上一層燈數的2倍，則塔的頂層共有燈（?）

A.1盞?B.3盞?C.5盞?D.9盞

上述例2是我國古代數學名著《算法統宗》中的問題，在突出我國博大精深的傳統文化的同時，也考察了學生對已知條件的概括能力;充分體現了數學的應用性，讓學生關注社會熱點，同時增加了學生的民族自信心、自豪感.

3.綜合性強，注重基礎

高中數學教材中有大量的例題及基礎練習題，學生在多次的考試及測試中不難發現，無論是平時的期末考，還是模擬考，亦或是高考真題，均在基礎知識的考查上所占分值甚高，高考真題中部分題目只是將教材中的例題描述更加抽象化，在解題形式上更加綜合化，并注重與生活的結合，做到將真題回歸教材，提升教材在學習中的地位.

上述例3是在學生充分掌握三角形內角和性質的基礎上，考察學生對三角函數的誘導公式以及正弦和余弦平方關系的應用，又進一步考察了三角函數與三角形面積的關系，學生在學習三角函數時要注重與三角形、圓等幾何形狀相結合，此類問題便會迎刃而解;不難發現，高考在命題中越來越側重于對學生的概括能力、邏輯思維能力以及綜合運用能力的考察.

四、教學啟示

1.增強學生思維能力，提高運算能力

在高中數學學習中，隨著學習知識的不斷深化，計算難度也隨之增加，于是學生在計算過程中所顯露出的問題也隨之增多.在教學過程中，通過案例分析發現，造成學生操作錯誤的因素至少有三個： 一是書寫錯誤，常會出現對題干誤讀或抄寫錯誤的情況; 二是公式、定理、定義、規則記憶不準確，理解不深入，使用不靈活.三是學生在解答問題時過程書寫不規范，思維遷移能力不夠靈活.所以，在教學中，教師應重點重視對學生計算能力的考察，加強學生的思維訓練，關注細節，讓學生在平時便養成良好的書寫習慣，提高學生的運算能力.

2.注重知識的遷移，提高思維能力

數學的學習重在是否能將所學知識靈活運用，是分散的知識點運用發散性的邏輯思維進行串聯，從而更加簡便的解決問題.數學思維能力的形成和提高是一個循序漸進的過程，需要在總體復習中逐步發展和完善.因此，在全面復習和鞏固所學知識的同時，更應該注重學生對知識的應用情況，加強學生對綜合能力的培養，特別是要重視學生的創新意識和實踐能力，不斷提高學生的數學素質，從而適應高考的新要求.

3.鞏固基礎，回歸教材

隨著高考改革的不斷推進，基礎知識在高考試卷中所占的比重越來越大，回歸教材，加強基礎知識的培養已經成為每位教師應當注重的問題.高中數學基礎知識主要是指數學的概念和原理，而高考主要考察學生對高中數學基礎知識的掌握情況以及在解題過程中所蘊含的解題思想、方法等.因此，鞏固基礎知識不僅是在復習以前學過的知識，更要以主線知識，使學生熟練掌握每一點知識的內涵和外延，從而提高學生數學學習能力.

五、結論

本文以2017-2019年高考數學全國卷Ⅱ（理科）試題為研究對象，研究發現試題的設計更加側重學生面對復雜問題時的思考能力，以及培養學生精準提煉信息分析問題、處理問題的能力.分析表明高考試卷不僅注重考查學生的基礎知識和基本技能，更加從人才培養的高度思考學生的各素養.因此，加強對命題技術的研究，力圖全面考察學生的學科素養，在教學中關注對學生的理性思維的考查，注重知識的靈活運用[3]鞏固基礎，回歸教材，突出數學教學本質，從而培養學生的綜合素養.

參考文獻

[1] 季景葉.基于江蘇高考試卷分析的課堂教學啟示[J].思想政治課教學，2019（12）：73-75.

[2]張怡，武小鵬，彭乃霞.綜合難度系數模型在2016年高考數學試題評價中的應用[J].教育測量與評價，2016（12）：47-53.

[3] [4] 中共中央辦公廳，國務院辦公廳.關于深化新時代學校思想政治理論課改革創新的若干意見[Z].2019-08-14.

作者簡介：竇涵（1997-），女，黑龍江哈爾濱人，在讀碩士研究生，從事數學教學研究

通信作者：韓旸（1969-），男，黑龍江齊齊哈爾人，教授，從事數學教育教學研究.

（齊齊哈爾大學 理學院?黑龍江?齊齊哈爾?161006）