齒根安全條件下多狀態嚙合齒輪傳動系統安全-吸引盆侵蝕與分岔

李正發，茍向鋒，朱凌云，石建飛，尹 樁

(1.天津工業大學 機械工程學院，天津 300387；2.天津工業大學 天津市現代機電裝備技術重點實驗室，天津 300387)

齒輪傳動廣泛應用于機械系統中，輪齒折斷是其主要失效形式之一。對齒輪傳動系統安全特性的研究相對于穩定周期解更貼近工程實際。安全盆是研究非線性系統全局安全特性的重要方法，其安全條件的建立至關重要。

吸引子和吸引域有助于研究非線性系統的全局特性。張瑩等[1]運用吸引子和吸引域對二維離散Duffing 映射系統的全局動力學進行了研究。唐進元等[2]用一種改進的圖胞映射算法，研究了單自由度齒輪系統的吸引子、吸引域和不穩定解的全局特性。Lu等[3]研究發現，單自由度齒輪系統不同周期運動的吸引子具有相對穩定的吸引區域，當系統的擾動達到一定值才會明顯改變系統解的拓撲結構。Gou等[4]提出一種改進胞映射算法，計算了單自由度齒輪系統的吸引子，分析了其吸引域轉遷過程；茍向鋒等[5]借助多初值分岔圖、吸引域圖分析了參數耦合對系統動態特性的影響規律。

安全盆理論自Thompson等提出以來，廣泛應用于非線性系統安全特性的研究。Long等[6]用安全盆理論和Monte Carlo法預測了自由海域中船舶的生存概率。ücer等[7]運用安全盆理論對BSRA拖網漁船的穩定性進行研究，得到了安全盆中的安全點和不安全點。葛根等[8]研究了白噪聲激勵和簡諧激勵下形狀記憶合金梁的安全盆侵蝕。尚慧琳等[9]研究了時滯位置反饋對一類非線性相對轉子系統的混沌運動和安全盆侵蝕控制。Gong等[10]研究了弱參數周期擾動對非線性振蕩器安全盆的影響。劉志亮等[11]用一種確定安全盆中安全域邊界的懲罰參數選擇算法，研究滾動軸承的安全域。Wei等[12]研究了白噪聲對電力系統安全盆侵蝕的影響，但只考慮了不安全區域對安全區域的侵蝕。

目前對安全盆的研究中，通過判斷考察區域內初值點經過長時間迭代后是否逃離給定安全區域，確定考察區域內的不安全點和安全點。由于未建立安全條件和分辨安全盆中的吸引子共存，所得安全盆中僅有安全域和不安全域，未研究安全盆中不同周期運動吸引域之間的侵蝕與分岔過程。

本文通過計算齒根彎曲應力，結合齒根許用彎曲應力建立齒根的安全條件。采用四階Rung-Kutta法數值計算系統在考察區域內隨參數變化時的吸引盆及其演變過程。判斷吸引盆中不同運動類型吸引域在齒根安全條件下的安全特性，獲得多狀態嚙合齒輪傳動系統齒根安全條件下的安全-吸引盆。借助吸引子、多初值分岔圖和最大Lyapunov指數圖(TLE)分析系統安全-吸引盆的分岔與侵蝕過程。

1 單級齒輪傳動系統多狀態動力學模型

圖1 齒輪系統簡化物理模型Fig.1 Simplified physical model of the gear system

表1 齒輪副的系統參數

齒側間隙使得系統會出現齒面嚙合、輪齒脫嚙和齒背接觸等多種嚙合狀態。圖2為齒面嚙合、輪齒脫嚙和齒背接觸時的嚙合狀態示意圖。齒面嚙合時，齒輪m為主動輪p，齒輪n為從動輪g；齒背嚙合時相反。N1N2為齒面嚙合線，M1M2為齒背接觸線。Rpi、Rgi(i=1、2)為主動輪p、從動輪g中第i對嚙合輪齒上嚙合點到齒輪中心的距離。

(a) 齒面嚙合(b) 輪齒脫嚙

(c) 齒背接觸圖2 系統嚙合狀態示意圖Fig.2 Schematic diagram of system engagement state

Shi等[13-14]建立了考慮齒面摩擦、時變嚙合剛度、嚙合阻尼、齒側間隙和綜合傳遞誤差的單級齒輪傳動系統多狀態動力學模型

Fm+εω2cos(ωt)

(1)

式中:x為輪齒的相對位移;“·”表示對時間求導;ξ為無量綱阻尼;k為無量綱嚙合剛度波動幅值;ω為無量綱嚙合頻率;ε為無量綱綜合傳遞誤差幅值;Fm為負載。M(t)可按式(2)計算得到

(2)

式中:Spi(t)、Sgi(t)(i=1,2)分別為主、從動輪中第i對嚙合輪齒的摩擦力臂。齒面嚙合時(圖2(a))，Spi(t)為第i對嚙合輪齒上的嚙合點到N1的距離，Sgi(t)為第i對嚙合輪齒上的嚙合點到N2的距離。齒背接觸時(圖2c)，Spi(t)為第i對嚙合輪齒上的嚙合點到M1的距離，Sgi(t)為第i對嚙合輪齒上的嚙合點到M2的距離。Spi(t)、Sgi(t)可由式(2)計算得到。

(3)

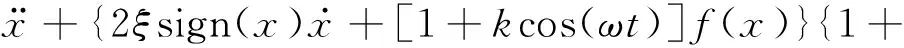
μ[Y1(t)g1(t)sign(Vs1(t))+

Y2(t)g2(t)sign(Vs2(t))]}=Fm+εω2cos(ωt)

(4)

式中，摩擦因數μ=0.05。定義sign(x)函數區分齒面嚙合和齒背接觸時阻尼力的方向。

(5)

齒側間隙函數f(x)定義如下

(6)

式(5)、(6)中，D為無量綱齒側間隙的一半。

根據文獻[15]，式(4)中第i(i=1、2)對嚙合輪齒的載荷分配率函數Yi(t)按以下兩種情況分別計算。

當nT0≤t≤(εa-1)nT0(雙齒嚙合)時

(7)

當(εa-1)nT0≤t≤(n+1)T0(單齒嚙合)時

(8)

式(4)中由于嚙合輪齒的相對滑動速度導致摩擦力的方向改變，當相對滑動速度為0時,摩擦力為0。定義摩擦力方向函數sign(Vsi(t))

(9)

式中，第i對嚙合輪齒的相對滑動速度Vsi(t)

Vsi(t)=ωpRpi(t)sinαmpi(t)-ωgRgi(t)sinαmgi(t)

(10)

其中，Rpi(t)、Rgi(t)(i=1,2)可由式(11)計算得到。

(11)

式(10)中，αmpi(t)、αmgi(t)(i=1,2)為主動輪p、從動輪g中第i對嚙合輪齒上嚙合點的壓力角

(12)

(13)

2 防止齒根折斷安全條件的建立

以齒輪m為研究對象，嚙合輪齒的齒根許用彎曲應力可由式(14)計算得到[16]。

σFP=σFEYNTYδreltYRreltYX/SFmin

(14)

MQ級氣體滲氮處理調質鋼的參數為：σFE=580 MPa，YNT=1.01，Yδrelt=1.0，YRrelt=0.9，YX=1,SFlim=1.2。則齒根許用彎曲應力σFP=440 MPa。

由式(13)可得嚙合過程中齒輪m所受無量綱動態嚙合力

(15)

(16)

考慮齒輪嚙合過程中的單雙齒交替嚙合，第i(i=1、2)對嚙合輪齒所受沿嚙合線方向的嚙合力Fni

Fni=FnYi(t)

(17)

圖3 齒輪的時變嚙合剛度Fig.3 Time-varying meshing stiffness of gears

選取系統參數ω=1.4，ε=0.2，ξ=0.05，k=0.18，D=0.5，μ=0.05，Fm=0.23。以x1=1.174 286,x2=0.334 286為初值計算得到系統相圖，如圖4(a)所示。圖中虛線為|x1|=D=0.5。相軌跡位于x1=0.5右側時，系統齒面嚙合，齒輪m受沿N2N1方向的嚙合力；相軌跡位于兩條虛線之間時，輪齒脫嚙；相軌跡位于x1=-0.5左側時，系統齒背接觸，齒輪m受沿M1M2方向的嚙合力。同組參數下計算齒輪m嚙合過程中的Fn、Fn1和Fn2，如圖4(b)所示。圖4(c)為圖4(b)在C方向的放大圖。圖4(b)、(c)中的黑色虛線為Fn、黑線為Fn1、灰色線為Fn2。相軌跡位于x1=0.5右側時，Fn>0；相軌跡位于兩條虛線之間時，Fn=0；相軌跡位于x1=-0.5左側時，Fn<0。圖4(b)、(c)中，當Fn=Fn1∪Fn2=0時(黑色虛線和黑線重合，灰色線等于0)，系統單齒嚙合；當Fn=Fn1+Fn2時(黑色虛線、黑線和灰色線均不等于0)，系統雙齒嚙合。需要注意的是，圖4(b)、(c)中存在T和T0兩個時間尺度。其中，T=2π/ωm為嚙合周期，T0=2π/(Zmωm)為完成一次單、雙齒交替嚙合的時間。

圖4(b)中的黑色虛線先由Fn>0→Fn=0→Fn<0→Fn=0。Fn>0時，系統為齒面嚙合狀態；當Fn逐漸減小到0后，沿負方向增加(時間區間較小)，最后突變為0，見圖4(b)中的A區域。此時，系統由齒面嚙合變為脫嚙。當Fn=0時，系統為脫嚙狀態。之后，圖4(b)中的黑色虛線經由Fn=0→Fn>0→Fn=0→Fn<0。Fn由0突變為正，然后逐漸減小為0并向負方向增加(時間區間較小)，見圖4(a)中的B區域，輪齒脫嚙變為齒背接觸。當Fn<0時，系統為齒背接觸狀態。圖4(b)中嚙合點1、2上所受的嚙合力Fn1≠Fn2，任意時刻嚙合齒對1和嚙合齒對2上所受的齒根彎曲應力不相等，應分別計算嚙合輪齒1和嚙合輪齒2上的齒根彎曲應力。

(a) 相圖(b) 嚙合力時間歷程圖

(c) C方向放大圖圖4 相圖、隨t變化的Fn、Fn1、Fn2Fig.4 Phase diagrams and values of Fn、Fn1、Fn2 via t

齒面摩擦力在節圓附近改變方向。以節圓為界將嚙合區分為兩部分：節圓至齒根圓為下嚙合區，節圓至齒頂圓為上嚙合區。圖5中齒根圓角半徑r=0.38m；點Bi(i=1,2)為齒輪m中嚙合輪齒i上的嚙合點。嚙合輪齒受到法向力Fni和齒面摩擦力Ffi。Fni沿法線方向延伸交輪齒中線于Ai點，Ffi沿切線方向交輪齒中線于Ci點。根據弦切法可得危險截面H1H2。Li為Ai到H1H2的距離，ΔLi為Ai到Ci的距離。Fni和Ffi沿齒高方向上的分力在齒根危險截面產生的拉壓應力很小[20]，故不考慮其對齒根彎曲應力的影響。齒面摩擦力為

Ffi=Fniμ

(18)

(a) 下嚙合區輪齒受力圖(b) 上嚙合區輪齒受力圖圖5 嚙合輪齒受力圖Fig.5 Force diagram of the meshing teeth

齒根危險截面H1H2受到的彎曲應力可由式(19)、(20)計算得到。其中，雙齒嚙合時

(19)

單齒嚙合時

(20)

為使計算得到的σFi(t)能夠更清晰地反應系統的嚙合狀態，將圖4中的Fn1和Fn2代入式(18)～(20)計算得到圖6(a)。圖中黑線代表σF1，灰色線代表σF2。圖6(a)中，σFi>0時齒面嚙合；σFi=0時輪齒脫嚙；σFi<0時齒背接觸。圖6(b)為圖6(a)中C方向的放大圖。圖中σF1≠0、σF2≠0時，系統處于雙齒嚙合狀態；σF1≠0、σF2=0時，系統處于單齒嚙合狀態。圖6(b)中嚙合點處于單齒嚙合區時，齒根危險截面上的彎曲應力最大；摩擦力在節圓附近的方向變化引起圖6(b)中黑線σF1在單齒嚙合區存在突變。圖6(c)為圖6(a)中某一輪齒從進入嚙合到脫離嚙合過程中的齒根彎曲應力圖。

(a) 齒根彎曲應力時間歷程圖(b) C方向放大圖

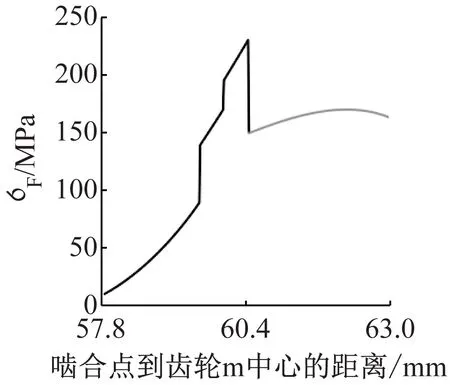
(c) 嚙合輪齒齒根彎曲應力圖圖6 隨t變化的σF1、σF2和嚙合輪齒齒根彎曲應力圖

齒輪在齒根彎曲應力大于齒根許用應力下長時間運行，會出現齒根彎曲疲勞，嚴重時發生輪齒折斷；據此可建立齒根不發生彎曲疲勞的安全條件

σFi≤σFP

(21)

在安全盆中，以不同吸引子為初值獲得系統不同的運動狀態，計算不同運動狀態下齒輪1中嚙合輪齒的齒根彎曲應力(雙齒嚙合時σF1(t)、σF2(t)；單齒嚙合時σF1(t)、σF2(t)=0)，并與齒根許用彎曲應力σFP比較。當存在σFi(t)≥σFP時，該吸引子及其吸引域不安全；反之，該吸引子及其吸引域安全。

3 齒根安全條件下系統安全-吸引盆侵蝕與動力學分析

采用單一變量法，分別研究負載Fm和齒側間隙D變化時系統的全局動力學和安全特性。利用吸引子和第二節建立的齒根安全條件對考察區域Hi內吸引域的安全特性進行考察，獲得系統的安全-吸引盆；利用多初值分岔圖和TLE分析安全-吸引盆的侵蝕與分岔過程。

3.1 參數Fm變化下安全-吸引盆的侵蝕與分岔

取系統參數ω=1.4，ε=0.2，ξ=0.05，k=0.18，D=0.5，μ=0.05。在系統響應的相空間中選擇考察區域H1∈{-2≤x1≤2,-2≤x2≤2}。圖7為系統隨Fm減小時安全-吸引盆的侵蝕與分岔過程。圖中不同形狀的點代表不同運動類型的吸引子，吸引子的個數代表周期數；不同顏色區域為該吸引子的吸引域。Pn代表周期數，U代表該吸引域不安全，S代表該吸引域安全。圖8為以新出現或數量變化的吸引子為初值計算得到的σFi(t)；其中黑線為σF1(t)，灰色線為σF2(t)，黑色虛線為安全邊界σFP=440 MPa。

表2列出了Fm∈(0.1,0.35)逐漸減小時系統安全-吸引盆中吸引子的共存情況和演變過程。當Fm∈(0.290 3,0.35)，安全-吸引盆中只存在安全吸引子P1，圖7(a)為Fm=0.3時系統的安全-吸引盆，橙色區域為P1吸引子的吸引區域，以P1吸引子x1=0.46,x2=0.065 714為初值計算得到圖8(a)，圖中黑線和灰色線均未超過440 MPa，即齒輪嚙合過程中σFi始終小于σFP，可判斷橙色區域為安全區域，將其標為P1S。

當Fm減小至Fm=0.290 3時，安全-吸引盆中出現不安全吸引子P21，橙色區域P1S中部分初值進入P21吸引子的吸引區域，安全-吸引盆中出現新的吸引域，安全-吸引盆發生分岔。當Fm∈(0.269 9,0.290 3]時，安全-吸引盆中P1和P21共存。圖7b為Fm=0.27時系統的安全-吸引盆，藍色區域為P21吸引子的吸引域，以P21吸引子x1=0.682 857,x2=0.785 714為初值計算得到圖8(b)。圖中黑線超過黑色虛線，即齒輪嚙合過程出現σFi>σFP，可以判斷藍色吸引域為不安全區域，將其標為P2U1。

表2 隨Fm減小系統吸引子的演變過程

當Fm=0.269 9時，安全-吸引盆中出現不安全吸引子P22，P2U1藍色區域中部分初值進入P22吸引子的吸引區域，當Fm∈(0.185 8,0.269 9]時，安全-吸引盆中P1、P21和P22共存。圖7(c)為Fm=0.23時系統的安全-吸引盆，紅色區域為P22吸引子的吸引域，以P22吸引子x1=1.174 286,x2=0.334 286為初值計算得圖8(c)，可以判斷紅色區域為不安全區域，將其標為P2U2。圖7(d)為Fm=0.2時系統的安全-吸引盆，其中未發生吸引區域的出現或消失，橙色區域和紅色區域的面積逐漸減小，藍色區域的面積逐漸增大，該過程中安全-吸引盆發生侵蝕。

當Fm=0.185 8時，安全吸引子P1分岔為安全吸引子P2。Fm∈(0.178,0.185 8]時，安全-吸引盆中P2、P21和P22共存。圖7(e)為Fm=0.182時系統的安全-吸引盆，橙色區域變為P2的吸引區域，以P2吸引子x1=0.265 714,x2=0.031 429為初值計算得圖8(d)，藍色區域為安全區域，標為P2S。

當Fm=0.178時，安全-吸引盆中出現不安全吸引子P6，P2U1藍色區域中部分初值進入P6吸引子的吸引區域。當Fm∈(0.173 7,0.178]時，安全-吸引盆中P2、P21、P22和P6共存。圖7(f)為Fm=0.175時的安全-吸引盆，圖中紫色區域為P6吸引子的吸引區域。以P6吸引子x1=-0.134 286,x2=0.431 429為初值計算得圖8e，紫色區域為不安全區域，記為P6U。

當Fm=0.173 7時，安全-吸引盆中出現不安全吸引子PN，P6U紫色區域中部分初值進入PN吸引子的吸引區域。Fm∈(0.165,0.173 7]時，安全-吸引盆中P2、P21、P22、P6和PN共存。圖7(g)為Fm=0.17時系統的安全-吸引盆，圖中黃銅色區域為PN的吸引區域。以PN吸引子x1=0.077 14,x2=-0.785 71為初值計算得圖8(f)，黃銅色區域為不安全區域，記為PNU。當Fm∈(0.164 4,0.165)時，P1和PN吸引子的吸引區域不斷減小，當Fm=0.164 4時，安全-吸引盆中橙色區域P2S及其吸引子P2消失，PNU消失。Fm∈(0.158 7,0.164 4]時，安全-吸引盆中P21、P22和P6共存，圖7(h)為Fm=0.163時的安全-吸引盆。

(a) Fm=0.3(b) Fm=0.27

(c) Fm=0.23(d) Fm=0.2

(e) Fm=0.182(f) Fm=0.175

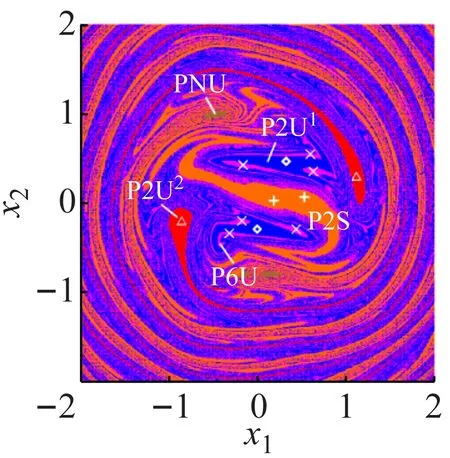
(g) Fm=0.17(h) Fm=0.163

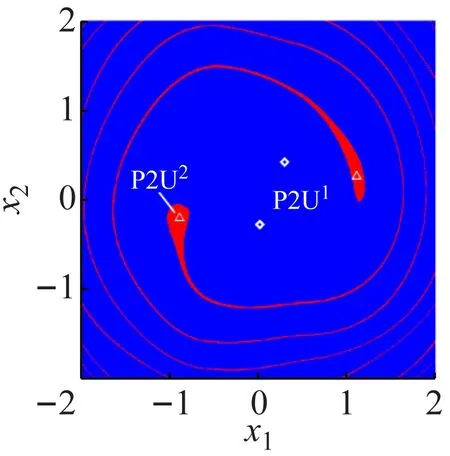
(i) Fm=0.156(j) Fm=0.147

(k) Fm=0.13圖7 系統安全-吸引盆隨Fm的侵蝕與分岔過程Fig.7 Erosion and bifurcation of safe basins of system via Fm

當Fm=0.158 7時，紫色區域P6U及其P6吸引子消失。當Fm∈(0.153 9,0.158 7]時，安全-吸引盆中P21和P22共存，圖7(i)為Fm=0.156時的安全-吸引盆。當Fm=0.153 9時，不安全吸引子P21分岔為安全吸引子P4，當Fm∈(0.143 5,0.153 9]時，安全-吸引盆中P4和P22共存。圖7(j)為Fm=0.147時的安全-吸引盆，以P4吸引子x1=0.557 143,x2=0.391 429為初值計算得圖8(g)，藍色區域為安全區域，記為P4S。

當Fm=0.143 5時，藍色區域安全吸引子P4分岔為安全吸引子PN，當Fm∈(0.1,0.143 5]時，安全-吸引盆中P22和PN共存。圖8(k)為Fm=0.13時的安全-吸引盆，以PN吸引子x1=-0.077 143,x2=0.031 429為初值計算得圖8(h)，該吸引子的吸引區域為安全區域，記為PNS。

(a) Fm=0.3(b) Fm=0.27

(c) Fm=0.23(d) Fm=0.182

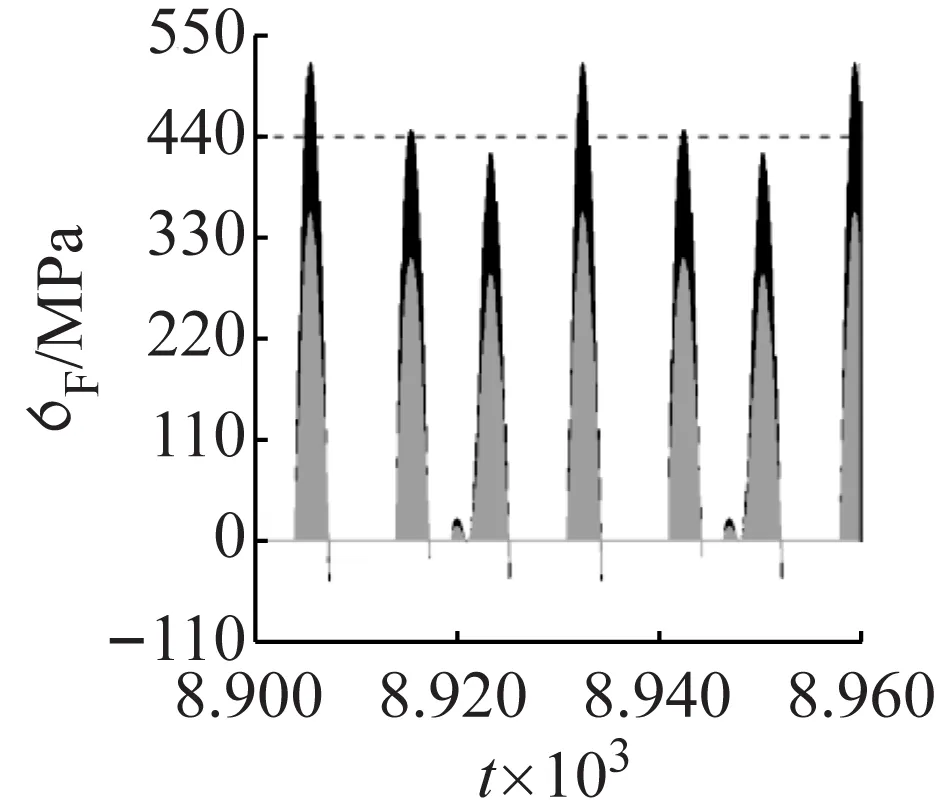
(e) Fm=0.175(f) Fm=0.17

(g) Fm=0.147(h) Fm=0.13圖8 隨t變化的σF1和σF2；圖中黑線為σF1，灰色線為σF2

綜上所述，由于齒輪系統對初值的敏感性，不同的初值會得到不同的吸引子，且不同吸引子引起的齒根彎曲應力不同。隨著負載Fm減小，圖7中相同顏色吸引域下的齒根彎曲應力逐漸減小。如，圖7中橙色吸引域由P1S變為P2S時，其引起的齒根彎曲應力由圖8(a)減小為圖8(d)；圖7中藍色吸引域經過P2U1→P4S→PNS，其引起的齒根彎曲應力變化經過圖8(b)、圖8(g)及圖8(h)，藍色吸引域下的齒根彎曲應力由不安全減小為安全。當Fm∈(0.290 3,0.35)時，安全-吸引盆只存在安全吸引子P1及其吸引域，如圖7(a)所示；當Fm等于0.290 3、0.269 9、0.178、0.173 7時，安全-吸引盆中出現不安全吸引子P21、P22、P6、PN及相應的吸引域，安全-吸引盆的安全性和穩定性變差。Fm在一定范圍內減小時，安全-吸引盆中內P21、P22、P6、PN吸引子的吸引域面積逐漸增大，引起安全-吸引盆中不安全區域的面積增大，安全區域的面積減少。因此Fm和初值共同影響系統的全局安全特性。

在某參數下，安全-吸引盆中吸引子的類型或數量改變，導致安全-吸引盆中吸引域的共存情況發生變化，引發安全-吸引盆分岔。某參數范圍內，安全-吸引盆中吸引子的類型和數量沒有變化，未出現吸引域的出現或消失，不同吸引域之間相互侵蝕導致安全-吸引盆侵蝕。下文借助多初值分岔圖和TLE圖進一步分析安全-吸引盆侵蝕與分岔過程。

沿用上文所選系統參數，計算得到系統的多初值分岔圖和TLE圖，分別如圖9和圖10所示。為分析多初值下系統的穩態響應及其轉遷過程，多初值分岔圖中采用時間Poincaré截面(每隔一個外激勵周期2π/ω取Poincaré映射點)。圖9中分岔分支的顏色對應于圖7中的安全-吸引盆顏色；P1、M2、PN、MN等為運動類型；PN和MN為混沌運動。圖9和圖10中G12、M12和D12等為分岔點或周期跳躍點，部分倍化序列未標注。

圖9中橙色分岔分支：P1→D12→P2→G22。當Fm∈(0.185 8,0.35)時，安全-吸引盆中橙色P1S區域為安全吸引子P1的吸引區域(圖7(a)～(d))。當Fm=0.185 8(D12)時，圖10中TLE值近似等于0，橙色分岔分支發生倍化分岔，安全吸引子P1倍化分岔為安全吸引子P2；Fm∈(0.164 4,0.185 8]時，橙色P2S區域為P2吸引子的吸引區域(圖7(e)～(g))。當Fm=0.164 4時，P2吸引子及橙色區域消失(圖7h)。

圖9中藍色分岔分支：P1→G12→P2→G24→ P4→G4N→MN。當Fm=0.290 3(G12)時，安全-吸引盆中出現不安全吸引子P21，部分橙色區域進入P21吸引子的吸引區域，當Fm∈(0.153 9,0.290 3]時，藍色區域為P21吸引子的吸引區域(圖7(b)～(i))。當Fm=0.153 9(G24)時，藍色區域P21不安全吸引子倍化分岔為安全吸引子P4，Fm∈(0.143 5,0.153 9]時，藍色區域為P4吸引子的吸引區域(圖7(j))。當Fm=0.143 5(G4N)時，安全吸引子P4分岔為安全吸引子PN，當Fm∈(0.1,0.143 5]時，藍色區域為PN吸引子的吸引區域(圖7(k))。

圖9中紅色分岔分支：P1→M12→M2。當Fm=0.269 9(M12)時，安全-吸引盆中出現不安全吸引子P22，部分橙色區域進入P22吸引子的吸引區域；當Fm∈(0.1,0.269 9]時，紅色區域為P22吸引子的吸引區域(圖7(c)～(k))。

圖9中紫色分岔分支：P1→G12→P2→G26→P6→G6-12→G12N→PN→GN2。當Fm=0.178(G26)時，安全-吸引盆中出現不安全吸引子P6，藍色部分區域進入P6吸引子的吸引區域，當Fm∈(0.161 2,0.178]時，紫色區域為P6吸引子的吸引區域，(圖7(f)～(h))。當Fm=0.161 2(G6-12)時P6吸引子變為P12吸引子，并在之后進入短暫的混沌狀態。當Fm=0.158 7時，安全-吸引盆中紫色區域完全被侵蝕。Fm∈(0.153 9,0.158 7]時，安全-吸引盆中只存在P21和P22吸引區域(圖7(i))。

圖9 隨Fm減小的多初值分岔圖

圖10 隨Fm減小的TLEFig.10 TLE decreased with Fm

圖9中黃銅色分岔分支：P1→G12→P2→G23 →P6→G6N→PN→PN2。當Fm=0.173 7(G6N)時，部分紫色區域進入不安吸引子PN的吸引區域，當Fm∈(0.165,0.173 7]時，黃銅色區域為不安全吸引子PN的吸引區域(圖7(g))。當Fm=0.165時，黃銅色吸引域消失。

由此可見，隨著Fm的減小，系統的多初值分岔圖和安全-吸引盆侵蝕與分岔過程相對應。多初值分岔圖中未出現周期跳躍和分岔時，不會引起安全-吸引盆中吸引子種類和數量上的改變，安全-吸引盆發生侵蝕。多初值分岔圖中出現周期跳躍或分岔，安全-吸引盆中吸引子種類或數量改變，安全-吸引盆發生分岔。

3.2 參數D變化下安全-吸引盆侵蝕與分岔

取系統參數ω=1.2，ε=0.2，ξ=0.07，k=0.18，Fm=0.14，μ=0.05。在系統相空間中選擇考察區域H2∈{-2≤x1≤2,-2≤x2≤-2}。圖11為D∈(0,1.0)內增大時系統的安全-吸引盆。圖12為以新出現或數量變化的吸引子為初值計算得到的σFi(t)。

表3中列出了當D∈(0,1.0)時系統安全-吸引盆中吸引子的共存情況和演變過程。當D∈(0,0.085 5)時，安全-吸引盆中只存在安全吸引子P1，圖11(a)為D=0.05時系統的安全-吸引盆，圖中紫色區域為該吸引子的吸引區域。以P1吸引子x1=-0.191 429、x2=0.048 571為初值計算得到圖12(a)，可以判斷紫色區域為安全區域，將其標為P1S。

表3 系統吸引子隨D減小的演變過程

當D增大至D=0.085 5時，安全-吸引盆中出現不安全吸引子P41，P1S紫色區域中部分初值進入P41吸引子的吸引區域。當D∈[0.085 5,0.103)時，安全-吸引盆中P1和P41吸引子共存。圖11(b)為D=0.09時的安全-吸引盆，圖中粉色區域為P41吸引子的吸引區域，以P41吸引子x1=-0.534 286,x2=-0.054 286為初值計算得圖12(b)，粉色區域為不安全區域，記為P4U。圖11(c)為D=0.1時的安全-吸引盆，其中的紫色區域增大，粉色區域減小；吸引子的類型和數量未發生變化，安全-吸引盆僅發生了侵蝕。

當D=0.103時，粉色區域及其P41吸引子消失。當D=0.109 5時，安全-吸引盆中出現安全吸引子P3。當D∈[0.109 5,0.122 5)時，安全-吸引盆中P1和P3共存。圖11(d)為D=0.115時的安全-吸引盆，圖中草綠色區域為P3吸引子的吸引區域，以P3吸引子x1=-0.237 143,x2=-0.048 571為初值計算得到圖12(c)，綠色區域為安全區域，記為P3S。

當D=0.122 5時，紫色區域中P1吸引子分岔為安全吸引子P21；當D∈[0.122 5,0.253 5)時，安全-吸引盆中P21和P3共存。圖11(e)為D=0.175時的安全-吸引盆，以紫色區域P21吸引子x1=-0.237 143,x2=0.031 429為初值計算得到圖12(d)，紫色區域安全，記為P2S。D∈[0.122 5,0.253 5)時，紫色區域不斷侵蝕草綠色區域(圖11(e)～(f))。當D=0.253 5時，草綠色區域及其P3吸引子消失。

當D=0.386 5時，安全-吸引盆中出現安全吸引子P22，P2S紫色區域中部分初值進入P22吸引子的吸引區域。當D∈[0.386 5,0.433 5)時，安全-吸引盆中P21和P22共存。圖11(g)為D=0.41時的安全-吸引盆，圖中天藍色區域為P22吸引子的吸引區域，以P22吸引子x1=-0.46,x2=-0.02為初值計算得到圖12(e)，天藍色區域為安全區域，記為P2S2。

當D=0.433 5時，天藍色區域中P22吸引子分岔為安全吸引子P4。當D∈[0.433 5,0.457 5)時，安全-吸引盆中P21和P4共存。圖11(h)為D=0.45時的安全-吸引盆，以天藍色區域P4吸引子x1=-0.597 143,x2=-0.042 857為初值計算得到圖12(f)，天藍色區域為安全區域，記為P4S。當D=0.457 5時，天藍色區域及其P4吸引子消失。

當D=0.525 5時，安全-吸引盆中出現不安全吸引子P42，P2S紫色部區域中部分初值進入P42吸引子的吸引區域。當D∈[0.525 5,0.582)時，安全-吸引盆中P21和P42共存。圖11(i)為D=0.55時的安全-吸引盆，圖中紅色區域為P42吸引子的吸引區域，以P42吸引子x1=-0.62,x2=-0.06為初值計算得到圖12(g)，紅色區域為不安全區域，記為P4U2。

當D=0.582時，安全-吸引盆中出現不安全吸引子P43；當D=0.589時，紅色區域不安全吸引子P42分岔為不安全吸引子P2。當D∈[0.589,0.74)時，安全盆中P21、P2和P43共存；圖11(k)為D=0.625時的安全-吸引盆，其中的藍色區域為P43吸引子的吸引區域。以P43吸引子x1=0.094 286,x2=-0.265 714為初值計算得到圖12(h)，藍色區域為不安全區域，記為P4U3。以紅色區域P2吸引子x1=-0.905 714,x2=-0.128 571為初值計算得到圖12(i)，紅色區域為不安全區域，記為P2U。

當D=0.74時，安全-吸引盆中出現不安全吸引子P6，P4U3藍色區域中部分初值進入P6吸引子的吸引區域。當D∈[0.74,0.878)時，安全-吸引盆中P21、P2、P43和P6共存。圖11(m)為D=0.75時的安全-吸引盆，其中的春天綠區域為該吸引子吸引區域，以P6吸引子x1=-0.322 857,x2=0.42為初值計算得到圖12(j)，春天綠區域為不安全區域，記標為P6U。圖11(n)為D=0.75時的安全-吸引盆。

當D=0.878時，不安全吸引子P2及紅色區域消失。當D∈[0.878,1.0)時，安全-吸引盆中P21、P43和P6共存，圖11(o)為D=0.9時系統的安全-吸引盆。

(a) D=0.05(b) D=0.09

(c) D=0.1(d) D=0.115

(e) D=0.175(f) D=0.225

(g) D=0.41(h) D=0.45

(i) D=0.55(j) D=0.575

(k) D=0.625(l) D=0.7

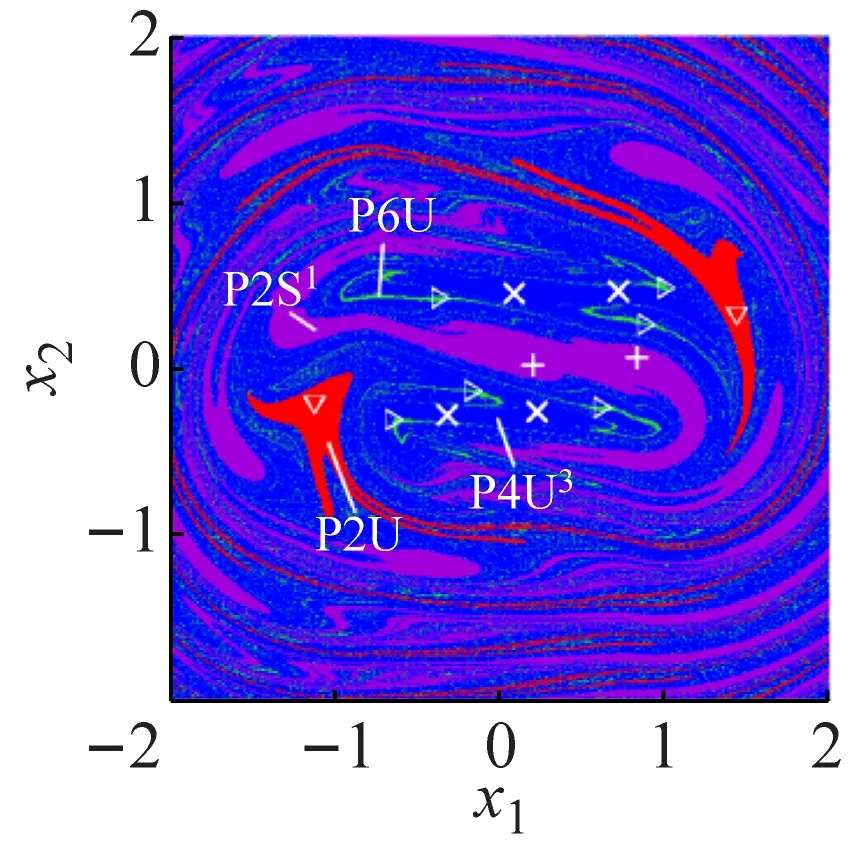
(m) D=0.75(n) D=0.8

(o) D=0.9圖11 系統安全-吸引盆隨D的侵蝕與分岔過程Fig.11 Erosion and bifurcation of safe basins of system via D

由此可見，隨著齒側間隙D的增大，系統安全-吸引盆中出現多吸引域共存和不安全吸引域，且不安全吸引域的面積不斷增大，系統的穩定性和安全特性被破壞。因此，齒側間隙D不宜取值過大。

下文將利用多初值分岔圖和TLE圖分析系統安全-吸引盆的侵蝕與分岔過程。圖13為D∈(0,1.0)內系統隨D增大的多初值分岔圖，圖14為對應的TLE圖。

圖13中紫色分岔分支：P1→G12→P2。當D∈(0,0.122 5)時，安全-吸引盆中紫色區域為安全吸引子P1吸引區域(圖11(a)～(d))。當D=0.122 5(G12)時，P1吸引子分岔為安全吸引子P21。D∈[0.122 5,1)時，安全-吸引盆中紫色區域為P21吸引子的吸引區域(圖11(e)～(o))。

圖13中粉色分岔分支：P1→G14→P4→G41。當D=0.085 5(G14)時，安全-吸引盆中出現不安全吸引子P41，當D∈(0.085 5,0.103)時，安全-吸引盆中粉色區域為P41吸引子的吸引區域(圖11(b)～(c))。當D=0.103(G41)時，粉色區域及其P41吸引子消失。

圖13中草綠色分岔分支：P1→G13→P3 →G32。當D=0.109 5(G13)時，安全-吸引盆中出現安全吸引子P3；當D∈[0.109 5,0.253 5)時，安全-吸引盆中草綠色區域為P3吸引子的吸引區域(圖11(d)～(f))。當D=0.253 5(G32)時，草綠色區域及其P3吸引子消失。

(a) D=0.05(b) D=0.09

(c) D=0.115(d) D=0.175

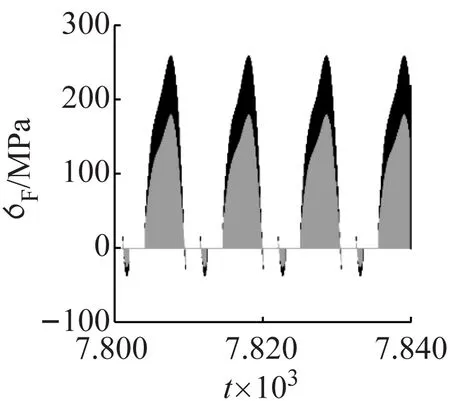
(e) D=0.41(f) D=0.45

(g) D=0.55(h) D=0.625(P4U3)

(i) D=0.625(P2U)(j) D=0.75圖12 隨t變化的σF1和σF2Fig.12 σF1 and σF2 via t

圖13中天藍色分岔分支：P1→G12→P2→G22→P2→G24→P4→G42。當D=0.386 5(G22)時，安全-吸引盆中出現安全吸引子P22，當D∈[0.386 5,0.433 5)時，安全-吸引盆中天藍色區域為P22吸引子的吸引區域(圖11(g))。當D=0.433 5(G24)時，安全吸引子P22倍化分岔為安全吸引子P4。當D∈[0.433 5,0.457 5)時，安全-吸引盆中天藍色區域為P4吸引子的吸引區域(圖11(h))。當D=0.457 5(G42)時，天藍色區域及其P4吸引子消失。

圖13中紅色分岔分支：P1→G12→P2→M24→Q4→M42→P2→O24。當D=0.525 5(M24)時，安全-吸引盆中出現不安全吸引子P42，當D∈[0.525 5,0.589)時，安全-吸引盆中紅色區域為P42吸引子的吸引區域(圖11(i)～(j))。當D=0.589時，紅色區域P42吸引子逆倍化分岔為不安全吸引子P2，當D∈[0.589,0.878)時，安全-吸引盆中紅色區域為P2吸引子的吸引區域(圖11(k)～(n))。

圖13 隨D增大的多初值分岔圖

圖14 隨D增大的TLEFig.14 TLE increased with D

圖13中藍色分岔分支:P1→G12→P2→M24→Q4→G44→R4。當D=0.582時，安全-吸引盆中出現不安全吸引子P43，當D∈[0.582,1.0)時，安全-吸引盆中藍色區域為P43的吸引區域(圖11(k)～(o))。

圖13中春天綠色分岔分支：P1→G12→P2→M24→Q4→G44→R4→G46→P6。當D=0.74時，安全-吸引盆中出現不安全吸引子P6，當D∈[0.74,1.0)時，安全-吸引盆中春天綠色區域為P6吸引子的吸引區域(圖11(m)～(o))。

由此可見，多初值分岔圖中系統隨D增大的分岔過程，反應了系統運動響應的共存情況及其轉遷過程。這些運動響應的出現、消失或轉遷，引起安全-吸引盆中吸引子的出現或消失，發生安全-吸引盆分岔。若運動響應的共存情況未發生改變，安全-吸引盆中不同吸引域之間僅出現相互侵蝕。

4 結 論

本文建立了齒輪傳動系統的齒根安全條件，結合吸引子判斷吸引盆中不同運動類型吸引域的安全特性，獲得了系統的安全-吸引盆。研究了單自由度多狀態嚙合齒輪傳動系統在負載Fm和齒側間隙D變化下安全-吸引盆的侵蝕與分岔過程。

(1) 隨著負載Fm的減小，安全-吸引盆中出現吸引子共存。部分吸引域下的系統響應不滿足齒根安全條件，不安全吸引域的吸引域面積增大導致安全-吸引盆中不安全區域增大。參數Fm和吸引域的演變共同影響系統的穩定性和安全特性。

(2) 隨著齒側間隙D的增大，安全-吸引盆中安全區域減小，不安全區域的面積增大，系統的安全性逐漸變差。參數D過大會加劇輪齒碰撞等現象，在設計時，D值不應過大。

(3) 吸引子的種類或數量變化導致安全-吸引盆中的運動拓撲結構改變，安全-吸引盆發生分岔。多初值分岔圖中出現周期跳躍或分岔引起系統穩態響應的變化，導致安全-吸引盆中吸引子發生變化，誘發安全-吸引盆分岔。

本文根據系統穩態響應下齒根彎曲應力是否超過齒根許用彎曲應力考察齒輪傳動系統安全-吸引盆的分岔與侵蝕過程貼近工程實際。本文只建立了防止輪齒折斷的安全條件，下一步將建立防止齒面點蝕、齒面塑性變形等安全條件并分析系統安全-吸引盆的侵蝕與分岔過程。