輸電線路導線陣風響應系數研究

楊風利，張宏杰，王 飛，黃 國

(中國電力科學研究院有限公司，北京 100055)

準確計算導線風荷載是輸電線路桿塔結構抗風設計和防風偏設計的基礎，而考慮自然風空間尺度影響的導線陣風響應系數是導線風荷載計算的重要參數之一。自然界風場中湍流普遍存在，大尺度空間結構所受風荷載不能用一點風速表征，而應進行適當折減。導線風場不均勻特征和風振響應特性共同影響其風荷載大小，現行各國(組織)通過單一系數或組合系數兩種方式來考慮兩者的共同影響。美國ASCE規范[1]、歐洲標準[2]等采用導線陣風響應系數綜合表征導線風場不均勻特征和風振響應特性，該系數物理意義較為明確，且綜合考慮了檔距、風速及地貌類型、湍流積分尺度等因素影響。日本[3]和德國[4]規范采用風壓不均勻系數(又稱“構造規模折減系數”)來考慮結構脈動風荷載非均勻性對結構風致響應的折減，其計算公式是由實測數據擬合得到的。GB 50545—2010[5]采用導線風壓不均勻系數α和風荷載調整系數βc的乘積來表征導線陣風荷載特性，風壓不均勻系數α計算公式的兩項常系數均取日本和德國規范的較大值；結合輸電線路運行經驗，規定計算桿塔風荷載時，不同風速下導線風荷載調整系數βc在1.0～1.3取值；總的來說，GB 50545—2010方法缺乏理論基礎，且僅與導線檔距和風速有關，未考慮地貌類型和湍流積分尺度的影響。2019年頒布實施的DL/T 5551—2018規范[6]給出了導線陣風系數和檔距折減系數的計算方法，兩個參數的乘積與ASCE規范陣風響應系數相當，只是具體計算方法略有差異。

目前，針對導線陣風響應系數或風壓不均勻系數的研究手段包括理論分析和現場實測兩類。在理論分析方面，陣風荷載因子法(GLF)是結構等效靜力風荷載計算的經典方法，最早由Davenport[7]于20世紀60年代提出，Davenport[8-9]基于GLF方法推導了塔線體系風振響應的計算表達式，通過近似解耦方法分別得到了導線和輸電鐵塔陣風響應系數的計算公式，同時給出了考慮地貌類型影響的導線檔距系數，這些理論被美國ASCE規范采用并沿用至今，后續其他學者[10-17]關于導線陣風響應的理論研究大都是基于GLF方法開展的。Loredo-Souza等[18-19]將背景響應分量中的振型函數用影響線函數替代，發展了統計影響線法，但ASCE為保持規范的延續性，仍然延用了按原GLF方法推導的公式。現有的導線陣風荷載分析理論中，大都根據地貌類型假定湍流積分尺度為一定值，忽略了其隨高度的變化特性。

在現場實測研究方面，樓文娟等[20]通過時長2 616 h、水平尺度涵蓋100 m范圍的風場實測資料，建立了湍流尺度的空間范圍內的水平相關函數模型，構建了風場相關函數表達式，并與現有的相關函數模型進行了對比。張宏杰等[21]研制了6點位脈動超聲風和懸垂串風偏傾角同步觀測系統，采集了空間同步風速數據和風偏傾角數據，分別參照Davenport空間相關性分析理論和合力比值法，提出了同時考慮平均風和脈動風不均勻性的風壓不均勻系數計算公式。卞榮等[22]在丘陵地區輸電線路沿線構建了一套多點同步風速監測系統，基于現場實測數據分析了丘陵地形周邊的水平風場特性，計算了不同檔距條件下的平均風速不均勻系數和極值風速不均勻系數，但測試系統只包含3個超聲風速儀且間距超過100 m，超過了湍流積分尺度，一定程度上限制了其研究結果的精確程度。20世紀90年代，美國電力科學研究院輸電線路力學研究中心(TLMRC)[23]通過實測研究了風速峰值因子、構件荷載響應系數和導線陣風響應系數，并給出了詳細的觀測流程及數據處理方法。目前已開展的實測研究存在實測檔距小(一般在100～200 m)或測點間隔大的缺點，不能完全滿足大檔距導線陣風荷載精確計算的要求，但實測結果可以作為理論分析研究的有益補充。

上述理論和實測研究為完善導線風荷載及陣風響應計算理論提供了重要參考和依據，但導線陣風響應系數計算時，影響因素眾多，大都對共振響應分量、湍流積分尺度和分離系數等參數進行了簡化或近似，其對導線陣風響應的影響規律還不明確，需要開展進一步的研究。

針對以上問題，本文以陣風荷載因子法(GLF)為基礎，推導了不同檔數、影響線函數下導線陣風響應系數的計算公式，研究了湍流積分尺度、檔距、風速、共振響應分量、分離系數和峰值因子等因素對導線陣風響應系數的影響規律，并將其與美國ASCE規范和中國規范的導線陣風響應系數進行了比較分析，提出了現行規范導線陣風響應系數計算方法的改進建議。

1 導線陣風響應系數基本計算理論

1.1 基本計算理論

與豎向風剖面類似，在沿導線順線路的水平方向上，任意兩點的水平風速不是完全相同的，可以采用圖1所示的曲線剖面來描述。

圖1 水平方向風剖面Fig.1 Horizontal wind profile

風荷載作用下的輸電線路塔線體系如圖2所示，坐標原點位于中間1基桿塔的導線掛點上，x方向為順線路方向坐標軸，兩側導線檔距分別為L1和L2，水平檔距Lp=(L1+L2)/2，s為導線弧垂，導線平均高度z為導線形心至地面的距離。具體來講，檔距為導線兩個懸掛點之間的水平距離，弧垂為導線最低點與兩懸掛點間連線的垂直距離。

圖2 輸電線路塔線體系定義Fig.2 Definition of the transmission tower-line system

(1)

當忽略共振響應分量時，導線陣風響應的表達式為

Gw=1+2gIzJ(x)

(2)

式中：Iz為導線平均高度z處的湍流強度；J(x)為導線風致振動背景響應分量的聯合接納函數。

導線風致振動背景響應分量的聯合接納函數平方項J2(x)的表達式如下

(3)

式中：Ld、Lu分別為導線檔距方向的積分上限和積分下限；x、x′為沿導線檔距方向的坐標；Ls為湍流積分尺度；i(x)、i(x′)為影響線函數。

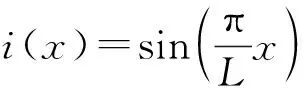
(4)

假定桿塔兩側導線檔距L1=L2=L，采用MATLAB對式(3)進行符號積分，分別計算得到與兩種影響線函數和檔數對應的聯合接納函數J2(n)表達式。Ld=0、Lu=L、i(x)=x/L時，J2(n)的表達式見式(4)，其余3種情況的J2(n)表達式如下

(5)

(6)

(7)

1.2 現行規范計算方法

(1) 美國ASCE規范導線陣風響應系數Gw的計算方法如下

(8)

式中：峰值因子g取值范圍為3.5～4.0，推薦取值為3.6；ε為導線風振響應與輸電鐵塔風振響應平方項分離的近似系數，ε=0.75；Bw為導線無量綱背景響應分量；Rw為導線無量綱共振響應分量，ASCE規范認為其對導線陣風響應的影響可以忽略；E為導線平均高度z處的暴露系數，E=2Iz；Kv為3 s陣風風速與10 min平均風速的比值，對應的設計風速時距為3 s。

導線無量綱背景響應分量Bw的計算式為

(9)

(2) 中國DL/T 5551—2018《架空輸電線路荷載規范》給出了導線風荷載計算方法，其中導線陣風系數βc與檔距折減系數αL的乘積同ASCE規范的陣風響應系數Gw相當，即

Gw=βcαL=γc(1+2gεcIzδL)

(10)

式中：γc為導線風荷載折減系數，用于考慮最不利風向的折減，取0.9；峰值因子g取2.5；εc為導線風荷載脈動折減系數，其含義與ASCE規范中的分離系數ε類似，用于考慮結構敏感性與塔線疊加相關性，但其取值結合了中國輸電線路行業多年來的設計和運行經驗；δL為檔距相關性積分因子。

檔距相關性積分因子δL是關于水平檔距Lp和湍流積分尺度Ls的函數，計算表達式為

(11)

結合1.1節導線風振響應隨機振動理論推導過程，根據ASCE規范和DL/T 5551—2018關于導線陣風響應系數Gw的相關規定，可以得到背景響應分量、檔距相關性積分因子和聯合接納函數存在如下關系

(12)

2 參數影響分析

2.1 影響線函數和檔數對聯合接納函數的影響

式(12)所列各項是計算導線陣風響應系數Gw的關鍵參數，后面統稱“聯合接納函數”。影響其數值的參數較多，下面分析湍流積分尺度按ASCE規范三類地貌取值，影響線函數和檔數對聯合接納函數的影響規律。

圖3給出了變化湍流積分尺度Ls、影響線函數i(x)和導線檔數等參數時，聯合接納函數J2(n)的變化曲線及與ASCE規范背景響應分量系數Bw的對比情況。

由圖3(b)可以看出，僅考慮一檔導線風場相關性，影響線函數分別為線性函數和正弦函數時，聯合接納函數J2(n)的數值非常接近，即影響線函數類型對聯合接納函數J2(n)的影響可以忽略。

由圖3(c)可以看出，與僅考慮單檔導線的風場不完全相關性相比，考慮兩檔導線風場不完全相關性計算得到的聯合接納函數J2(n)較小；檔距L>260 m時，兩檔聯合接納函數J2(n)比單檔計算值小50%以上。

(a) 湍流積分尺度Ls(b) 影響線函數(c) 檔數

2.2 風速、檔距對陣風響應系數的影響

以美國ASCE規范附錄F中的算例進行變參數分析。已知導線型號為LGJ 630/45，導線外徑d=33.6 mm，導線平均高度z=24.4 m，C類場地(與中國B類相當)，湍流積分尺度Ls=67.1 m，風剖面冪指數αFM=7，梯度高度zg=274.5 m，表面阻力系數κ=0.005。后續2.3節～2.5節分析采用的導線等參數與2.2節相同。

3 s設計風速v=28.6 m/s、35.75 m/s、42.9 m/s和50.05 m/s的情況下，對100～1 000 m檔距的導線陣風響應系數Gw進行了計算，不同檔距導線陣風響應系數隨風速的變化曲線如圖4所示。由圖4可以看出，在檔距一定的條件下，隨風速v增加，導線陣風響應系數Gw略有增大，增大幅度不超過2.1%。與風速相比，檔距對導線陣風響應的影響更為顯著，隨著檔距差的增加，陣風響應系數最大降低25.9%。

2.3 湍流積分尺度對陣風響應系數的影響

美國ASCE規范沿用了Davenport理論，在未對湍流積分尺度Ls進行實測的情況下，B類場地統一取為67.1 m，這忽略了導線平均高度z對湍流積分尺度Ls的影響，也是實測導線陣風響應系數Gw與ASCE規范取值差異較大的原因。為此，參考JTG/T 3360-01—2018《公路橋梁抗風設計規范》[24]，不同導線平均高度z對應的湍流積分尺度Ls見表1，湍流積分尺度隨導線平均高度的增加而增大。

圖4 不同風速下Gw隨檔距L的變化曲線Fig.4 Gw variation with the conductor span L and wind speed v

在3 s陣風設計風速v=42.9 m/s(10 min平均風速為30 m/s)風速下，對100～1 000 m檔距的導線陣風響應系數進行了計算，不同湍流積分尺度Ls下導線陣風響應系數Gw隨檔距L的變化曲線如圖5所示。由圖5可知，檔距一定時，隨著導線平均高度z增加，湍流積分尺度Ls不斷增大，導線陣風響應系數Gw略有增大，增大幅度不超過8.4%。與湍流積分尺度相比，檔距L對導線陣風響應系數的影響更為顯著，陣風響應系數Gw隨檔距的增加而減小，不同湍流積分尺度下Gw隨Ls的變化趨勢基本一致，最大降低幅度為21.9%～23.9%。綜合2.2節分析結果，檔距由100 m增至1 000 m時，陣風響應系數至少降低20%以上。

表1 湍流積分尺度隨導線平均高度的變化

圖5 不同湍流積分尺度的Gw曲線Fig.5 Gw variation with the turbulence scale Ls

2.4 共振響應分量對陣風響應系數影響

美國ASCE規范給出的導線陣風響應系數Gw完全表達式見式(8)。該規范附錄F4中認為，導線和輸電鐵塔的共振響應分量Rw、Rt對塔線體系風振響應的貢獻可以忽略。這種假設的根據為，一是實際未觀測到輸電線路的塔線耦合共振現象，二是導地線、輸電鐵塔的峰值振動響應不可能同時出現。此外，導地線的氣動阻尼會顯著削弱它們的共振響應，因而擬靜力背景響應是起主導作用的響應成分。下面按照美國ASCE規范的計算方法，定量評估導線共振響應分量Rw對陣風響應系數Gw的影響程度，本文共振響應分量Rw采用了美國ASCE規范的計算公式。

3 s陣風設計風速v=10～56 m/s時，圖6(a)給出了考慮共振響應分量Rw前后導線陣風響應系數Gw的變化曲線。可以看出，考慮共振響應分量Rw影響后，不同設計風速對應的陣風響應系數Gw增大2.2%～6.4%，Rw隨設計風速v的增大逐漸增大，其對Gw影響程度也隨之增大。

檔距L=100～1 000 m(弧垂s=1～60 m)時，圖6(b)給出了考慮共振響應分量Rw前后導線陣風響應系數Gw的變化曲線。可以看出，考慮共振響應分量Rw影響后，不同檔距導線的陣風響應系數Gw增大5.3%～6.9%，但Rw的影響程度與導線檔距L關系不大。

綜合上述分析，忽略導線共振響應分量Rw影響，導致導線陣風響應系數Gw計算值即導線設計風荷載偏小5%以上。

(a) 設計風速v

(b) 檔距L圖6 Gw隨共振響應分量Rw的變化曲線

2.5 分離系數和峰值因子對陣風響應系數的影響

假定輸電線路塔線體系導線脈動風風振響應和輸電鐵塔脈動風風振響應之比的取值范圍為1～10，分離系數ε取值范圍為0.71～0.91。按照美國ASCE規范計算導線陣風響應系數Gw，檔距L=381.25 m，弧垂s=10 m，計算得到的陣風響應系數Gw曲線見圖7。可以看出，導線陣風響應系數Gw隨分離系數ε的增大而線性增加，ε=0.91對應的Gw比ε=0.75對應的Gw增大約5.5%。

圖7 Gw隨分離系數ε變化曲線Fig.7 Gw variation with the response separation coefficient ε

美國ASCE規范中峰值因子g取3.5～4.0(典型取值為3.6)，而DL/T 5551—2018中峰值因子g=2.5，兩者取值差異較大。Davenport按照首次穿越理論提出的峰值因子計算表達式為[25]

(13)

式中：n1為導線的一階自振頻率；T為脈動風時距，即導線風振響應取得最大值的時間間隔，一般取600 s。

按照式(13)可以計算得到檔距100～1 000 m導線的峰值因子，導線一階自振頻率n1和峰值因子g隨導線檔距的變化曲線如圖8所示。隨檔距增大，導線一階自振頻率和峰值因子逐漸降低，峰值因子的變化范圍為2.95～3.58。

圖8 一階自振頻率n1和峰值因子g的變化曲線

下面分析峰值因子g在2～4取值時導線陣風響應系數Gw的變化規律，其變化曲線見圖9。可以看出，按照美國ASCE規范g=3.6比按照中國DL/T 5551—2018中g=2.5計算得到的陣風響應系數Gw高8.6%。

圖9 Gw隨峰值因子g的變化曲線Fig.9 Gw variation with the peak factor g

3 與現行規范的對比分析

B類場地、Ls=67.1 m時，單檔和連續兩檔、線性與正弦曲線影響線函數下的聯合接納函數曲線與ASCE規范的對比如圖10所示。由圖10可以看出，按單檔導線計算的聯合接納函數J2(n)明顯小于美國ASCE的Bw；按連續兩檔導線、影響線為正弦函數計算的聯合接納函數J2(n)與美國ASCE規范的Bw基本一致，最大相差不超過6%；影響線為線性函數計算的聯合接納函數J2(n)略高于美國ASCE規范的Bw，檔距L=180 m時最大相差約24.4%，即按照兩檔線性函數計算導線陣風響應系數偏于安全。

圖10 與規范曲線對比分析Fig.10 Comparison with the standard curves

當僅計算單檔導線跨中最大風致位移時，顯然應該只考慮單檔導線上的風場不完全相關性，即按式(4)或式(5)計算聯合接納函數J2(n)，否則會導致結果偏于不安全。當計算導線上風荷載導致的輸電塔風致響應(力或位移)時，應考慮輸電塔兩側共兩檔導線上的風場不完全相關性。而在式(6)或式(7)兩種計算方法里，盡管式(7)和美國ASCE規范Bw值非常接近，但采用線性影響線函數即按照式(6)更為合理，式(6)與中國DL/T 5551—2018規范中δL的平方是完全一致的。

4 結 論

本文推導了單檔和連續兩檔、影響線函數為線性函數和正弦函數的輸電線路導線陣風響應系數計算公式，不考慮各參數間的耦合影響，分別研究了湍流積分尺度、檔距、風速、共振響應分量、分離系數和峰值因子等因素對導線陣風響應系數的影響規律，并將其與現行規范進行了比較分析，得到的主要結論如下：

(1) 計算導線跨中位移和輸電塔風致響應時，應分別考慮單檔和相鄰兩檔導線上的風場不完全相關性。影響線函數采用線性函數或正弦函數時，其差異對導線陣風響應的影響可以忽略。

(2) 檔距一定時，隨風速增大，陣風響應系數略有增大，增大幅度不超過2.1%；隨導線平均高度增加，湍流積分尺度不斷增大，陣風響應系數略有增大，增大幅度不超過8.4%；與風速和湍流積分尺度相比，檔距對陣風響應系數的影響更為顯著，檔距從100 m增至1 000 m，陣風響應系數至少降低20%。

(3) 忽略導線共振響應分量Rw影響，導線陣風響應系數Gw計算值即導線設計風荷載會偏小5%以上，建議設計時予以考慮。

(4) 峰值因子對導線陣風響應系數的影響較為顯著，峰值因子g按照ASCE規范取3.6比按照DL/T 5551—2018規范取2.5計算得到的陣風響應系數Gw高8.6%。精細化計算導線陣風荷載時，需要根據導線自振頻率和脈動風時距計算確定。