航空電子模塊儲熱器工作時間預測

吳 波，張豐華，田 灃，醋強一

（中國航空工業集團有限公司西安航空計算技術研究所，陜西西安710068）

航空電子模塊是戰斗機、空空導彈等航空飛行器中實現信息測量、采集、傳輸、處理、監控及顯示功能的基本載體。新一代戰斗機、空空導彈等的性能更加強大［1-2］，其航空電子模塊的功能越來越復雜，總功耗也越來越大。而“小、低、輕”是對航空電子模塊的必然要求，這使得航空電子模塊的熱管理問題越來越突出：一方面飛行器的性能增強導致功耗增大；另一方面其自身的空間尺寸和質量受到嚴格的限制。因此，通過引入外部工質實施對流冷卻的方案在很多情況下并不可行，例如遠端安裝的航空電子模塊不便于流體管路的布置。相變儲熱器是一類依靠相變材料吸熱熔化來儲存熱量的裝置，可與航空電子模塊集成在一起，以便實施熱管理［3］。當航空電子模塊具有短時工作特點時，相變儲熱器更能發揮作用。

工程師在設計儲熱器時需要關注的核心問題是：根據熱源芯片的許用溫度和功耗來判斷儲熱器從航空電子模塊開始加電運行到熱源芯片達到許用溫度的時間，即儲熱器的工作時間。采用數值傳熱學方法及CFD（computational fluid dynamics，計算流體動力學）軟件可以對儲熱器的工作時間進行數值仿真計算。但是，相變傳熱過程的精確數值模擬較為復雜，不適合應用于需要迅速響應的工程設計中，也不便在非傳熱學背景的結構設計工程師中推廣。因此，為了滿足工程設計中對設計工具的“易用”“速用”需求，筆者擬構建儲熱器工作時間與功耗、設定溫度的數學關系式。

目前，已有大量關于類似相變儲熱器結構的基礎研究和應用研究［4-10］，其可為本文的研究提供重要參考。但是，這些研究未綜合考慮航空電子模塊儲熱器實際工作時與自然對流和熱輻射的耦合作用，也缺乏在航空電子模塊熱管理工程背景下對儲熱器工作時間的預測。

基于此，筆者擬開展以下工作。首先，綜合考慮航空電子模塊儲熱器在實際工作時其頂面的自然對流和熱輻射，運用傳熱學理論構建儲熱器熱模型。然后，運用焓-多孔介質法對儲熱器進行數值模擬，并以頂面絕熱條件下的儲熱器為參照，分析儲熱器在工作過程中的溫升規律及其相變材料的熔化進程。接著，根據已有的相變儲熱器研究結果，結合數值模擬結果，分析儲熱器工作時間與功耗、設定溫度之間的依變關系。最后，運用二元線性回歸方法擬合得到儲熱器工作時間的預測公式，并通過獨立的數值模擬數據集來驗證該預測公式的準確性。

1 航空電子模塊儲熱器熱模型

航空電子模塊儲熱器是通過焊接密封的方式將固-液相變材料封裝在金屬腔體內部的。金屬腔體內部有1組等間距的肋片，用于增強腔體內部的換熱。如圖1所示，航空電子模塊由印制電路板（printed circuit board，PCB）和電子芯片組成，并通過緊固件與儲熱器連接。電子芯片工作時產生的熱量通過熱傳導的方式傳輸給儲熱器，儲熱器內部的相變材料吸收熱量。當相變材料達到熔點時，其溫度幾乎保持不變，從而實現對電子芯片的溫度控制。儲熱器內部每2個肋片對稱面之間的部分為儲熱器的最小單元，即圖1 中虛線框內部分。假設電子芯片的熱量均勻地分布在儲熱器底面上，則該最小單元可視作表征儲熱器儲熱過程的特征單元體，通過研究該特征單元體工作時間的特性，即可得到整個儲熱器工作時間的特性。儲熱器單元體的幾何模型如圖1下方所示，其幾何尺寸如表1所示，其中L為儲熱器的總長度，a和b分別為儲熱器單元體左、右側和上、下側金屬壁的厚度，H和l 分別為儲熱器單元體金屬腔體的高度和寬度。儲熱器單元體金屬壁面的材料為鋁6061，內部相變材料為RT80，其熱物性參數詳見文獻［11］。

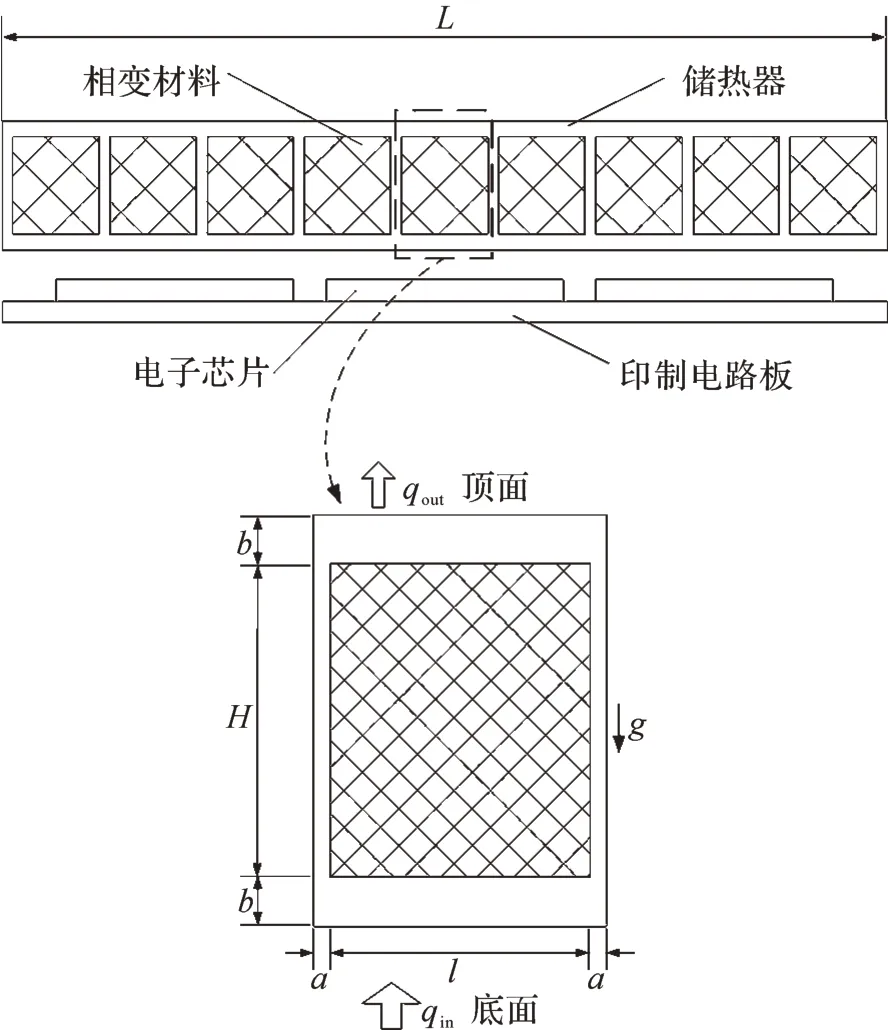
圖1 航空電子模塊儲熱器熱模型Fig.1 Thermal model of heat storage device in avionics module

表1 儲熱器幾何尺寸Table 1 Geometric dimensions of heat storage device

儲熱器單元體的底面接收由電子芯片產生的均勻、熱流密度恒定的熱量，頂面直接暴露在外部環境中，通過自然對流和熱輻射向環境散熱，兩者的熱量差以相變材料潛熱的形式儲存在儲熱器中。假設儲熱器的總長度和總寬度均為L，則其底面的輸入熱流密度qin可表示為：

式中：Q 為航空電子模塊的總功耗，本文考察4 種典型功耗，即Q=12，15，21和30 W。

儲熱器頂面的輸出熱流密度qout由自然對流熱流密度qnc和熱輻射熱流密度qrad兩部分組成，即：

其中：

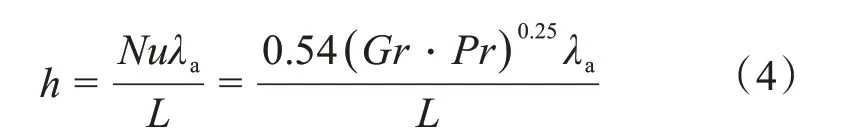
式中：h為儲熱器頂面的自然對流換熱系數；Ttop為儲熱器頂面的平均溫度；Tamb為環境溫度，本文取Tamb=333.15 K；λa為環境溫度下空氣的導熱系數；Nu、Gr和Pr分別為努賽爾數、格拉曉夫數和普朗特數，其具體計算公式詳見文獻［12］，計算這幾個無量綱準則數時采用環境溫度下空氣的物性參數，儲熱器特征尺寸均取L。

根據斯蒂芬-玻爾茲曼定律，熱輻射熱流密度qrad可表示為：式中：ε為儲熱器頂面的發射率，本文取ε=0.8。

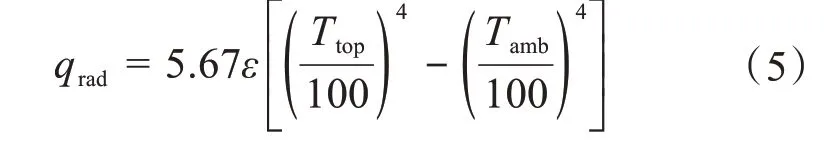
儲熱器穩態工作時，其底面的平均溫度與電子芯片的溫度直接相關。在實際應用中，由于熱阻的作用，前者略低于后者。考慮到安全余量，可直接將儲熱器底面的平均溫度視作溫度控制的目標溫度。本文定義從電子芯片開始產熱到儲熱器底面平均溫度達到設定溫度的時間為儲熱器的工作時間。

2 儲熱器工作時間預測的研究方法

2.1 數值模擬方法

本文采用焓-多孔介質法來模擬儲熱器單元體內部相變材料的二維瞬態熔化過程。在模擬相變材料的熔化過程時，考慮液相相變材料的自然對流流動，并假定該流動為層流。假設儲熱器內部相變材料的固相與液相之間不存在密度差異，其浮升力項中的密度按照包辛尼斯假設處理；金屬壁面內導熱過程為二維瞬態純導熱過程；忽略金屬壁面與相變材料之間的熱阻。儲熱器中相變材料區域的控制方程如表2所示。

表2 儲熱器中相變材料區域的控制方程Table 2 Governing equations of phase change material zone in heat storage device

表2 中：u、v 分別為x、y 方向的速度；p 為壓力；T為溫度；t為時間；ρP、μP、λP和CP分別為相變材料的密度、黏度、熱導率和比熱容；Su、Sv和ST分別為各控制方程的源項，其具體表達式如下：

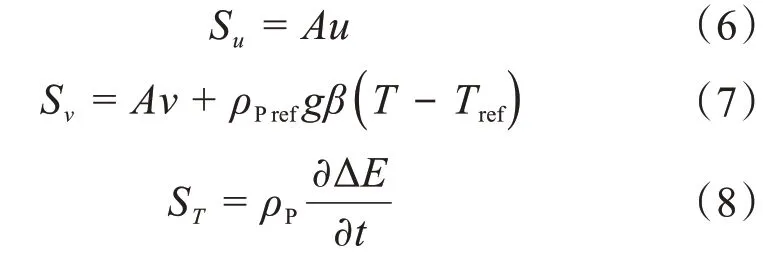
式中：g為重力加速度；β、E分別為相變材料的熱膨脹系數和焓；A為多孔系數；Tref為相變材料的參考溫度，本文中Tref的值為相變材料的初始溫度；ρPref為參考溫度下相變材料的密度［13］。

設置儲熱器單元體的邊界條件為：左、右兩側金屬壁面為對稱邊界；底面為恒熱流密度邊界，熱流密度大小由式（1）求得；當考慮自然對流和熱輻射時，頂面為變熱流密度邊界，熱流密度由式（2）至式（5）求得；當不考慮自然對流和熱輻射時，頂面為絕熱邊界。在數值模擬求解過程中，設相變材料的初始溫度Ti=343.15 K。

基于上述控制方程和邊界條件，在Fluent計算平臺上對儲熱器單元體內部相變材料的二維瞬態熔化過程進行數值模擬。在進行數值模擬前，先對采用的數值模擬方法的準確性進行驗證，驗證方法為文獻［14］中的方法，即用具有溫度場理論解的斯蒂芬問題來驗證本文采用的焓-多孔介質法的準確性。利用焓-多孔介質法求解經典的斯蒂芬問題，計算域大小為0.01 m×0.10 m。對同一時刻計算域長度方向溫度的數值模擬值與理論值［15］進行對比，結果如圖2 所示。從圖2 中可以看出，數值模擬值與理論值較吻合，兩者的最大誤差為0.54%，說明本文采用的數值模擬方法具有一定的準確性。

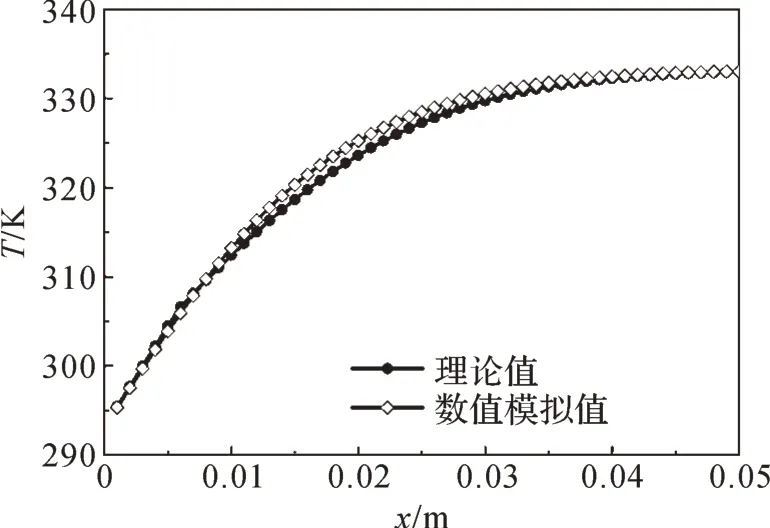
圖2 焓-多孔介質法的準確性驗證結果Fig.2 Ⅴerification results of accuracy of enthalpy-porous media method

2.2 線性回歸方法

航空電子模塊儲熱器的工作時間會隨功耗和設定溫度的變化而變化，可利用線性回歸方法對其進行預測。

當因變量Y隨2個自變量x1、x2變化時，二元線性回歸預測方程可表示為：

式中：Yi、x1i和x2i分別為Y、x1和x2的觀測數據。

為了考察二元線性回歸方法的預測精度，采用擬合優度R2進行評價，其表達式如下：

3 結果分析

3.1 儲熱器溫升及其相變材料熔化進程的規律

在不考慮儲熱器頂面自然對流和熱輻射（即頂面絕熱）時，4 種功耗下儲熱器底面平均溫度隨時間變化的曲線如圖3所示。從圖3中可以看出，隨著功耗的減小，相變材料熔化過程持續的時間延長，且在其熔化過程中儲熱器底面平均溫度的變化越平緩。在不同功耗下，在相變材料開始熔化前和熔化結束后，儲熱器底面的平均溫度均線性升高。

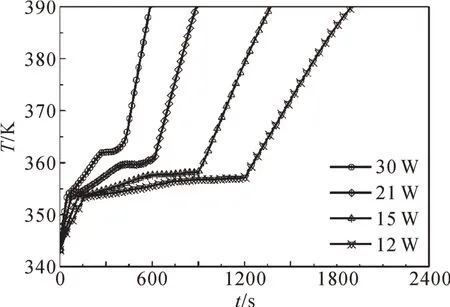
圖3 頂面絕熱時不同功耗下儲熱器底面的溫升曲線Fig.3 Temperature rise curves of bottom surface of heat storage device under different power consumptions with top surface insulation

在考慮儲熱器頂面自然對流和熱輻射（即頂面散熱）時，4 種功耗下儲熱器底面平均溫度隨時間變化的曲線如圖4所示。對比圖3和圖4可知，在相同功耗下，考慮頂面散熱時，儲熱器底面平均溫度的上升更為緩慢；在相變材料熔化結束后，儲熱器底面平均溫度的升高偏離線性變化，且功耗越小偏離程度越大。這是因為功耗越小，儲熱器頂面通過自然對流和熱輻射所散的熱量的占比越高，且自然對流和熱輻射并不恒定，隨著溫度的升高，通過自然對流和熱輻射所散的熱量越大，從而導致儲熱器底面的平均溫度上升越緩慢。

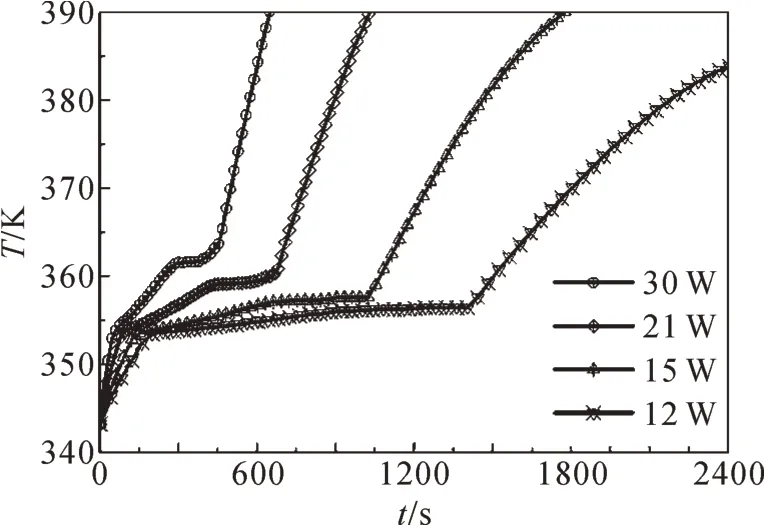
圖4 頂面散熱時不同功耗下儲熱器底面的溫升曲線Fig.4 Temperature rise curves of bottom surface of heat storage device under different power consumptions with top surface heat dissipation

為了深入了解相變材料的熔化進程，進一步考察2種情況（不考慮/考慮儲熱器頂面自然對流和熱輻射）下儲熱器內部相變材料的熔化過程。提取不同功耗下相變材料熔化過程中液相組分含量F的瞬態變化曲線，即相變材料熔化進程曲線，結果如圖5所示。其中液相組分含量F為相變材料熔化過程中液相體積與總體積的比值，F=0表示相變材料未開始熔化，F=1表示相變材料熔化結束。從圖5中可以看出，考慮頂面自然對流和熱輻射時，儲熱器內部相變材料熔化進程變慢，但當功耗為30 W時，儲熱器內部相變材料熔化進程的變慢程度并不明顯；當功耗減小為12 W 時，儲熱器內部相變材料熔化進程的變慢程度越來越顯著。

為了得到儲熱器工作時間的普遍性規律，本文對時間、功耗和溫度進行無量綱化。采用傅里葉數Fo作為時間的無量綱量，為：

式中：α為相變材料的熱擴散系數。

采用相變材料的初始溫度Ti及熔點溫度Tm（Tm=353.15 K）對溫度T進行無量綱化。定義無量綱溫度θ為：

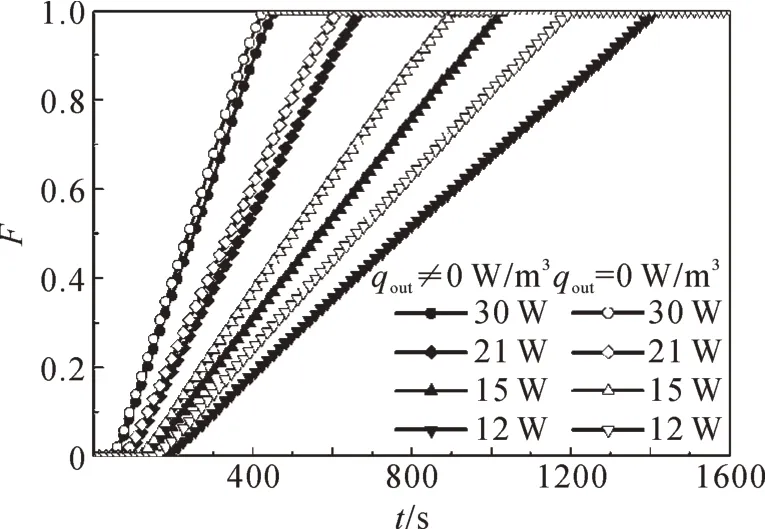
圖5 不同功耗下相變材料的熔化進程曲線Fig.5 Melting process curves of phase change material under different power consumptions

根據圖4所示的曲線，獲取考慮頂面自然對流和熱輻射時儲熱器在不同功耗及設定溫度下的工作時間。為了給下文的預測提供數據，從圖4的曲線中采樣并構建2組數據：一組包含20個數據，作為建模集，采樣功耗分別為30，21，15和12 W，采樣溫度分別為365，370，375，380和385 K；另一組包含16個數據，作為驗證集，采樣功耗分別為30，21，15 和12 W，采樣溫度分別為367.5，372.5，377.5和382.5 K。

3.2 儲熱器工作時間與功耗、設定溫度的關系

從上文結果可知，儲熱器的工作時間除了與功耗有關，還與設定溫度有關。為了準確預測儲熱器的工作時間，需分析其與功耗、設定溫度的關系。

3.2.1 工作時間與功耗的關系

從文獻［16-18］中可知，在不考慮儲熱器頂面自然對流和熱輻射時，在不同功耗下儲熱器內部相變材料熔化過程中，采用斯蒂芬數Ste 和瑞利數Ra 修正后，無量綱工作時間Fo與液相組分含量F 之間在不同功耗下具有相同的函數關系，即：

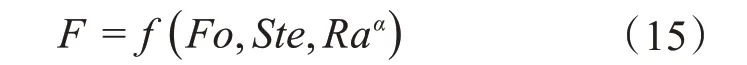
從文獻［16］中可知，斯蒂芬數Ste和瑞利數Ra與無量綱功耗ω 均呈正比，而α為常數。由此可見，當儲熱器內部相變材料的液相組分含量F確定時，由于F 與無量綱功耗ω 無關，則無量綱工作時間Fo 與無量綱功耗ω的（1+α）次方呈反比。換言之，在不考慮頂面自然對流和熱輻射時，儲熱器的工作時間與功耗呈指數關系。

根據上述分析可知，在考慮頂面自然對流和熱輻射的情況下，基于建模集中的20個數據，繪制無量綱工作時間Fo與無量綱功耗ω在單對數坐標（縱坐標為以10為底的對數坐標，橫坐標為線性坐標）下的依變關系曲線，結果如圖6所示。

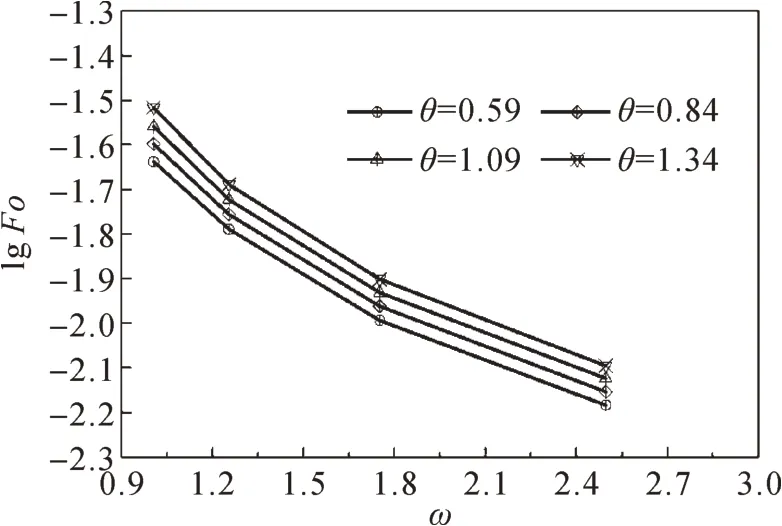
圖6 單對數坐標下Fo隨ω的變化規律Fig.6 Ⅴariation law of Fo with ω in single logarithmic coordinate

由圖6可知，在單對數坐標下，無量綱工作時間Fo與無量綱功耗ω之間不呈線性關系。這是因為在不考慮頂面自然對流和熱輻射時，輸入儲熱器單元體的凈熱量為定值；而在考慮頂面自然對流和熱輻射時，輸入儲熱器單元體的凈熱量隨溫度的升高而加速減小。因此，在圖6的基礎上，對無量綱功耗ω 也取對數，結果如圖7所示。

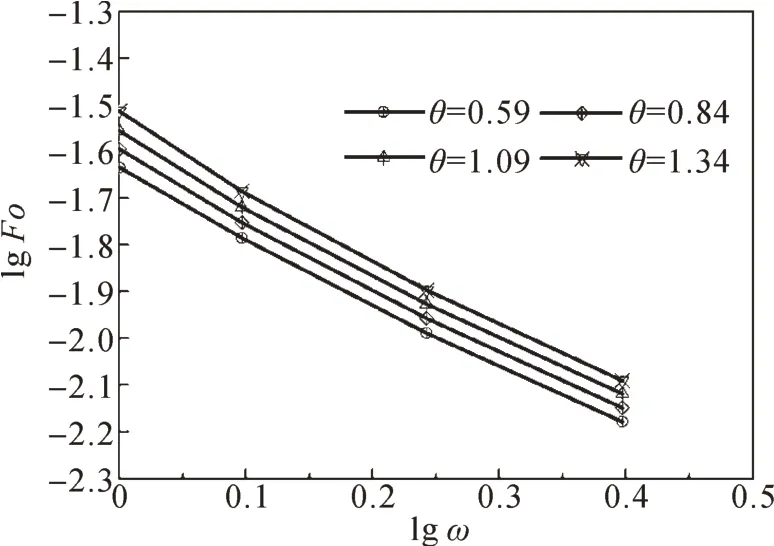
圖7 雙對數坐標下Fo隨ω的變化規律Fig.7 Ⅴariation law of Fo with ω in double logarithmic coordinate

從圖7中可以發現，在雙對數坐標下，無量綱工作時間Fo與無量綱功耗ω呈線性關系，且無量綱設定溫度θ 取不同值時，4 條變化曲線幾乎彼此平行。圖7所示的無量綱工作時間Fo與無量綱功耗ω之間的線性關系可近似用微分方程表示為：

3.2.2 工作時間與設定溫度的關系

從圖4中可看出，儲熱器內部相變材料熔化結束后，儲熱器底面平均溫度隨時間的變化曲線近似為對數曲線。因此，在考慮頂面自然對流和熱輻射的情況下，基于建模集中的20個數據，繪制無量綱工作時間Fo與無量綱設定溫度θ在單對數坐標下的依變關系曲線，結果如圖8所示。

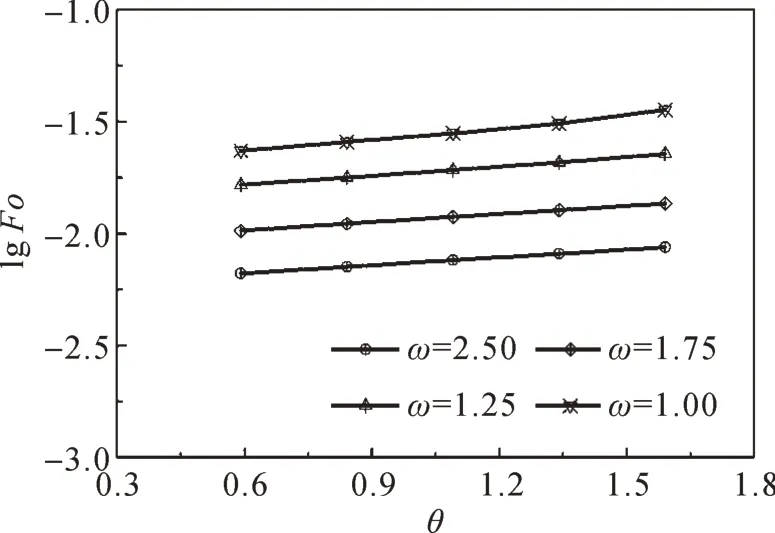
圖8 單對數坐標下Fo隨θ的變化規律Fig.8 Ⅴariation law of Fo with θ in single logarithmic coordinate

從圖8中可看出，在單對數坐標下，無量綱工作時間Fo 與無量綱設定溫度θ 幾乎呈線性關系，且無量綱功耗ω取不同值時，各條曲線幾乎平行，則無量綱工作時間Fo與無量綱設定溫度θ之間的線性關系可近似用微分方程表示為：

3.3 儲熱器工作時間的回歸預測

由此可見，可利用二元線性回歸方法對儲熱器工作時間進行預測。基于建模集中的20個數據，求解方程組（10），得到b0、b1和b2。本文運用R語言中的二元線性回歸函數來求解b0、b1和b2，最終得到的擬合關系式為：

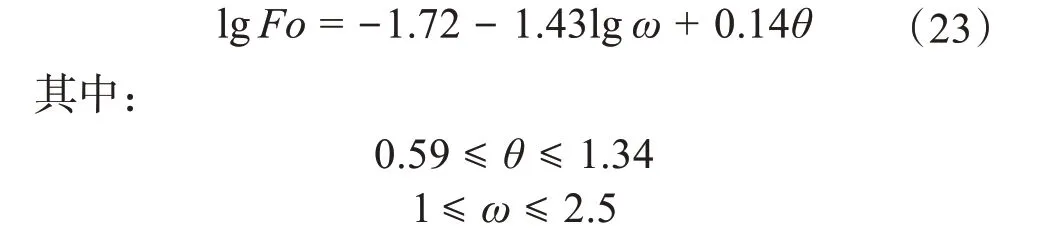
通過二元線性回歸擬合，得到建模集中20 個數據對應的lg Fo 的擬合值，并與對應的數值模擬值進行對比，結果如圖9 所示。從圖9中可以看出，20個lg Fo的擬合值非常接近其數值模擬值，且最大誤差在±4%以內，擬合優度R2=0.993。

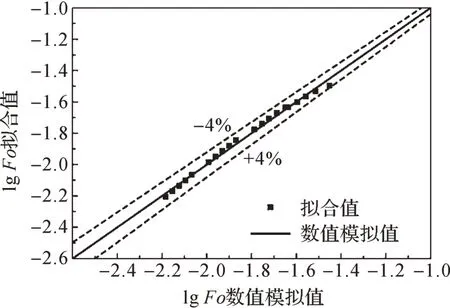
圖9 建模集中lg Fo的擬合值與數值模擬值對比Fig.9 Comparison of fitted values and numerical simulation values of lg Fo in the discovery set

為了驗證式（23）的預測精度，利用由16 個數據組成的驗證集進行驗證。利用式（23）計算驗證集中16個數據對應的lg Fo預測值，并與數值模擬值進行對比，結果如圖10所示。從圖10中可看出，式（23）的預測精度非常高，最大誤差為±3%。

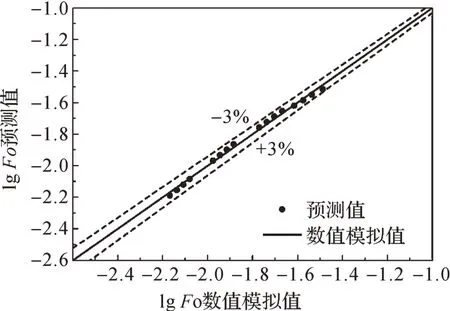
圖10 驗證集中lg Fo的預測值與數值模擬值對比Fig.10 Comparison of predicted values and numerical simulation values of lg Fo in the validation set

4 結束語

基于建立的航空電子模塊儲熱器在實際工作環境下的熱模型，利用數值模擬方法分析發現，儲熱器工作時間與功耗、設定溫度之間在對數坐標下呈線性關系，進而利用二元線性回歸法擬合得到儲熱器工作時間的預測公式。

基于擬合得到的儲熱器工作時間預測公式，設計人員可方便地計算出某一功耗和設定溫度下航空電子模塊儲熱器的工作時間，這對于彈載類短時工作的航空電子模塊的熱管理設計具有重要意義，可避免工程設計中不必要的、復雜的、非線性且多散熱路徑耦合的相變傳熱數值模擬。該預測公式可作為航空電子模塊儲熱器快速評估和敏捷開發的工具。但是，需要注意的是，該預測公式是在給定儲熱器尺寸下得到的，并未考慮尺寸變化的影響，后續研究中可對此進行完善。