雙邊錯位高速永磁直線同步電機的設計與分析

寇寶泉 葛慶穩(wěn) 張浩泉 牛 旭 黃昌闖

雙邊錯位高速永磁直線同步電機的設計與分析

寇寶泉 葛慶穩(wěn) 張浩泉 牛 旭 黃昌闖

（哈爾濱工業(yè)大學電氣工程及自動化學院 哈爾濱 150001）

針對傳統(tǒng)的4極6槽雙邊對稱長初級永磁直線同步電機，在保證電磁推力大小的情況下，提出采用雙邊錯位來降低永磁體渦流損耗的有效方法。介紹電機的基本結構，闡明雙邊錯位結構可以完全消除偶數(shù)次電樞諧波磁動勢，進而能大幅度降低次級永磁體渦流損耗。利用有限元分析（FEA）軟件對比分析對稱結構和錯位結構的定位力、電磁推力和次級渦流損耗，驗證錯位方法的正確性，并進行結構優(yōu)化設計。最后，研制一臺樣機并搭建實驗平臺，測得樣機的空載反電動勢、定位力以及靜推力。

雙邊錯位 永磁直線同步電機 分數(shù)槽集中繞組 永磁體渦流損耗

0 引言

20世紀90年代以來，電力電子技術的發(fā)展日趨成熟，用于電磁推進系統(tǒng)的直線電機逐漸成為研究的熱點[1-3]。雙邊長初級永磁直線同步電機效率高、推力密度大、法向力小、次級結構簡單質量輕、運行過程中不拖動電纜、安全可靠，非常適用于高速、高加速度場合。實際應用中，為了提高電機效率，減小對電源容量的要求，需要對長初級直線電機進行分段。采用分數(shù)槽集中繞組便于分段，初級可以模塊化加工，同時具有槽利用率高、齒槽定位力小、線圈端部短、銅耗少和空載反電動勢（back- Electromotive Force, back-EMF）波形正弦性好等一系列優(yōu)點[4-7]。但是分數(shù)槽集中繞組的電樞磁動勢諧波含量比較大，特別是高速場合，這些諧波磁動勢相對于次級高速運動，進而在永磁體內感應出渦流，產生附加的渦流損耗，使得永磁體溫度升高，甚至引起退磁[8-9]。

為了降低永磁體渦流損耗，國內外學者提出了多種方法[10-16]，如增大氣隙長度、減小槽口寬度、永磁體分塊以及在永磁體外增加保護套和高電導率的屏蔽環(huán)。文獻[17]提出采用多層繞組來消除低次空間諧波磁動勢。文獻[18-19]通過在定子齒部或者定子軛部放置不導磁材料來減小低次諧波磁動勢幅值。上述方法可以降低永磁體渦流損耗，但都對電機的推力性能產生較大的不利影響。

本文針對4極6槽雙邊對稱長初級永磁直線同步電機（Double-Sided Symmetrical Long Primary- Permanent Magnet Linear Synchronous Motor, DSSLP- PMLSM）提出一種新的結構方案，其雙邊初級鐵心一側的齒對應另一側的槽，且沿運動方向，雙邊初級繞組錯位布置。這樣在保證電機推力大小的情況下，可以消除幅值比較大的電樞磁動勢諧波，使得次級永磁體渦流損耗得到大幅度下降。

1 電機的基本結構

圖1為傳統(tǒng)4極6槽DSSLP-PMLSM基本結構。圖2為提出的雙邊錯位長初級永磁直線同步電機（Double-Sided Dislocation Long Primary-Permanent Magnet Linear Synchronous Motor, DSDLP-PMLSM）基本結構。電機主要由初級和次級兩部分組成，初級包括初級鐵心和兩套初級繞組，次級包括基板和永磁體。

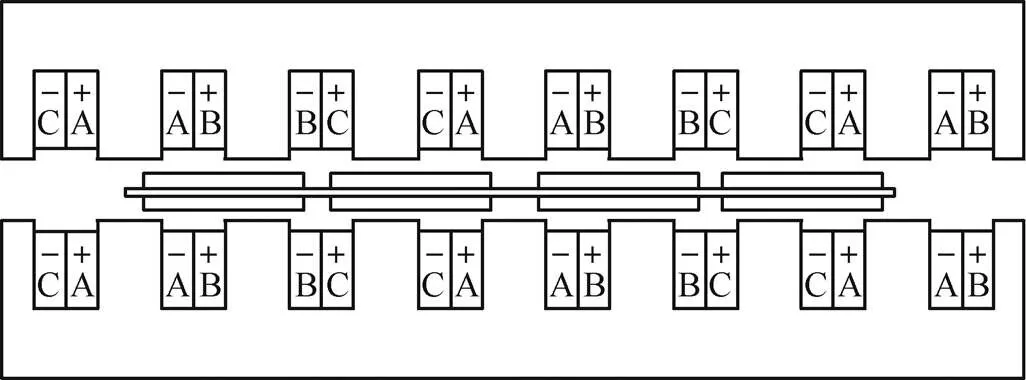
圖1 DSSLP-PMLSM基本結構

雙邊初級形成串聯(lián)磁路，兩套繞組對應相串聯(lián)連接。相比于傳統(tǒng)對稱結構，DSDLP-PMLSM的主要特點：①初級寬等于槽寬，雙邊鐵心一側的齒與另一側的槽相對；②兩套繞組不是對稱布置，對應相之間錯了一個極距，并且反向連接。

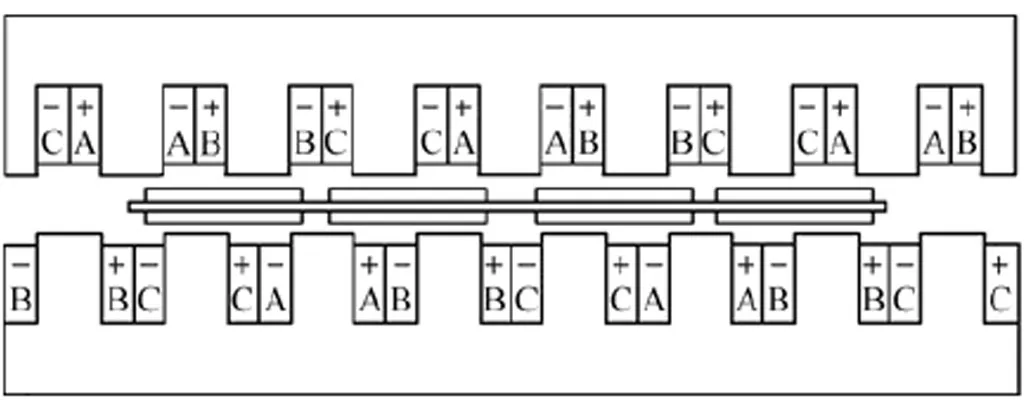
圖2 DSDLP-PMLSM基本結構

2 電樞磁動勢分析

4極6槽電機由兩個2極3槽單元電機組成。對于2極3槽單元電機，根據(jù)單元電機三相合成磁動勢相關公式[5]，以基波幅值作為基值，把其他各次磁動勢的幅值與此基值相比進行標幺化，單元電機前30對極的諧波分析結果如圖3所示。由圖可見，電機內部主要的電樞諧波磁動勢為2次，其幅值為基波的一半。

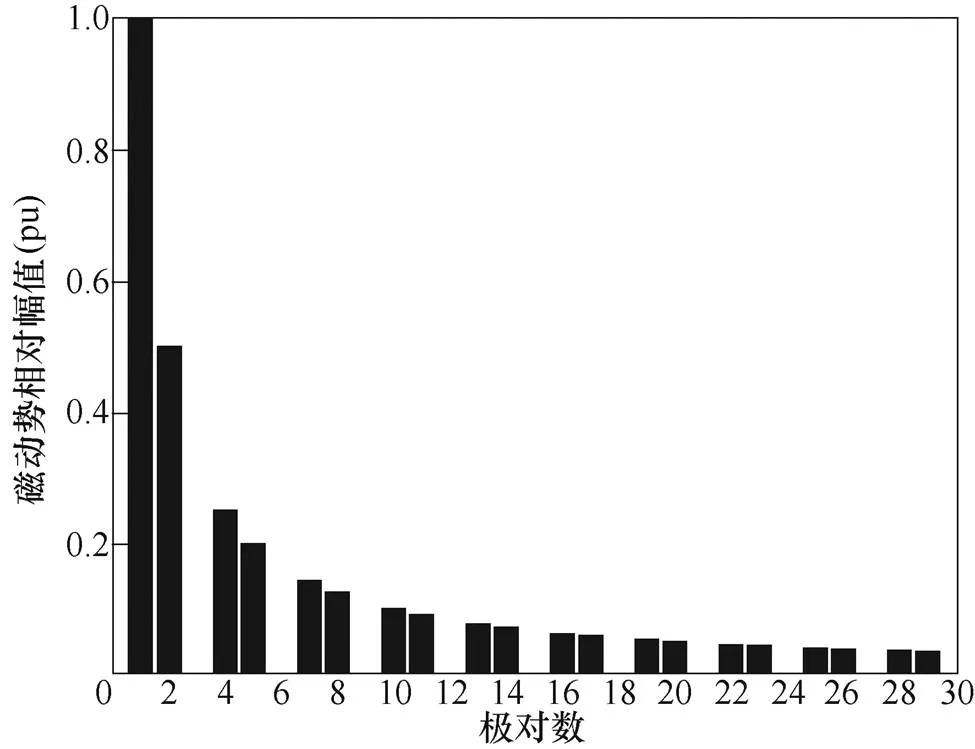
圖3 2極3槽單元電機磁動勢諧波分析

DSSLP-PMLSM兩套繞組各線圈空間位置相同，其產生的電樞磁動勢也相同，電機內部會同時存在偶數(shù)次和奇數(shù)次諧波磁動勢，磁動勢諧波含量大。

基波磁動勢波長為2（為電機極距），諧波磁動勢波長為

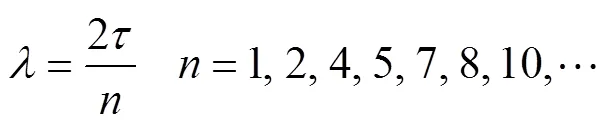
首先，當上下同相繞組之間相錯一個極距時，不難發(fā)現(xiàn)，錯位距離是偶數(shù)次諧波波長的整數(shù)倍，是奇數(shù)次諧波半個波長的奇數(shù)倍。然后，當上下同相繞組反向連接時，偶數(shù)次諧波正好正負疊加，完全消除，奇數(shù)次諧波空間分布完全相同，正好正正疊加。

為了驗證上述方法的有效性，選取同相相互錯位的兩個單線圈為對象，分析DSDLP-PMLSM的電樞磁動勢。根據(jù)磁通連續(xù)性原理，可得到兩個單線圈的磁動勢分布，然后選取空間位置為橫坐標，對其進行傅里葉分解，進而可得到各次諧波磁動勢分量，如圖4所示（圖中僅繪出前7次的諧波分量）。從圖可見，相互錯位的兩個同相線圈產生的各次諧波磁動勢有所差異，1、5、7次諧波磁動勢分量空間分布相同，2、4次諧波磁動勢分量空間分布正好反向。同理不難發(fā)現(xiàn)，包含基波在內的所有奇數(shù)次諧波磁動勢空間分布都相同，所有偶數(shù)次諧波磁動勢空間分布都相反，所以此兩個線圈最終的合成磁動勢中僅含有奇數(shù)次諧波磁動勢，偶數(shù)次諧波磁動勢被完全消除，并且對基波磁動勢沒有產生影響。

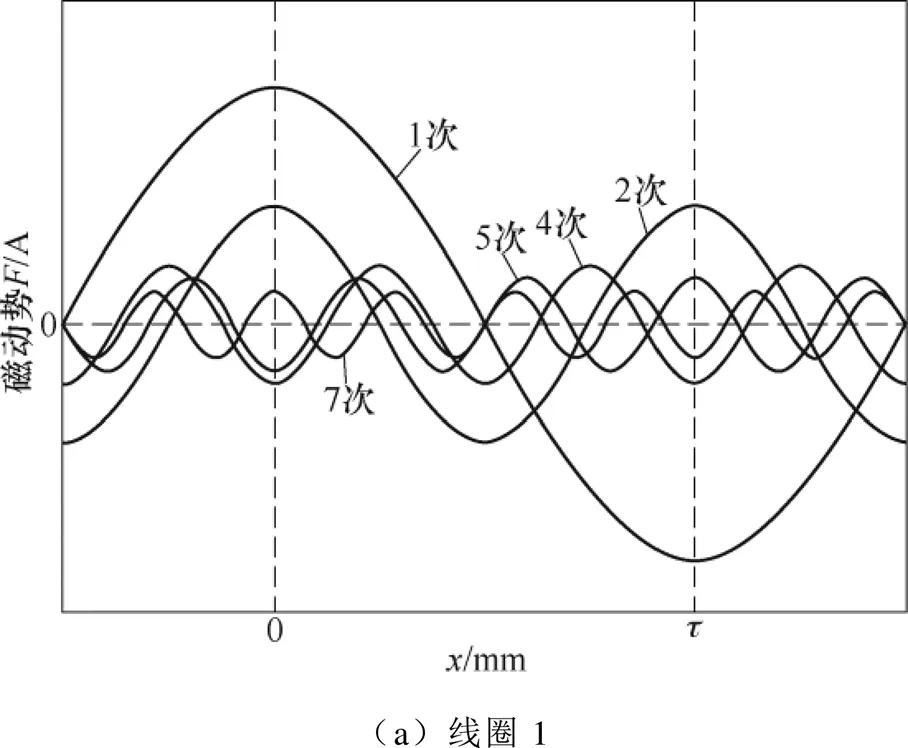
實際上對于傳統(tǒng)的4極6槽永磁直線同步電機，它的初級繞組在N極和S極下的分布不同，使得N極和S極下的磁動勢幅值不相等，所以其磁動勢波形中除了含有奇數(shù)次諧波外，還含有偶數(shù)次諧波。而本文使上下兩套繞組錯位的目的就是在初級的一側去構造另一側每相繞組的負相帶，這樣就會使N極和S極下的電樞磁動勢相等、相反，所以電機電樞磁動勢除基波外，僅含有奇數(shù)次諧波。

3 永磁體渦流損耗解析計算

當不考慮電流時間諧波時，對于永磁直線同步電機來說，永磁體渦流損耗產生的主要原因是初級鐵心開槽和存在電樞磁動勢空間諧波。在求解永磁體上的渦流損耗時作如下假設：①忽略初級鐵心飽和的影響；②不考慮永磁體渦流的反作用；③永磁體相對磁導率為1；④分析區(qū)域在二維平面內，不考慮電機的端部效應；⑤假設雙邊初級之間的磁力線都是垂直直線。

3.1 氣隙磁導分析

以雙邊對稱永磁直線同步電機為例分析電機的氣隙磁導，DSSLP-PMLSM的初級鐵心如圖5所示。

圖5 DSSLP-PMLSM的初級鐵心

比磁導表達式為

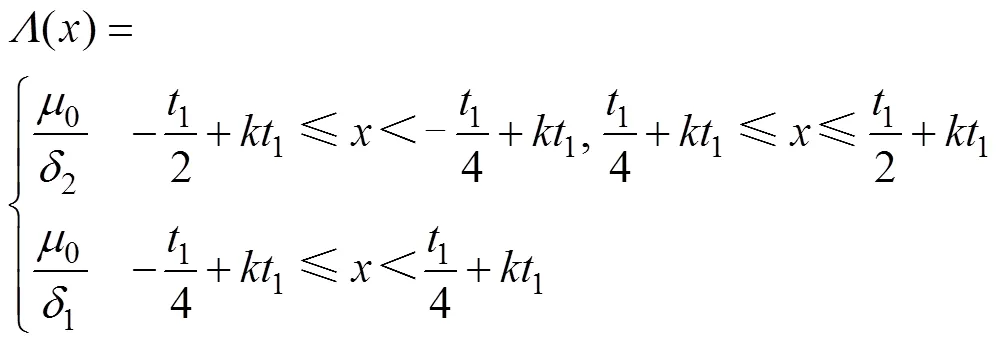
式中，0為真空磁導率；1、2分別為雙邊齒之間和槽之間的距離；1為齒距；為整數(shù)。

由式（2）可得比磁導的傅里葉表達式為

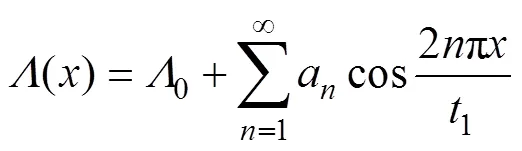
其中

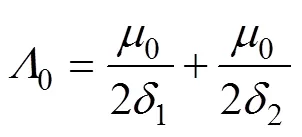
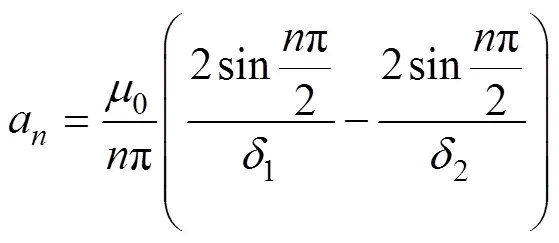
式中，為比磁導諧波階數(shù)。

3.2 空載氣隙磁場的計算

由文獻[20]可知，永磁體磁動勢傅里葉級數(shù)可表示為

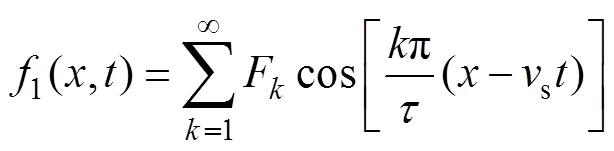
其中

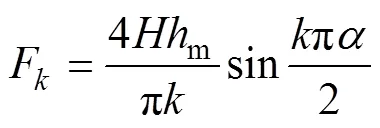
式中，為永磁體的矯頑力；s為同步速度；m為永磁體厚度；為計算極弧系數(shù)。

根據(jù)磁路的歐姆定律，空載氣隙磁場可表示為

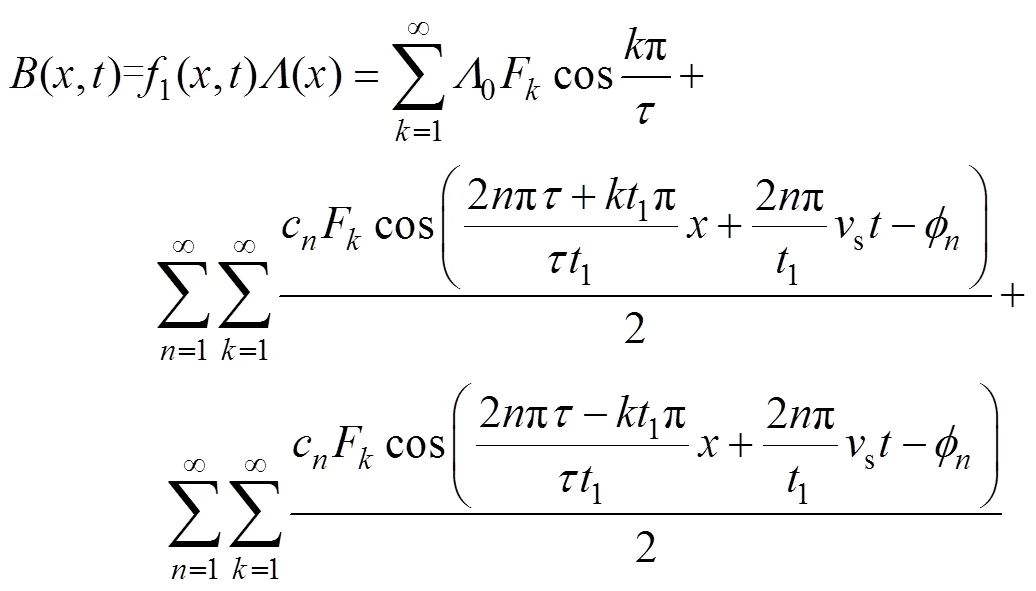
式中，c、分別為第次比磁導諧波的幅值和初始相位。

3.3 電樞氣隙磁場的計算

由文獻[6]關于分數(shù)槽集中繞組磁動勢的分析，可進一步推導出傳統(tǒng)雙邊永磁直線同步電機以及本文提出的雙邊錯位永磁直線同步電機的電樞磁動勢表達形式。

雙邊對稱永磁直線同步電機的電樞磁動勢可表示為

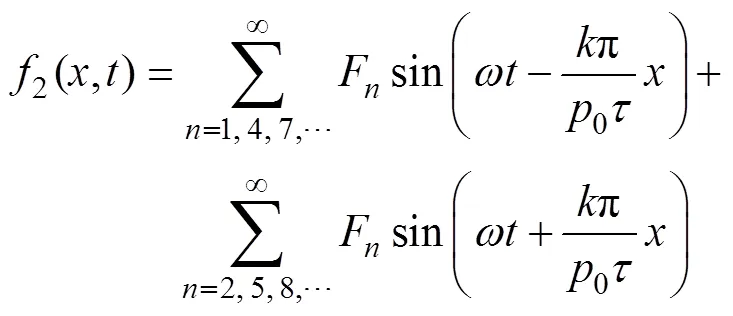
其中

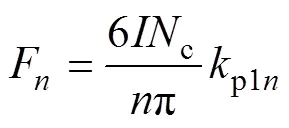
式中，0為單元電機的極對數(shù)；為電樞電流幅值；c為單個線圈的匝數(shù)；p1n為極對數(shù)為的諧波繞組短距系數(shù)。

同理，雙邊錯位永磁直線同步電機的電樞磁動勢的表達式為

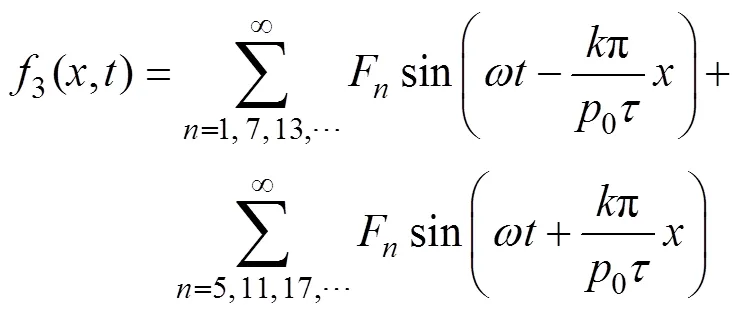
其中

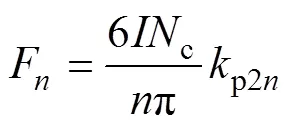
式中，p2n為DSDLP-PMLSM的繞組系數(shù)。

同理，再根據(jù)磁路的歐姆定律就可以計算出電樞氣隙磁場。

3.4 永磁體渦流損耗的求解

上文已經(jīng)分別求解出空載氣隙磁場和電樞氣隙磁場，首先根據(jù)磁矢位與的關系

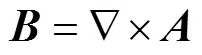
計算出磁矢位。然后計算出永磁體中的渦流密度為

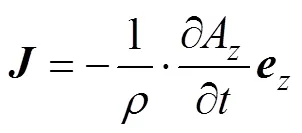
式中，為永磁體的電阻率。

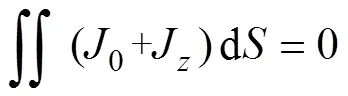
最后根據(jù)焦耳定律，可得永磁體內的渦流損耗為

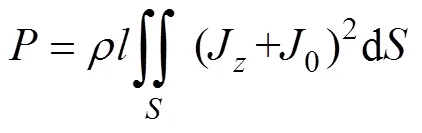
式中，為永磁體的橫向長度。

4 DSDLP-PMLSM的有限元分析

為了驗證雙邊錯位結構和解析模型的有效性，利用有限元軟件對雙邊錯位永磁直線同步電機的定位力、電磁推力和次級永磁體渦流損耗進行分析，并對其結構進行優(yōu)化。

4.1 定位力及電磁推力

長初級永磁直線同步電機的定位力主要成分是齒槽定位力。在一個機械周期內，分數(shù)槽永磁直線同步電機的齒槽定位力的周期數(shù)等于槽數(shù)與極數(shù)的最小公倍數(shù)[5]。圖6為兩種結構的定位力對比曲線。從圖中可知，在一個電周期（20ms）內定位力都是波動6次，對稱結構的定位力幅值為102N，錯位結構的定位力為110N，增加了約8%，錯位結構對定位力的影響很小，并且不會改變齒槽定位力的周期。

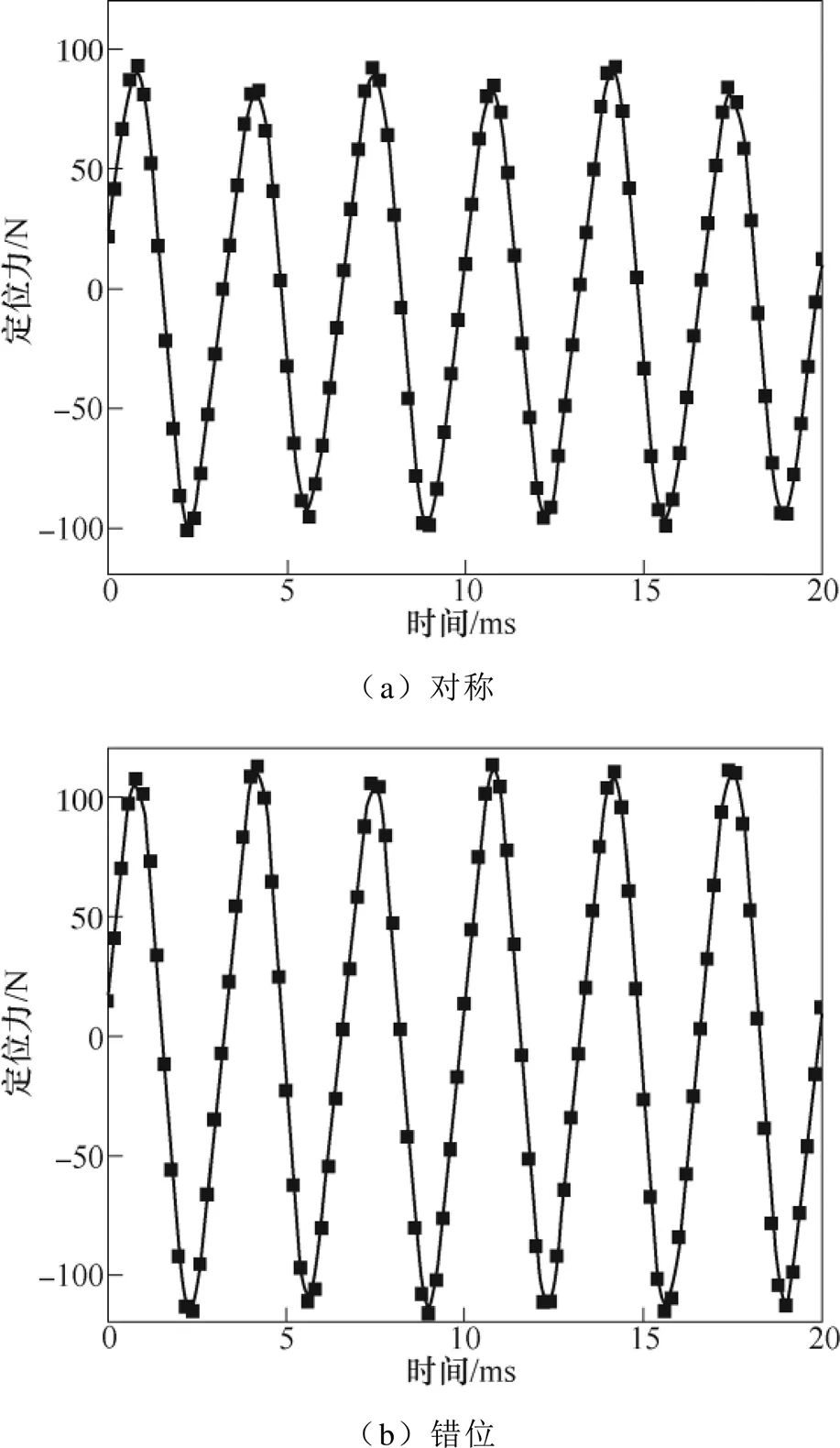
圖6 定位力對比曲線

圖7為相同工況下兩種結構的電磁推力對比曲線。從圖中可知，兩種結構電磁推力隨時間的變化曲線相差不大，錯位結構的平均電磁推力略小于對稱結構。對稱結構的平均電磁推力為596N，錯位結構的平均電磁推力為566N，約降低了5%，錯位結構對電機電磁推力的影響也很小。這是由于錯位結構對電樞基波磁動勢沒有影響，只是磁路的等效氣隙長度稍有增加，使得錯位結構的電磁推力稍有降低。

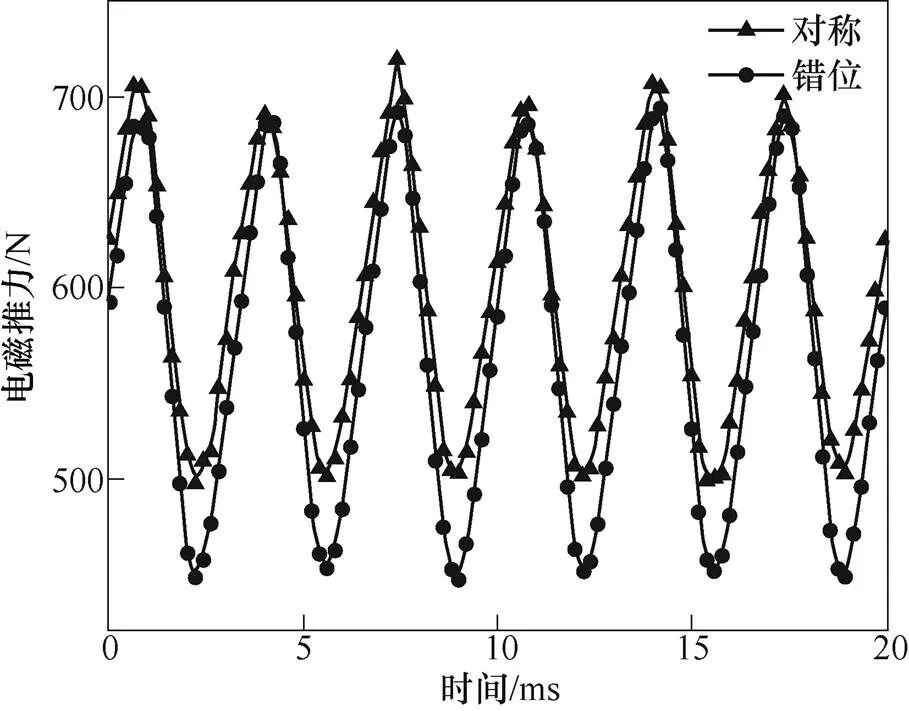
圖7 電磁推力對比曲線

4.2 永磁體渦流損耗

圖8為錯位結構的電樞反應氣隙磁通密度以及對應的諧波分析結果。從圖中可知，電樞磁場呈對稱分布，不含有偶數(shù)次諧波，主要的諧波磁場為5次和7次，這與第2節(jié)關于電樞磁動勢的分析相一致。

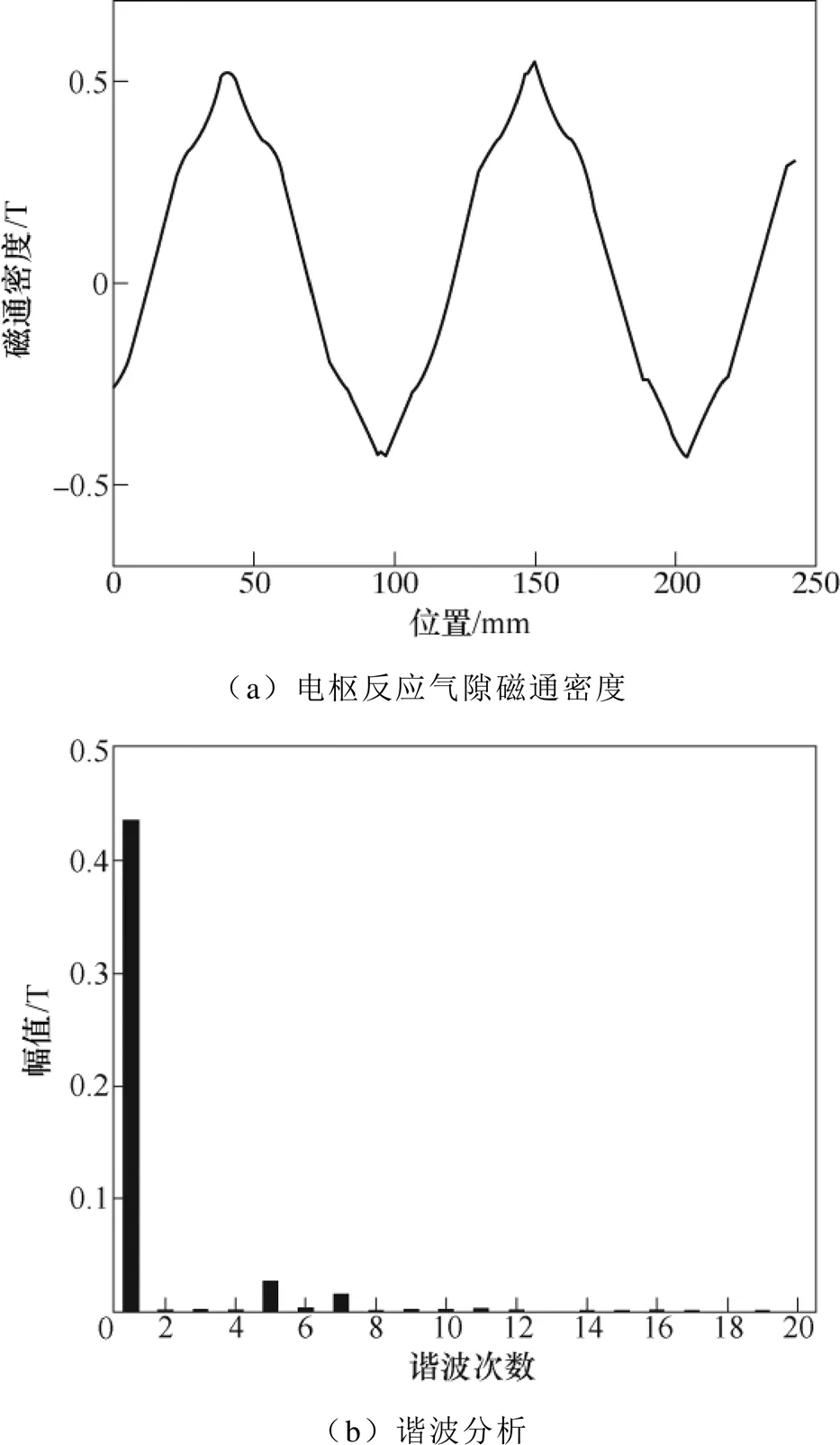
圖8 電樞反應氣隙磁通密度及其諧波分析

電機電樞諧波磁動勢將產生對應的諧波磁場。諧波磁場相對于永磁體高速運動，會在永磁體內感應出渦流，進而產生渦流損耗。圖9為兩種結構的永磁體渦流損耗對比曲線。從圖中可知，對稱結構的永磁體渦流損耗平均值為36.1W，錯位結構為5.6W，降低了近84.5%；此外，對稱結構的解析結果為37.8W，與仿真結果相比誤差為4.7%；錯位結構的解析結果為5.1W，與仿真結果相比誤差為8.9%。可見，對稱結構的解析精度要高于錯位結構，這是因為對于錯位結構，利用式（3）計算的比磁導是一個恒定的常數(shù)，也就無法計算出由于初級鐵心開槽引起的渦流損耗，從而使得解析結果偏小。

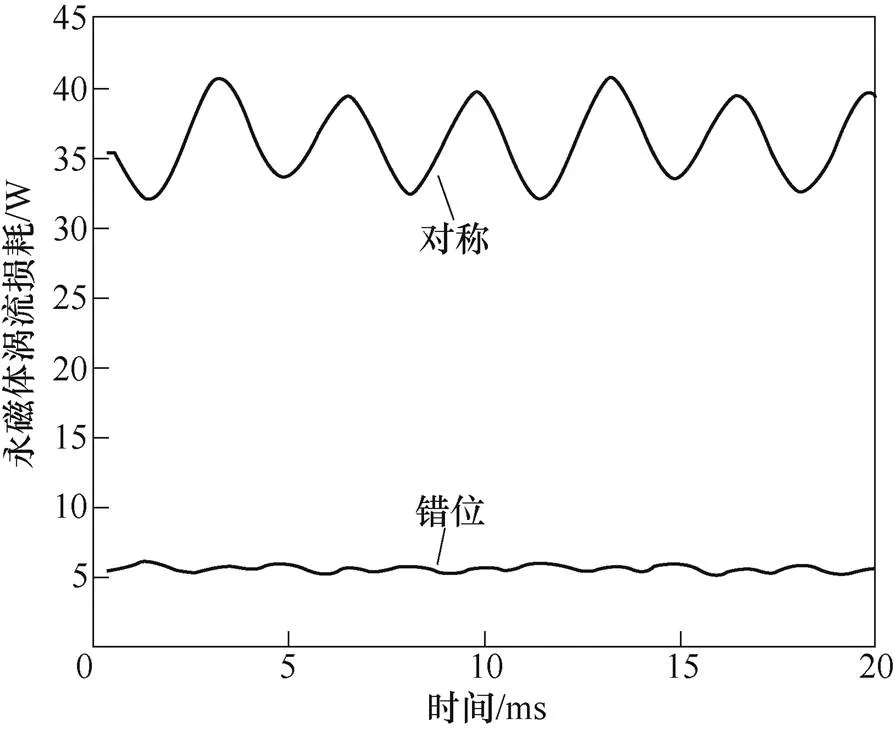
圖9 永磁體渦流損耗對比曲線

另一方面，在一個電周期內對稱結構的永磁體渦流損耗波動了6次，錯位結構波動了12次，其主要的諧波次數(shù)提高了1倍。這正是由于錯位結構中的電樞磁動勢諧波次數(shù)也提高了一倍。

圖10為永磁體渦流損耗分布。從圖中可知，對于對稱結構，基板兩側的永磁體渦流呈對稱分布，錯位結構基板兩側的永磁體渦流損耗分布不同，錯位結構可以有效地降低永磁體渦流損耗。

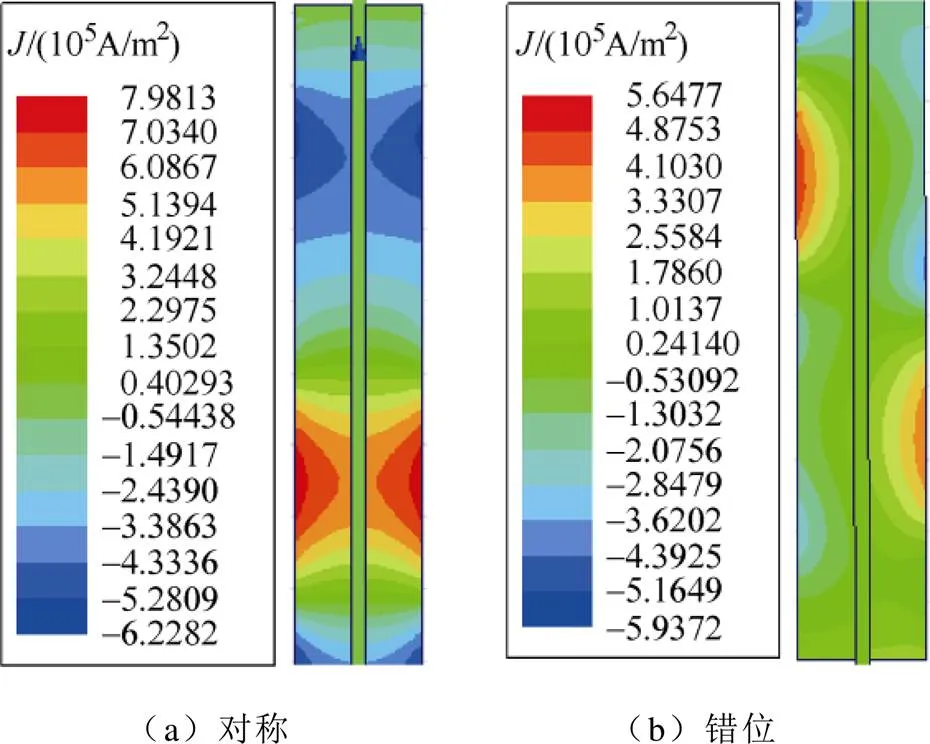
圖10 永磁體渦流損耗分布

4.3 次級基板材料分析

次級基板位于兩側永磁體的中間，是勵磁磁場磁路的一部分，為了提高電機的推力密度，一般基板都選用鐵磁材料。鐵磁材料密度大、質量重。但是應用于電磁推進系統(tǒng)的直線電機要求能獲得較大的加速度，需要盡可能地減小次級的質量，可選擇密度小、質量輕的鋁合金材料。圖11為次級基板選用這兩種材料下的電磁推力對比曲線。從圖中可知，使用10號鋼材料的電磁推力要略大于鋁合金材料，使用鋁合金的電磁推力相比于使用10號鋼降低了約10%。

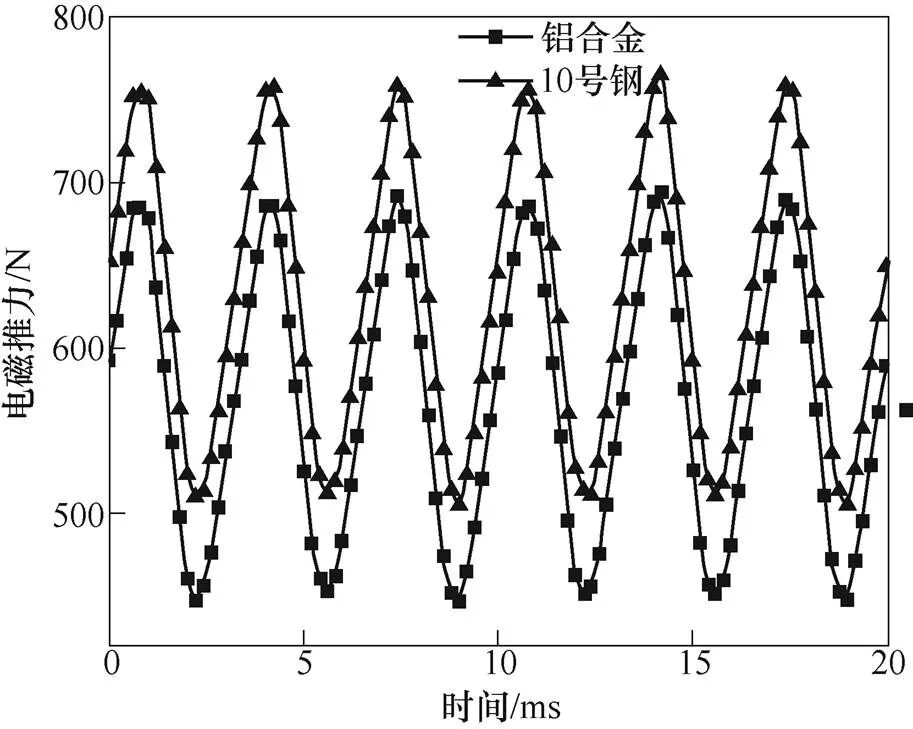
圖11 不同材料下的電磁推力

圖12為次級基板選用不同材料下的永磁體渦流損耗對比曲線。從圖中可知，使用10號鋼材料的永磁體渦流損耗遠大于鋁合金材料，使用鋁合金的渦流損耗相比于10號鋼降低了約86.5%。這是由于10號鋼相比于鋁合金材料磁路磁阻要小，使電機氣隙磁場變大，同時也會使磁導諧波幅值變大，從而會增加永磁體上的渦流損耗。可見，次級基板選用鋁合金材料，能夠有效降低永磁體渦流損耗。綜合考慮，次級基板選用鋁合金材料。

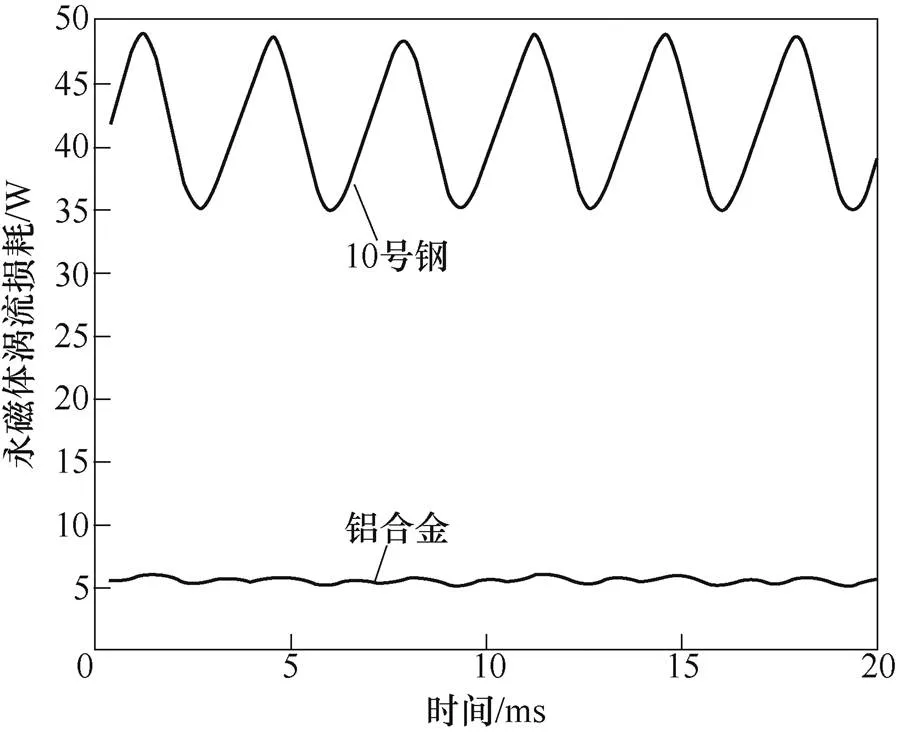
圖12 不同材料下的永磁體渦流損耗

5 DSDLP-PMLSM的實驗

在上述分析的基礎上，以提高永磁體利用率、電磁推力和降低推力波動為目的，利用有限元軟件對電機極弧系數(shù)、永磁體斜極角度進行優(yōu)化，并根據(jù)優(yōu)化結果設計了一臺樣機，樣機具體參數(shù)見表1。表中的永磁體極對數(shù)指的是初級和次級耦合長度內的永磁體對數(shù)。

表1 DSDLP-PMLSM樣機參數(shù)

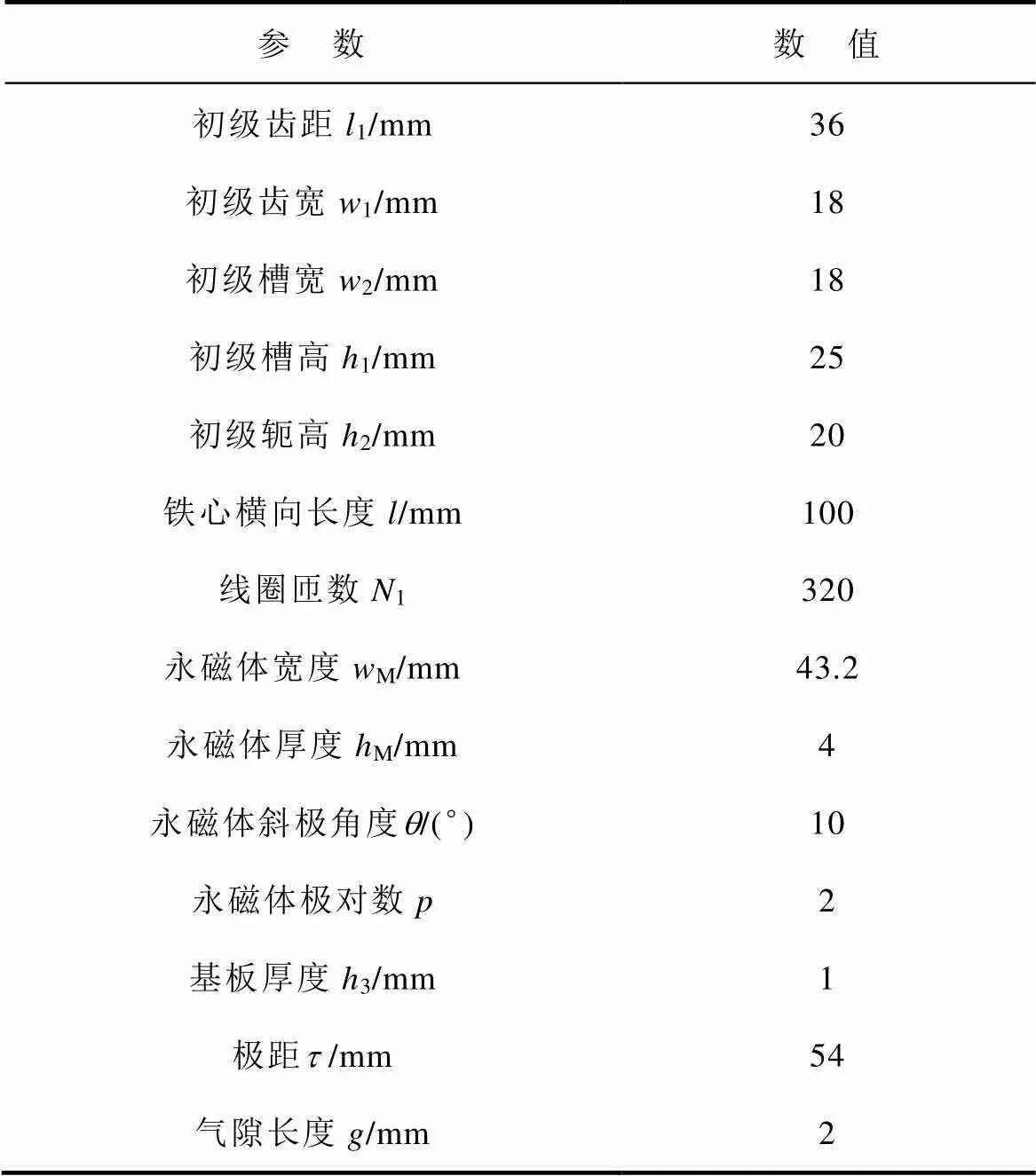
Tab.1 The parameters of prototype DSDLP-PMLSM

樣機結構如圖13所示。電機鐵心采用硅鋼片疊壓而成，通過螺絲與鋼板底座緊密相連，如圖13a所示。次級永磁體嵌在鋁合金基板的平行四邊形凹槽內，如圖13b所示。整個次級部分通過滑塊與安裝在兩側鋼板上的導軌連接，如圖13c所示。

圖13 樣機結構

為了測得電機的定位力、空載反電動勢和靜推力，搭建了如圖14所示的實驗平臺。

圖14 實驗平臺

5.1 空載反電動勢

伺服電動機和滾珠絲杠產生的恒定推力帶動次級沿導軌做勻速運動，用示波器測量三相繞組產生的空載反電動勢。由于電機初級長度有限，為了防止次級運動過快發(fā)生脫落，在實驗過程中只對低速下的空載反電動勢進行測量。圖15所示為在0.34m/s速度下的空載反電動勢測試結果。圖16為樣機實測數(shù)據(jù)與有限元計算結果的對比，實驗得到的空載反電動勢幅值為49.6V，有限元計算得到的結果為48.4V，兩者結果很接近，誤差為2.4%，實驗結果證明了有限元計算的正確性。

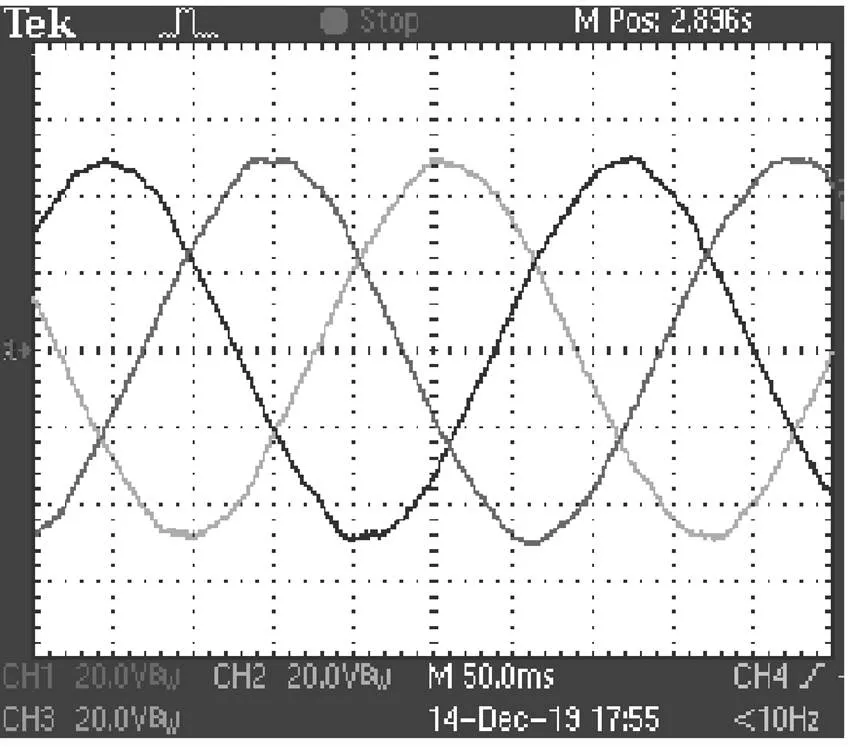
圖15 樣機空載反電動勢

5.2 定位力

在電機空載情況下，用伺服電動機帶動滾珠絲杠推動電機勻速運動。通過拉壓力傳感器檢測定位力變化，結果如圖17所示。從圖中可知，定位力在一個電周期內波動6次，與有限元仿真結果相同。實驗測得樣機定位力幅值為12N（見圖中1V對應5N），有限元計算結果為11N。

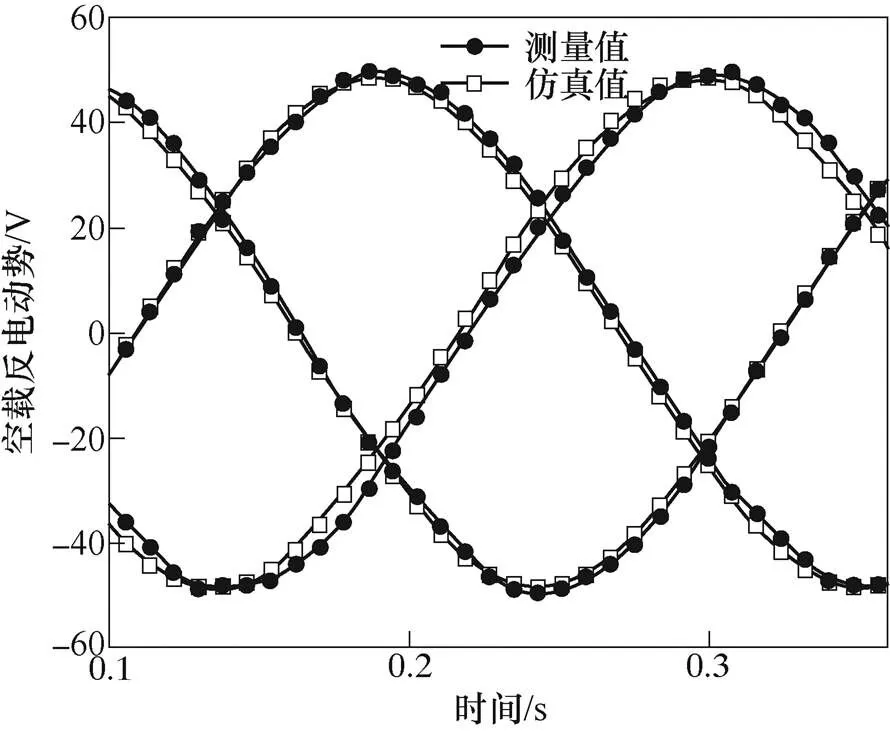
圖16 空載反電動勢結果對比

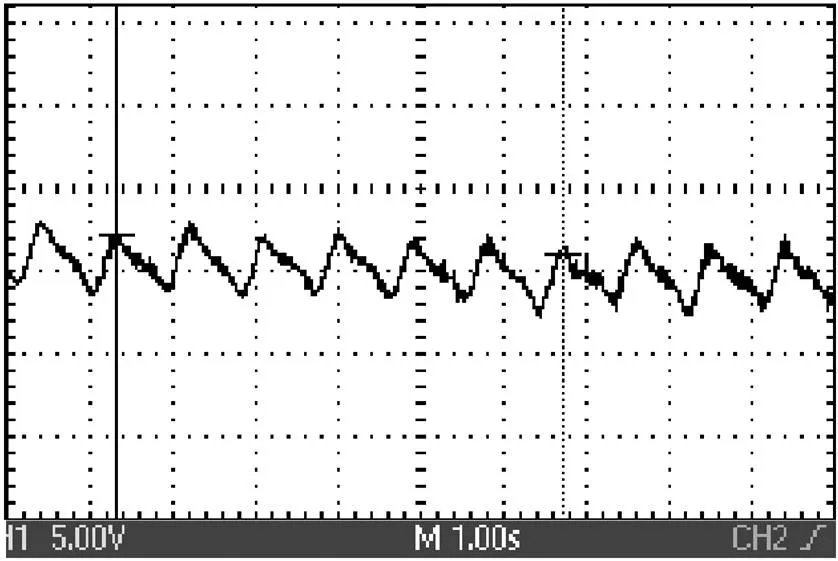
圖17 樣機定位力實驗結果

5.3 靜推力

給電樞繞組其中一相通入直流電流，用伺服電動機和滾珠絲杠帶動樣機次級做勻速直線運動，此時直線電機力的變化就是電機的靜推力特性。

實驗測試過程中，給A相繞組通入直流電流，然后改變電流的大小，得到電機靜推力與通電電流的關系曲線。圖18為A相繞組通入4A直流電流時電機靜推力隨空間位置的變化曲線（見圖中1V對應50N）。圖19為電機靜推力與通電電流的關系曲線，兩條曲線基本重合，最大誤差為2.6%。對于圖19，需要說明的是，由于直流電源功率的限制，沒有能測量電機飽和狀態(tài)下的靜推力。

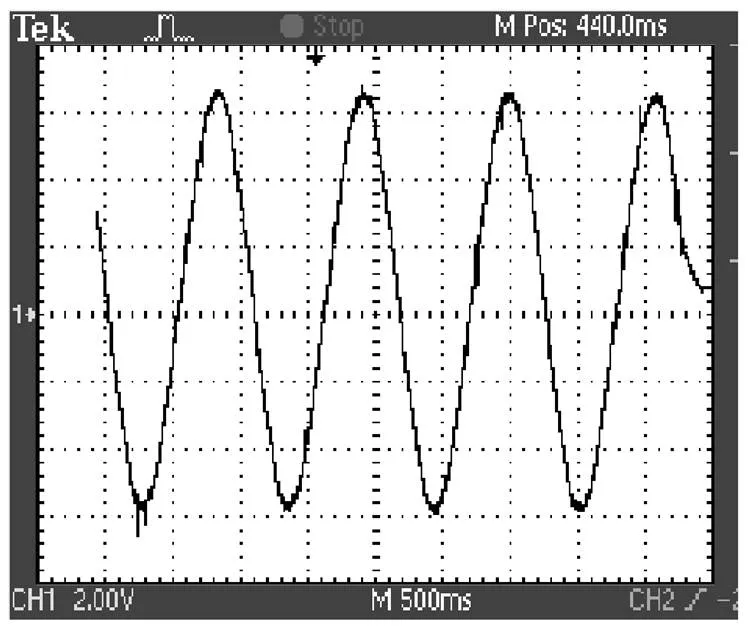
圖18 樣機靜推力實驗結果

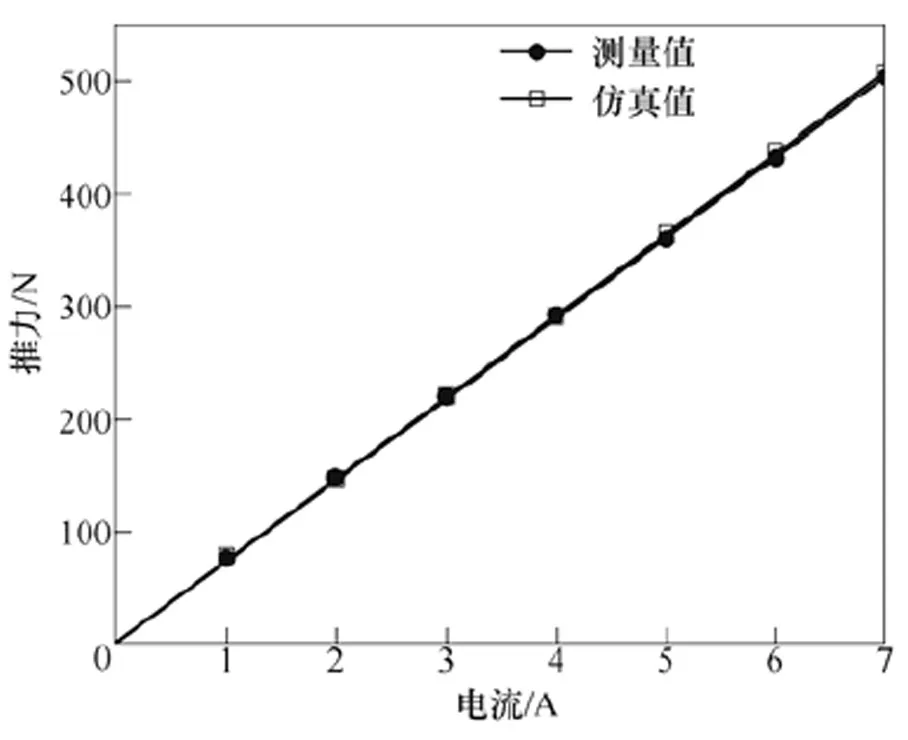
圖19 樣機靜推力與通電電流的關系

6 結論

本文針對4極6槽雙邊對稱長初級永磁直線同步電機，提出一種雙邊錯位結構，采用雙邊錯位的方法對電機電樞磁動勢諧波進行削弱。首先，分析了雙邊錯位結構的電樞磁動勢，推導永磁體渦流損耗的計算公式，并利用有限元軟件與雙邊對稱結構分別從定位力、電磁推力和永磁體渦流損耗進行對比分析。結果表明，雙邊錯位結構相比于雙邊對稱結構，電樞諧波磁動勢僅存在奇數(shù)次，偶數(shù)次被完全消除；雙邊錯位結構對電機的定位力和電磁推力影響都很小，使電機定位力增加了約8%，電磁推力下降了5%左右，永磁體渦流損耗下降了近84.5%，該結構可以在保證電磁推力的情況下有效降低永磁體渦流損耗；雙邊對稱結構的解析誤差為4.7%，錯位結構的解析誤差為8.9%。其次，對次級基板材料的選取進行了分析，采用鋁合金材料可以有效降低永磁體上的渦流損耗。最后，研制了一臺雙邊錯位永磁直線同步電機樣機并進行初步的實驗研究，實驗結果與有限元計算結果很相近，空載反電動勢誤差為2.4%，靜推力最大誤差為2.6%。

[1] Laithwaite E R. Adapting a linear induction motor for the acceleration of large masses to high velocities[J]. IEE Proceedings-Electric Power Applications, 1995, 142(4): 262-268.

[2] Fair H D. The science and technology of electric launch[J]. IEEE Transactions on Magnetics, 2001, 37(1): 25-32.

[3] 杜超, 孟大偉. 基于場路結合法的電磁彈射用新型永磁直線同步電機的研究[J]. 電機與控制學報, 2019, 23(9): 65-74.

Du Chao, Meng Dawei. Investigation of permanent magnet linear synchronous motor for electromagnetic launch based on field-circuit combined method[J]. Electric Machines and Control, 2019, 23(9): 65-74.

[4] 莫會成. 分數(shù)槽繞組與永磁無刷電動機[J]. 微電機, 2007, 40(11): 39-42.

Mo Huicheng. Fractional-slot winding and PM brush- less motor[J]. Micromotors, 2007, 40(11): 39-42.

[5] 譚建成. 三相無刷直流電動機分數(shù)槽集中繞組槽極數(shù)組合規(guī)律研究[J]. 微電機, 2007, 40(12): 72-77.

Tan Jiancheng. Investigation on slot/pole number combinations for 3-phase BLDCM with concentrated windings[J]. Micromotors, 2007, 40(12): 72-77.

[6] 陳益廣, 潘玉玲, 賀鑫. 永磁同步電機分數(shù)槽集中繞組磁動勢[J]. 電工技術學報, 2010, 25(10): 30-36.

Chen Yiguang, Pan Yuling, He Xin. Magnetomotive force in permanent magnet synchronous machine with concentrated fractional-slot winding[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 30-36.

[7] 鮑曉華, 劉佶煒, 孫躍, 等. 低速大轉矩永磁直驅電機研究綜述與展望[J]. 電工技術學報, 2019, 34(6): 1148-1160.

Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.

[8] Ishak D, Zhu Zhiqiang, Howe D. Eddy-current loss in the rotor magnets of permanent-magnet brushless machines having a fractional number of slots per pole[J]. IEEE Transactions on Magnetics, 2005, 41(9): 2462-2469.

[9] 陳萍, 唐任遠, 佟文明, 等. 高功率密度永磁同步電機永磁體渦流損耗分布規(guī)律及其影響[J]. 電工技術學報, 2015, 30(6): 1-9.

Chen Ping, Tang Renyuan, Tong Wenming, et al. Permanent magnet eddy current loss and its influence of high power density permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 1-9.

[10] Takahashi I, Koganezawa T, Su Guijia, et al. A super high speed PM motor drive system by a quasi-current source inverter[J]. IEEE Transactions on Industry Applications, 1994, 30(3): 683-690.

[11] Cho H W, Jang S M, Choi S K. A design approach to reduce rotor losses in high-speed permanent magnet machine for turbo-compressor[J]. IEEE Transactions on Magnetics, 2006, 42(10): 3521-3523.

[12] Zhou Fengzheng, Shen Jianxin, Fei Weizhong, et al. Study of retaining sleeve and conductive shield and their influence on rotor loss in high-speed PM BLDC motors[J]. IEEE Transactions on Magnetics, 2006, 42(10): 3398-3400.

[13] Yamazaki K, Fukushima Y. Effect of eddy-current loss reduction by magnet segmentation in synchronous motors with concentrated windings[J]. IEEE Transa- ctions on Industry Applications, 2011, 47(2): 779- 788.

[14] 孫權貴, 鄧智泉, 張忠明. 基于齒槽效應的高速永磁電機轉子渦流損耗解析計算[J]. 電工技術學報, 2018, 33(9): 1994-2004.

Sun Quangui, Deng Zhiquan, Zhang Zhongming. Analytical calculation of rotor eddy current losses in high speed permanent magnet machines accounting for influence of slot opening[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1994- 2004.

[15] 張超, 陳麗香, 于慎波, 等. 不同保護型式下的高速表貼式永磁轉子應力與溫升分析[J]. 電工技術學報, 2019, 34(9): 1815-1824.

Zhang Chao, Chen Lixiang, Yu Shenbo, et al. Stress and temperature rise of high speed surface-mounted permanent magnet rotor with different protection types[J]. Transactions of China Electrotechnical Society, 2019, 34(9): 1815-1824.

[16] 朱龍飛, 祝天利, 于慎波, 等. 一種氣隙磁導諧波引起的永磁體渦流損耗的解析計算方法[J]. 電工技術學報, 2020, 24(5): 10-16.

Zhu Longfei, Zhu Tianli, Yu Shenbo, et al. Analytical approach for calculation of eddy current losses in magnets caused by permeance harmonics in air gap[J]. Transactions of China Electrotechnical Society, 2020, 24(5): 10-16.

[17] Sun Afang, Li Jian, Qu Ronghai, et al. Effect of multilayer windings on rotor losses of interior permanent magnet generator with fractional-slot concentrated windings[J]. IEEE Transactions on Magnetics, 2014, 50(11): 1-4.

[18] Dajaku G, Gerling D. Low costs and high-efficiency electric machines[C]//2nd International Electric Drives Production Conference, Nuremberg, Germany, 2013: 1-7.

[19] Dajaku G, Xie Wei, Gerling D. Reduction of low space harmonics for the fractional slot concentrated windings using a novel stator design[J]. IEEE Transa- ctions on Magnetics, 2014, 50(5): 1-12.

[20] 徐廣人, 唐任遠, 安忠良. 永磁同步電動機氣隙磁場分析[J]. 沈陽電力高等專科學校學報, 2001, 3(2): 1-4.

Xu Guangren, Tang Renyuan, An Zhongliang. The analysis of airgap magnetic field of permanent magnet synchronous motor[J]. Journal of Shenyang Electric Power Institute, 2001, 3(2): 1-4.

Design and Analysis of Double-Sided Dislocated High Speed Permanent Magnet Linear Synchronous Motors

（School of Electrical Engineering and Automation Harbin Institute of Technology Harbin 150001 China）

As for the traditional 4-pole 6-slot double-sided symmetrical long primary permanent magnet linear synchronous motor, under the condition of ensuring the electromagnetic thrust, an effective method to reduce the permanent magnet eddy current loss was proposed by adopting bilateral dislocation. The basic structure of the motor was introduced. The double-sided dislocation structure could completely eliminate the even number of armature harmonic magnetomotive force, thereby greatly reducing the permanent magnet eddy current loss. The finite element analysis (FEA) software was adopted to analyze the detent forces of symmetric and dislocation structures, the electromagnetic thrust and the secondary eddy current losses. The accuracy of the dislocation method was proved and the structure was optimized. At last, a prototype was developed, and its back-electromotive force (back-EMF), detent force and static thrust were measured through an experimental platform.

Double-sided dislocation, permanent magnet linear synchronous motor, fractional-slot concentrated-windings, permanent magnet eddy current loss

TM359.4

10.19595/j.cnki.1000-6753.tces.200802

國家自然科學基金（51520105010）國際（地區(qū)）合作與交流資助項目。

2020-07-07

2020-11-30

寇寶泉 男，1968年生，教授，博士生導師，研究方向為特種電機及其驅動控制技術。E-mail: koubq@hit.edu.cn（通信作者）

葛慶穩(wěn) 男，1990年生，博士研究生，研究方向為新型永磁直線電機及其優(yōu)化設計。E-mail: 17B906010@stu.hit.edu.cn

（編輯 崔文靜）