基于遞歸徑向基神經網絡的永磁直線同步電機智能二階滑模控制
王天鶴 趙希梅 金鴻雁
基于遞歸徑向基神經網絡的永磁直線同步電機智能二階滑模控制
王天鶴 趙希梅 金鴻雁
(沈陽工業大學電氣工程學院 沈陽 110870)
針對永磁直線同步電機(PMLSM)易受系統參數變化、外部擾動、摩擦力等不確定性因素影響的問題,采用二階滑模控制(2OSMC)和遞歸徑向基神經網絡(RRBFNN)相結合的智能二階滑模控制(I2OSMC)方法來提高系統控制性能。利用2OSMC削弱傳統滑模控制中的抖振問題,提高了系統的位置跟蹤精度。但由于難以估計系統中不確定性因素的邊界,從而無法實現2OSMC的最佳性能,因此,引入RRBFNN對不確定性因素進行估計。由于RRBFNN具有較快的學習能力,可通過在線訓練網絡參數,進而提高系統的魯棒性。實驗結果表明,所提出的控制方法切實可行,能夠有效地抑制不確定性因素對系統的影響,使系統具有較高的位置跟蹤精度和較強的魯棒性能。
永磁直線同步電機 不確定性因素 二階滑模控制 遞歸徑向基神經網絡
0 引言
近年來,隨著電力電子技術的進步以及高性能永磁材料的發展,永磁直線同步電機(Permanent Magnet Linear Synchronous Motor, PMLSM)受到了極大的重視[1]。由于具有結構簡單、沒有機械摩擦力、推力大和體積小等優點,PMLSM適合于高性能伺服應用場合,廣泛應用于交通運輸、航空航天、工業與自動化、儀器儀表和軍工業等領域[2]。PMLSM的特點在于利用電能直接產生直線運動,不需要中間轉換結構,省去了傳動鏈、齒輪組、滾珠絲杠等間接機械傳動裝置,消除了間隙死區、摩擦以及彈性等影響,但同時PMLSM伺服系統性能受時變不確定性因素影響很大,其中包括系統參數變化、外部擾動、摩擦力等[3-4]。因此,為降低不確定性因素對系統的影響,必須設計出適合的控制器,使系統具有強魯棒性,從而提高系統控制性能。
為此,近年來,國內外學者對電機控制方法進行了廣泛的研究,并提出了魯棒控制、模糊控制、神經網絡控制和滑模控制等多種控制方法[5]。其中滑模控制能夠克服系統的不確定性因素,對擾動具有很強的魯棒性,尤其對非線性系統的控制具有良好的控制效果,因此,在電機控制方面得到了廣泛的應用[6]。但由于在接近滑模面時的慣性或延遲等原因,致使滑模控制存在抖振問題。為此,提出了將魯棒控制、神經網絡控制、模糊控制等與滑模控制相結合的混合控制策略以抑制抖振現象[7]。文獻[8]采用積分滑模控制方法,提高了系統的響應速度,同時減小了穩態誤差,但當系統狀態偏出給定軌跡時將導致系統不穩定。文獻[9]提出一種結合滑模觀測器和模糊控制各自優點的模糊滑模速度位置估計方法,保證了系統的魯棒性和控制精度,但是模糊控制器的模糊規則選取需要依靠大量經驗。文獻[10]設計了二階滑模控制器,該方法充分利用了輔助滑模面,在不增加復雜度的前提下,有效抑制抖振,提高系統的位置跟蹤性能。但其難以估計不確定性因素的邊界,因此,將模型參考自適應估計器與二階滑模控制器相結合,從而提高系統的魯棒性。由此可知,系統不確定性因素的邊界難以預測,也為滑模控制器的設計以及抖振的抑制增加了難度[11]。為此,文獻[12]提出將Elman神經網絡與互補滑模控制相結合的方法,利用Elman神經網絡對不確定性因素的邊界進行估計,但在Elman網絡模型中只計入了隱層節點的反饋,而沒有考慮輸出層節點的反饋,從而影響了網絡的收斂速度和精度。文獻[13-14]提出將徑向基神經網絡(Radial Basis Function Neural Network, RBFNN)分別與滑模控制和快速終端滑模控制相結合的方法,利用RBFNN對不確定性因素的邊界進行實時估計,從而改善系統的性能,但其網絡結構固定且學習速度較慢。
為解決不確定性因素對PMLSM伺服系統的影響,使系統具有良好的位置跟蹤精度及強魯棒性,本文提出基于遞歸徑向基神經網絡(Recurrent Radial Basis Function Neural Network, RRBFNN)的智能二階滑模控制(Intelligent Second-Order Sliding Mode Control, I2OSMC)方法。二階滑模控制(Second-Order Sliding Mode Control, 2OSMC)采用飽和函數替換傳統切換函數,削弱了抖振現象,并抑制系統不確定性因素對系統的影響。但由于不確定性因素的邊界在實際應用中很難提前獲知,因此結合RRBFNN的學習能力強和2OSMC魯棒性強的優點設計I2OSMC方法,RRBFNN可以在線調節神經網絡參數,從而有效地估計并抑制不確定性因素,保證系統的強魯棒性。最后,通過基于數字信號處理器(Digital Signal Processor, DSP)的實驗平臺對PMLSM伺服系統進行實驗驗證,結果表明,所提出的方法具有良好的控制性能。
1 PMLSM數學模型
在同步參考坐標系下,PMLSM的電壓方程和磁鏈方程表示為
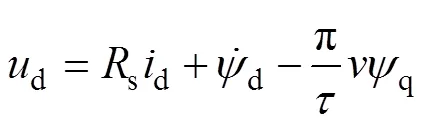
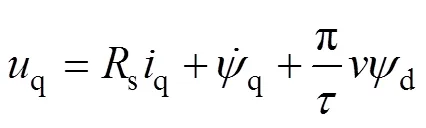
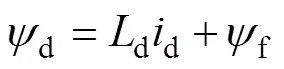
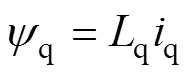
電磁推力方程表示為
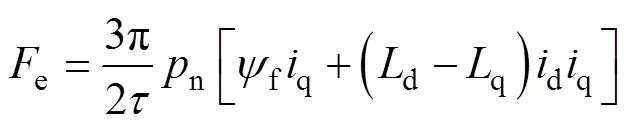
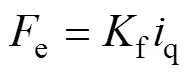
PMLSM運動方程可表示為
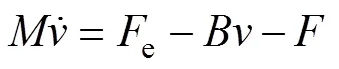
若忽略系統參數變化、外部擾動和摩擦力等不確定性因素對PMLSM伺服系統的影響,可將式(7)改寫成理想狀態下的動態方程為
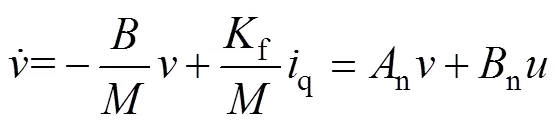
其中,系統控制輸入為
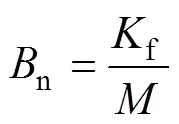
若考慮不確定性因素對系統的影響,式(7)可改寫為
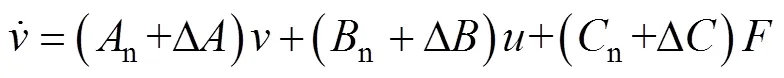
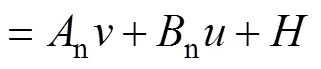
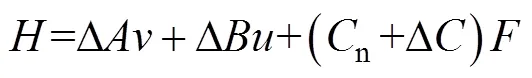
其中
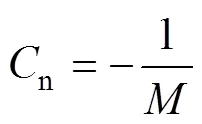
2 PMLSM控制系統設計
2.1 PMLSM系統組成
PMLSM的智能二階滑模控制系統框圖如圖1所示。其中,點畫線框內為智能二階滑模控制器。控制系統主要由智能二階滑模控制器、PI控制器、坐標變換、電機檢測單元等組成。I2OSMC采用2OSMC與RRBFNN相結合的方法來設計,能夠有效估計并抑制系統不確定性因素。
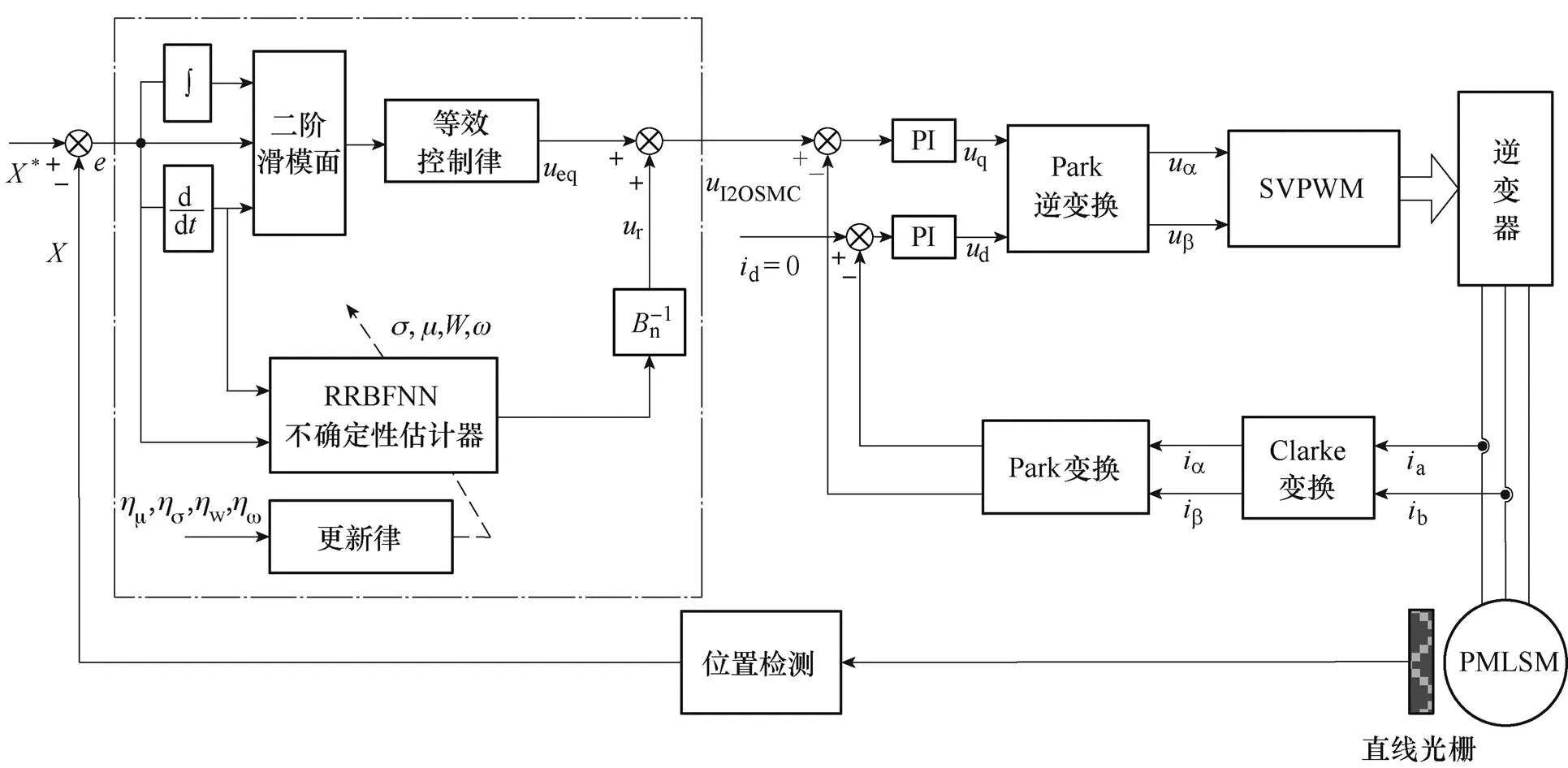
圖1 PMLSM的智能二階滑模控制系統框圖
2.2 二階滑模控制器設計
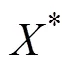
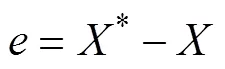
為消除由不確定性因素的存在所產生的穩態誤差,引入積分項,因此定義滑模變量及其導數為
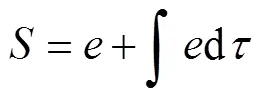
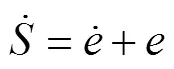
設計二階滑模面為
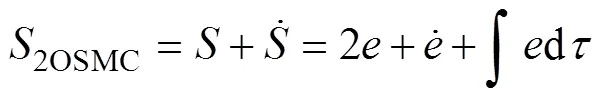
由式(14)可以看出,二階滑模面是一種比例-積分-微分型滑模面,這種設計既可以實現積分項消除系統跟蹤的穩態誤差的優點,又可以避免系統響應延遲的缺點。
將式(9)代入式(14)并對其求導得
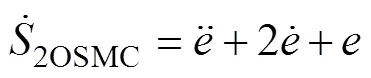
為保證系統的穩定性,設計2OSMC的控制律,其由等效控制律和切換控制律組成,表示為
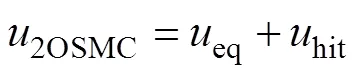
選擇李雅普諾夫函數為
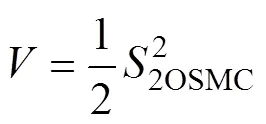
對求導,并將式(14)~式(16)代入可得
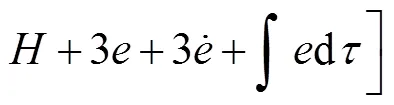
因此,設計等效控制律為
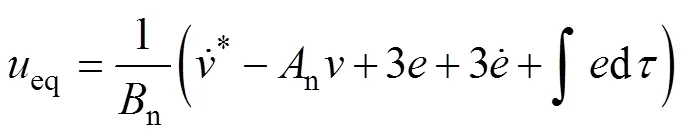
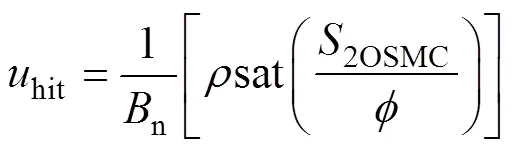
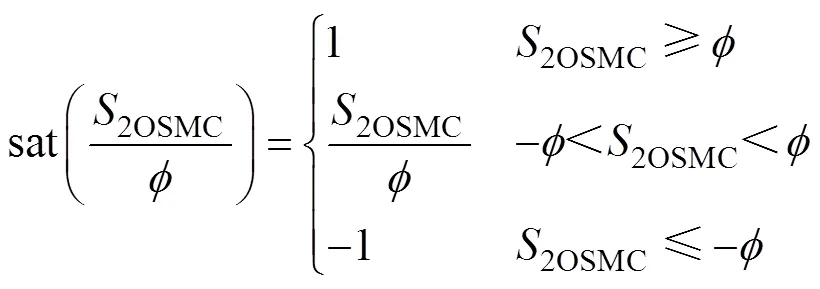
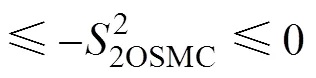
由式(22)可知,系統滿足李雅普諾夫漸近穩定條件,這確保了系統狀態軌跡將在有限時間內到達滑模面。2OSMC結構框圖如圖2所示。
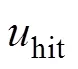
2.3 RRBFNN不確定性估計器
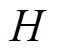
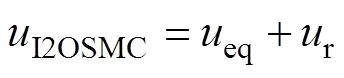
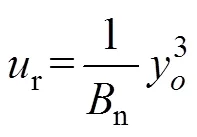
2.3.1 RRBFNN的網絡結構
為了提高函數逼近的精度,本文采用了三層RRBFNN結構,如圖3所示,包括輸入層(I層)、隱含層(J層)和輸出層(O層)。同時,由于其連續和微分特性,采用高斯函數作為隱含層中節點的激活函數。此外,RRBFNN的輸出通過時間延遲遞歸到輸入層以增強網絡的動態學習能力。
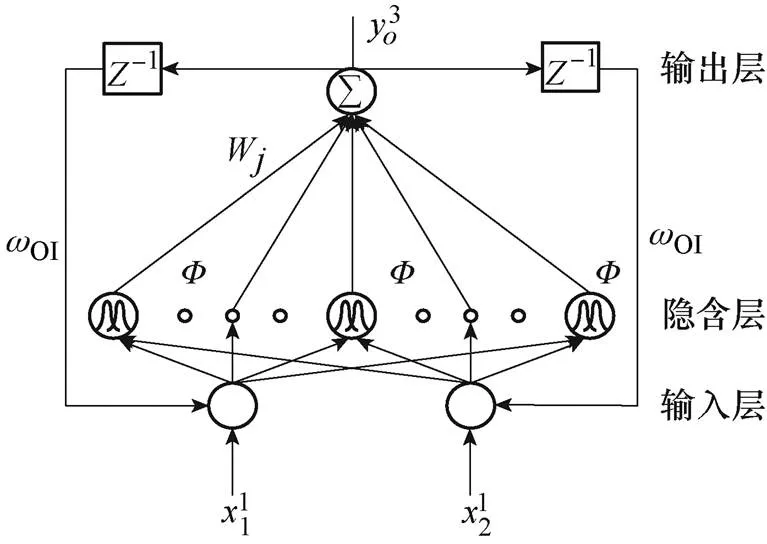
圖3 RRBFNN結構
RRBFNN各層的信號傳播和基本功能如下:
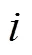

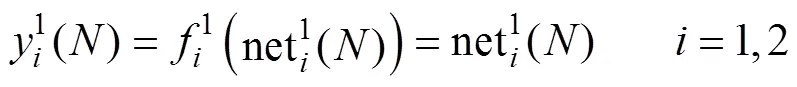

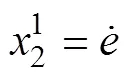
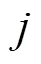
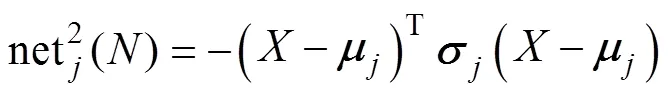
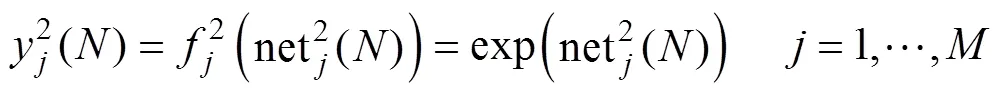
(3)輸出層。RRBFNN的輸出表示為
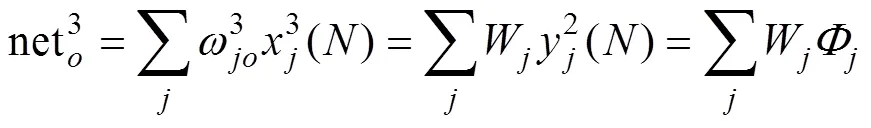
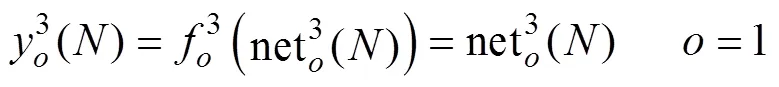
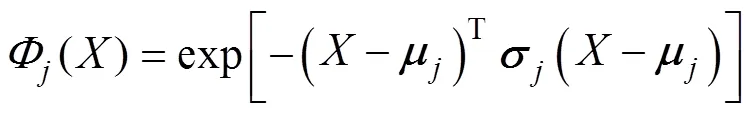
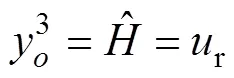
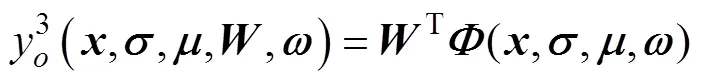
2.3.2 RRBFNN在線學習算法
在RRBFNN中,連接權值的修正可以采用反向傳播算法。定義能量函數為
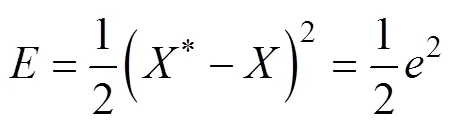
RRBFNN的參數更新律如下:
在輸出層中,要傳播的誤差項為
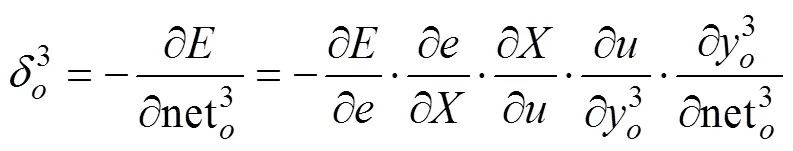
權重的數值更新為
(38)
輸出層的權重更新為
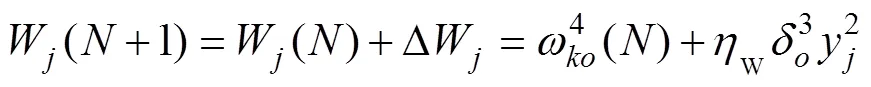
在隱含層中,要傳播的誤差項為
(40)
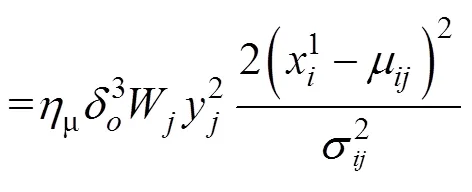
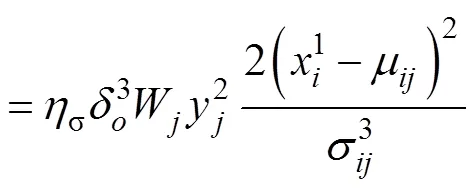
平均值和標準差更新律為
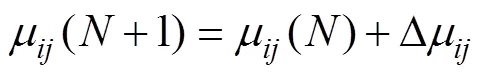
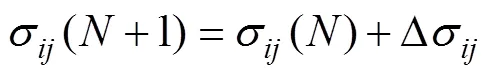
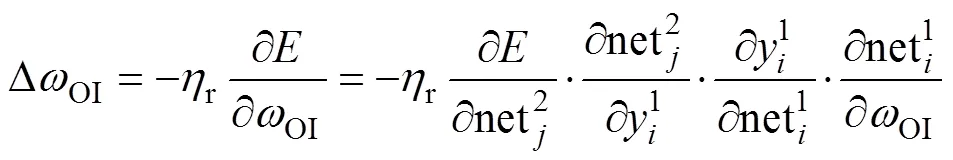
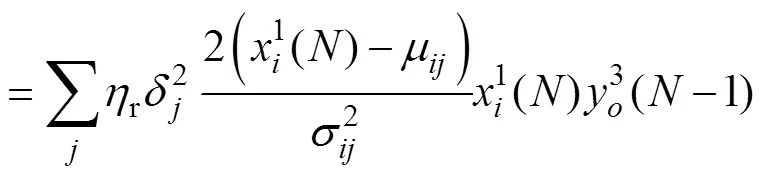
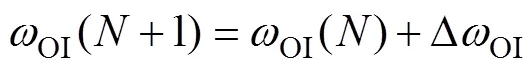
3 系統實驗分析
實驗采用的PMLSM生產于美國Kollmorgen公司,PMLSM伺服系統的核心控制單元為TI公司推出的DSP TMS320F28335。PMLSM控制系統結構如圖4所示,其硬件結構可分為運算控制單元、供電電路、檢測單元和PMLSM。運算控制單元為PC和DSP;PMLSM的供電電路由整流器和逆變器組成,逆變器開關頻率為5kHz;檢測電路包括電壓、電流、速度和位置信號的檢測,位置信號的檢測采用直線光柵傳感器,其精度為1mm。實驗中將采用2OSMC、基于RBFNN的2OSMC和基于RRBFNN的I2OSMC三種方法,通過實驗對比分析證明I2OSMC方法的可行性。
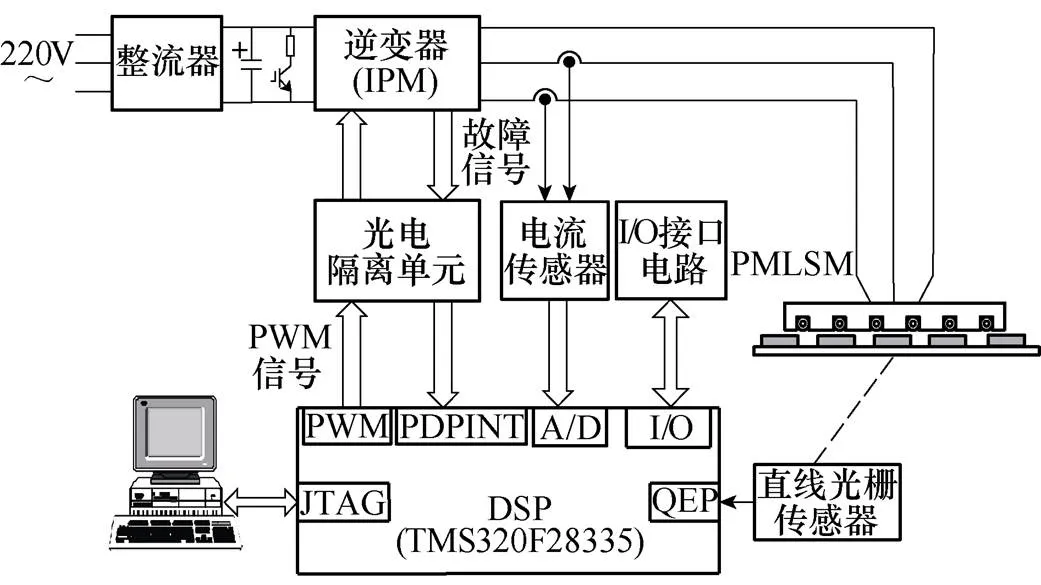
圖4 基于DSP的PMLSM控制系統結構
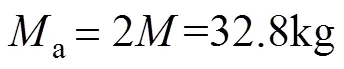
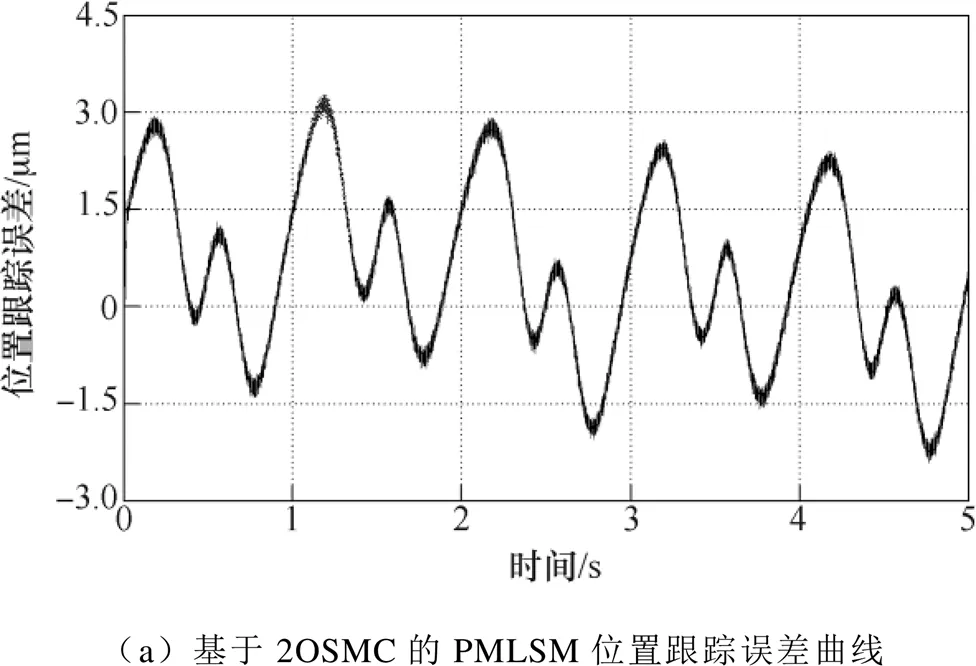
為驗證所提出的I2OSMC在負載擾動存在時的控制性能,對系統給定如圖6所示的梯形輸入信號,并在2.5s時對系統突加50N負載。為更好地實現與傳統控制的對比,本實驗采用了傳統PI控制與其他三種控制方法進行對比。采用傳統PI控制、2OSMC、基于RBFNN的2OSMC和基于RRBFNN的I2OSMC方法的位置跟蹤誤差曲線如圖7所示。為方便對比,給出四種控制方法下位置跟蹤誤差的最大值、平均值以及標準差三種度量來進行比較,誤差大小對比見表1。對比圖7b和圖7c可以看出,將神經網絡與2OSMC相結合能夠有效地減小位置跟蹤誤差并削弱抖振,但由于RBFNN為靜態神經網絡,其學習能力稍慢,致使系統響應速度略有下降。對比圖7d和圖7b可看出,I2OSMC具有更好的位置跟蹤精度,其動態響應能力與2OSMC相近,但明顯快于基于RBFNN的2OSMC方法。因此,將I2OSMC應用于PMLSM伺服系統有效可行,對于提高系統位置跟蹤精度和魯棒性能具有重要的意義。
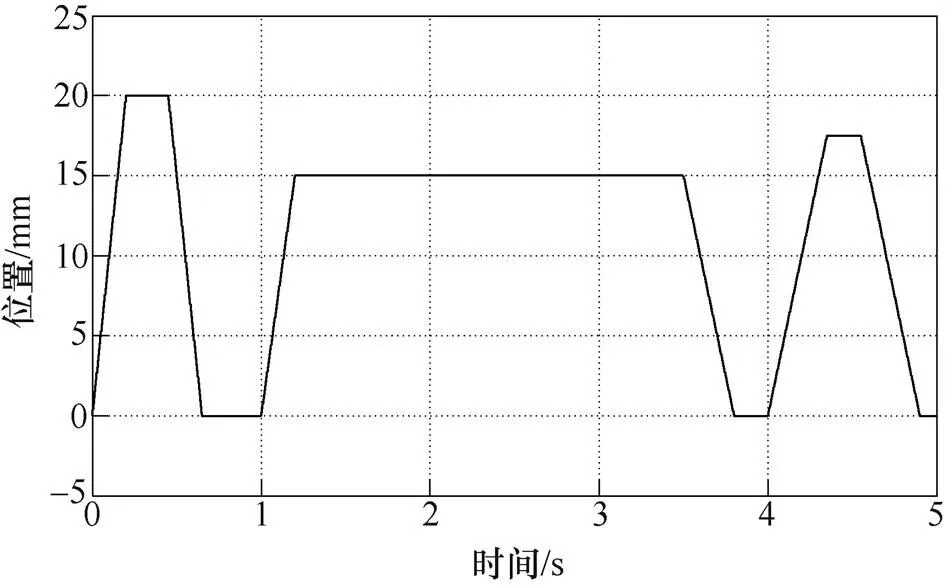
圖6 梯形輸入信號
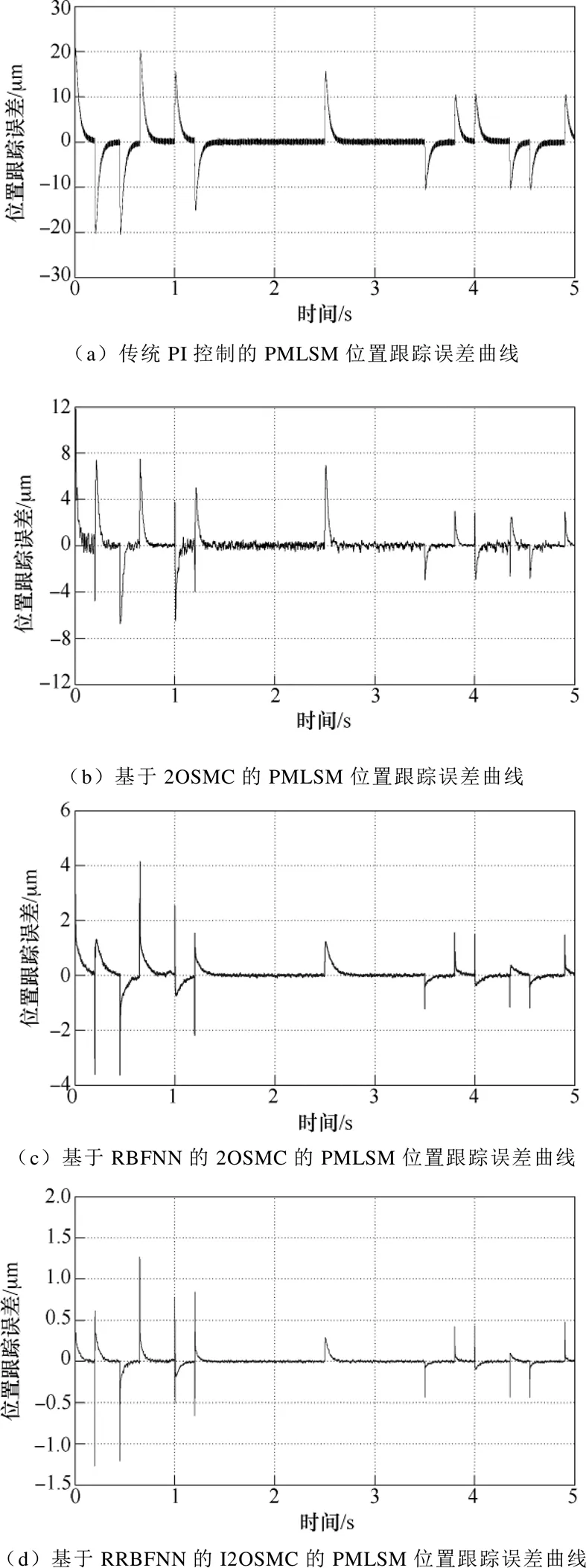
圖7 梯形信號下的位置誤差曲線
表1 位置跟蹤誤差對比
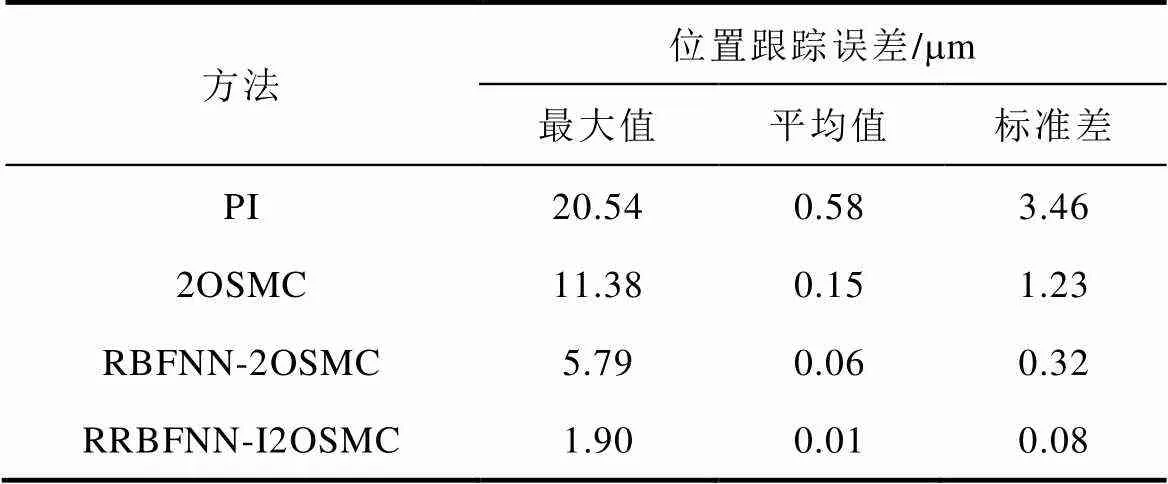
Tab.1 Comparison of position tracking errors
4 結論
本文采用基于RRBFNN的I2OSMC的位置控制方法來抑制系統不確定性因素的影響。在I2OSMC設計中,2OSMC用來削弱抖振、提高系統魯棒性;RRBFNN旨在估計并抑制系統的不確定性因素邊界。實驗結果表明,同2OSMC方法和基于RBFNN的2OSMC方法相比,I2OSMC既具有快速準確的位置跟蹤性能,又具有較強的抗干擾能力,對PMLSM伺服系統有更好的控制效果。
[1] Kazraji S M, Soflayi R B, Sharifian M B B. Sliding-mode observer for speed and position sensor- less control of linear-PMSM[J]. Electrical Control & Communication Engineering, 2014, 5(1): 20-26.
[2] 智淑亞, 吳洪兵. 數控進給伺服系統摩擦補償控制仿真[J]. 沈陽工業大學學報, 2019, 41(4): 361-365.
Zhi Shuya, Wu Hongbing. Simulation of friction compensation control of NC feed servo system[J]. Journal of Shenyang University of Technology, 2019, 41(4): 361-365.
[3] Chen S Y, Liu T S. Intelligent tracking control of a PMLSM using self-evolving probabilistic fuzzy neural network[J]. IET Electric Power Applications, 2017, 11(6): 1043-1054.
[4] 朱國昕, 雷鳴凱, 趙希梅. 永磁同步電機伺服系統自適應迭代學習控制[J]. 沈陽工業大學學報, 2018, 40(1): 6-11.
Zhu Guoxin, Lei Mingkai, Zhao Ximei. Adaptive iterative learning control for permanent magnet synchronous motor servo system[J]. Journal of Shenyang University of Technology, 2018, 40(1): 6-11.
[5] 孟高軍, 袁野, 孫玉坤, 等. 帶定位力補償的擴張觀測器磁通切換永磁直線電機無位置傳感器控制策略[J]. 電工技術學報, 2018, 33(17): 4091-4101.
Meng Gaojun, Yuan Ye, Sun Yukun, et al. Extended state observer with cogging force compensation for sensorless control strategy of linear flux-switching permanent magnet machine[J]. Transaction of China Electrotechnical Society, 2018, 33(17): 4091-4101.
[6] Namazi M M, Rashidi A, Saghaian-Nejad S M, et al. Chattering-free robust adaptive sliding-mode control for switched reluctance motor drive[C]//IEEE Trans- portation Electrification Conference and Expo, Michigan, USA, 2016: 474-478.
[7] 劉金琨, 孫富春. 滑模變結構控制理論及其算法研究與進展[J]. 控制理論與應用, 2016, 24(3): 407- 418.
Liu Jinkun, Sun Fuchun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory and Applications, 2016, 24(3): 407- 418.
[8] 侯勇, 趙姍姍, 王勇. 永磁同步電機的積分型滑模變結構控制[J]. 天津科技大學學報, 2013, 28(2): 55-58.
Hou Yong, Zhao Shanshan, Wang Yong. Integral sliding mode variable structure control of permanent magnet synchronous motor[J]. Journal of Tianjing University of Science and Technology, 2013, 28(2): 55-58.
[9] 陸華才, 提娟, 劉怡君, 等. 基于模糊滑模觀測器的PMLSM無傳感器控制[J]. 信息與控制, 2016, 45(1): 60-65.
Lu Huacai, Ti Juan, Liu Yijun, et al. Sensorless control of PMLSM based on fuzzy sliding mode observer[J]. Information and Control, 2016, 45(1): 60-65.
[10] Zhao Lihang, Huang Jin, Liu He, et al. Second-order sliding-mode observer with online parameter identi- fication for sensorless induction motor drives[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10): 5280-5289.
[11] Panah P G, Ataei M, Mirzaeian B, et al. A robust adaptive sliding mode control for PMLSM with variable velocity profile over wide range[J]. Research Journal of Applied Sciences Engineering & Tech- nology, 2015, 10(9): 997-1006.
[12] 趙希梅, 金鴻雁. 基于Elman神經網絡的永磁直線同步電機互補滑模控制[J]. 電工技術學報, 2018, 33(5): 973-979.
Zhao Ximei, Jin Hongyan. Complementary sliding mode control for permanent magnet linear synchronous motor based on Elman neural network[J]. Transaction of China Electrotechnical Society, 2018, 33(5): 973-979.
[13] 朱玲, 李艷東, 孫明, 等. 移動機器人編隊的神經網絡滑模控制[J]. 電機與控制學報, 2014, 18(3): 113-118.
Zhu Ling, Li Yandong, Sun Ming, et al. Sliding mode control of mobile robot formations based on neural networks[J]. Electric Machines and Control, 2014, 18(3): 113-118.
[14] Qi Liang, Shi Hongbo. Adaptive position tracking control of permanent magnet synchronous motor based on RBF fast terminal sliding mode control[J]. Neurocomputing, 2013, 115: 23-30.
[15] 朱煜峰, 許永鵬, 陳孝信, 等. 基于卷積神經網絡的直流XLPE電纜局部放電模式識別技術[J]. 電工技術學報, 2020, 35(3): 211-220.
Zhu Yufeng, Xu Yongpeng, Chen Xiaoxin, et al. Pattern recognition of partial discharges in DC XLPE cables based on convolutional neural network[J]. Transaction of China Electrotechnical Society, 2020, 35(3): 211-220.
[16] Xia Meizhen, Zhang Tianping. Adaptive neural network control for stochastic constrained block structure nonlinear systems with dynamical uncertainties[J]. International Journal of Adaptive Control and Signal Processing, 2019, 33(11): 1079-1096.
[17] An Ru, Li Wenjing, Han Honggui, et al. An improved Levenberg-Marquardt algorithm with adaptive learning rate for RBF neural network[C]//35th Chinese Con- trol Conference, Chengdu, 2016: 3630-3635.
Intelligent Second-Order Sliding Mode Control Based on Recurrent Radial Basis Function Neural Network for Permanent Magnet Linear Synchronous Motor
(School of Electrical Engineering Shenyang University of Technology Shenyang 110870 China)
The permanent magnet linear synchronous motor (PMLSM) is susceptible to uncertainty factors, such as system parameter variation, external disturbance and friction. Thus, an intelligent second-order sliding mode control (I2OSMC) method combining second-order sliding mode control (2OSMC) and recurrent radial basis function neural network (RRBFNN) is used to improve system control performance. The design of 2OSMC weakens the chattering problem in the traditional sliding mode control and improves the position tracking accuracy of the system. However, because it is difficult to estimate the boundary of the uncertainty factors in the system, the optimal performance of 2OSMC cannot be achieved. Therefore, the RRBFNN is introduced to improve the robustness of the system, which has faster learning ability and can train the network parameters online. The experimental results show that the proposed control method is feasible and can effectively suppress the influence of uncertainty factors on the control system, so that the system has higher position tracking accuracy and stronger robust performance.
Permanent magnet linear synchronous motor, uncertainty factors, second-order sliding mode control, recurrent radial basis function neural network
TM351; TP273
10.19595/j.cnki.1000-6753.tces.191238
遼寧省自然科學基金計劃重點資助項目(20170540677)。
2019-09-24
2019-11-26
王天鶴 男,1993年生,碩士研究生,研究方向為電機控制、智能控制等。E-mail: wangtianhech@163.com
趙希梅 女,1979年生,教授,博士生導師,研究方向為電機控制、魯棒控制等。E-mail: zhaoxm_sut@163.com(通信作者)
(編輯 崔文靜)

