基于離散趨近律與無差拍雙閉環結構的單相LCL型PWM整流器控制策略

李景灝 吳愛國

基于離散趨近律與無差拍雙閉環結構的單相LCL型PWM整流器控制策略

李景灝 吳愛國

（天津大學電氣自動化與信息工程學院 天津 300072）

對于單相LCL型PWM整流器，傳統雙閉環控制以PI控制為電壓外環，電流內環常采用以變換器側電流為受控量的無差拍控制。該方案存在兩個問題：①電壓外環的積分器會限制系統動態性能；②無法精確實現網側單位功率因數。為此，該文提出一種以離散趨近律控制為電壓外環、以改進無差拍控制為電流內環的雙閉環控制策略。對于電壓外環，該文推導網側半波電流峰值與該半波周期內直流側電壓增量之間的數學關系，在此基礎上提出一種離散趨近律控制策略。對于電流內環，提出一種以網側電流和變換器側電流的加權和為受控量的改進無差拍算法，并給出實現精確單位功率因數所需的電流參考值。該文還討論網側電流欠阻尼振蕩引起的電流過沖問題，并提出解決方法。仿真和實驗結果表明，所提雙閉環控制顯著改善了系統動態性能，且實現了精確網側單位功率因數。

單相PWM整流器 LCL型濾波器 離散趨近律 無差拍控制 欠阻尼振蕩

0 引言

與傳統的不控整流器和相控整流器相比，PWM整流器具有網側接近單位功率因數、諧波注入少、可實現能量流動的雙向控制等優點，已經廣泛應用于不間斷電源、鐵路功率調節器、光伏發電等領域。在一些應用場合，對PWM整流器的動態性能有較高要求。為此，已有不少文獻對PWM整流器的先進控制算法進行了研究，以期在不改變主電路參數設計的情況下實現系統動態性能的改善。

對于單相PWM整流器，通常采用電壓、電流雙閉環控制。一種思路是令電壓外環采用PI控制器產生參考電流幅值，將該值與電網電壓鎖相信號相乘后得到電流內環的交流參考信號，并采用PR控制器對該交流信號實現無穩態誤差跟蹤。基于這種思路，文獻[1]研究了在離散域中直接進行電流環PR控制器設計的方法。文獻[2]基于Lyapunov方法分析了采用PR控制時單相PWM變換器非線性動態過程的穩定性，并提出了控制器參數的整定原則。這種控制思路雖然有效，但難以實現有功、無功功率的解耦控制。另一種思路是采用類似于三相PWM整流器的基于旋轉坐標變換的有功、無功功率解耦控制方法。通過引入虛擬正交量，可將單相整流器模型變換為兩相正交的交流系統，進而像三相PWM整流器一樣實現有功、無功的解耦控制。基于這一思路，文獻[3]推導了旋轉坐標系下的電流環解耦數學模型，設計了∞控制器，提高了電流環動態性能和系統魯棒性。文獻[4]提出了一種基于二階數字有限長單位沖激響應（Finite Impulse Response, FIR）陷波器和功率前饋方案的改進控制策略，提高了系統動態性能。考慮到引入虛擬變量的過程會產生1/4電網周期的控制延遲，導致系統穩定性和動態性能的下降。文獻[5]利用變換器參數直接構造了虛擬正交量，避免了控制延遲的產生。文獻[6]提出了一種任意相位延時算法，理論上可將控制延遲縮短至一個采樣周期，但需要考慮抗干擾問題。為了進一步提高系統動態性能，一些文獻將無差拍和模型預測控制方法引入到單相PWM整流器控制中。文獻[7]提出了一種改進的無差拍電流預測控制方法，避免了控制延時導致的電流畸變。文獻[8]提出了一種基于牛頓插值的功率前饋無差拍控制算法，改善了動態響應和電流預測精度。文獻[9]提出了一種基于最小電流誤差的模型預測電流控制，改善了動態響應并實現了零穩態誤差。文獻[10]提出了一種包含積分補償環節的模型預測控制。文獻[11]提出了一種基于調制電壓矢量優化的定頻模型預測電流控制。這些方法不同程度地改善了單相PWM整流器的穩態和動態性能。上述研究都是針對單相L型變換器討論的。對于單相LCL型變換器，文獻[12]利用擴張狀態觀測器推導了一種僅需檢測網側電流的電流環解耦控制策略。文獻[13]研究了僅采用網側電流反饋實現功率控制與有源阻尼的參數優化方法。文獻[14]提出了一種利用網側電流高頻分量反饋實現有源阻尼的方法。文獻[15-17]討論了基于LCL型濾波的三相變流器的電流控制策略，其結果可為單相LCL型整流器的控制提供借鑒。

從現有文獻來看，對于單相PWM整流器的控制，多數文獻僅停留在對電流環的優化上，電壓環仍采用傳統的PI控制。實際上，PI控制器中的積分環節正是制約系統動態性能的主要因素，故有必要從電壓環著手進行控制系統的優化設計。趨近律方法是一種用于設計滑模控制到達過程的方法。作為滑模控制策略的一部分，趨近律方法已經廣泛應用于電力電子領域[18-24]。基于合適的趨近律設計，狀態變量能夠快速到達滑模面，使系統獲得優良的動態性能[25]。為此，本文首先推導了網側半波電流峰值與該半波周期內直流側電壓增量之間的數學關系，并采用離散趨近律方法設計了電壓外環控制器。另一方面，對于單相LCL型整流器，現有的以變換器側電流為受控量的無差拍控制會導致網側偏離單位功率因數。為此，本文提出了一種以網側和變換器側電流的加權和為受控變量的改進無差拍控制，減小了網側功率因數偏差，并進一步推導了實現精確網側單位功率因數所需的電流參考值。通過進一步分析，本文指出了網側電流欠阻尼振蕩可能引起電流過沖的問題，并給出了消除電流過沖的方法。最后，通過仿真和樣機實驗驗證了所提方法在穩態和動態性能方面的優勢。

1 單相LCL型PWM整流器數學模型

單相PWM整流器拓撲如圖1所示。圖1中，交流側濾波器采用了LCL型濾波器，g、分別為網側電感和變換器側電感，g、分別為網側電感和變換器側電感寄生電阻，f為交流側濾波電容，f為無源阻尼電阻，為直流側支撐電容，為負載電阻，S1～S4為功率開關管。

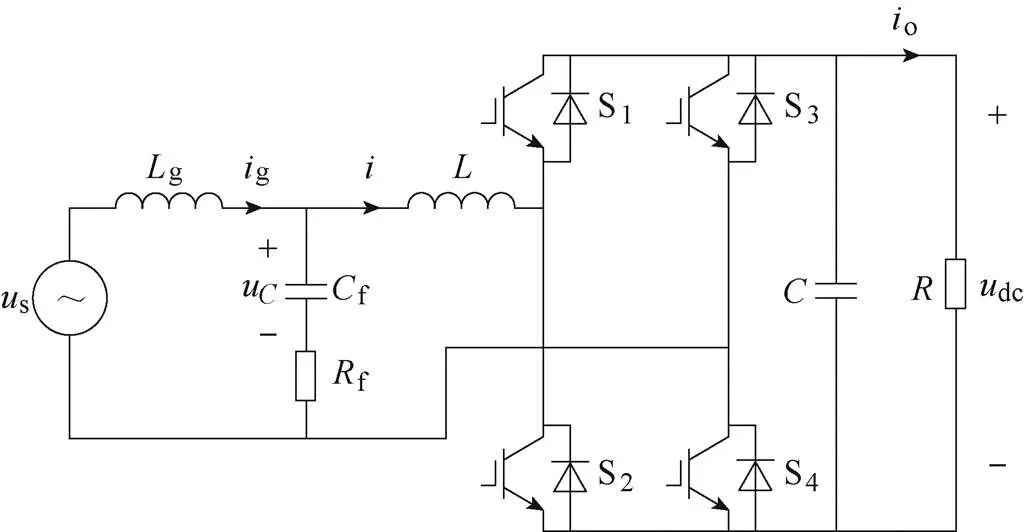
圖1 單相PWM整流器拓撲

根據圖1所示主電路結構，可以得到LCL型整流器的數學模型為

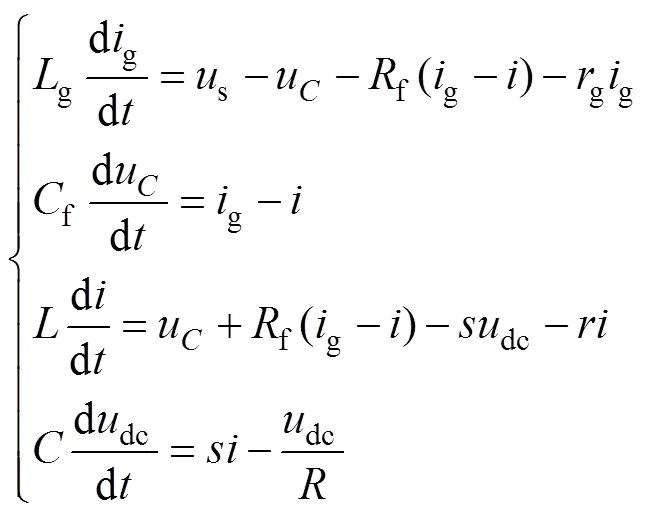
式中，g為網側電流；為變換器側電流；u為交流側濾波電容電壓；s為電網電壓；dc為直流側電壓；為開關函數，其定義為

經過狀態空間平均化處理后，為與電網電壓s同頻率的交流量。

2 基于離散趨近律的電壓外環控制器

本節從電壓外環著手，為了優化單相LCL型PWM整流器的控制性能，提出一種基于離散趨近律的電壓外環控制算法。與傳統的PI控制不同，該算法根據離散趨近律來確定一個半波周期內的參考電流峰值，有利于實現直流側電壓的快速調整。

根據能量守恒定律，在一段時間內由電網發出的能量應等于直流側電容儲能增量、負載消耗能量和寄生電阻損耗、開關管損耗等附加損耗之和。假定網側電流已被控制為和電網電壓同相位，則在一個半波周期內近似的能量平衡關系為

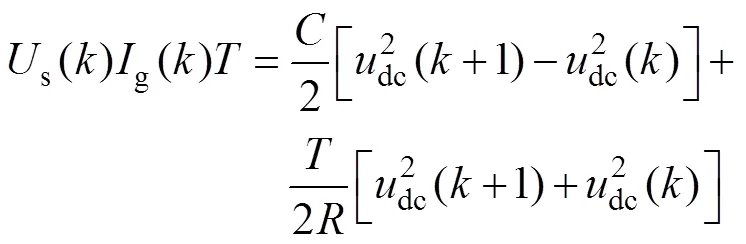
式中，s()、g()分別為第個工頻半波周期（0.01s）電網電壓和網側電流有效值；dc()和dc(+1)分別為第個工頻半波周期起始時刻和終止時刻直流側電容電壓的瞬時值。考慮到系統工況突變時刻（如負載突變）一般不會恰好落在電網電壓過零點處，將定義為：當＞1時，=0.01；當=1時，=0.01-。這里，將突變時刻所在的半波周期定義為“第1個半波周期”，將定義為發生突變時第1個半波周期已經過去的時間。可以看出，從第2個半波周期開始，的取值始終為0.01s。

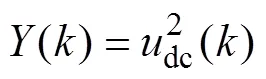
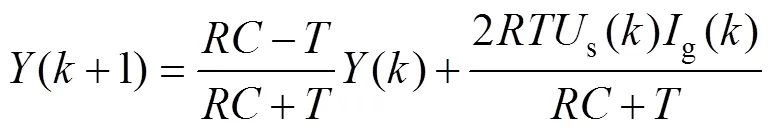
式中，等式右側第二項與g有關，而g是可控的。因此，可將式（4）看作以g為輸入，為輸出的離散時間線性系統。由此，得到了反映單相PWM整流器直流側電壓動態過程的離散化數學模型。該模型形式簡單，且能很好地反映不同峰值的半波交流電流產生的直流側電壓增量。

定義誤差量為

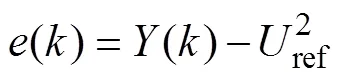
式中，ref為直流側電壓參考值。將式（5）代入式（4），可得

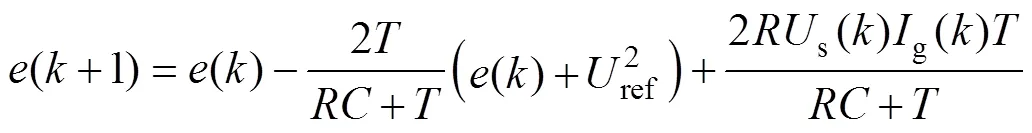
采用如下的離散趨近律，即

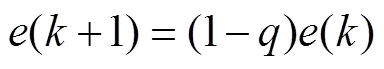
式中，0＜＜1。由壓縮映射原理可知，當()按照式（7）規律變化時，會逐漸趨近于0。

由式（6）、式（7）可求出實現該趨近律所需的網側電流有效值，即

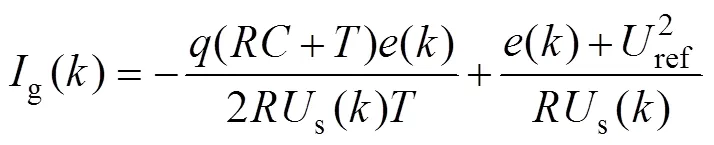
考慮到輸出電壓偏差較大時（如起動過程），可能出現過高的電流參考值[26]，故實際應用趨近律算法時需對電流有效值進行限制，即取

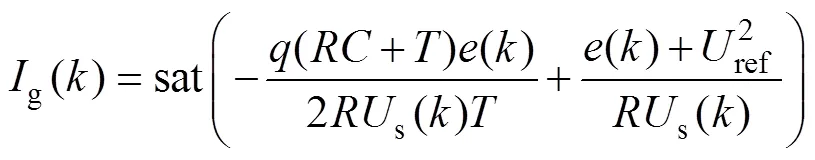
其中

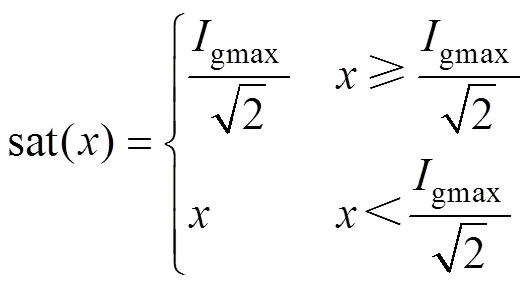
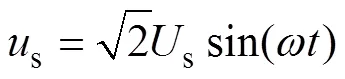
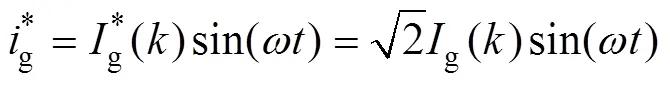
通過合理設計電流內環控制器，即可實現對網側電流參考值的跟蹤控制。第3節將具體闡述電流內環控制策略。

3 改進無差拍控制算法

無差拍控制是一種精確的電流控制算法，具有動態響應快、易于數字實現等優點，常用作單相PWM整流器的電流內環控制算法。該算法的基本思路是根據變換器的數學模型計算被控對象輸入端所需控制量。本節首先指出現有的無差拍控制算法存在的不能實現精確單位功率因數的問題，并提出一種改進的無差拍控制算法。

3.1 改進無差拍控制算法的推導

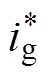
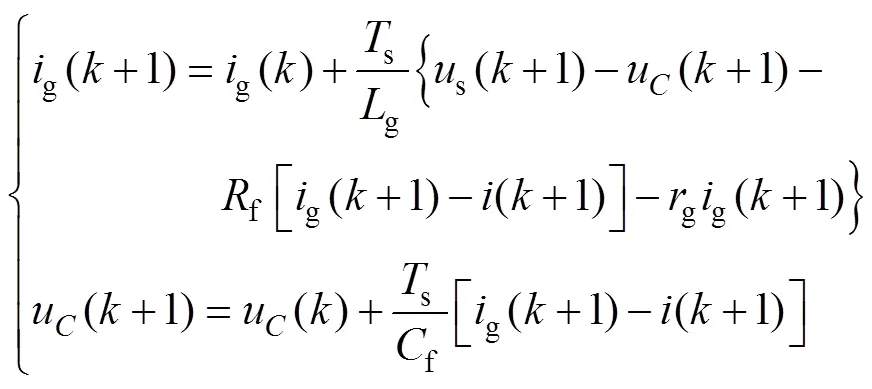
為了實現對網側電流參考值的精確跟蹤，應有g(+1)=()和(+1)=*()。其中，()、*()為時刻的電流參考值。聯立式（11）的兩式，消去u(+1)，可得

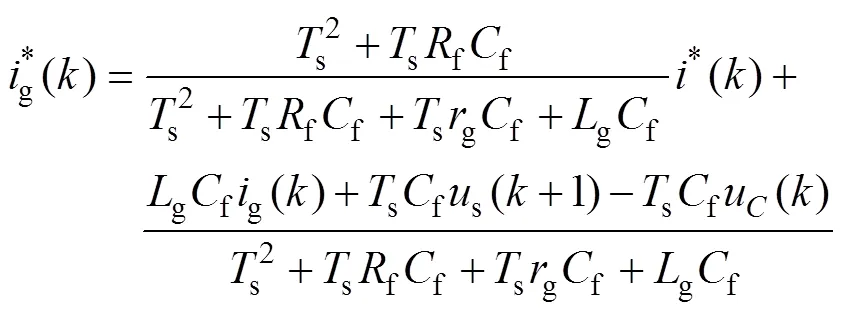
由式（12）可將網側電流參考值轉換為變換器側電流參考值。采用前向差分法對式（1）的第三式進行離散化處理，可得

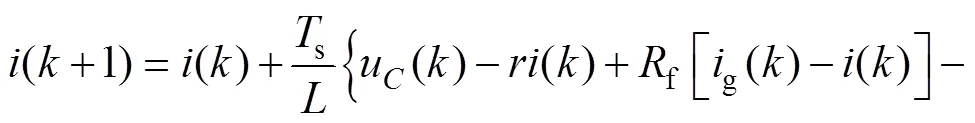
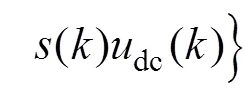
將(+1)=*()代入式（13），可得

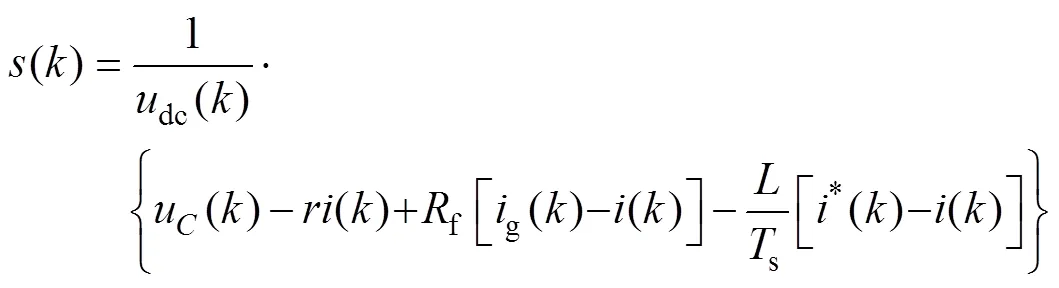
式（12）、式（14）提供了一種精確的單相LCL型整流器網側電流無差拍控制算法。根據該算法，在第個采樣周期[s, (+1)s]的初始時刻獲取u()、()、g()、dc()等變量值和電流參考值*()后，即可根據式（12）、式（14）計算得到控制器作用量，使得第+1個采樣周期的初始時刻的電流值與給定值相等。容易看出，該算法需要同時對g、、u進行采樣，且依賴于所有變換器參數，計算過程比較復雜。

為了避免這種復雜性，考慮到交流側濾波電容f數值很小，文獻[27]采用了一種簡化的無差拍算法（下文稱為“簡化算法”）。該算法忽略了濾波電容電流，即令=*，只使用式（14）作為控制律。與式（12）、式（14）構成的精確算法相比，簡化算法不檢測網側電流g，無需參數f，對系統狀態和參數的依賴較少，且計算量小，易于實現。然而，簡化算法并不能直接控制網側電流，采用該算法會使得網側偏離單位功率因數。另外，簡化算法檢測變量為濾波電容電壓u和變換器側電流，無法直接獲得濾波電容電流值。若要在不增加額外電流傳感器的情況下實現有源阻尼，只能對電容電壓作微分運算，這增加了算法實現的難度。

為了解決上述問題，本文提出一種適用于LCL型整流器的改進無差拍算法。首先，對LCL型整流器的數學模型進行變換，使其在數學模型形式上與L型整流器相似。將式（1）第一式與第三式相加后得

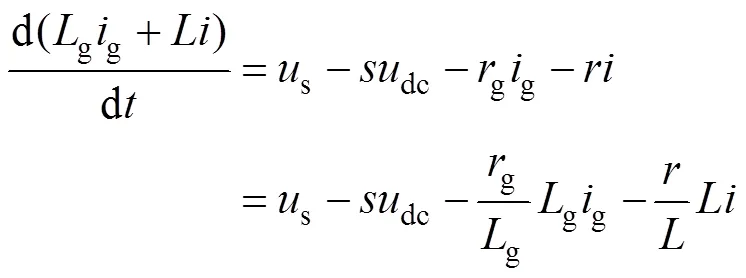
由于電感寄生電阻上的壓降很小，為獲得形式簡單的公式，近似認為

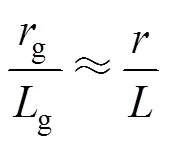
取g=，sum=g+，為網側電感與變換器側電感的比例因子。由此，可將式（1）變換為

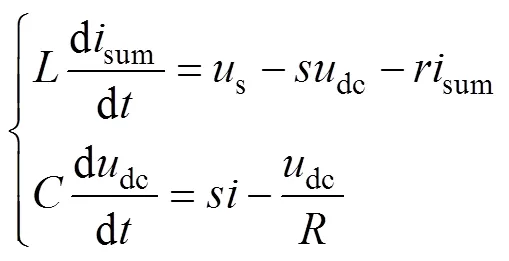
式中，交流側電容電壓作為中間變量被消除。式（17）在形式上與L型整流器的數學模型十分相似。類似于簡化算法思路，暫時忽略交流側濾波電容電流，則穩態時有g≈，即sum≈(1+)g≈(1+)，sum在穩態時近似與g、成正比。因此，對于電流內環，可令

并采用sum作為受控變量來設計控制器。采用前向差分法對式（17）第一式作離散化處理，有

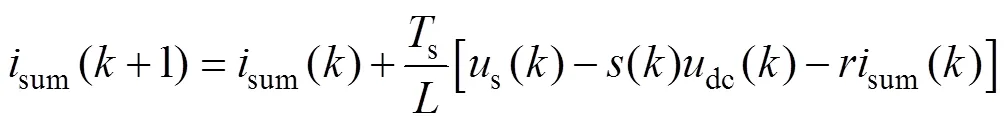
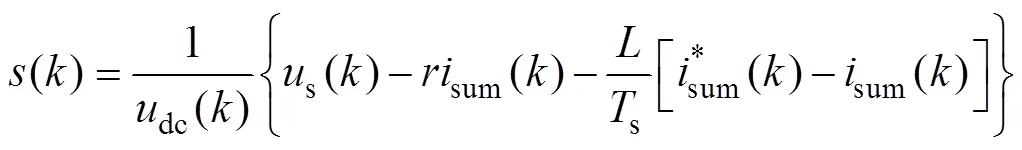
式（18）、式（20）即構成本文提出的改進無差拍控制算法。由于忽略了交流側電容電流，改進算法會導致網側偏離單位功率因數，但與文獻[27]中的簡化算法相比，改進算法引起的功率因數偏差較小。另外，改進算法的檢測變量為網側電流g和變換器側電流，將二者相減后可直接獲得濾波電容電流值，將濾波電容電流值作簡單的比例反饋即可實現有源阻尼。可見，與文獻[27]中的簡化算法相比，改進無差拍算法不僅使系統更接近單位功率因數，且利于實現有源阻尼。

在實際實現過程中，由于DSP運算處理需要時間，由第個周期采樣值計算得到的占空比直到第+1個周期才能起作用，存在一拍滯后。為了消除這種延遲的影響，可對各變量加一拍預測，即

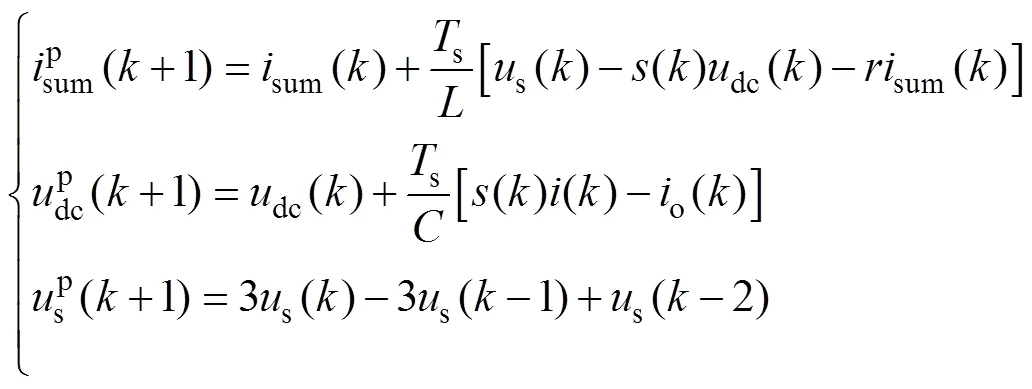
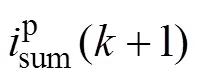
3.2 功率因數誤差分析與修正

前文已指出，當采用本文提出的改進算法或文獻[27]算法時，由于忽略了交流側電容電流，穩態時網側會偏離單位功率因數。本節將對這兩種算法造成的功率因數誤差進行分析，并針對本文算法提出一種功率因數修正方法。

（1）考慮本文提出的改進無差拍算法。此時sum被控制為與電網電壓完全同相。令s=msin(t)，sum=g+=msin(t)，m、m分別為電網電壓和sum幅值，m=(1+)，將s、sum代入式(1)第一、第二式，整理后可得

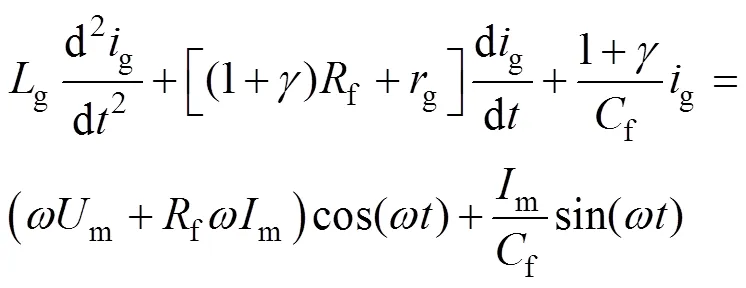
由于f、g數值較小，為了突出重點，忽略其相關項。令g=gmsin(t+g)，gm、g分別為網側電流和幅值和相位，將g代入式（22）可得

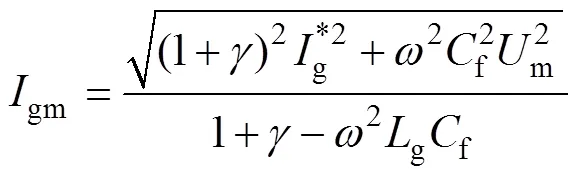
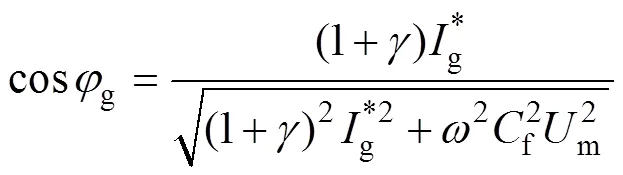
（2）考慮文獻[27]中的簡化算法。此時變換器側電流被控制為與電網電壓完全同相。令s=msin(t)，=sin(t)，g=gmsin(t+g)，類似地，可求得

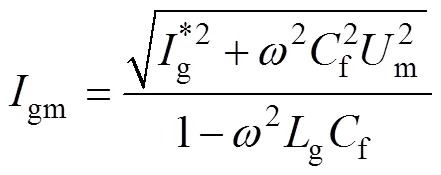
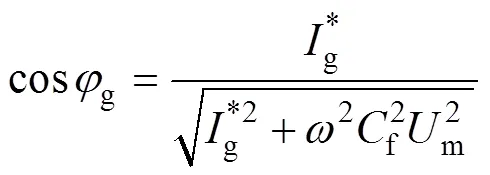
容易看出，當f=0時，對于兩種算法均有=gm，cosg=1，這是期望獲得的理想情況。由于濾波電容的存在，網側電流的幅值和相位都偏離了預期，導致電網側偏離單位功率因數。值得指出的是，比較式（24）和式（26），可以看出

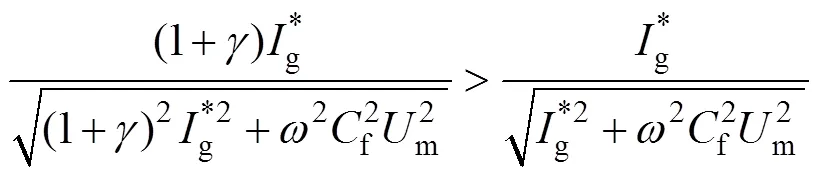
這表明，與簡化算法相比，本文提出的改進無差拍算法造成的功率因數偏差較小。

為了進一步減小功率因數偏差，針對改進算法，本節給出一種功率因數修正方法。該方法通過給sum參考值加入一定補償分量，實現精確的單位功率因數。

假定在補償分量作用下，網側電流與電網電壓實現了嚴格同相位，即滿足s=msin()，g=sin()。將此兩式代入式（1）第一、第二式，整理后可得

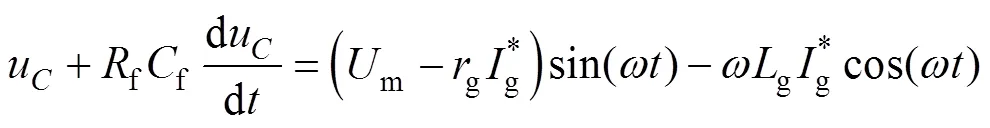
令u=cmsin(t+)，cm、分別為交流側濾波電容電壓的幅值和相位，則有

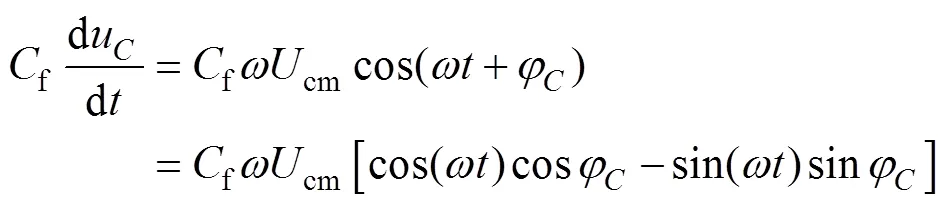
聯立式（28）、式（29），可解得

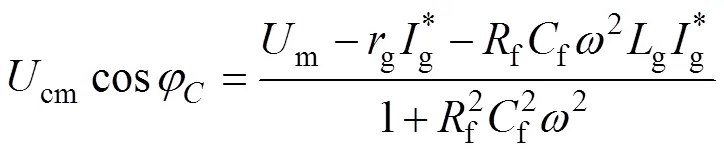
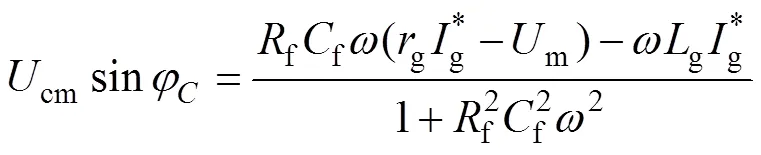
由此，可求解出

1．丹池赤水、石髓金精、山臺盡五色金。王罕嶺嵊縣峧(gǎo)的東南坡山岙，20世紀60至70年代已筑有眠牛灣水庫，庫水流出的水渠中，目前依然能看到古人所說的丹池赤水這一奇觀；在眠牛灣水庫壩大面積的護坡塊石上，同樣可以看到石髓金精、山臺盡五色金的壯麗場面。

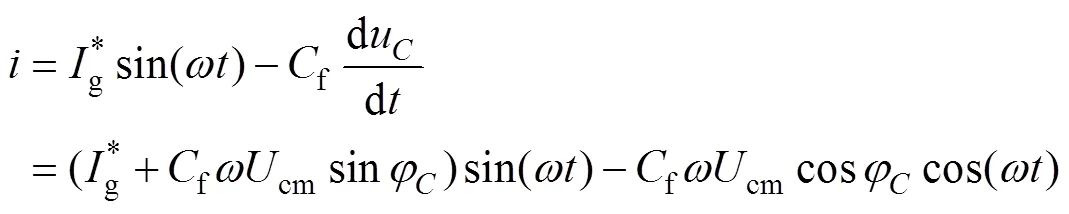
故sum的參考值應取為

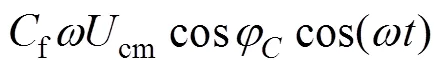
由式（33）可看出，該表達式包括一個與電網電壓同相位的分量和一個超前電網電壓90°（滯后270°）的分量。若按照式（33）設定sum參考值，則理論上能使g=sin(t)，即電網電壓與網側電流同相位，實現精確的單位功率因數。

將式（10）代入式（18）或式（33）即可形成加權和電流sum參考值。采用無差拍控制算法式（20）對該參考電流進行跟蹤，即形成了本文提出的離散趨近律與改進無差拍雙閉環控制算法。該算法不僅保留了無差拍控制高動態性能的優點，還進一步優化了電壓外環的動態響應速度，有利于系統整體性能的提升。值得注意的是，式（8）給出的參考電流有效值依賴于變換器的模型參數，且該式的推導過程忽略了附加損耗。實際電路中，由于參數失配和附加損耗的影響，若完全依賴式（8）確定參考電流，可能導致直流側電壓存在穩態誤差。為此，當直流側電壓接近參考值時，可以加入PI控制器對參考電流進行修正，以消除穩態誤差。離散趨近律與無差拍雙閉環控制算法框圖如圖2所示。

4 LCL型整流器系統欠阻尼分析及網側電流過沖消除方法

由于LCL濾波器是三階系統，在實際應用中還需考慮可能存在的諧振或欠阻尼振蕩問題，保證系統安全可靠運行。本節將結合改進無差拍控制策略對系統阻尼進行分析，指出網側電流欠阻尼振蕩可能導致暫態電流出現過沖，并提出了消除電流過沖的方法。

根據式（17），可得整流器交流側電壓rec(rec=dc)到sum的傳遞函數為

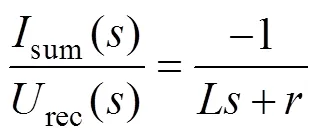
可見，若以sum為受控變量，則系統被控對象為一階慣性環節。進一步考慮sum與g的關系，將式（1）前兩式寫成與sum關聯的形式，有

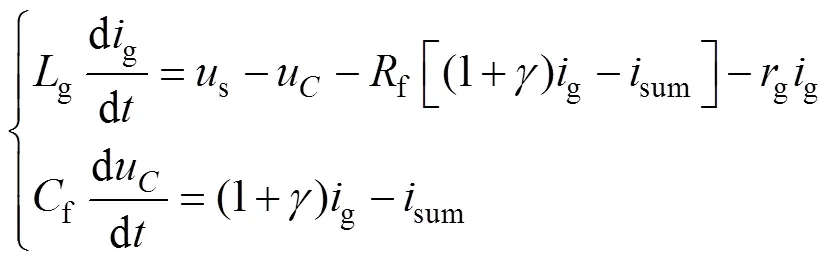
則sum到g的傳遞函數為

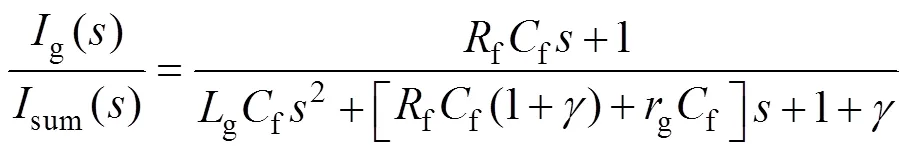
當f、g、均為零時，有

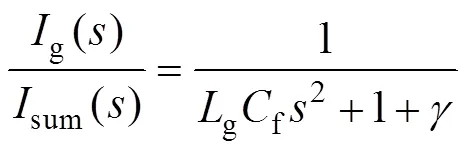
由此可見，雖然從rec到受控變量sum的傳遞函數沒有諧振點，但sum到g的傳遞函數存在諧振點。這一諧振點與rec到g傳遞函數的諧振點相同。這表明，LCL型濾波器的固有諧振點并沒有因為受控變量的改變而發生變化。進一步可看出，f能為LCL型濾波器提供額外阻尼，有效抑制諧振尖峰，這就是無源阻尼的原理。由文獻[28]可知，采用電容電流比例反饋時，也可為系統提供額外阻尼，即有源阻尼方法。當采用本文提出的改進無差拍控制策略時，由于已經檢測了網側電流和變換器側電流，可將二者作差直接得到電容電流，通過比例反饋方便地實現有源阻尼。

然而，加入無源或有源阻尼后，雖然能避免諧振的發生，但當網側電流突變時，暫態過程中仍可能出現欠阻尼振蕩現象，產生較大的暫態峰值。sum和g仿真結果如圖3所示。圖3a、圖3b分別給出了采用改進無差拍控制策略時加權和電流sum和網側電流g的仿真結果。單相PWM整流器參數見表1。仿真時采用150V恒壓源替代直流側電容，這樣可以單獨實施電流閉環控制。圖3中，=0.045s時，網側峰值電流參考值由5A階躍至10A（對應的sum峰值由6.7A階躍至13.3A）。由圖3a可看出，當參考值突變時，加權和電流迅速跟上，暫態過程沒有振蕩。這表明采用改進無差拍控制算法可以實現對sum的快速、精確控制。由圖3b可看出，網側電流g為精確的正弦波形，表明改進無差拍算法能實現精確的網側電流控制。當網側電流在峰值處由5A階躍至10A時，暫態過程中出現了欠阻尼振蕩現象，g存在較大的過沖。這是因為在設置的仿真參數下由sum到g的傳遞函數式（36）為欠阻尼系統。

為了避免由欠阻尼振蕩引起的暫態電流過沖，可將式（18）或式（33）給出的sum參考值做一階低通濾波處理，以緩解參考值變化速率，避免出現振蕩現象，即令

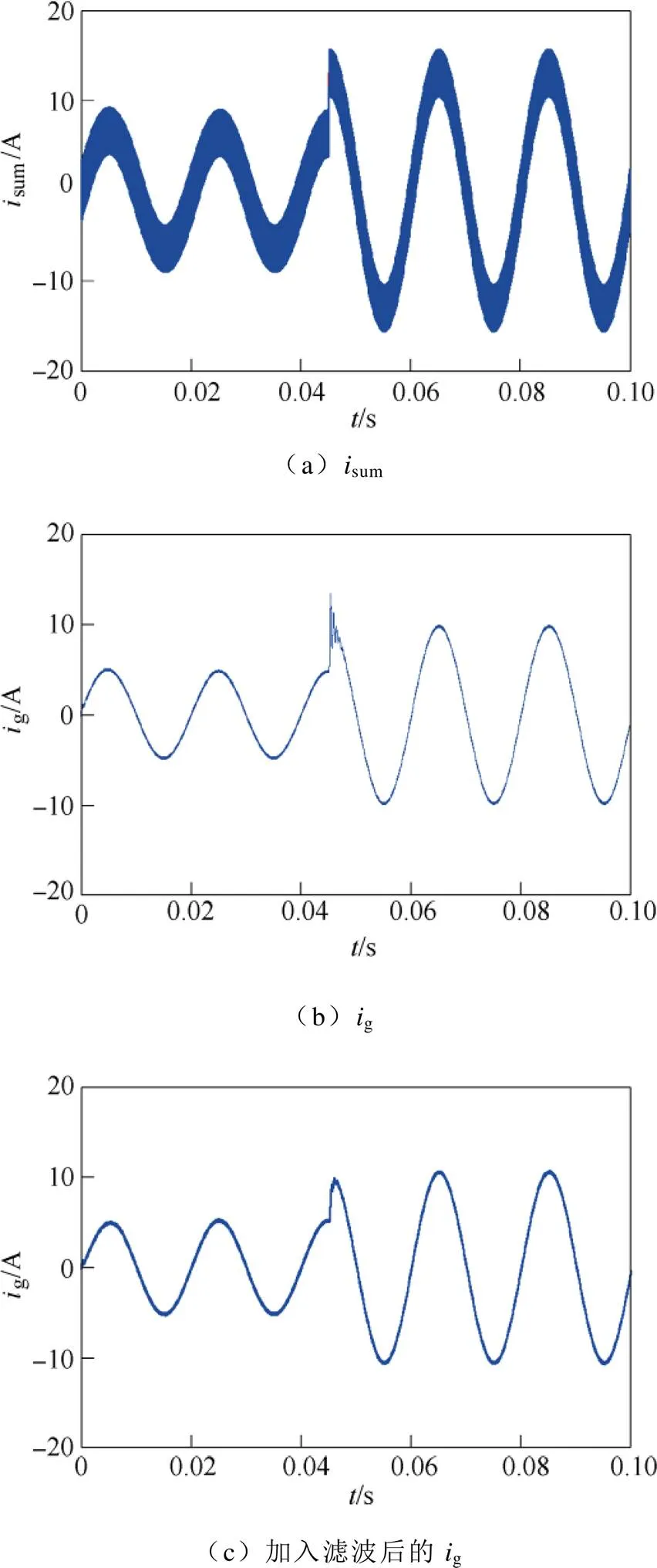
圖3 isum和ig的仿真結果

表1 單相PWM整流器參數

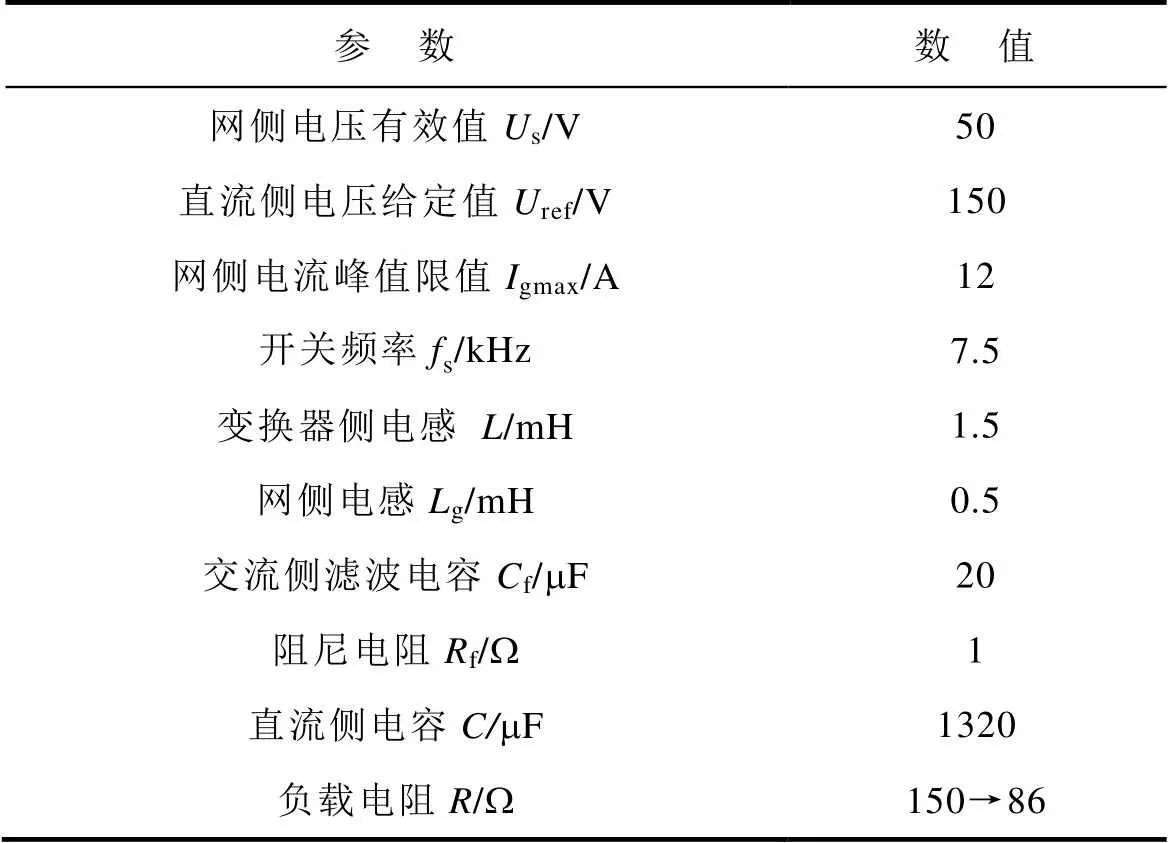
Tab.1 Parameters of the single-phase PWM rectifier

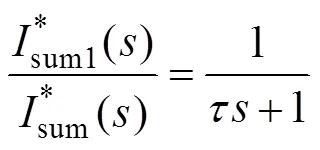
若進一步考慮濾波環節式（38）引入的相位延遲，則實現精確網側單位功率因數的sum參考值為

當 =0時，式（39）即為式（33）。

5 仿真分析

本節進一步對離散趨近律與改進無差拍雙閉環控制策略進行仿真研究，以驗證其穩態和動態性能。仿真時采用式（9）和式（20）作為控制律，采用式（39）作為sum參考值，并采用表1所示參數。

對于穩態性能，從圖4～圖7的仿真結果來看，無論穩態還是暫態，電網電壓始終和網側電流保持同相位，實現了精確的單位功率因數。圖8給出了網側電流諧波分析結果，可見網側電流總諧波畸變率（Total Harmonics Distortion, THD）為2.20%，這表明網側電流具有良好的波形質量。上述結果驗證了本文提出的改進無差拍控制算法的穩態性能。

對于動態性能，本文從輸出電壓在大偏差下的跟隨性能和負載突變時的抗擾性能兩方面進行驗證。相應地，考慮由不控整流突變為受控整流和負載突增兩種工況，分別采用PI控制和離散趨近律控制作為電壓外環控制律進行仿真（電流內環控制均采用所提出的改進無差拍算法）。

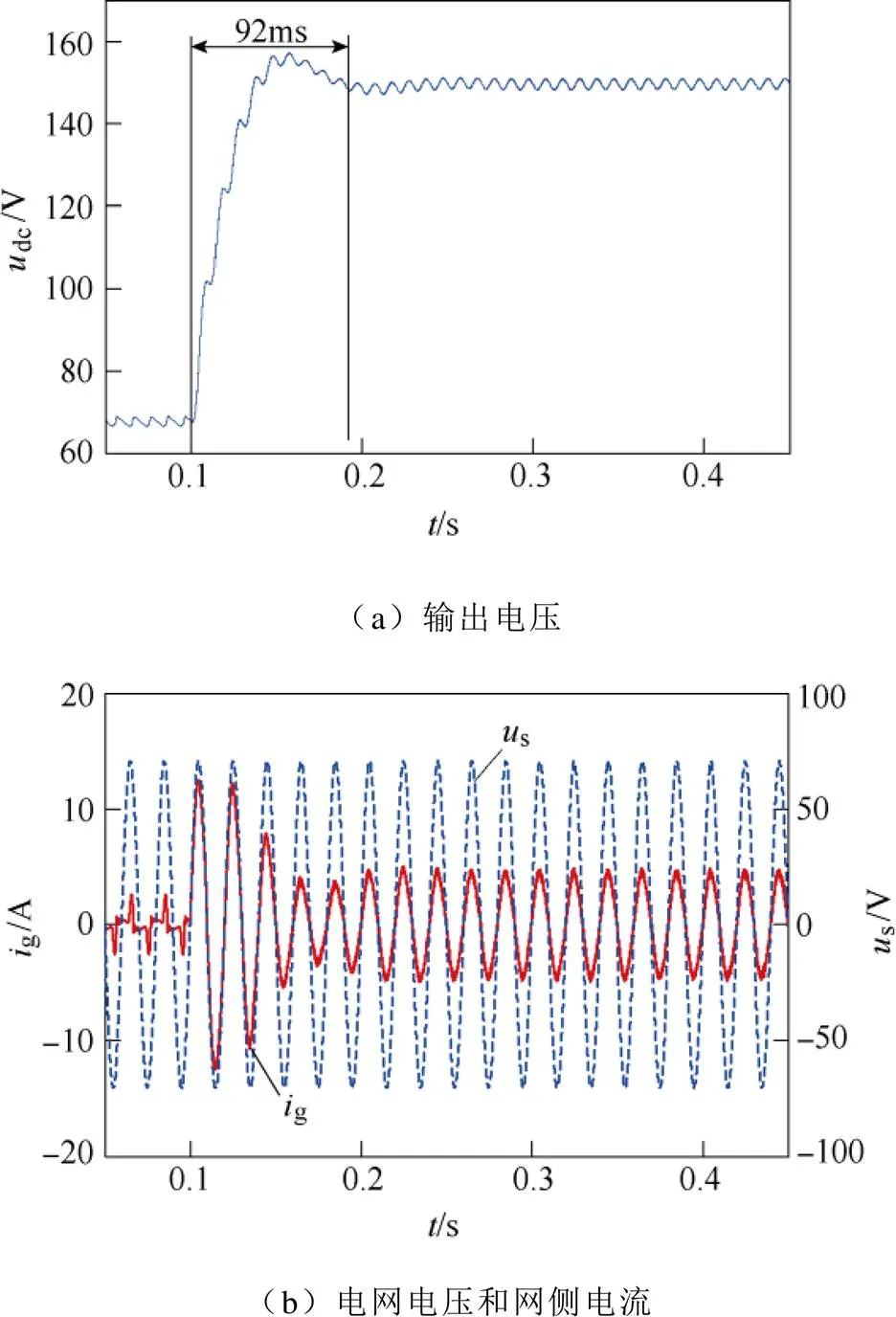
圖4 不控整流突變為受控整流仿真結果（PI控制）

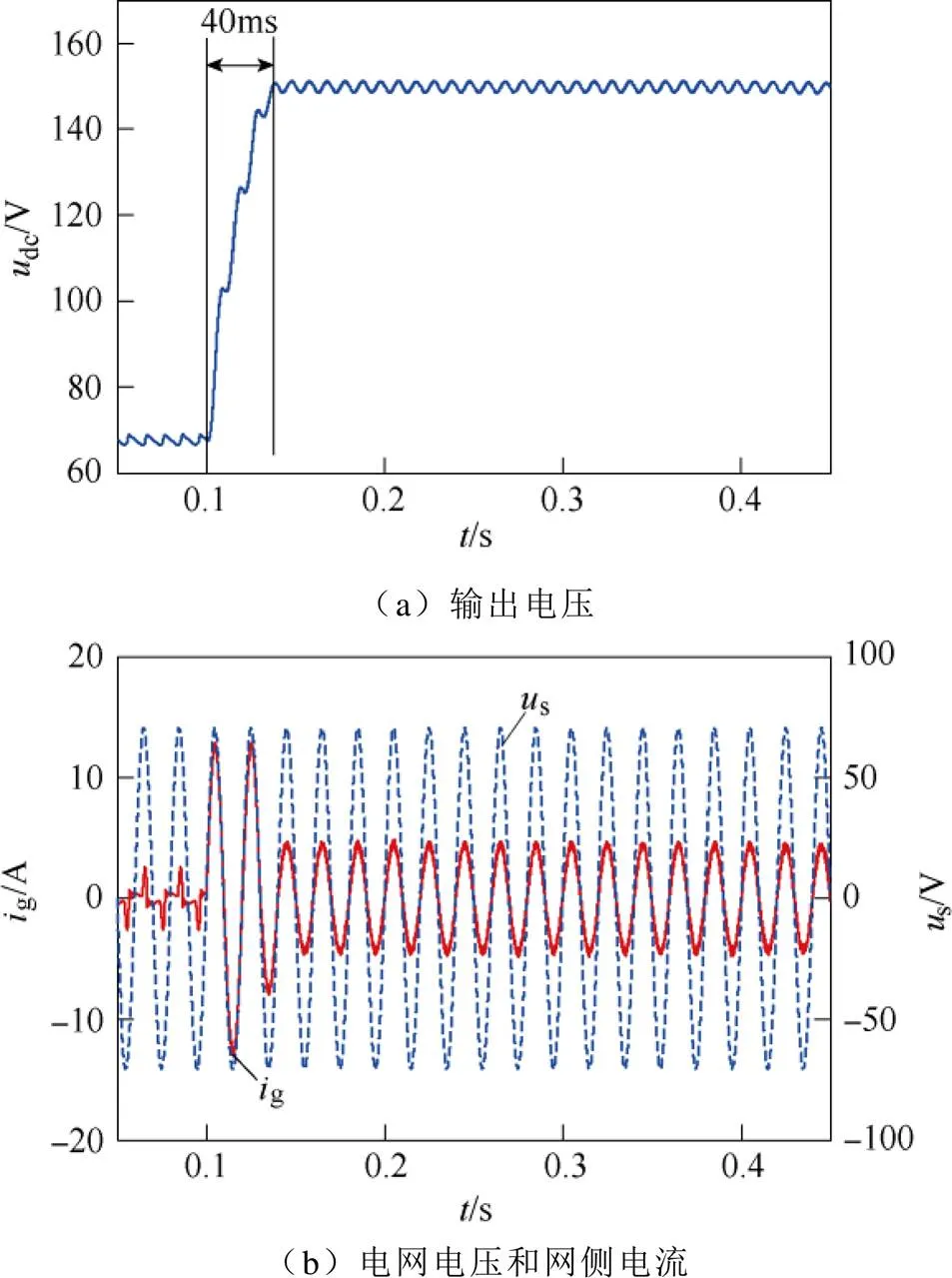
圖5 不控整流突變為受控整流仿真結果（離散趨近律控制）

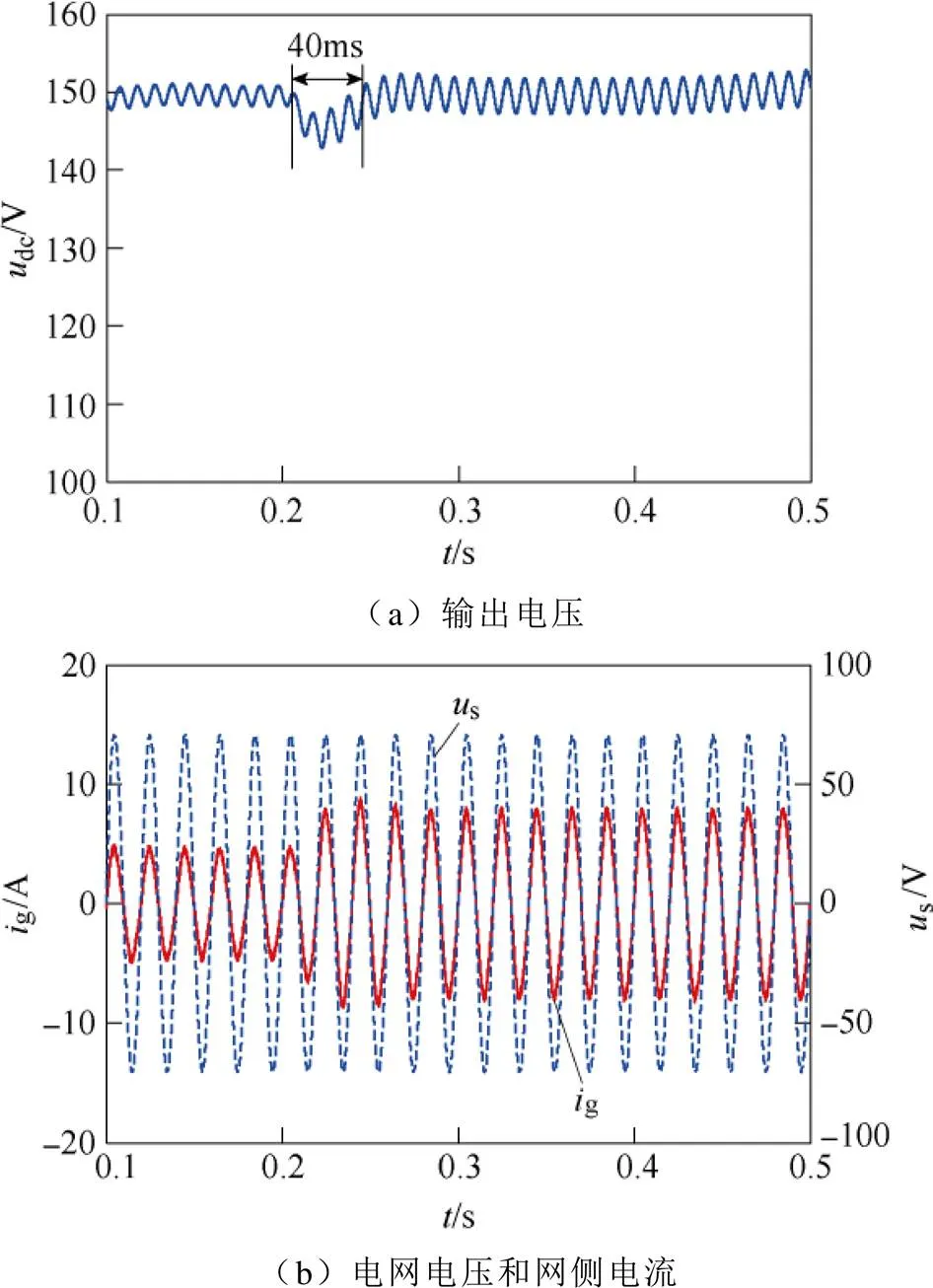
圖6 負載突增仿真結果（PI控制）

圖7 負載突增仿真結果（離散趨近律控制）

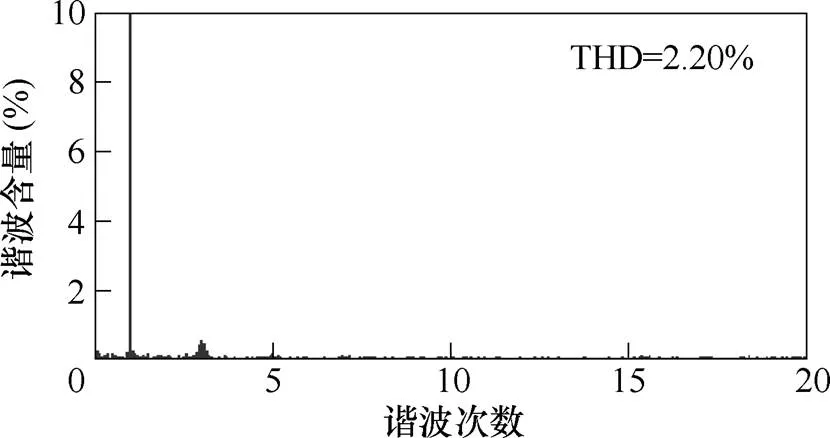
圖8 網側電流仿真數據諧波分析結果（R=86W）

圖4、圖5給出了兩種控制方式下由不控整流突變為受控整流的仿真結果，負載電阻=150W。當=0.1s時，變換器由不控整流突變為受控整流，此時輸出電壓實際值與參考值之間存在較大偏差。由圖4、圖5可看出，采用PI控制時，輸出電壓調節過程大約92ms，存在一定超調；采用離散趨近律控制時，輸出電壓經過約40ms到達穩態值，調節過程無超調。從網側電流暫態過程來看，采用離散趨近律控制時，在偏差最大的初始時刻，網側電流峰值被迅速調節至所允許的最大值，系統以允許的最大功率向直流側充電，隨著輸出電壓偏差的減小，網側電流峰值迅速被調節至穩態值。另外，無論電壓外環采用哪種控制律，網側電流g均與電網電壓s同相位，實現了精確的單位功率因數。

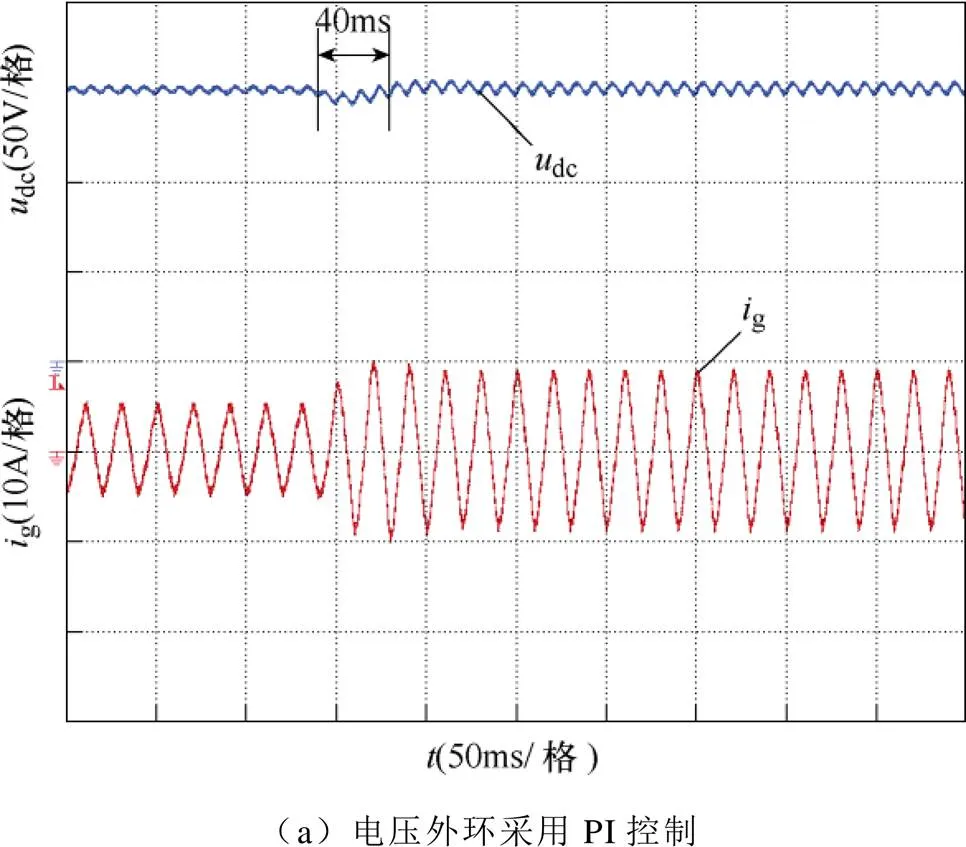
圖6、圖7給出了兩種控制方式下負載突增工況下的仿真結果。當=0.205s時，負載電阻由150W切換至86W。由圖6、圖7可看出，采用PI控制時，變換器輸出電壓出現了約40ms的短時跌落，經調節過程后重新回到穩態值；采用離散趨近律控制時，輸出電壓幾乎沒有跌落過程，始終保持為穩態值（只是在負載功率增加后二次紋波幅值增大），而網側電流峰值則被迅速調節至新的穩態值。

從仿真結果來看，電壓外環采用離散趨近律控制時，系統動態性能明顯優于采用PI控制時的情況。其原因在于，離散趨近律算法能充分利用所允許的最大網側電流向直流側充電，且能迅速調節網側電流給定值，故輸出電壓調節速度快；另一方面，離散趨近律算法能保證輸出電壓誤差按趨近律收斂，避免發生電壓超調現象，這大大縮短了系統調節時間。對比圖4b和圖5b可看出，兩種控制策略下網側電流峰值均為12A，意味著二者充電功率峰值相同。這一結果表明，即使在同等的充電功率峰值下，離散趨近律控制能提供的動態性能也明顯好于PI控制。這一優勢正是得益于離散趨近律控制能保證輸出電壓無超調。

6 實驗結果

為了進一步驗證所提算法的實用性，搭建如圖9所示的單相PWM整流器實驗平臺進行了實驗驗證。控制器采用TI公司的TMS320F28335型DSP，功率器件采用三菱公司的PS21265型IPM。實驗系統參數由表1給出，和仿真參數相同。

圖9 單相PWM整流器實驗平臺

6.1 穩態實驗

圖10給出了采用所提雙閉環控制算法時的電網電壓、網側電流穩態波形，負載電阻=86W。圖11給出了相應的網側電流諧波分析結果。由實驗結果可看出，電網電壓和網側電流完全同相位，網側電流THD＜5%，系統具有良好的穩態特性。需要指出的是，實驗中測得的網側電流THD=4.5%，高于仿真中的2.2%。這是因為實驗中測得的信號受到了電磁噪聲干擾，且實驗中使用的網側電壓含有諧波，這些非理想因素使測得的電流波形質量有所下降，但仍滿足國標要求。實驗結果再次表明，本文提出的改進無差拍控制算法能夠實現精確的網側電流控制和單位功率因數運行。

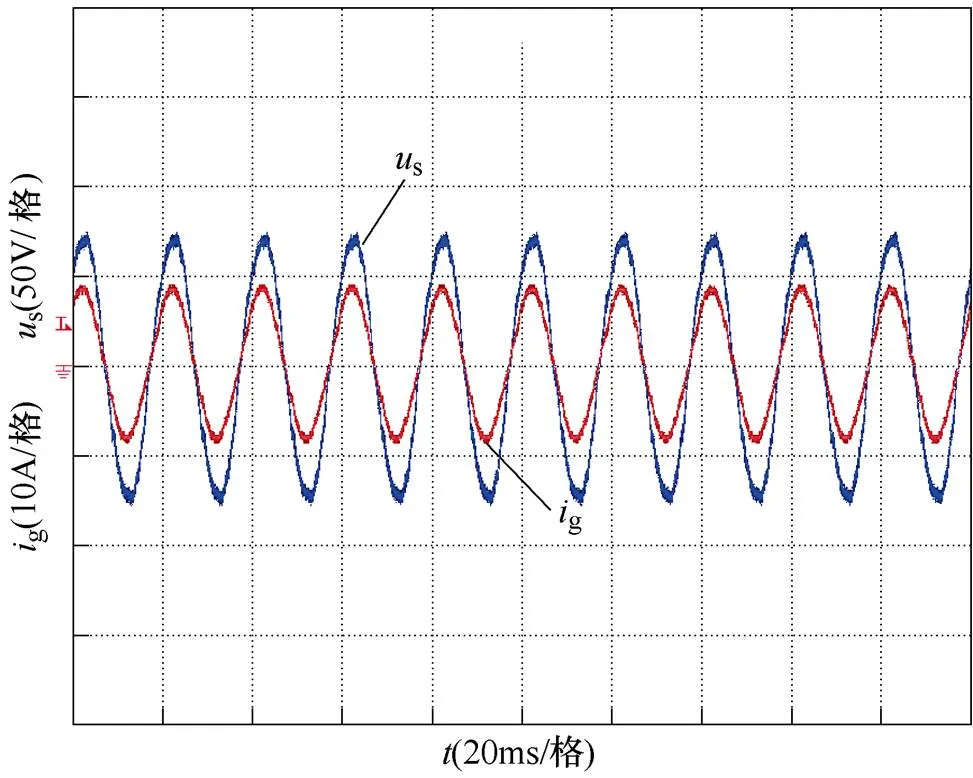
圖10 網側電流穩態實驗波形

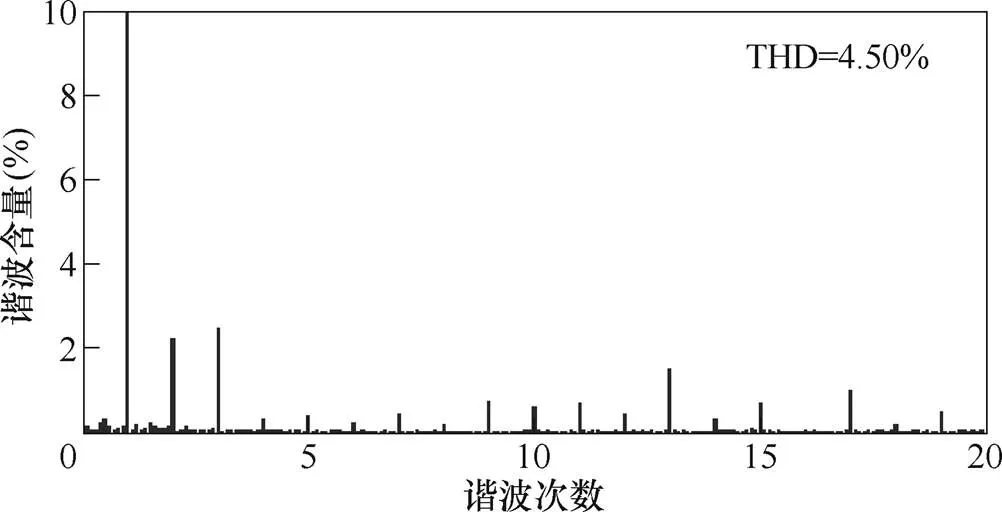
圖11 網側電流實驗數據諧波分析結果（R=86W）

6.2 動態實驗

為了驗證所提出的雙閉環算法在動態性能上的優越性，進行了不控整流到受控整流的切換實驗和負載突增實驗。實驗中分別取電壓外環控制器為PI控制和離散趨近律控制，電流內環控制器均采用改進的無差拍控制，網側電流峰值被限制在12A以下。

圖12給出了兩種電壓外環控制器下的不控整流到受控整流切換實驗結果。可以看出，當采用PI控制時，輸出電壓經過約96ms的調節時間進入穩態，且暫態過程存在超調；當采用離散趨近律控制時，輸出電壓經過約47ms到達穩態值，暫態過程無任何超調現象。這表明，相比于PI控制，離散趨近律控制在輸出電壓存在大偏差時具有更好的跟隨性能。從暫態波形和暫態過程持續時間來看，圖12的實驗結果與圖4、圖5給出的仿真結果非常相近。實驗結果中，暫態過程持續時間稍長一些，這主要是因為實驗電路與仿真模型存在一定誤差。

圖13給出了兩種電壓外環控制器下的負載突增實驗結果。實驗過程中，負載電阻由150W切換至86W，可以看出，當采用PI控制時，輸出電壓在負載突增時刻出現了大約40ms的短時跌落，網側電流經過同樣的調節時間后進入穩態；當采用離散趨近律控制時，輸出電壓在負載突增時刻幾乎沒有跌落，直接進入新的穩態，網側電流峰值迅速到達新的穩態值，基本沒有調節過程。實驗結果表明，相比于PI控制，離散趨近律控制具有更好的抗負載擾動能力。圖13的實驗結果與圖6、圖7給出的仿真結果非常相近，二者可相互印證。

7 結論

本文對單相LCL型PWM整流器的雙閉環控制策略進行了研究。為了優化電壓外環動態性能，并解決現有無差拍控制策略存在功率因數偏差的問題，本文提出了一種以離散趨近律控制為電壓外環、以改進無差拍控制為電流內環的單相LCL型PWM整流器雙閉環控制方法。通過仿真和小功率樣機實驗對以PI控制為電壓外環的雙閉環控制策略和所提出的雙閉環控制策略進行了對比研究，結果表明，本文提出的雙閉環控制策略不僅明顯改善了單相LCL型PWM整流器的動態性能，且實現了精確的網側單位功率因數。

[1] 王劍, 鄭瓊林, 高吉磊. 基于根軌跡法的單相PWM整流器比例諧振電流調節器設計[J]. 電工技術學報, 2012, 27(9): 251-256.

Wang Jian, Zheng Trllion Q, Gao Jilei. Design of current proportional-resonant regulator for single- phase PWM rectifier based on root-locus method[J]. Transactions of China Electrotechnical Society, 2012, 27(9): 251-256.

[2] Gasca M V, Garcés A, Molinas M. Stability analysis of the proportional-resonant controller in single phase converters[C]//IEEE Workshop on Power Electronics and Power Quality Applications (PEPQA), Manizales, Colombia, 2019: 1-6.

[3] 彭林, 馬磊, 劉浩然, 等. 單相PWM整流器H混合靈敏度電流控制[J]. 中國電機工程學報, 2020, 40(14): 4580-4589, 4737.

Peng Lin, Ma Lei, Liu Haoran, et al.Hmixed sensitivity current control for single-phase PWM rectifier[J]. Proceedings of the CSEE, 2020, 40(14): 4580-4589, 4737.

[4] Li Bingzhang, Huang Shenghua, Chen Xi. Perfor- mance improvement for two-stage single-phase grid- connected converters using a fast DC bus control scheme and a novel synchronous frame current controller[J]. Energies, 2017, 10(3): 389-418.

[5] 劉秉, 宋文勝. 基于虛擬信號反饋算法的單相PWM整流器DQ電流解耦控制[J]. 中國電機工程學報, 2018, 38(15): 4504-4513, 4651.

Liu Bing, Song Wensheng. DQ current decoupling control of single-phase PWM rectifiers based on virtual signal feedback algorithm[J]. Proceedings of the CSEE, 2018, 38(15): 4504-4513, 4651.

[6] 張呈象, 葛興來, 馬俊鵬, 等. 基于任意相位延時的單相整流器dq軸電流快速計算方法[J]. 中國電機工程學報, 2017, 37(21): 6400-6409.

Zhang Chengxiang, Ge Xinglai, Ma Junpeng, et al. A fast dq axis current calculation algorithm for single- phase rectifiers based on any phase-delay method[J]. Proceedings of the CSEE, 2017, 37(21): 6400-6409.

[7] 楊立永, 楊爍, 張衛平, 等. 單相PWM整流器改進無差拍電流預測控制方法[J]. 中國電機工程學報, 2015, 35(22): 5842-5850.

Yang Liyong, Yang Shuo, Zhang Weiping, et al. The improved deadbeat predictive current control method for single-phase PWM rectifiers[J]. Proceedings of the CSEE, 2015, 35(22): 5842-5850.

[8] 宋智威, 熊成林, 黃路, 等. 基于牛頓插值的單相整流器功率前饋無差拍控制[J]. 電網技術, 2018, 42(11): 3623-3629.

Song Zhiwei, Xiong Chenglin, Huang Lu, et al. Power feedback-forward and deadbeat control of single- phase rectifier based on Newton interpolation[J]. Power System Technology, 2018, 42(11): 3623- 3629.

[9] 鄧知先, 宋文勝, 曹夢華. 單相PWM整流器模型預測電流控制算法[J]. 中國電機工程學報, 2016, 36(11): 2996-3004.

Deng Zhixian, Song Wensheng, Cao Menghua. A model predictive current control scheme for single- phase PWM rectifiers[J]. Proceedings of the CSEE, 2016, 36(11): 2996-3004.

[10] 宋智威, 黃路, 熊成林, 等. 改進的單相脈沖整流器模型預測電流控制策略[J]. 電網技術, 2020, 44(5): 1845-1851.

Song Zhiwei, Huang Lu, Xiong Chenglin, et al. Improved model predictive current control strategy for single-phase pulse rectifier[J]. Power System Technology, 2020, 44(5): 1845-1851.

[11] 劉碧, 宋文勝, 孫可心, 等. 基于調制電壓橢圓軌跡優化的單相脈沖整流器模型預測電流控制[J]. 中國電機工程學報, 2018, 38(17): 5177-5188, 5315.

Liu Bi, Song Wensheng, Sun Kexin, et al. Model predictive current control of single-phase PWM rectifiers with elliptic trajectory optimization of the modulated voltage vector[J]. Proceedings of the CSEE, 2018, 38(17): 5177-5188, 5315.

[12] Tang Xiongmin, Chen Weizheng, Zhang Miao. A current decoupling control scheme for LCL-type single-phase grid-connected converter[J]. IEEE Access, 2020, 8: 37756-37765.

[13] 周樂明, 羅安, 陳燕東, 等. 單相LCL型并網逆變器功率控制及有源阻尼優化方法[J]. 電工技術學報, 2016, 31(6): 144-154.

Zhou Leming, Luo An, Chen Yandong, et al. A single-phase grid-connected power control and active damping optimization strategy with LCL filter[J]. Transactions of China Electrotechnical Society, 2016, 31(6): 144-154.

[14] 萬曉鳳, 聶曉藝, 廖志鵬, 等. 基于誤差信號反饋的單相LCL型逆變器諧振抑制方法[J]. 電機與控制學報, 2018, 22(5): 102-109.

Wan Xiaofeng, Nie Xiaoyi, Liao Zhipeng, et al. Resonance damping method of single-phase inverter with LCL-filter based on error signal feedback[J]. Electric Machines and Control, 2018, 22(5): 102- 109.

[15] 張曉, 譚力, 鮮嘉恒, 等. LCL并網逆變器預測電流控制算法[J]. 電工技術學報, 2019, 34(增刊1): 189- 201.

Zhang Xiao, Tan Li, Xian Jiaheng, et al. Predictive current control algorithm for grid-connected inverter with LCL filter[J]. Transactions of China Electro- technical Society, 2019, 34(S1): 189-201.

[16] 程國棟, 吳瑋, 夏晶晶, 等. 三相LCL并網逆變器改進模型預測控制策略[J]. 電力電子技術, 2019, 53(7): 14-17.

Cheng Guodong, Wu Wei, Xia Jingjing, et al. Improved model predictive control strategy based on three-phase LCL grid-connected inverter[J]. Power Electronics, 2019, 53(7): 14-17.

[17] 張琦, 李銳, 張永平, 等. 具有主動阻尼特征的LCL并網逆變器狀態反饋控制方法[J]. 電工技術學報, 2019, 34(8): 1698-1707.

Zhang Qi, Li Rui, Zhang Yongping, et al. Active damping method based on state-feedback for grid- connected inverter with LCL filter[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1698- 1707.

[18] Rajanna G S, Nagaraj H N. Comparison between sigmoid variable reaching law and exponential reaching law for sliding mode controlled DC-DC Buck converter[C]//International Conference on Power, Energy and Control (ICPEC), Sri Rangalatchum Dindigul, 2013: 316-319.

[19] 劉斌, 粟梅, 賀建軍, 等. 混合動力汽車DC/DC輔助電源軌跡規劃及雙積分滑模控制[J]. 電網技術, 2014, 38(4): 918-924.

Liu Bin, Su Mei, He Jianjun, et al. Trajectory planning and dual-integral sliding-mode control strategy of DC/DC auxiliary power supply for hybrid electric vehicles[J]. Power System Technology, 2014, 38(4): 918-924.

[20] 劉彥呈, 古龍瑞, 張勤進. DC-DC變換器新型趨近律滑模控制[J]. 電力系統及其自動化學報, 2018, 30(1): 64-68.

Liu Yancheng, Gu Longrui, Zhang Qinjin. Sliding mode control of DC-DC converter based on novel reaching law[J]. Proceedings of the CSU-EPSA, 2018, 30(1): 64-68.

[21] Meng Zhiqiang, Shao Wu, Tang Jie, et al. Sliding- mode control based on index control law for MPPT in photovoltaic systems[J]. CES Transactions on Elec- trical Machines and Systems, 2018, 2(3): 303-311.

[22] 李鵬瀚, 王杰, 吳飛. 雙饋風電機組次同步控制相互作用的反饋線性化滑模變結構抑制[J]. 電工技術學報, 2019, 34(17): 3661-3671.

Li Penghan, Wang Jie, Wu Fei. Sub-synchronous control interaction mitigation for DFIGs by sliding mode control strategy based on feedback linea- rization[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3661-3671.

[23] 鄭長明, 張加勝, 許睿, 等. Buck變換器的魯棒離散積分滑模控制[J].電工技術學報, 2019, 34(20): 4306-4313.

Zheng Changming, Zhang Jiasheng, Xu Rui, et al. Robust discrete integral sliding mode control for Buck converters[J]. Transactions of China Electro- technical Society, 2019, 34(20): 4306-4313.

[24] 李輝, 周鑫, 陳智勇, 等. 基于重構積分滑模變結構的虛擬無窮大電容器控制策略[J]. 中國電機工程學報, 2020, 40(13): 4340-4348.

Li Hui, Zhou Xin, Chen Zhiyong, et al. The virtual infinite capacitor control strategy based on recon- structed integral sliding mode variable structure[J]. Proceedings of the CSEE, 2020, 40(13): 4340-4348.

[25] Veselic B, Perunicic-Drazenovic B, Milosavljevic ?. Improved discrete-time sliding-mode position control using Euler velocity estimation[J]. IEEE Transactions Industrial Electronics, 2010, 57(11): 3840-3847.

[26] 劉博, 賁洪奇, 白銀龍. 一種抑制PWM整流器起動沖擊電流的緩給定方法[J]. 電工技術學報, 2018, 33(12): 2758-2766.

Liu Bo, Ben Hongqi, Bai Yinlong. A slow given method to suppress the start-up inrush current of PWM rectifier[J]. Transactions of China Electro- technical Society, 2018, 33(12): 2758-2766.

[27] He Jinwei, Li Yunwei, Bosnjak D, et al. Investigation and active damping of multiple resonances in a parallel-inverter-based microgrid[J]. IEEE Transa- ctions on Power Electronics, 2013, 28(1): 234-246.

[28] 阮新波, 王學華, 潘冬華, 等. LCL型并網逆變器的控制技術[M]. 北京: 科學出版社, 2015.

A Double Closed-Loop Control Method for Single-Phase PWM Rectifiers with LCL Filter Based on Discrete Reaching Law and Deadbeat Algorithm

（School of Electrical and Information Engineering Tianjin University Tianjin 300072 China）

For the single-phase PWM rectifier with LCL filter, the traditional double closed-loop control method usually uses PI compensator as the voltage outer loop controller, and deadbeat control, with the converter side current as the controlled variable, as the current inner loop controller. There are two problems in this scheme: one is that the integrator in the voltage outer loop will limit the dynamic performance of the system; the other is that the unit power factor on the grid side cannot be realized accurately. Thus, this paper presents a double closed-loop control method for the single-phase PWM rectifier, which takes the discrete reaching law control as the voltage outer loop controller and the improved deadbeat control as the current inner loop controller. For the voltage outer loop, the mathematical relationship between the peak value of half wave current on the grid side and the voltage increment on the DC side is derived, and a control strategy based on discrete reaching law is proposed. For the current inner loop, this paper presents an improved deadbeat algorithm with the weighted sum of the grid side current and converter side current as the controlled variable, and derives the current reference for achieving the accurate unit power factor. This paper also discusses the current overshoot caused by the under-damped oscillation, and puts forward the solution. Simulation and experimental results show that the proposed control strategy improves the dynamic performance of the system and achieves accurate unit power factor on the grid side.

Single-phase PWM rectifier, LCL filter, discrete reaching law, deadbeat control, under-damped oscillation

TM46

10.19595/j.cnki.1000-6753.tces.200100

2020-02-04

2020-05-25

李景灝 男，1990年生，博士研究生，研究方向為電力電子與電力傳動。E-mail: lijinghao@tju.edu.cn（通信作者）

吳愛國 男，1954年生，教授，博士生導師，研究方向為電力電子變換器與非線性控制技術。E-mail: agwu@tju.edu.cn

（編輯 陳 誠）