深度學(xué)習(xí) 自主關(guān)聯(lián) 發(fā)現(xiàn)規(guī)律
——《分?jǐn)?shù)的基本性質(zhì)》教學(xué)設(shè)計(jì)

文｜郭 文

【教學(xué)內(nèi)容】

人教版五年級(jí)下冊(cè)第57 頁例1 及相關(guān)練習(xí)。

【教學(xué)過程】

一、問題驅(qū)動(dòng)，導(dǎo)入新課

教師開門見山，直接引入課題，板書課題。

師：讀了課題后你有什么問題？

（板書學(xué)生提出的問題：1.什么是分?jǐn)?shù)的基本性質(zhì)？2.為什么叫分?jǐn)?shù)的基本性質(zhì)？3.學(xué)習(xí)分?jǐn)?shù)的基本性質(zhì)有什么作用？4.分?jǐn)?shù)的基本性質(zhì)怎么來的？）

師：愛因斯坦說“提出一個(gè)問題往往比解決一個(gè)問題更重要。”你們真會(huì)提問！讓我們帶著這些問題，一起學(xué)習(xí)分?jǐn)?shù)的基本性質(zhì)。

【設(shè)計(jì)意圖：“學(xué)起于思，思源于疑。”直接引入新課，學(xué)生積極大膽地提出問題，帶著自己提出的問題參與學(xué)習(xí)，學(xué)習(xí)積極性高、目的性強(qiáng)。】

二、探究、理解分?jǐn)?shù)的基本性質(zhì)

（1）創(chuàng)設(shè)情境，引發(fā)思考。

師：我們的學(xué)習(xí)從一個(gè)故事開始。話說唐僧師徒四人一路跋山涉水、翻山越嶺、饑腸轆轆。悟空化來餅，把一個(gè)餅平均分成2份，給八戒1 塊，說“八戒給你這張餅的吧！”八戒一看，說“不行，太少了！”于是悟空把這張餅平均分成4 份，說“那就給你這張餅的吧！”八戒還嫌少。悟空又把這張餅平均分成8 份，說“那就給你這張餅的吧！”八戒一看，開心地說“這還差不多！”聽完故事，你想說什么？

生：八戒真傻！

（2）小組合作，操作探究。

師：有三個(gè)分?jǐn)?shù)，小組里的三位同學(xué)先商量一下怎么分工。

師：全班都商量好了，那我們就開始用長(zhǎng)方形紙畫一畫、折一折、涂一涂。給大家2 分鐘的時(shí)間。

師：時(shí)間到。現(xiàn)在三人小組看著你們的長(zhǎng)方形交流一下。

（3）全班交流，驗(yàn)證猜想。

師：請(qǐng)看，這是三個(gè)小組的作品。（找三個(gè)小組，把不同的折長(zhǎng)方形的方法和畫線段圖的方法貼在黑板上）

方法一

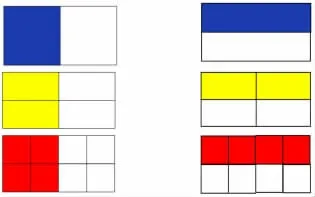
方法二

方法三

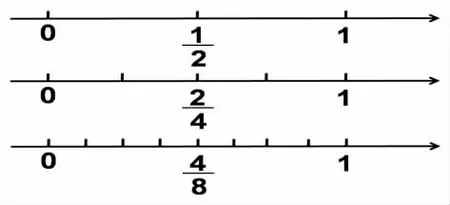
【設(shè)計(jì)意圖：創(chuàng)設(shè)生動(dòng)有趣的悟空給八戒分餅的問題情境，學(xué)生在理解分?jǐn)?shù)意義的基礎(chǔ)上，借助數(shù)形結(jié)合，將相等的分?jǐn)?shù)與直觀圖形建立關(guān)聯(lián)，于“提出猜想——操作驗(yàn)證——得到結(jié)論”的數(shù)學(xué)活動(dòng)中，清晰地觀察到都是一半，建構(gòu)了，為理解、抽象、概括分?jǐn)?shù)的基本性質(zhì)積累經(jīng)驗(yàn)。三人小組的形式進(jìn)行小組合作探究，并在探究前商量分工情況，增強(qiáng)了小組合作學(xué)習(xí)的效果，讓每位學(xué)生都真正參與合作學(xué)習(xí)。】

2.舉例驗(yàn)證，發(fā)現(xiàn)規(guī)律。

（1）引發(fā)沖突，深入思考發(fā)現(xiàn)規(guī)律。

師：我也說一個(gè)，我想給八戒3 份，那應(yīng)該平均分成幾份呢？你怎么想的？

生：給八戒3 份就要把這個(gè)餅平均分成6 份，因?yàn)? 是6 的一半。

師：給八戒7 份呢？給八戒10 份呢？給八戒37 份呢？如果平均分成26 份，給八戒幾份？平均分成50 份，給八戒幾份？10000 份呢？

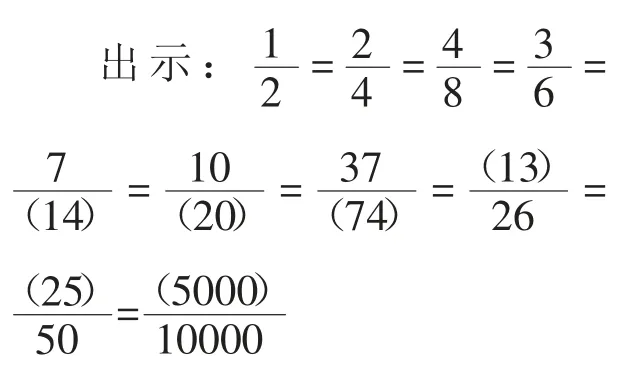
師：觀察這些分?jǐn)?shù)，你發(fā)現(xiàn)了什么？

師：了不起的發(fā)現(xiàn)！分?jǐn)?shù)的分子和分母都乘同一個(gè)整數(shù)、小數(shù)，分?jǐn)?shù)的大小不變。剛剛從左往右看，如果從右往左看呢？

生：從右往左看，分?jǐn)?shù)的分子和分母都除以幾，分?jǐn)?shù)的大小不變。

生：除以的數(shù)不能是0。因?yàn)? 不能作除數(shù)。

師：怎樣把我們的發(fā)現(xiàn)用一句話說一說？同桌交流交流。

（全班交流后指名匯報(bào)）

生：分?jǐn)?shù)的分子和分母都乘幾或除以幾（0 除外），分?jǐn)?shù)的大小不變。

生：這里的“幾”是同一個(gè)數(shù)。

生：同一個(gè)數(shù)可以是整數(shù)，也可以是小數(shù)。

生：分?jǐn)?shù)的分子和分母同時(shí)乘或除以相同的數(shù)（0 除外），分?jǐn)?shù)的大小不變。

【設(shè)計(jì)意圖：教師巧妙地借助悟空分餅的問題情境，提出問題“如果你是悟空，你還會(huì)怎么捉弄八戒？”更是激發(fā)了學(xué)生的求知欲，學(xué)生說出與相等的分?jǐn)?shù)，不僅加深了學(xué)生對(duì)這三個(gè)分?jǐn)?shù)的認(rèn)識(shí)，拓展了學(xué)生對(duì)“一半”的理解，還積累了多個(gè)與相等的分?jǐn)?shù)，為觀察、分析、發(fā)現(xiàn)分?jǐn)?shù)的基本性質(zhì)做好素材鋪墊。教師作為學(xué)生學(xué)習(xí)活動(dòng)的參與者，提出“我想給八戒3 份，那應(yīng)該平均分成幾份呢？”引發(fā)認(rèn)知沖突，把學(xué)生的思維引向深入，學(xué)生互相質(zhì)疑、辯解并最終理解。學(xué)生認(rèn)識(shí)到與相等的分?jǐn)?shù)不僅可以乘或除以偶數(shù)，還可以乘或除以奇數(shù)，逐步逼近分?jǐn)?shù)的基本性質(zhì)，探尋數(shù)學(xué)知識(shí)的本質(zhì)。在師生、生生的交往互動(dòng)中，學(xué)生對(duì)分?jǐn)?shù)的基本性質(zhì)的認(rèn)知得到擴(kuò)展，乘或除以的數(shù)可以是整數(shù)，也可以是小數(shù)，只要是相同的數(shù)就行。學(xué)生在經(jīng)歷了觀察、分析、比較等活動(dòng)后，對(duì)分?jǐn)?shù)的基本性質(zhì)的理解更深入、更豐滿、更全面，學(xué)生的抽象、推理能力得到了發(fā)展。同時(shí)，也實(shí)現(xiàn)了深度學(xué)習(xí)。】

（2）舉例驗(yàn)證，豐富認(rèn)知。

師：還有什么發(fā)現(xiàn)？

生：我發(fā)現(xiàn)，黑板上的分?jǐn)?shù)都是真分?jǐn)?shù)，假分?jǐn)?shù)是不是也這樣呢？

師：要想知道假分?jǐn)?shù)是不是這樣？怎么辦？

生：舉例子驗(yàn)證。

師：好辦法！我們舉假分?jǐn)?shù)的例子試一試。

（學(xué)生獨(dú)立在本子上舉例子）

師：誰來說說你舉的例子？

生：帶分?jǐn)?shù)可以化成整數(shù)和真分?jǐn)?shù)，所以帶分?jǐn)?shù)的分子和分母都乘或除以幾（0 除外），分?jǐn)?shù)的大小不變。

師：這樣的例子能舉多少個(gè)？（無數(shù)個(gè)）通過剛才舉例驗(yàn)證，我們發(fā)現(xiàn)不管是真分?jǐn)?shù)、假分?jǐn)?shù)，還是帶分?jǐn)?shù)的分子和分母同時(shí)乘或除以相同的數(shù)（0 除外），分?jǐn)?shù)的大小不變。這就叫分?jǐn)?shù)的基本性質(zhì)。

3.溝通聯(lián)系，加深理解。

師：看著分?jǐn)?shù)的基本性質(zhì)，你會(huì)想到什么？

生：我想到了被除數(shù)和除數(shù)同時(shí)乘或除以相同的數(shù)（0 除外），商不變。

生：分?jǐn)?shù)的分子相當(dāng)于被除數(shù)，分母相當(dāng)于除數(shù)，所以分?jǐn)?shù)的基本性質(zhì)和商不變的規(guī)律是一樣的。

師：分?jǐn)?shù)與除法有著密切的關(guān)系，看著分?jǐn)?shù)的基本性質(zhì)他想到了商不變的規(guī)律。融會(huì)貫通，非常會(huì)學(xué)習(xí)！

【設(shè)計(jì)意圖：分?jǐn)?shù)的基本性質(zhì)在教材中僅出現(xiàn)了真分?jǐn)?shù)，整節(jié)課的學(xué)習(xí)均采用“自主學(xué)習(xí)的教學(xué)范式”，學(xué)生能夠自主關(guān)聯(lián)，由真分?jǐn)?shù)想到假分?jǐn)?shù)、帶分?jǐn)?shù)，全班舉例驗(yàn)證，得出之所以叫分?jǐn)?shù)的基本性質(zhì)，是因?yàn)樗械姆謹(jǐn)?shù)都具有此性質(zhì)，進(jìn)而豐富學(xué)生的認(rèn)知；由分?jǐn)?shù)的基本性質(zhì)想到商不變的規(guī)律，主動(dòng)把新舊知識(shí)進(jìn)行關(guān)聯(lián)，在分?jǐn)?shù)的基本性質(zhì)的基礎(chǔ)上去思考解釋商不變的規(guī)律，強(qiáng)化知識(shí)間的關(guān)聯(lián)與遞進(jìn)，從“知識(shí)點(diǎn)”走向“知識(shí)結(jié)構(gòu)”。】

4.回顧問題，有始有終。

師：回顧上課伊始我們提出的問題，每一個(gè)問題都有答案了嗎？什么是分?jǐn)?shù)的基本性質(zhì)？

生：分?jǐn)?shù)的分子和分母同時(shí)乘或除以相同的數(shù)（0 除外），分?jǐn)?shù)的大小不變。

師：為什么叫分?jǐn)?shù)的基本性質(zhì)？

生：因?yàn)檫@是真分?jǐn)?shù)、假分?jǐn)?shù)、帶分?jǐn)?shù)都有的性質(zhì)，所以叫分?jǐn)?shù)的基本性質(zhì)。

師：分?jǐn)?shù)的基本性質(zhì)是怎么來的？

生：剛剛我們通過折一折、涂一涂、畫一畫、舉例子等方法得到的。

師：最后一個(gè)問題，學(xué)習(xí)分?jǐn)?shù)的基本性質(zhì)有什么作用？我們下面試一試。

【設(shè)計(jì)意圖：回顧學(xué)生提出的問題，既對(duì)本節(jié)課的學(xué)習(xí)進(jìn)行了總結(jié)，又培養(yǎng)了學(xué)生有始有終的好習(xí)慣。】

三、應(yīng)用知識(shí)，體會(huì)價(jià)值

1.填一填。

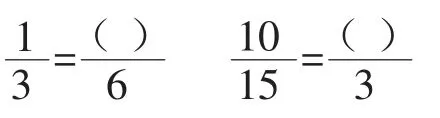
（學(xué)生獨(dú)立完成，全班訂正時(shí)讓學(xué)生說一說為什么這樣填）

2.小游戲——變魔術(shù)。

四、全課小結(jié)

師：這節(jié)課，我們一起學(xué)習(xí)了分?jǐn)?shù)的基本性質(zhì)，你有什么收獲呢？

【設(shè)計(jì)意圖：練習(xí)題的設(shè)計(jì)少而精，把例2 的教學(xué)融入其中，當(dāng)學(xué)生理解了分?jǐn)?shù)的基本性質(zhì)之后，顯得輕而易舉、水到渠成。】

深度學(xué)習(xí)是實(shí)現(xiàn)核心素養(yǎng)的重要途徑。《分?jǐn)?shù)的基本性質(zhì)》一課教學(xué)中，教師讓學(xué)生自己提出本節(jié)課探究的問題，把學(xué)習(xí)的主動(dòng)權(quán)交還給學(xué)生；創(chuàng)設(shè)悟空分餅的問題情境，學(xué)生親歷分?jǐn)?shù)的基本性質(zhì)的發(fā)現(xiàn)、驗(yàn)證、完善過程，在一系列問題解決的過程中“悟道理”，實(shí)現(xiàn)對(duì)分?jǐn)?shù)的基本性質(zhì)的理解、應(yīng)用與創(chuàng)造；由學(xué)會(huì)知識(shí)走向?qū)W會(huì)思維，對(duì)分?jǐn)?shù)基本性質(zhì)的認(rèn)識(shí)既“深”下去，又“遠(yuǎn)”開來，學(xué)生既長(zhǎng)知識(shí)又長(zhǎng)智慧、長(zhǎng)見識(shí)、長(zhǎng)能力。