階梯形轉子對雙定子磁通反向電機齒槽轉矩的影響

鄒定琛，曹江華

(華南理工大學 電力學院，廣州 510641)

0 引 言

雙定子磁通反向電機是一種新型雙凸極電機，由傳統的磁通反向電機演變而來，具有結構簡單、容錯性強、轉動慣量小等特點，在電動汽車、航空航天、風力發電等場合具有廣闊應用前景[1-2]。傳統的磁通反向電機的永磁體和繞組放在同一側定子上，而雙定子磁通反向電機的永磁體和繞組分別放置在內、外定子上。在結構上，雙定子結構有助于增大定子繞組的放置空間，減小永磁體的用量，提高對電機內腔的利用率；在電磁性能上，雙定子結構能夠進一步減少漏磁，提升轉矩密度；在散熱上，由于永磁體和繞組分離放置在靜止的兩側定子上，更方便散熱管理[3]，從而降低永磁體退磁風險[4]。但是，由于其結構特殊，雙定子磁通反向電機的齒槽轉矩也比較大[5-6]，作為電動機使用時，會影響輸出轉矩的平穩度，作為發電機使用時，會導致起動困難，同時齒槽轉矩還會引起噪聲和振動，尤其是在低速情況下，這種影響更為嚴重。因此，必須對該類電機的齒槽轉矩加以重視，到目前為止，已經有學者對其進行了研究，并取得了一定的成果[7]。

目前，削弱齒槽轉矩的主要方法有：分數槽繞組、極弧系數匹配、斜極或斜槽、永磁體分段、開輔助槽等[8-10]。文獻[7]基于磁共能-磁勢模型，推導了傳統的磁通反向電機齒槽轉矩解析模型，采用改變定轉子齒寬配合的方法來降低齒槽轉矩；文獻[10-11]研究了永磁體削角、轉子開輔助槽和斜槽對磁通反向電機的影響；文獻[12-13]提出轉子大小齒間隔加分段結構來減小齒槽轉矩；文獻[14]研究了不同的定轉子極數配合對雙定子磁通反向電機齒槽轉矩的影響；文獻[15-17]提出了采用偏心角削齒結構來削弱齒槽轉矩；文獻[18]提出采用階梯齒轉子來削弱磁通切換電機的齒槽轉矩，在大幅度削弱齒槽轉矩的同時能保持其電磁性能，但并未深入研究階梯齒參數對電機齒槽轉矩和電磁性能的影響。我國對磁通反向電機齒槽轉矩的研究起步較晚[7]，對于雙定子磁通反向電機的研究更是鳳毛麟角，深入分析雙定子磁通反向電機齒槽轉矩關鍵參數迫在眉睫。

本文基于磁共能法，以12/10極雙定子磁通反向電機為例，推導了雙定子磁通反向電機在傳統轉子下的齒槽轉矩解析模型，提出采用階梯形轉子來抑制齒槽轉矩，闡釋了階梯形轉子抑制齒槽轉矩的原因。在此基礎上，利用有限元方法，研究了階梯形轉子各層階梯的極弧系數對齒槽轉矩和電磁性能的影響。最后，將全局優化算法與有限元法相結合，對階梯形轉子參數進行優化，結果表明，該方法可以有效地削弱齒槽轉矩并改善電磁性能。

1 階梯形轉子削弱齒槽轉矩的原理

1.1 12/10極雙定子磁通反向電機工作原理

圖1給出了12/10極傳統雙定子磁通反向電機的結構，其工作原理與傳統磁場調制電機相同。

圖1 傳統雙定子磁通反向電機截面圖

表貼在內定子上的永磁體經過轉子塊的調制作用，形成旋轉的磁場；外定子通入三相對稱電流，形成旋轉的磁動勢，二者相互作用，產生恒定的電磁轉矩。對于不同類型的磁場調制電機，都具有相同的運行規則[3]：

θe=Q·θm

(1)

(2)

式中：θe和θm分別為轉子位置的電角度和機械角度；Q為轉子塊數；n為轉速；f為頻率。

1.2 雙定子磁通反向電機齒槽轉矩

由于雙定子磁通反向電機具有兩層氣隙結構，而氣隙中的電磁能量大部分集中在靠近永磁體側的內氣隙，為了簡化分析，暫且忽略外層氣隙對齒槽轉矩的影響，只對其內氣隙建立齒槽轉矩解析模型并進行定性分析。

根據能量法，齒槽轉矩可以表示為定子繞組不通電時，電機內部的磁共能W和相對位置角α的負導數，即：

(3)

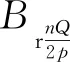
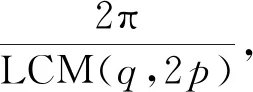
對于傳統轉子，其氣隙磁導可以用傅里葉展開：

(4)

由圖3(a)可以得出，傳統轉子的有效氣隙長度在一個轉子塊的周期內的分布函數:

(5)

由此可得:

(6)

對式(6)進行傅里葉展開，可得傳統轉子氣隙磁導諧波幅值:

(7)

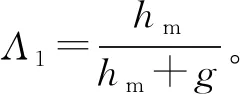
根據式(3)和式(7)，若在不改變永磁體參數的情況下減小齒槽轉矩，必須想辦法減小Λgn。

為了減小Λgn，可以使用階梯形轉子來代替傳統轉子，如圖2所示。

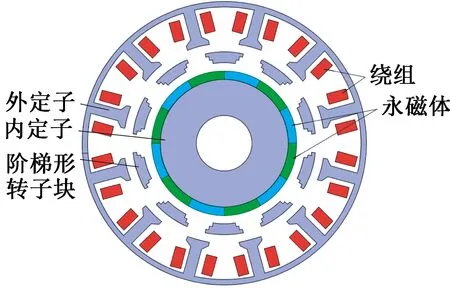
圖2 階梯形轉子雙定子磁通反向電機截面圖

對于階梯形轉子，由圖3(b)可以得出，其有效氣隙長度在一個轉子塊周期內的分布函數：

(8)

由此可得，階梯形轉子的氣隙磁導：

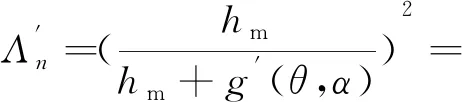
(9)

對式(9)進行傅里葉展開，可得階梯形轉子氣隙磁導諧波幅值:

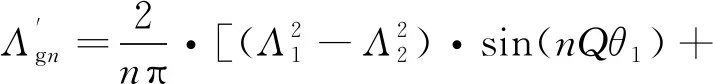
(10)

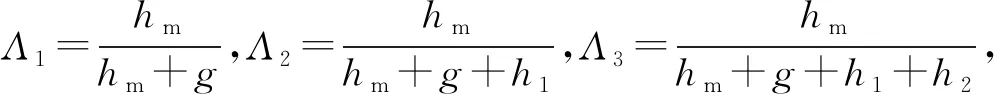
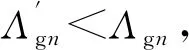
1.3 傳統轉子和階梯形轉子齒槽轉矩有限元驗證

如圖3所示，定義轉子塊的極弧系數：

(11)

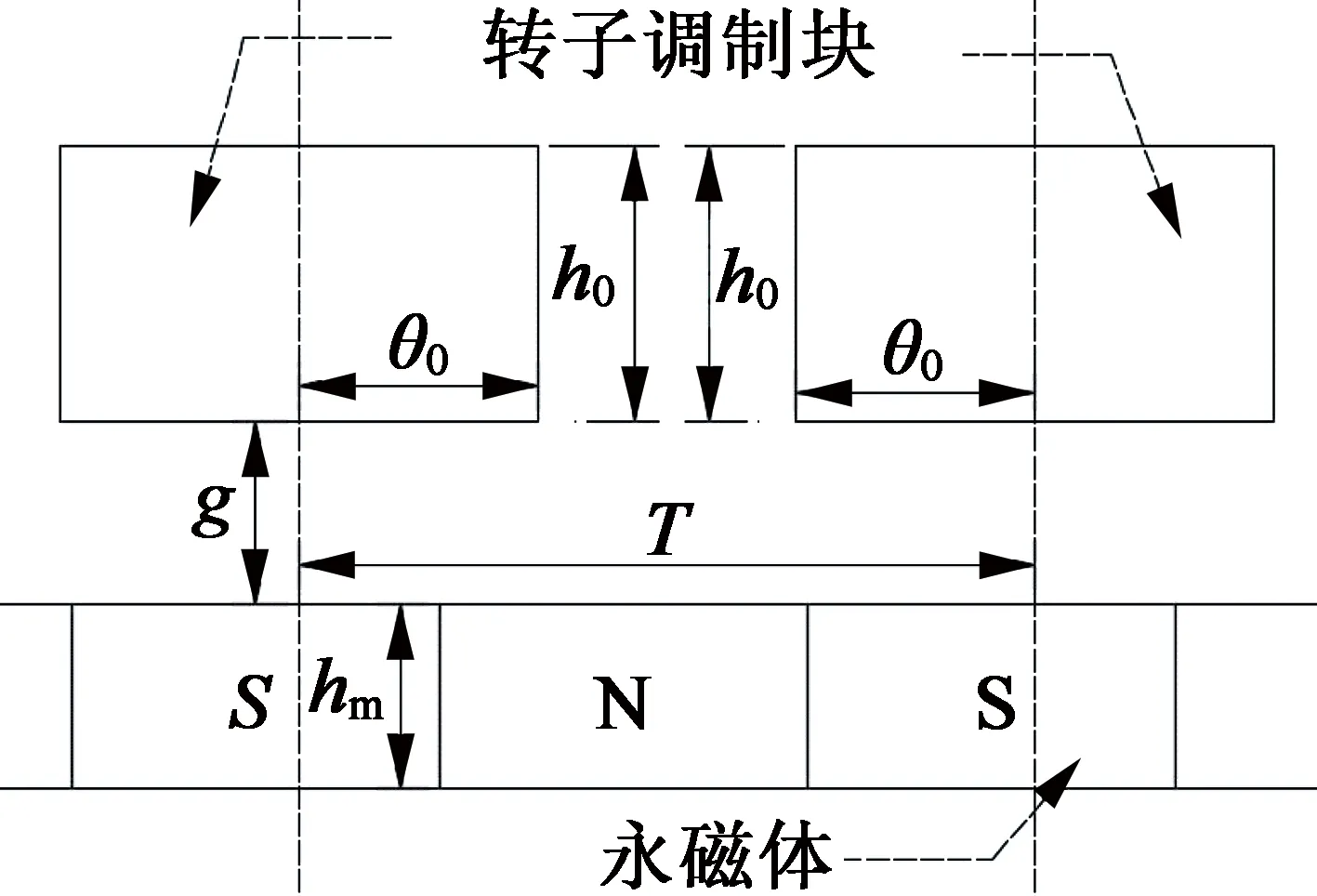
(a) 永磁體和傳統轉子相對位置

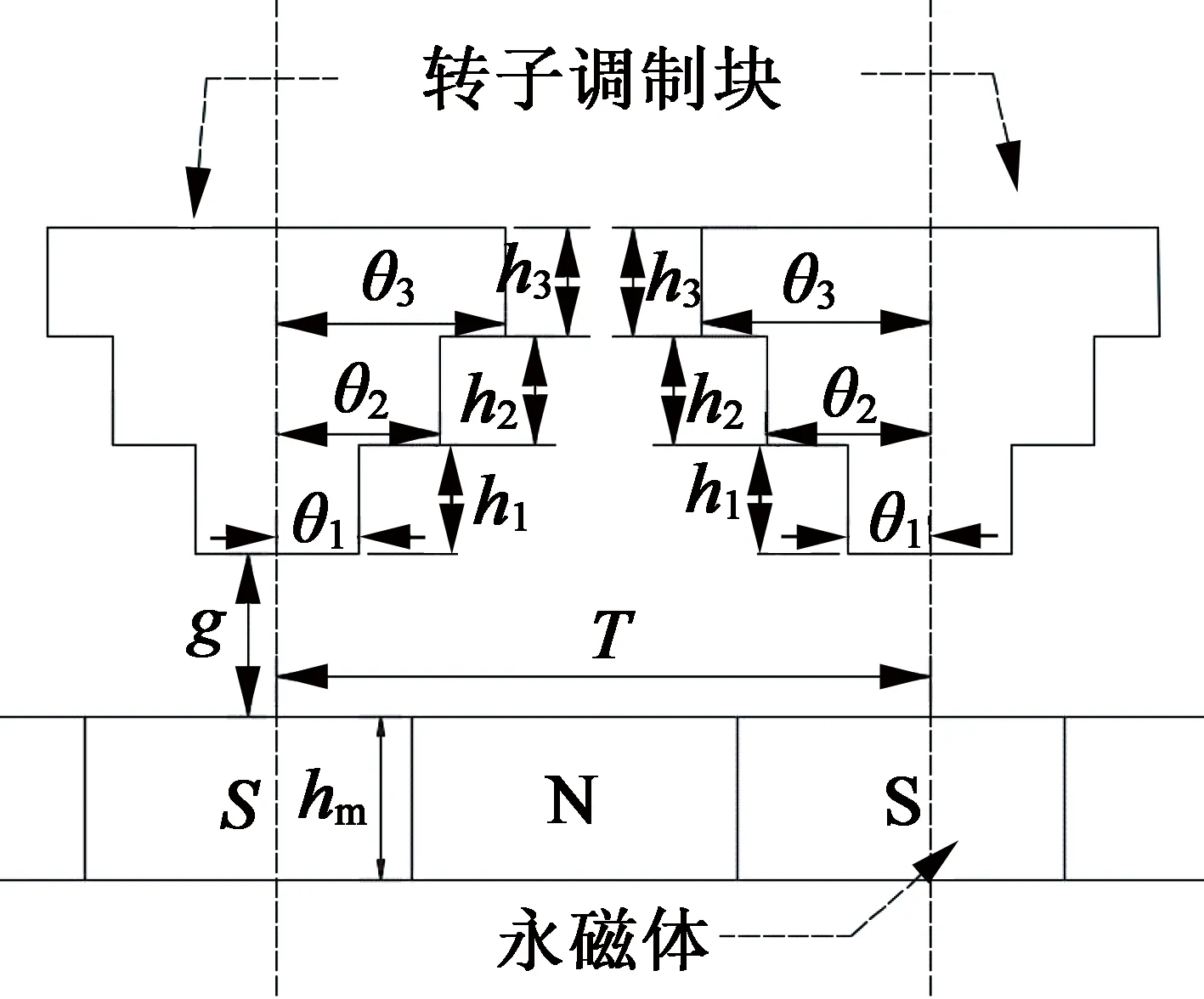
(b) 永磁體和階梯形轉子相對位置

式中：T=2π/Q為轉子塊的周期。

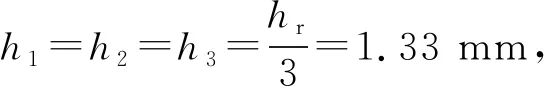
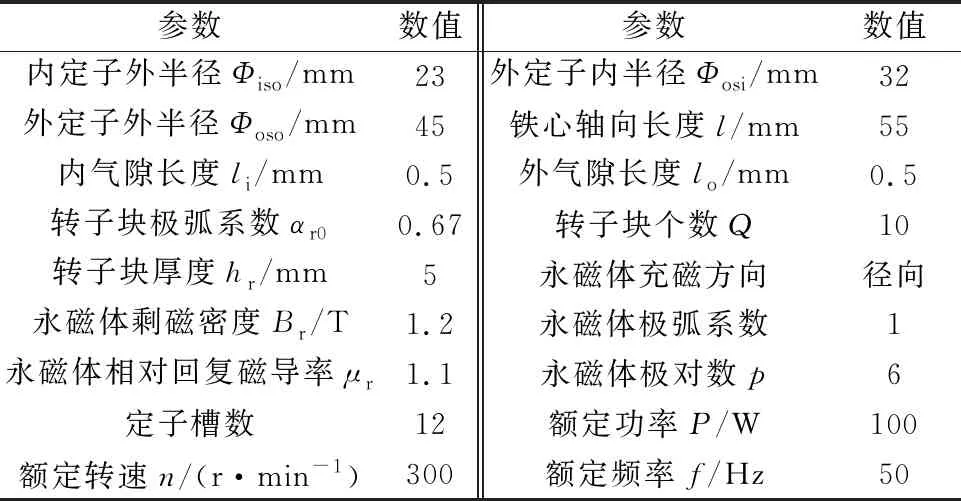
表1 傳統雙定子磁通反向電機樣機參數

圖4為某一時刻下，不同轉子下內、外層氣隙磁密的對比圖。通過圖4可以看出，在保證階梯形轉子外層階梯塊極弧系數和傳統轉子極弧系數相等，即αr3=αr0時，外層氣隙磁場基本沒有變化，說明此時階梯形轉子對外層氣隙磁場能量沒有影響；而內層磁場由于氣隙磁導改變，磁場發生了改變。

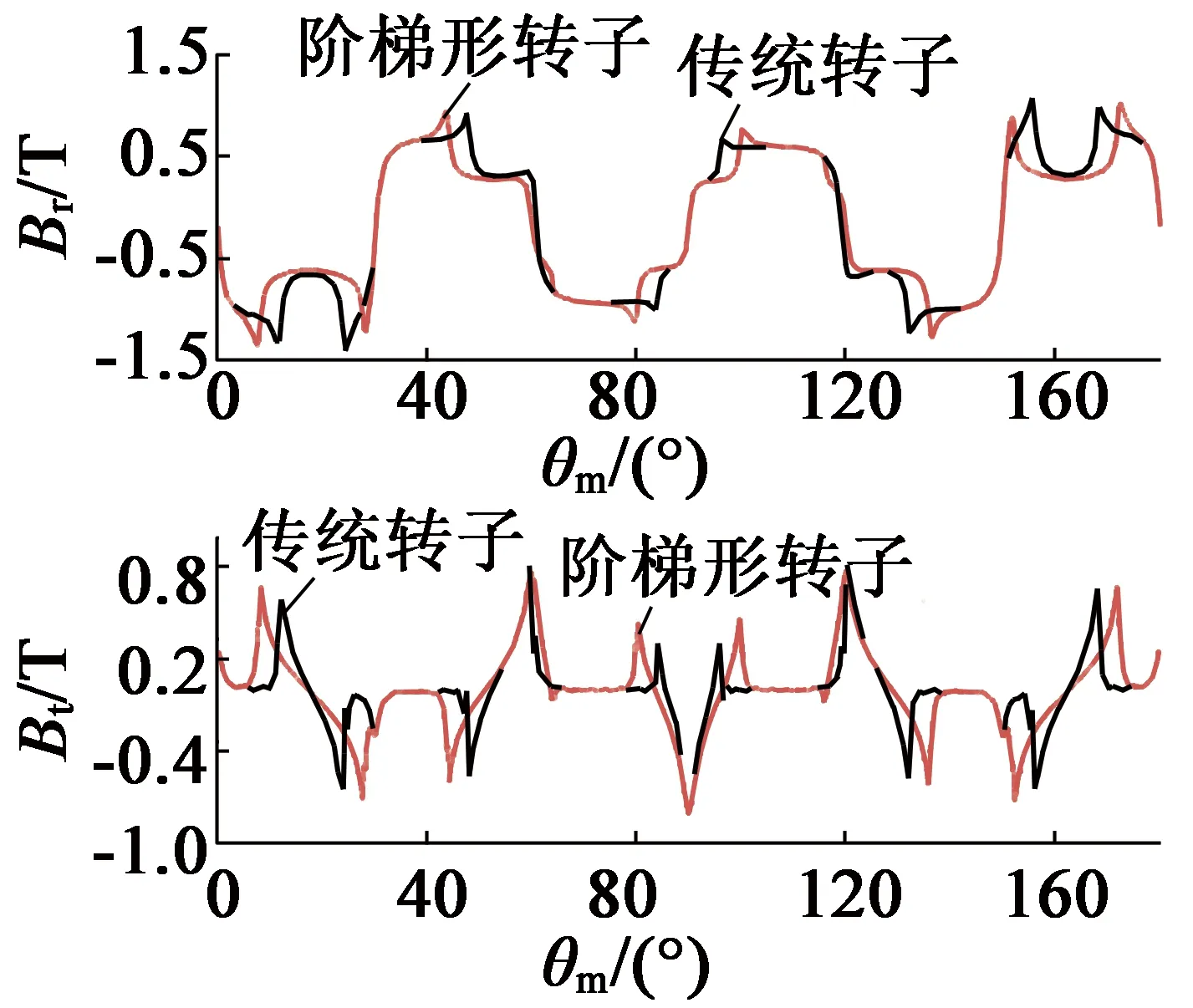
(a) 內氣隙磁場對比

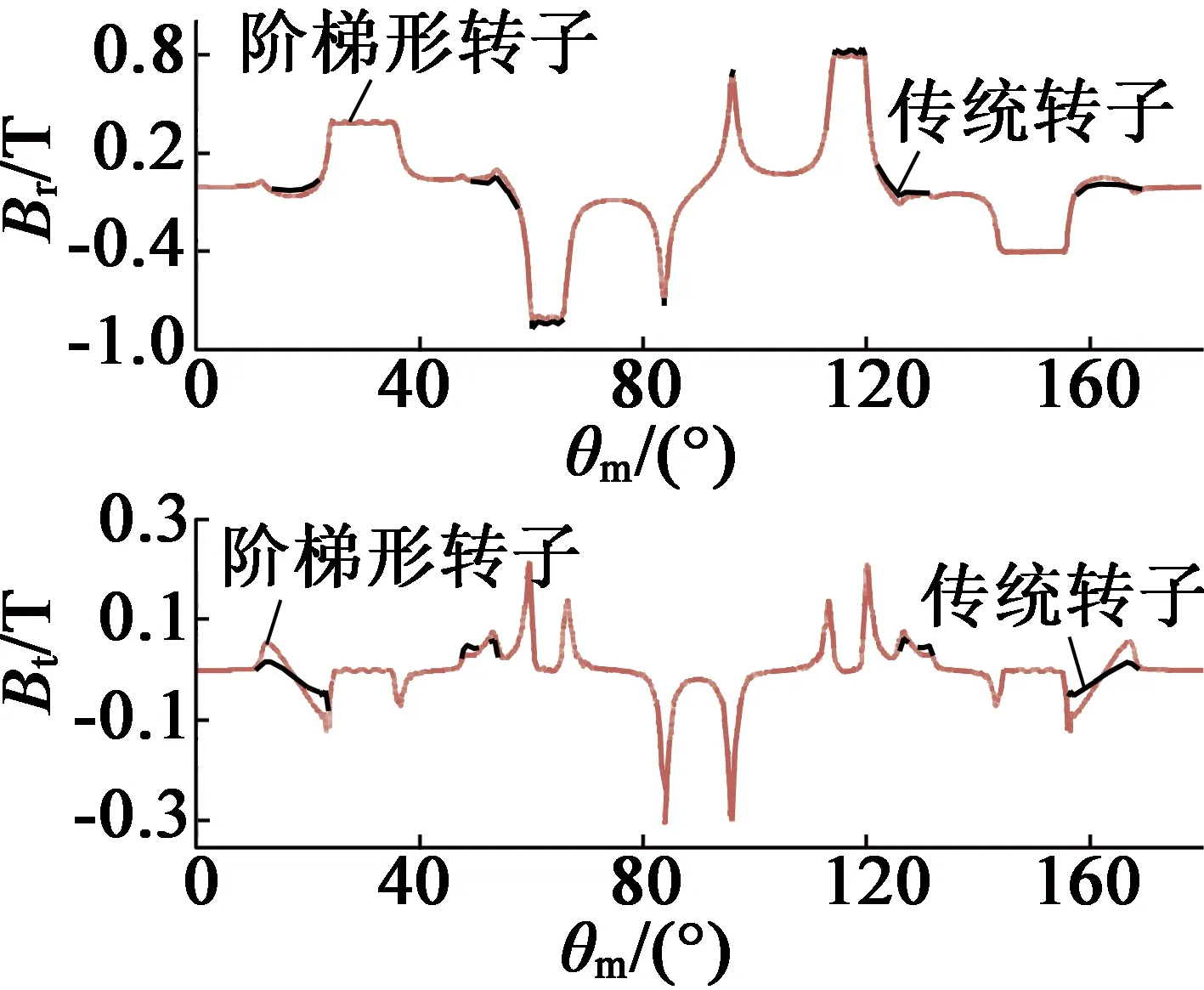
(b) 外氣隙磁場對比

圖5給出了不同轉子下齒槽轉矩的波形圖和諧波圖。可以看出，對于不同形狀的轉子，齒槽轉矩的周期都為機械角度6°，與上述分析一致，說明齒槽轉矩主要由內層磁場能量決定，證明了以上定性分析方法是合理的。通過對比兩個不同轉子的齒槽轉矩諧波可知，雙定子磁通反向電機的齒槽轉矩主要由前兩次諧波構成；傳統轉子電機的齒槽轉矩的幅值為439 mN·m,為額定轉矩的13.8%；而在階梯形轉子作用下，齒槽轉矩的幅值減小到200 mN·m,其主要原因是齒槽轉矩的基波幅值被大幅度削弱。說明使用階梯形轉子時能夠降低內層氣隙磁導幅值，從而降低齒槽轉矩的幅值。

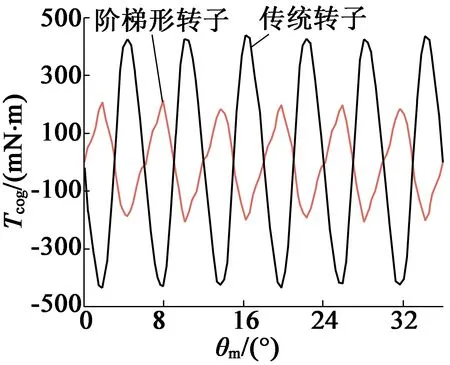
(a) 電機齒槽轉矩波形

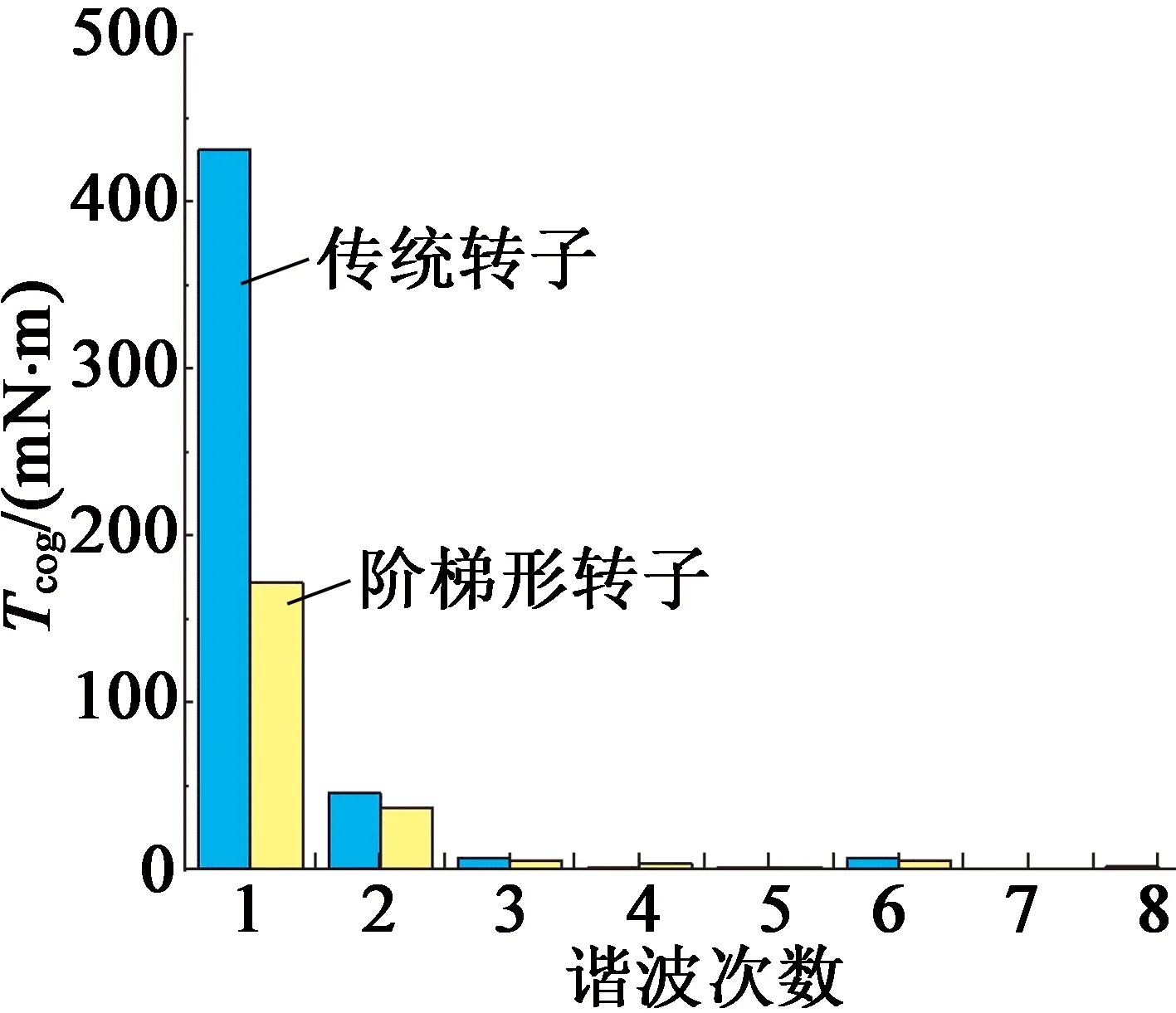
(b) 電機齒槽轉矩諧波圖

2 各層階梯極弧系數對電機性能的影響

基于上述分析可知，階梯形轉子能夠影響氣隙磁導從而改變齒槽轉矩的大小，針對三層階梯轉子，仍令h1=h2=h3=1.33 mm，保證階梯形轉子總厚度不變，研究各層轉子極弧系數對雙定子磁通反向電機齒槽轉矩和電磁性能的影響。

在電機其他參數不變的情況下，只改變各層階梯塊的極弧系數，在改變αri(i=1,2,3)時，保持αrj=0.67=αr0(j=1,2,3,j≠i)，這里取0.3<αri(i=1,2,3)<0.95。

2.1 各層階梯塊極弧系數對齒槽轉矩的影響

圖6為齒槽轉矩幅值隨各層階梯塊極弧系數的變化曲線。可以看出，只改變內層階梯塊極弧系數αr1時，齒槽轉矩幅值的波動較大，當αr1=0.41, 0.55, 0.73,0.89時對齒槽轉矩有較好抑制作用，其中當αr1=0.89時對齒槽轉矩的削弱程度最大，此時齒槽轉矩降低到33 mN·m,降低了92.5%；只改變中層階梯塊極弧系數αr2時，對齒槽轉矩的影響不是很大，只有當αr2>0.6時齒槽轉矩略減；只改變外層階梯塊極弧系數αr3時，對齒槽轉矩的影響也很大，當αr3=0.4,0.47時對齒槽轉矩的抑制效果較好，其中當αr3=0.4時齒槽轉矩的抑制效果最佳，此時齒槽轉矩降低到52 mN·m,降低了88%。

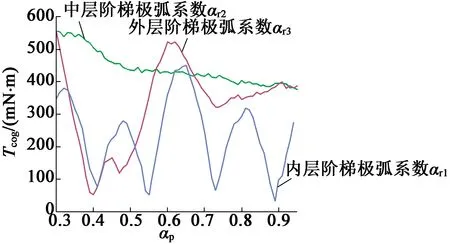
圖6 各層極弧系數對齒槽轉矩的影響

可見，當只改變一個階梯層的極弧系數時，內層和外層階梯塊對齒槽轉矩的抑制作用較強，合理選擇內層階梯塊和外層階梯塊的極弧系數時，能夠有效抑制齒槽轉矩；而中層階梯塊極弧系數αr2應大于0.6，否則起不到抑制齒槽轉矩的作用，反而會使齒槽轉矩進一步增大。

2.2 各層階梯塊極弧系數對反電動勢的影響

圖7給出了反電動勢基波幅值隨各層階梯塊極弧系數的變化曲線。可以看出，每層階梯塊對反電動勢基波幅值的影響都呈現出相同的規律，都是隨著極弧系數的增大先增后減。這是因為極弧系數很小時，通過轉子調制塊的磁通就少，從而與外定子電樞繞組匝鏈的磁通就少，因此反電動勢就低；隨著極弧系數的增大，通過轉子調制塊和外定子電樞繞組的磁通也隨之增加；而當極弧系數增加到一定程度時，相鄰的兩個轉子調制塊的距離就會減小，導致相鄰兩塊轉子調制塊的磁阻減小，此時，通過該塊轉子調制塊的磁通會有一部分流向相鄰的轉子調制塊，原本應該全部流向外定子的磁通被相鄰的轉子調制塊分流，從而增大了漏磁，減小了與外定子繞組匝鏈的磁通，使反電動勢再次減小。三層階梯塊中，反電動勢基波幅值隨外層階梯塊極弧系數αr3的變化幅度最大，當αr1,αr2,αr3的取值在0.67左右時，對反電動勢的影響不會很大。

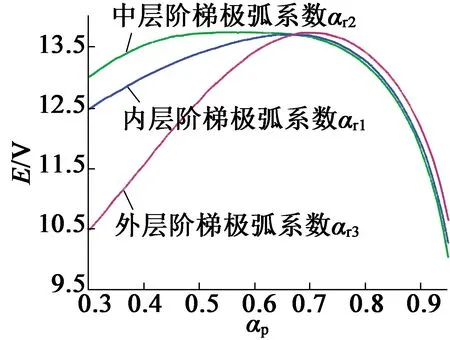
圖7 各層極弧系數對反電動勢基波幅值的影響

因此，在選擇極弧系數時，應使αr3稍大，否則反電動勢幅值會大幅度降低，影響電機出力，而αr1和αr2的選擇自由度相對較高。

圖8給出了反電動勢諧波含量隨各層階梯塊極弧系數的變化曲線。可以看出，內層階梯塊極弧系數αr1對反電動勢諧波含量的影響很小，隨著αr1的增大，反電動勢的諧波含量都保持在4%左右；中層階梯塊極弧系數αr2對反電動勢諧含量的影響較大，隨著αr2的增大而減小；而外層階梯塊極弧系數αr3對反電勢諧波的影響則更加復雜，當αr3=0.86時，反電動勢諧波降低到1%。

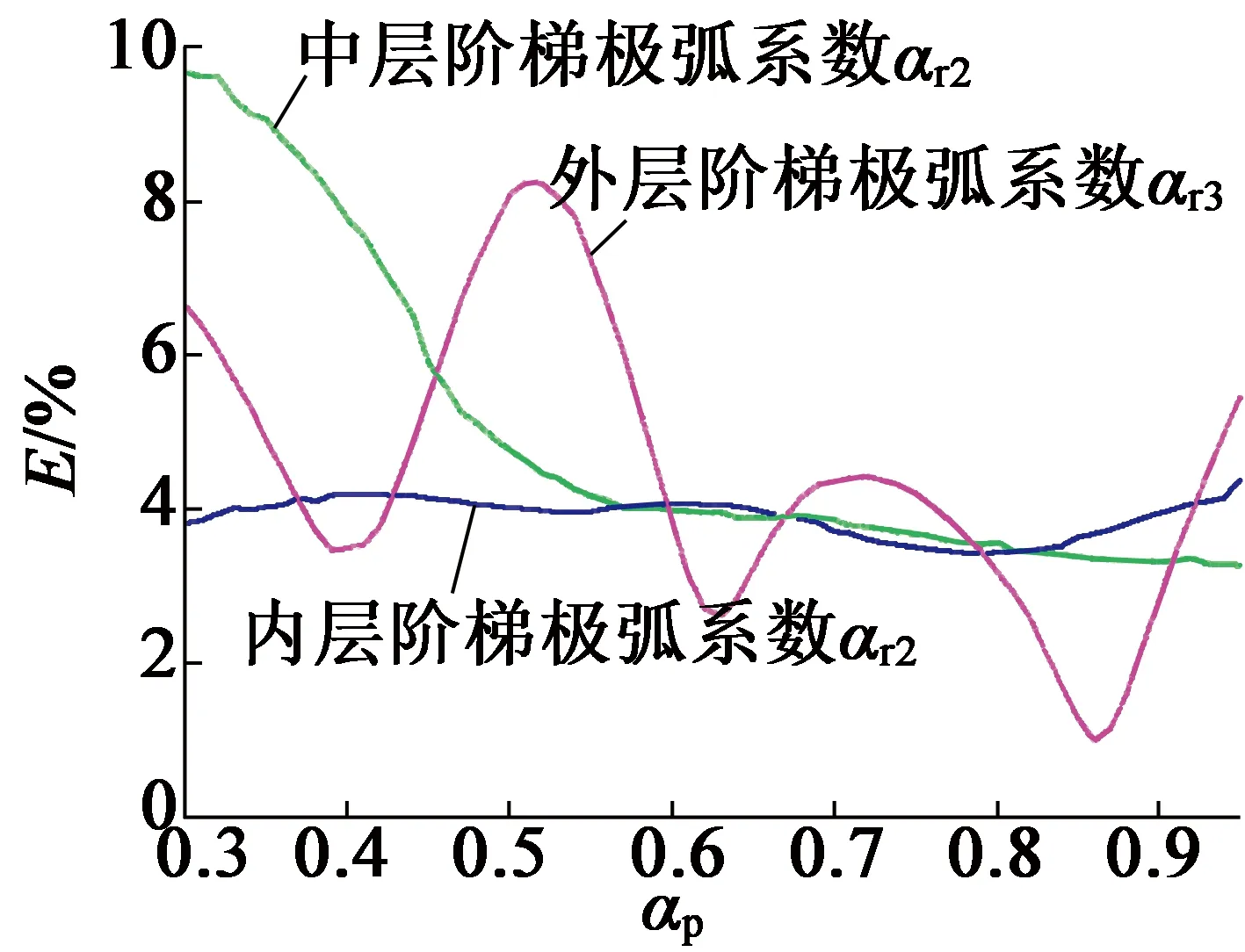
圖8 各層極弧系數對反電動勢諧波幅值的影響

因此，要想降低反電動勢的諧波含量，αr2，αr3應大于0.6，αr1的選擇自由度較高。

綜上可知，采用三層等厚的階梯形轉子時，單一改變內、外層階梯塊的極弧系數能夠有效地削弱齒槽轉矩，與此同時，反電動勢的變化也比較大，這將影響到電機負載時的輸出轉矩大小和轉矩波動程度。因此，必須結合全局優化方法和有限元方法來獲得使電機性能最好時的各層階梯塊的參數。

3 遺傳算法優化設計

3.1 遺傳算法

遺傳算法是一類基于生物界自然選擇的進化規律演化而來的搜索優化方法。相較于傳統算法，遺傳算法具有較強的魯棒性，對目標函數不作連續性要求，具有全局優化的特點[19]。遺傳算法的基本原理是適者生存，優勝劣汰。求解過程中采用適應度函數來評價種群中每個個體的適應度，一方面采用每代最優個體進行迭代，另一方面又按照自然界基因的交叉和變異來產生新的個體，經過若干次種群的迭代逐步去尋找最優的參數組合[20]。遺傳算法的基本流程如圖9所示。

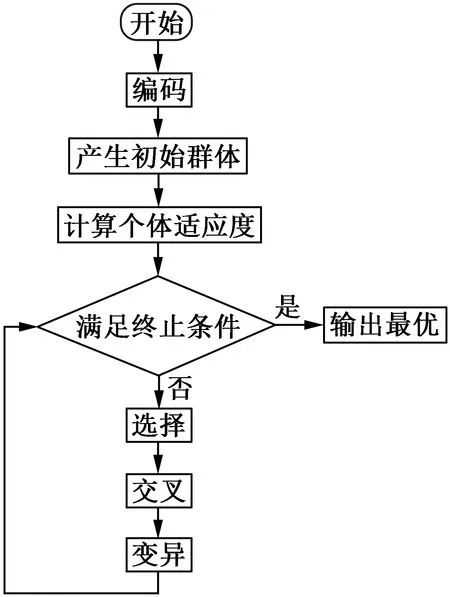
圖9 遺傳算法流程圖

3.2 目標函數的選取

目標函數的建立是電機全局優化過程中最重要的步驟之一，合理的目標函數對實際優化效果有著決定性的作用，一方面要確定正確的優化方向，另一方面也要考慮電機設計的實際需求。對于雙定子磁通反向電機，一方面要求齒槽轉矩小，另一方面又希望反電動勢基波幅值大，正弦度高。本文將需要優化的多個目標函數通過加權方式，轉化為單目標優化，設定目標函數：

式中：Tcog為齒槽轉矩幅值；THDemf為反電勢諧波含量；E1為反電動勢基波幅值。

3.3 優化變量的選取

基于上文的分析，可以看出，內層階梯塊極弧系數αr1的選擇自由度較高，而中層、外層階梯塊的極弧系數αr2和αr3應大于0.6，否則會影響反電動勢諧波含量和基波幅值；同時，上文并未分析各層階梯塊厚度對電機性能的影響。在這里采用全局優化的方法來研究各層階梯塊極弧系數和厚度對雙定子磁通反向電機綜合性能的影響。

選取αr1,αr2,αr3,h1,h2,h3作為優化變量，并保證階梯形轉子總厚度不變，綜合考慮之下，各變量的取值范圍及約束條件:

3.4 優化算法的實現

取交叉概率Pc=0.65，變異概率Pb=0.1，種群數量NP=80，迭代次數G=100進行優化，使目標函數最小。可得遺傳算法的迭代進化圖如圖10所示。

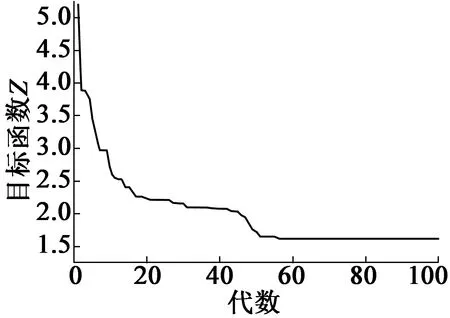
圖10 遺傳算法迭代進化圖

其最優解αr1=0.36，αr2=0.84，αr3=0.87，h1=0.36 mm，h2=2.48 mm，h3=2.16 mm。

圖11為階梯形轉子優化后齒槽轉矩和傳統轉子齒槽轉矩對比圖。可以看出，優化后的齒槽轉矩從439 mN·m降低為19 mN·m，降低了95.7%，相對于原電機模型齒槽轉矩削弱效果顯著。

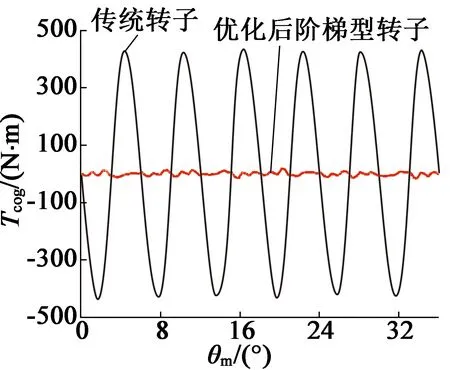
圖11 傳統轉子和優化階梯形轉子齒槽轉矩波形比較

圖12為階梯形轉子優化后與傳統轉子的反電動勢波形和諧波對比圖。比較可知，優化后的反電動勢基波從13.7 V降低到了11.7 V,降低了14.6%；但是反電動勢諧波含量從4%降低到了1%，更有助于提升負載時轉矩的平穩性。

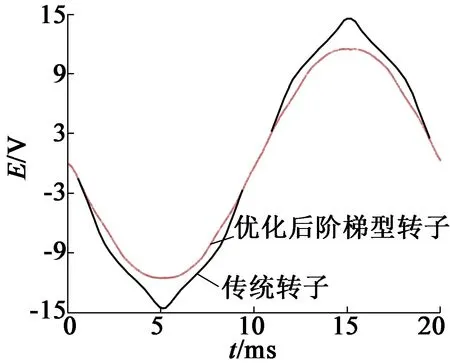
(a) 反電動勢波形比較

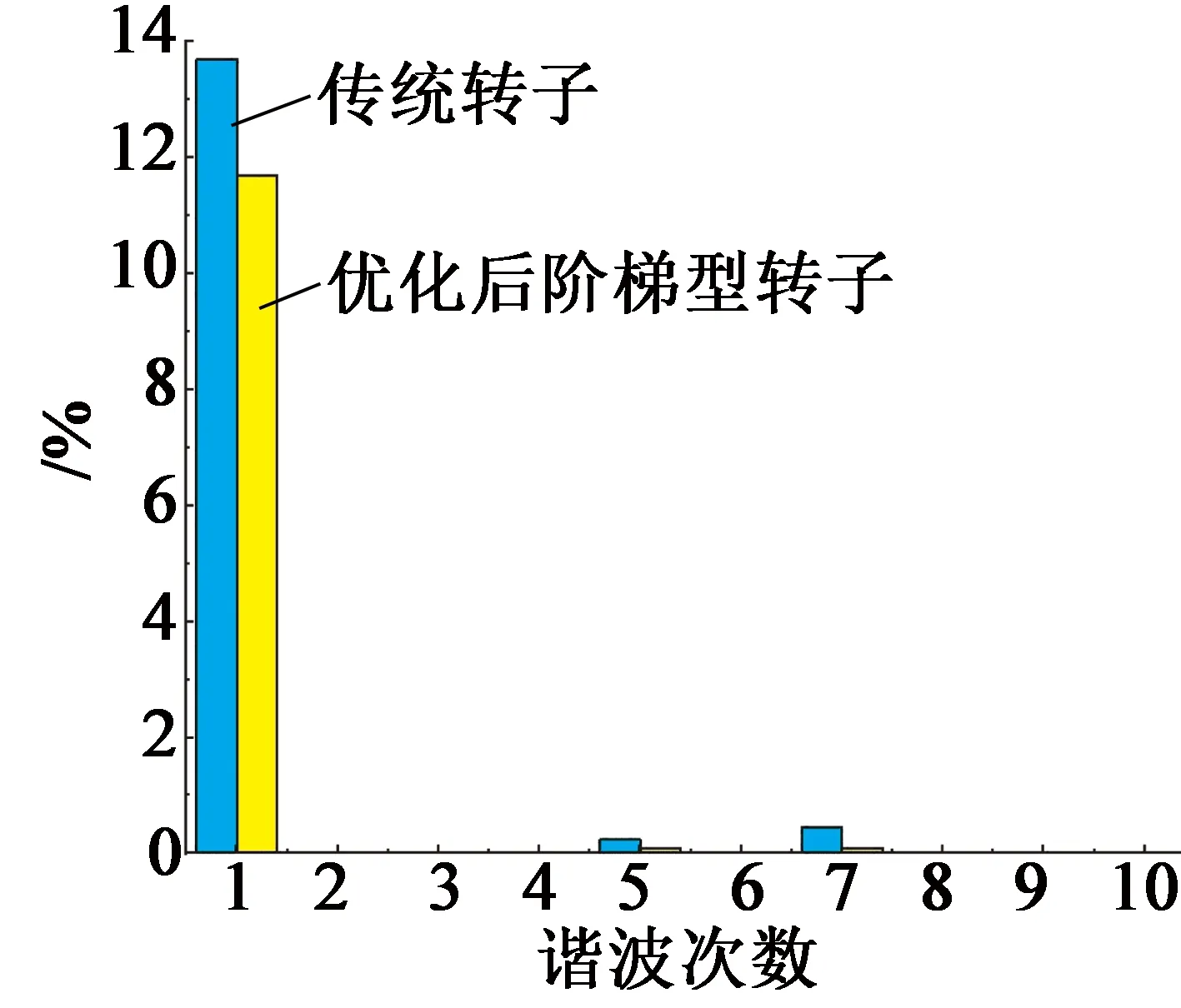
(b) 反電動勢諧波比較

3.5 優化前后負載性能對比

圖13給出了優化后的階梯形轉子和傳統轉子在通入三相正弦額定電流時的負載轉矩。可以看出，原電機負載平均轉矩為3.24 N·m,轉矩波動為32%；而采用階梯形轉子進行優化后的平均轉矩為2.77 N·m，轉矩波動為2.4%。對比可知，優化后平均轉矩雖然只降低了約14.5%，但是轉矩波動從32%降低到了2.4%。階梯形轉子在犧牲一部分輸出轉矩的情況下能夠大幅度地削弱轉矩脈動，提升轉矩的平穩性。

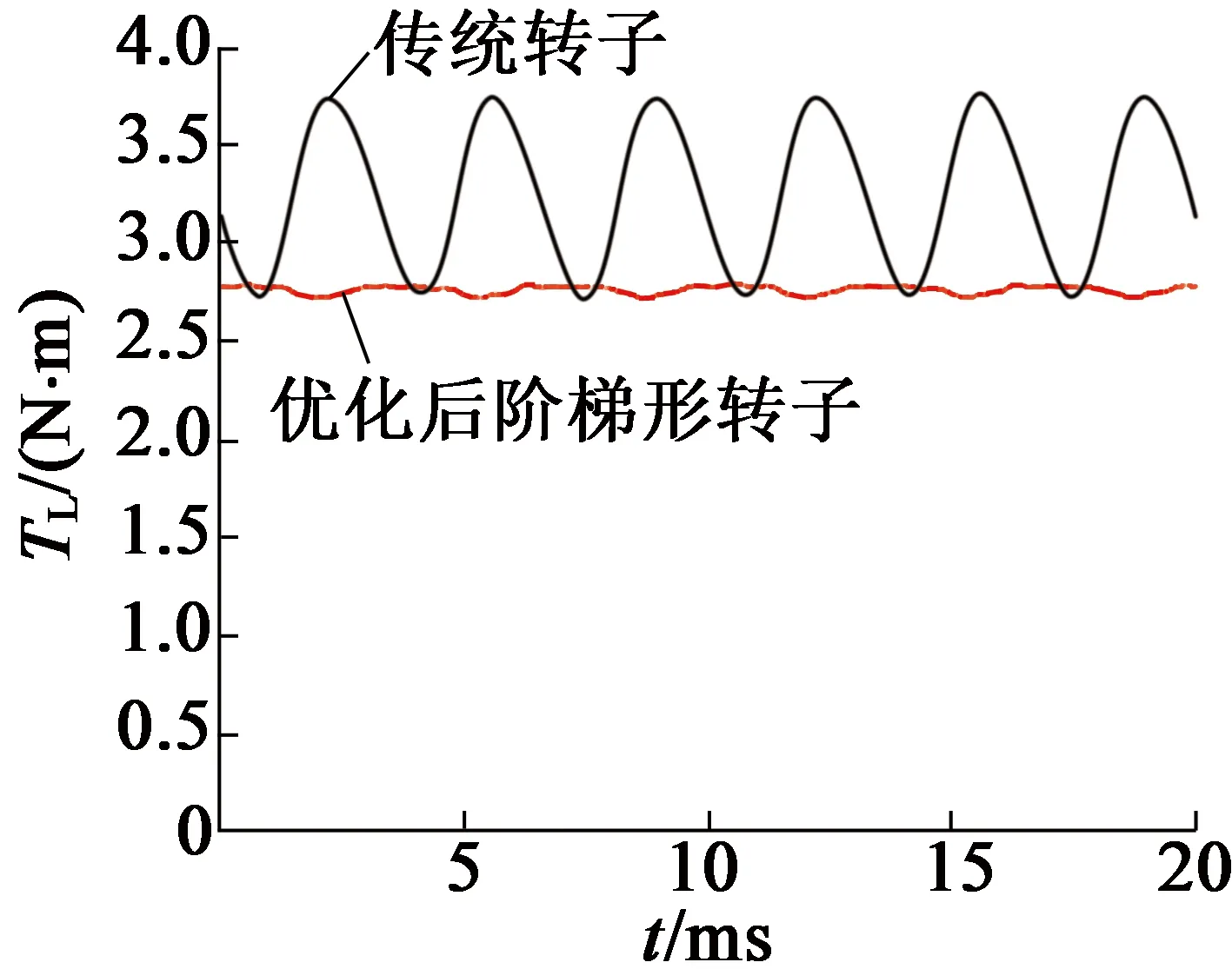
圖13 傳統轉子與階梯形轉子的負載轉矩比較

4 結 語

為了降低雙定子磁通反向電機的齒槽轉矩，本文采用階梯形轉子來代替傳統轉子，以12/10極的雙定子磁通反向電機為研究對象，研究了不同層階梯塊極弧系數對電機齒槽轉矩和電機性能的影響。

研究結果表明，不同層階梯塊的極弧系數對雙定子磁通反向電機的齒槽轉矩和反電動勢的影響不同。其中內、外層階梯塊的極弧系數對齒槽轉矩的影響很大；中、外層階梯塊的極弧系數對反電動勢諧波含量和基波幅值的影響很大。在保證階梯形轉子總厚度不變的情況下，采用遺傳算法對不同層階梯塊的極弧系數和厚度進行綜合優化得到最優解，不僅極大程度地削弱了齒槽轉矩，還提高了反電動勢的正弦度以及負載時的電磁轉矩平穩度。在空載下，齒槽轉矩降低了95.7%；在額定負載下，轉矩波動從32%下降到2.4%，而平均轉矩僅下降了14.5%，證明了該方法的有效性。