數學應用題的常見類型及其解法

山東 秦 振

數學應用題是指用數學的思想方法將一個表面上非數學問題或非完全的數學問題轉化為完全數學形式化的問題.應用題的內容十分廣泛，解題方法靈活，難度較大、能力要求較高.解應用題需要在陌生的情景中理解、分析所給的問題，并能通過題目中提供的信息，利用化歸與轉化的數學思想方法將實際問題轉化為相應的數學問題，然后選擇適當的數學方法解決問題.

解決應用題的思路方法：一是要認真仔細地分析問題，弄清題意，理清問題中的已知條件以及要求解的結論，分清題目中的已知量和未知量及它們之間的關系；二是用數學語言表達實際問題中的相關信息，將實際問題轉化為我們熟悉的數學問題——即數學建模；三是將得到的數學模型轉化為“常規”的數學問題，然后根據問題的特點選擇適當的數學思想方法和解題技巧解決問題，得到相應的結果；四是對得到的結果進行檢驗，做出解釋或預測，給出答案.

下面結合例題介紹應用題的常見類型及其解法.

一、函數的應用

函數知識內容豐富，在現實生活中應用廣泛，諸如我們經常遇到的成本最低、利潤最高、產出最大、用料最省、效益最大等應用問題，通常可以先轉化為函數問題，再利用函數的性質解決.

【例1】如果你有一筆資金用于投資，現在有三種方案供你選擇，這三種方案的回報如下：

方案一：每天回報40元；

方案二：第一天回報10元，以后每天比前一天多回報10元；

方案三：第一天回報0.4元，以后每天的回報比前一天翻一番.

請問，你會選擇哪種投資方案？

【分析】先根據題意建立三種投資方案對應的函數模型，再比較它們的增長情況，為選擇投資方案提供依據.

解:設第x天所得回報是y元，根據題意，可得

方案一:可以用函數f1(x)=40(x∈R+)進行描述；

方案二:可以用函數f2(x)=10x(x∈R+)進行描述；

方案三:可以用函數f3(x)=0.4×2x-1(x∈R+)進行描述.

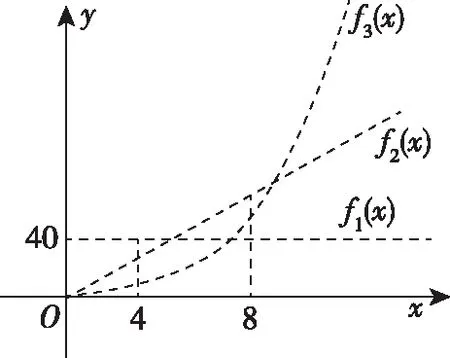
在同一坐標系分別作出這三個函數圖象，如圖所示.

由圖象可知，每天所得回報，在1～4天，方案一最多，在第5～8天，方案二最多，第9天開始，方案三最多.

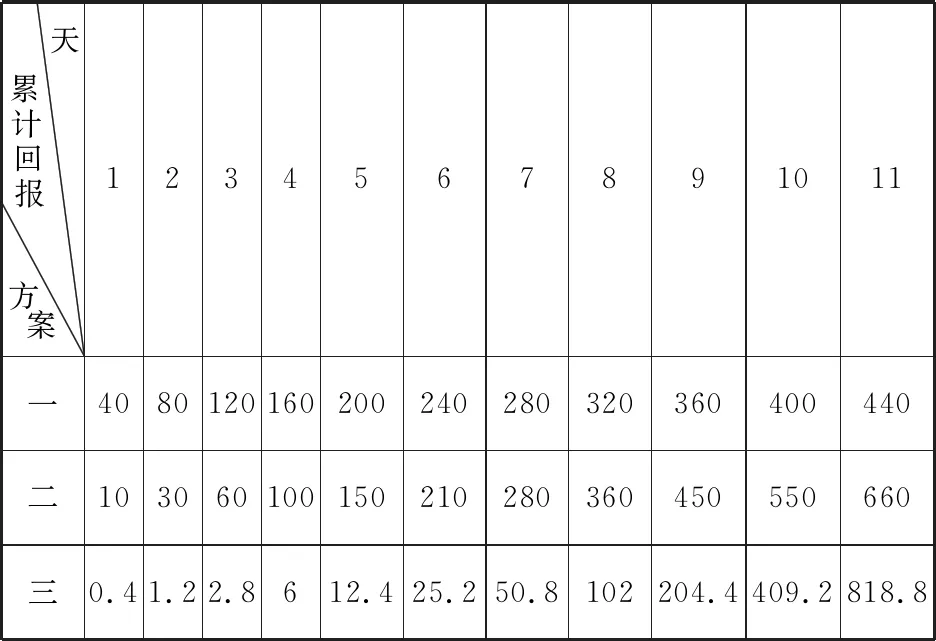
天累計回報方案1234567891011一4080120160200240280320360400440二103060100150210280360450550660三0.41.22.8612.425.250.8102204.4409.2818.8

再看累計回報數，如上表所示，投資7天以下(不含7天)，應選擇第一種投資方案；投資7天，選擇第一、二種方案均可；投資8～10天，應選擇第二種方案；投資11天(含11天)以上，則應選擇第三種投資方案.

【評注】通過建立相應的目標函數，確定變量的限制條件，利用函數圖象、函數變量表以及函數性質，是解決函數型應用問題的基本方法.

二、不等式(組)的應用

數學知識之間的轉化基本上就是等量轉化和不等關系轉化，因此在求某些量的范圍或最值時，一般要建立不等式模型.

【例2】建筑學規定，民用住宅的窗戶面積必須小于地板面積，但按采光標準，窗戶面積與地板面積的比不應小于10%，并且這個比越大，住宅的采光條件越好.問同時增加相等的窗戶面積和地板面積，住宅的采光條件是變好了，還是變壞了？請說明理由.

【分析】要確定住宅的采光條件是變好了，還是變壞了，就是要比較原來窗戶面積和地板面積的比值與窗戶面積和地板面積增加以后的比值誰大、誰小.若是原來的面積比值大，則采光條件變壞了；如果是增加了面積以后的窗戶面積和地板面積的比值大，則采光條件變好了.

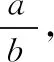
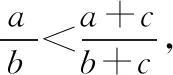
【評注】本題告訴我們，采光條件的好壞由窗戶面積與地板面積比值的大小來衡量，并且是這個比值越大，采光條件越好，但是要注意建筑學的規定：這個比值應小于1.

三、數列的應用

我們熟悉的增長率、存款利息、分期付款、期貨貿易、人口增長等實際問題通常可以轉化為數列問題，利用數列的有關性質解決.

【例3】學習數學可以使我們更聰明，思維更加縝密.在美國廣為流傳的一道數學題是：老板給你兩種加工資的方案：一是每年增加薪水1 000元；二是每半年增加300元，請選一種.一般不擅長數學的，很容易選擇前者.因為一年加1 000元總比兩個半年共加600元要多.其實，由于加工資是累計的，時間越長，第二種方案往往更有利.例如在第二年的年末，根據第一種方案可以加得1 000+2 000=3 000(元)，而第二種方案第一年加得300+600=900(元)，第二年加得900+1 200=2 100(元).但是到了第三年，第一方案加得1 000+2 000+3 000=6 000(元)，第二方案加得300+600+900+1 200+1 500+1 800=6 300(元)，比方案一多了300元.第四年、第五年會更多，因此，你若能在該公司工作三年以上，則應該選擇第二方案.

根據以上資料，解答下列問題：

(1)如果在該公司工作10年，選擇第二方案比第一方案多加薪多少元？

(2)若第二方案改成每半年增加a元，問a為何值時，選擇第二方案總是比第一方案多加薪？

【分析】(1)分別計算出兩種加薪方案的加薪數額，然后比較.(2)根據題目提供的信息，分別寫出第n年末兩種方案的加薪數，再根據題意轉化為不等式問題解決.

解：(1)在第10年末，由第一方案，得1 000+2 000+3 000+…+10 000=55 000(元).由第二方案，得(300+300×2)+(300×3+300×4)+…+(300×19+300×20)=63 000(元).因為63 000-55 000=8 000(元)，所以在該公司工作10年，選擇第二方案比第一方案多加薪8 000元.

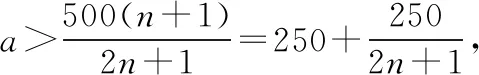
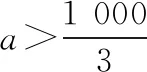
【評注】實際問題轉化為不等式問題后，往往要結合函數的性質及不等式的性質解決.

四、導數的應用

導數是高中數學的重要內容之一，是解決最優、最大、最小和比較大小等應用問題的有力工具.應用導數解決實際問題的方法是首先建立函數模型，寫出函數關系y=f(x)；求出函數的導數f′(x)，解方程f′(x)=0，求出極值點；比較函數在區間端點的函數值的大小，然后確定其最值，給出答案.

【例4】某市環保局調查了該市水泥廠的污染情況.調查發現，水泥廠的煙囪向周圍地區散落煙塵造成環境污染.已知A，B兩座水泥廠煙囪相距20 km，其中B煙囪噴出的煙塵是A煙囪的8倍.經環境監測表明：落在地面某處的煙塵濃度與該處到煙囪距離的平方成反比，而與煙囪噴出的煙塵量成正比(比例系數均為k).若C是A，B連線上的點，設AC=xkm，C點的煙塵濃度記為y.

(1)寫出y與x的函數表達式；

(2)是否存在這樣的點C，使該點的煙塵濃度最低？若存在，求出A，C兩地的距離；若不存在，請說明理由.

【分析】(1)由AC=x，可得BC=20-x.根據“落在地面某處的煙塵濃度與該處到煙囪距離的平方成反比，而與煙囪噴出的煙塵量成正比(比例系數均為k).”可得函數表達式.(2)利用導數法討論函數的最小值.

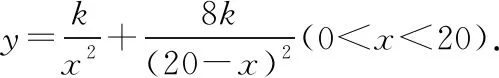
【評注】應用導數法解決實際問題，首先要根據題意確定自變量的取值范圍，注意極大值與最大值的關系，還要驗證函數在區間端點所對應的函數值的大小.

五、三角函數的應用

有些涉及幾何圖形、角度、航海、測量等方面的問題，可以轉化為三角函數問題，利用三角函數的性質解決.

【例5】某監控室的工作人員，主要是根據儀表的數據變化加以操作控制的，若儀表高m米，底邊距地面n米，如圖所示，工作人員坐在椅子上眼睛距地面的高度為1.2米(n>1.2)，問工作人員坐在什么位置看得最清楚？

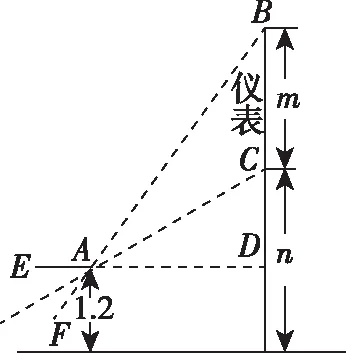
【分析】工作人員觀察儀表看得最清楚的位置，就是使∠BAC達到最大時點A的位置.由于∠BAC是銳角，因此要使它最大，可以轉化為該角的正切最大，即tan∠BAC最大.

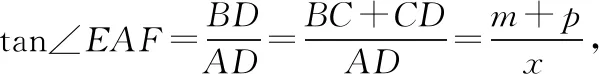
【評注】三角函數在測距、測角等方面的應用比較廣泛，也是最常見的問題.在解決此類應用問題時，應熟悉視角、方位角、仰角、俯角等概念，并能熟練應用三角函數的性質解決有關問題.另外，可以研究在家看電視時，坐在什么位置看得最清楚.

六、線性規劃的應用

在生活實踐中，經常遇到給定人力、物力、財力資源，讓我們應用這些資源，獲得最大效益；或者給定一項任務，完成任務的人力、物力、財力最小.這些實際問題往往需要應用線性規劃解決.

【例6】某營養師要為某個兒童預定午餐和晚餐.已知一個單位的午餐含12個單位的碳水化合物，6個單位的蛋白質和6個單位的維生素C；一個單位的晚餐含8個單位的碳水化合物，6個單位的蛋白質和10個單位的維生素C.另外，該兒童這兩餐需要的營養中至少含64個單位的碳水化合物，42個單位的蛋白質和54個單位的維生素C.如果一個單位的午餐、晚餐的費用分別是2.5元和4元，那么要滿足上述的營養要求，并且花費最少，應當為該兒童分別預定多少個單位的午餐和晚餐？

【分析】根據題意設出相關變量建立線性約束條件、目標函數，利用線性規劃的有關知識，作出可行域，找出最優解，再還原為實際問題.

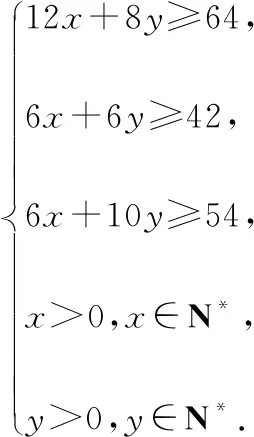
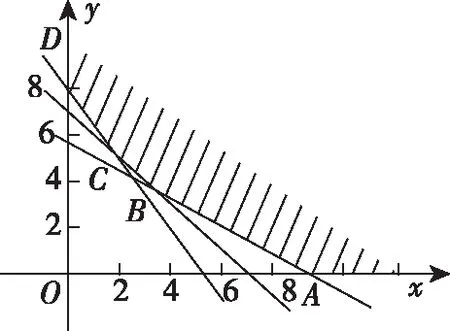
【評注】線性規劃的最優解往往取在邊界直線的交點處，另外，解決這類問題的易錯點是在列約束條件時漏掉x>0，y>0，且它們都是正整數.

七、解析幾何的應用

這類問題通常涉及橋梁、隧道、反光燈、通風塔、人造衛星運行軌跡等實際問題.解決這類問題的方法是首先弄清題意，建立合理的坐標系，將等量關系轉化為相應的方程(組)，研究曲線方程得到結論.

【例7】為了在神舟六號飛船返回艙順利到達地球后及時將航天員安全救出，地面指揮中心在返回艙預計到達區域安排三個救援中心(記為A，B，C)，A在B的正東方向，相距6千米，C在B的北偏西30°方向，相距4千米，P為航天員著陸點，某一時刻，A接收到P的求救信號，由于B，C兩地比A距P遠，因此4秒后，B，C兩個救援中心才同時接收到這一信號.已知該信號的傳播速度為1千米/秒.

(1)求在A處發現P的方位角；

(2)若信號從P點的正上空Q點處發出，則A，B收到信號時間差變大還是變小？說明理由.

【分析】根據題意，利用“某一時刻，A接收到P的求救信號，由于B，C兩地比A距P遠，因此4秒后，B，C兩個救援中心才同時接收到這一信號”轉化為方程，構建解析幾何模型解決.

解：(1)因為|PC|=|PB|，所以P點在線段BC的垂直平分線上，又因為|PB|-|PA|=4，所以P點在以A，B為焦點的雙曲線的右支上.以線段AB中點為原點，AB所在直線為x軸建立直角坐標系，如圖所示，

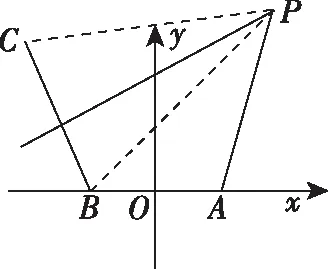
(2)如圖所示，

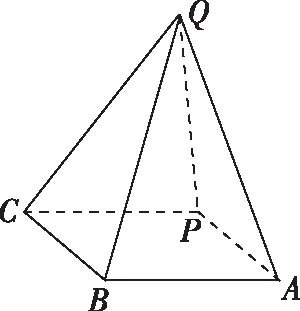
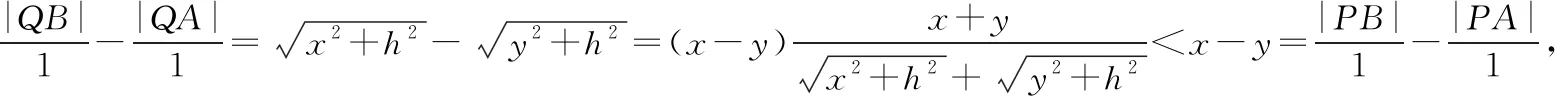
【評注】由于B，C兩地比A地接收到的信號慢4秒，即|PB|-|PA|=4，滿足雙曲線的定義，據此建立雙曲線模型，使實際問題轉化為解析幾何問題.這類問題在建立數學模型時，要分清物體的運動形式和曲線的形狀符合哪一種圓錐曲線的定義或圖形，再根據題意轉化為相應的曲線方程.

八、立體幾何的應用

在工作、生活中經常遇到空中觀測、地球的經緯度等實際背景下幾何體的截面積、表面積和體積的計算，以及空間位置關系的確定等問題，這些實際問題一般都能利用立體幾何模型解決.

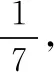
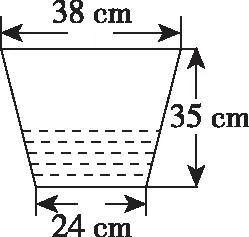
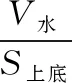
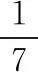
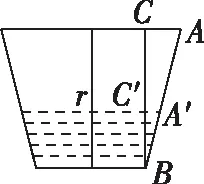
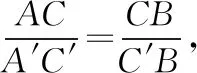
【評注】在解決幾何體問題中，所給“數據”一般要轉化到一個三角形中，因此特征三角形的構建是解題的重點，而構建特征三角形一般從幾何體的高及斜高入手，如本題中的△ABC.另外，本題在求出體積后，因為所求的“降雨的降水量”要用到水的體積的不變性，因此根據題意把臺體轉化為柱體，進而求出降水量.

九、概率統計的應用

這類問題的背景可以是當前的社會熱點問題，也可以是某些“常規”問題，其特點是需要用概率與統計的基礎知識和基本方法解決.解決此類問題的方法是分析問題的要求，弄清題意，建立相應的統計與概率模型，然后選擇適當的方法和性質解決.

【例9】工作人員需要進入核電站完成某項具有高輻射危險的任務，每次只派一個人進去，且每個人只派一次，工作時間不超過10分鐘.如果前一個人10分鐘內不能完成任務則撤出，再派下一個人.現在一共只有甲、乙、丙三個人可派，他們各自能完成任務的概率分別為p1，p2，p3，假設p1，p2，p3互不相等，且假定各人能完成任務的事件相互獨立.

(1)如果按甲最先、乙次之、丙最后的順序派人，求任務能被完成的概率.若改變三個人被派出的先后順序，任務能被完成的概率是否發生變化？

(2)若按某指定順序派人，這三個人各自能完成任務的概率依次為q1，q2，q3，其中q1，q2，q3是p1，p2，p3的一個排列，求所需派出人員數目X的分布列和均值(數學期望)E(X).

(3)假定1>p1>p2>p3，試分析以怎樣的先后順序派出人員，可使所需派出的人員數目的均值(數學期望)最小.

【分析】(1)直接計算比較復雜，可以考慮問題的“反面”；(2)根據題意列出隨機變量X的分布列，再利用公式計算E(X)；(3)根據“經驗”，優先派出完成任務概率大的人，可減少所需派出的人員數目的均值；然后證明.

解：(1)無論以怎樣的順序派出人員，任務不能完成的概率都是(1-p1)(1-p2)(1-p3)，所以任務能完成的概率與三個人被派出的先后順序無關，并等于1-(1-p1)(1-p2)(1-p3)=p1+p2+p3-p1p2-p2p3-p3p1+p1p2p3.

(2)當依次派出的三個人各自完成任務的概率分別為q1，q2，q3時，隨機變量X的分布列為

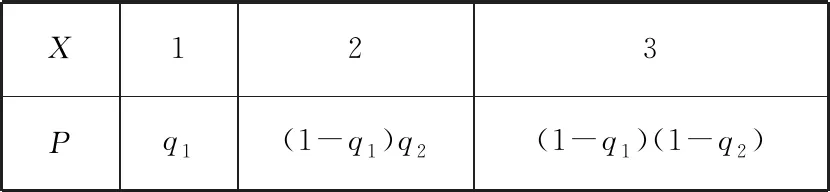
X123Pq1(1-q1)q2(1-q1)(1-q2)

所需派出的人員數目的均值(數學期望)是E(X)=q1+2(1-q1)q2+3(1-q1)(1-q2)=3-2q1-q2+q1q2.

(3)由(2)的結論可知，按甲最先、乙次之、丙最后的順序派人時，E(X)=3-2p1-p2+p1p2.根據經驗，優先派出完成任務概率大的人，可減少所需派出的人員數目的均值.下面證明：對于p1,p2,p3的任意排列q1,q2,q3，都有3-2q1-q2+q1q2≥3-2p1-p2+p1p2.

因為(3-2q1-q2+q1q2)-(3-2p1-p2+p1p2)=2(p1-q1)+(p2-q2)-p1p2+q1q2=2(p1-q1)+(p2-q2)-(p1-q1)p2-q1(p2-q2)=(2-p2)(p1-q1)+(1-q1)(p2-q2)≥(1-q1)[(p1+p2)-(q1+q2)]≥0，所以不等式成立.

因此當(q1,q2,q3)=(p1,p2,p3)時，E(X)得到最小，即完成任務概率大的人優先派出，可減小所需派出人員數目的均值.

【評注】此題考查了相互獨立事件的概率計算，離散型隨機變量及其分布列，均值等基本知識，同時考查了在現實生活中處理問題的能力以及抽象歸納能力、合情推理與演繹推理能力，還考查了數學化歸與轉化思想和分類討論思想.