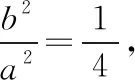極限論視角下客觀題的優化求解
浙江 丁揚愷
高三的考試題都是命題專家匠心獨運之作,尤其是選擇、填空小題部分,其方法多樣、思想靈活,具有鮮明的導向性,備受一線教師青睞.但由于壓軸小題難度大,如按照參考答案給學生解惑,會讓很多學生知其然,卻不知其所以然.其次在考場實戰限時條件下,大部分考生如達不到試題的高度則很難系統地運用通法求解,導致半途而廢,從而因考試對數學失去信心.鑒于此,筆者選取一些模擬考及高考試題,雖引入大學數學極限論思想,但本質是雙參數、雙動點的最佳逼近或是空間幾何體的極端值處理理論,再結合自己的教學體會,談談選擇壓軸小題的“優化運算”.
一、不等式視角
【例1】(2019·4月浙江學考·17)已知a,b,c,d是四個互不相等的正實數,滿足a+b>c+d且|a-b|<|c-d|,則下列選項正確的是
( )
A.a2+b2>c2+d2
B.|a2-b2|>|c2-d2|
思路:觀察題目中的兩個條件,|a-b|<|c-d|使得a,b間的差距小于c,d間的差距,可取a=6,b=5,c=2,d=4,排除B,C選項;考慮到選項A中數的平方性,可將d放大為8,排除A選項,故選D.
點評:該題正確答案D為條件|a-b|<|c-d|的細化,事實上出題者安排此題是讓學生用特殊值來排除選項,學生總是選擇一些無規律特值去代入,但排除的效果不明顯,如能抓住題干機理再讓個別數充分貼近或趨向無窮遠,則排除效果明顯,我們可以再來看下列數的有界性.
【例2】(2016·浙江卷理·8)已知實數a,b,c.
( )
A.若|a2+b+c|+|a+b2+c|≤1,則a2+b2+c2<100
B.若|a2+b+c|+|a2+b-c|≤1,則a2+b2+c2<100
C.若|a+b+c2|+|a+b-c2|≤1,則a2+b2+c2<100
D.若|a2+b+c|+|a+b2-c|≤1,則a2+b2+c2<100
思路:對A選項,觀察到a2+b,a+b2與c和的絕對值的零點,可取a=1,b=1,c=-2,能推出a2+b2+c2<100,然后我們將實數a,b,c放大,取a=100,b=100,c=-10 100得出矛盾;
同理對于B選項,a2+b為共性,可取a=1,b=-1,c=0,能推出a2+b2+c2<100,然后我們將實數a,b放大,取a=100,b=-10 000,c=0得出矛盾;
同理對于C選項,a+b為共性,可放大a,b,取a=100,b=-100,c=0得出矛盾.不難得出正確選項為D,對于D選項,|a2+b+c|+|a+b2-c|≤1表示a2+b到-c的距離與a+b2到c的距離之和小于等于1,因為a,b有界,則a2+b,a+b2都有界,故c有界,則a2+b2+c2有界.
點評:此題為2016年浙江卷選擇最后一題,考生在考場中如能先取部分滿足條件的特殊值,再趨向于無窮遠,則該道選擇壓軸題不難得出正確答案.
二、動態立體幾何視角
【例3】(2020·紹興一模·8)如圖,三棱錐V-ABC的底面ABC是正三角形,側棱長均相等,P是棱VA上的點(不含端點),記直線PB與直線AC所成角為α,二面角P-AC-B的平面角為β,則α+β不可能是
( )
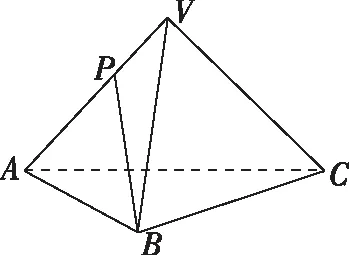
點評:該題是極限思想運用到立體幾何中,將三棱錐趨向于無窮小,則角的范圍迎刃而解.
【例4】(2019·浙大附中高三數學第二學期·9)如圖,已知△ABC中,AC>AB,AD是∠BAC的平分線,將△ABD沿直線AD翻折成△ADB1,在翻折過程中,設所成二面角B1-AD-C的平面角為α,∠B1AC=β,∠B1DC=γ,則下列結論中成立的是
( )
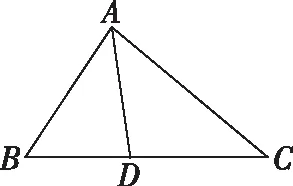
A.α≥β,α≥γB.α≥β,α≤γ
C.α≤β,α≥γD.α≤β,α≤γ
思路:該題若用極限思想則考慮兩個極端位置,在初始位置,易知α=π,α>β,α=γ,在B折平時易知α=β=0,α<γ,易得正確答案為B,此法為學生限時條件下解決選擇題的有效方法.
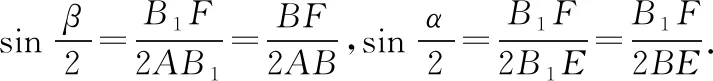
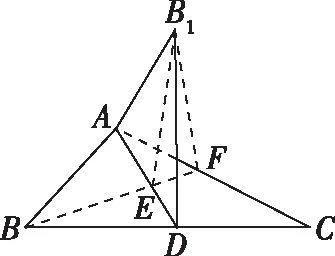
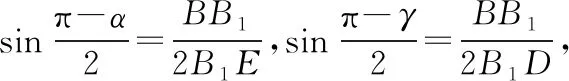
點評:立體幾何翻折問題常先考慮折之前圖形與折疊過程中的圖形的變量與不變量,也是極端法的緣由,其次該題通解法的紐帶是點B1投影一定落在AD的高線上.
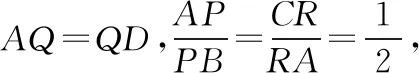
( )
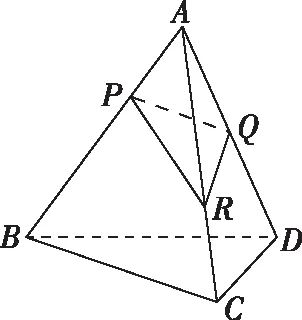
A.β>γ>αB.α>β>γ
C.α>γ>βD.β>α>γ
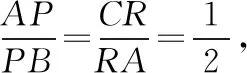
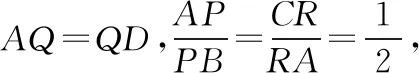
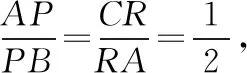
三、動態圓錐曲線視角
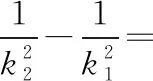
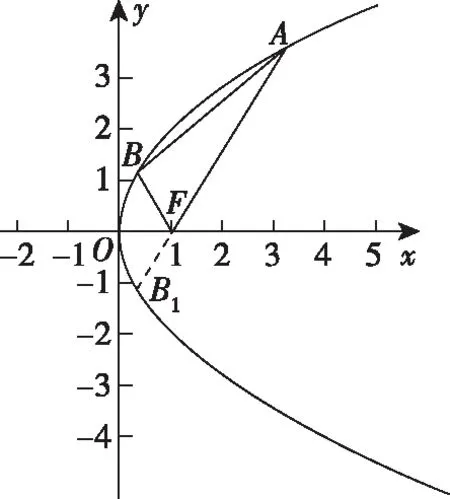
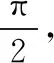
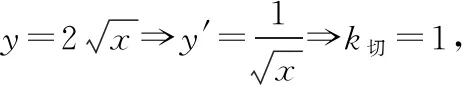
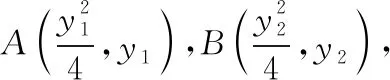
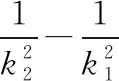
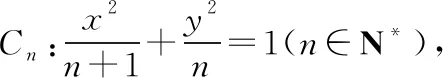
( )
A.遞增數列 B.遞減數列
C.先遞減后遞增數列 D.先遞增后遞減數列
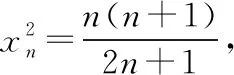
【教材習題】觀察不同的橢圓,我們發現,橢圓的扁平程度不一,那么,用什么量可以刻畫橢圓的扁平程度呢?
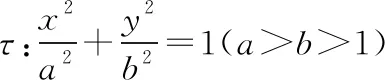
( )
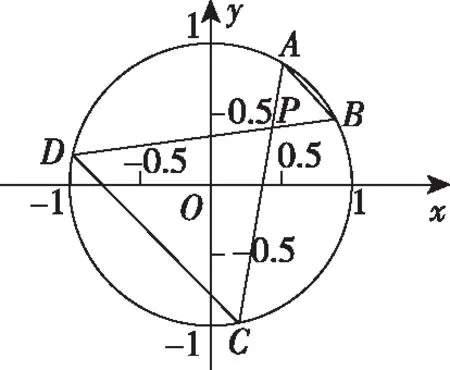
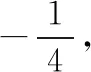
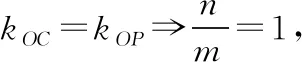
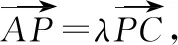
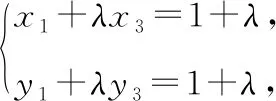
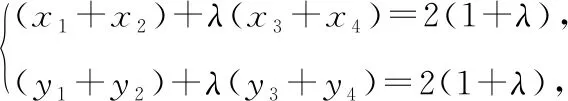
(x1+x2)+λ(x3+x4)=(y1+y2)+λ(y3+y4),
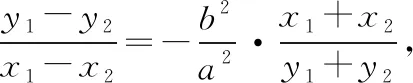
所以a2(y1+y2)=4b2(x1+x2),同理有a2(y3+y4)=4b2(x3+x4),