雙重非均勻系統反應性等效物理轉換方法

婁 磊，柴曉明，姚 棟，彭星杰，李滿倉，于穎銳，王連杰

(中國核動力研究設計院 核反應堆系統設計技術重點實驗室,成都610213)

顆粒型彌散燃料和彌散可燃毒物已在核反應堆工程中得到應用[1-2]。顆粒型彌散燃料能夠包容裂變產物，在高溫和深燃耗情況下可確保燃料的完整性，有效防止放射性物質擴散。顆粒型彌散可燃毒物能夠依靠毒物顆粒的自屏效應，實現堆芯反應性的長期平穩控制，通過控制顆粒尺寸，可提高使用可燃毒物的靈活性。但與常規燃料芯體相比，顆粒型彌散系統在常規柵格層面的非均勻性基礎上，增加了微觀層面彌散顆粒與基體的非均勻性，因此，具有雙重非均勻性。傳統中子學計算軟件僅能描述和處理柵格層面的非均勻性，不能處理雙重非均勻系統中顆粒的自屏效應。

為解決雙重非均勻性問題，反應堆物理學者們提出了眾多方法，其中主要有蒙特卡羅方法和確定論方法。蒙特卡羅方法主要采用顯式建模或弦長抽樣方法，如MCNP6[3]、Serpent[4]、MVP[5]及RMC[6]等；確定論方法主要是在不同層面以等效或修正的方法處理雙重非均勻效應，如韓國Kim等采用的體積均勻化(volumetric homogenization，VH)方法是最簡單的處理方法[7]，但忽略了彌散顆粒的空間自屏。Kim等還提出用反應性等效物理轉換(reactivity-equivalent physical transformation, RPT)方法處理彌散顆粒燃料的雙重非均勻系統[7]，但該方法在處理彌散可燃毒物顆粒的雙重非均勻性時效果不佳。隨后，Li等提出改進的RPT(improved RPT， IRPT)方法，用于處理同時含有彌散燃料和彌散可燃毒物的系統[8]。Shmakov等和She等分別提出了不同的等效均勻化方法[9-10]，這些方法在處理彌散燃料和彌散可燃毒物時精度較高，且方法簡單，但需要額外計算Dancoff因子，僅適用于蒙特卡羅程序或含有等價理論模塊的確定論程序。Sanchez等和Hebert等分別提出了基于特征線方法(method of characteristic， MOC)和碰撞概率方法(collision probability method， CPM)的雙重非均勻性輸運計算方法[11-14]，這些方法的理論嚴密，能夠處理彌散燃料和彌散可燃毒物，但需要對現有程序做出大量修改。哈爾濱工程大學Zhang等、Li等及Liang等分別將MOC方法用于特征線程序中，對方法進行了改進和驗證[15-18]。西安交通大學Yin等提出超細群方法，并結合MOC方法處理雙重非均勻性問題，適用于超細群程序[19]。此外，Okumura等采用的SRAC程序基于首次碰撞概率守恒理論修正顆粒的自屏截面，對彌散顆粒區域進行了均勻化處理，研究了彌散燃料的雙重非均勻問題[20]。

本文在對RPT方法和IRPT方法深入研究的基礎上，提出了環形反應性等效物理轉換(ring RPT，RRPT)方法和雜交反應性等效物理轉換(hybrid RPT，HRPT)方法，分別用于處理含有單顆粒類型的雙重非均勻系統和同時含有彌散燃料及彌散可燃毒物的雙顆粒類型的雙重非均勻系統，計算結果表明，RRPT方法和HRPT方法具有更高的計算精度和更廣的適用范圍。

1 方法介紹

1.1RPT方法和IRPT方法

針對一種顆粒類型的雙重非均勻系統，可采用RPT方法處理。圖1為柱狀和球狀幾何的RPT方法示意圖。首先，全部燃料球顆粒被壓縮在一個較小的燃料區內；其次，對壓縮后的雙重非均勻性燃料區，采用體積權重進行均勻化，并采用傳統的壓水堆組件-堆芯計算流程進行計算。在RPT方法中，通過保證系統的kinf與參考解相等，從而確定壓縮后燃料區的半徑。參考解通過高保真的確定論程序或蒙特卡羅程序計算得到。

對同時含有彌散燃料和彌散可燃毒物的雙重非均勻系統，可采用IRPT方法處理。圖2為IRPT方法示意圖。IRPT方法也稱為兩步RPT方法。首先，對不含彌散可燃毒物的系統采用RPT方法進行處理，得到第1步的RPT半徑R1；其次，加入彌散毒物，對壓縮后的區域用RPT方法再次處理，得到第2步的RPT半徑R2。

圖1 柱狀和球狀幾何的RPT方法示意圖Fig.1 Schematic diagram of the RPT method

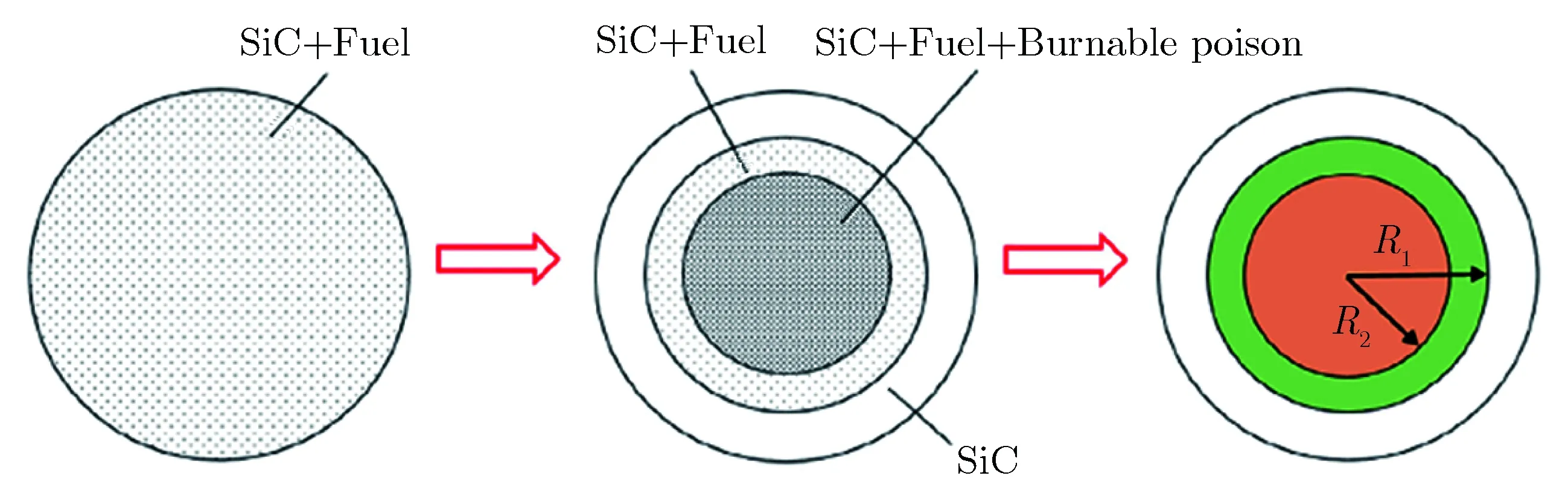
圖2 IRPT方法示意圖Fig.2 Schematic diagram of the IRPT method

1.2 RRPT方法與HRPT方法

本文提出用RRPT方法處理單顆粒類型的雙重非均勻系統。RRPT方法將彌散顆粒材料壓縮為環形區域，可以更好地模擬彌散顆粒的空間自屏效應。圖3為RRPT方法示意圖。RRPT方法的計算過程只有1步，即將全部的彌散顆粒材料壓縮為一個環形區域。對于柱狀幾何，環形區域為一個圓環柱；對于球形幾何，環形區域為一個圓環殼。在保持環形區域顆粒材料的總量與原雙重非均勻系統顆粒總量不變的前提下，圓環內徑變化，則圓環的厚度和外徑隨之變化。當系統壽期初的反應性與參考解相等時，系統的內徑即為RRPT方法的RPT半徑R。

針對同時含有燃料顆粒和毒物顆粒的雙顆粒類型的雙重非均勻系統，本文提出用HRPT方法進行處理。

圖4為HRPT方法示意圖。該方法是將RPT方法與RRPT方法結合，首先使用RPT方法處理除去彌散可燃毒物后的雙重非均勻系統，得到第1步的RPT半徑R1；然后加入彌散毒物，對壓縮后的區域采用RRPT方法處理，得到第2步的環形RPT半徑R2，in和R2，out。由外至內可獲得的4個環形區域，依次是基體、燃料-基體混合物、毒物、燃料-基體混合物。其中，2個燃料-基體混合物區域的材料成分完全相同。

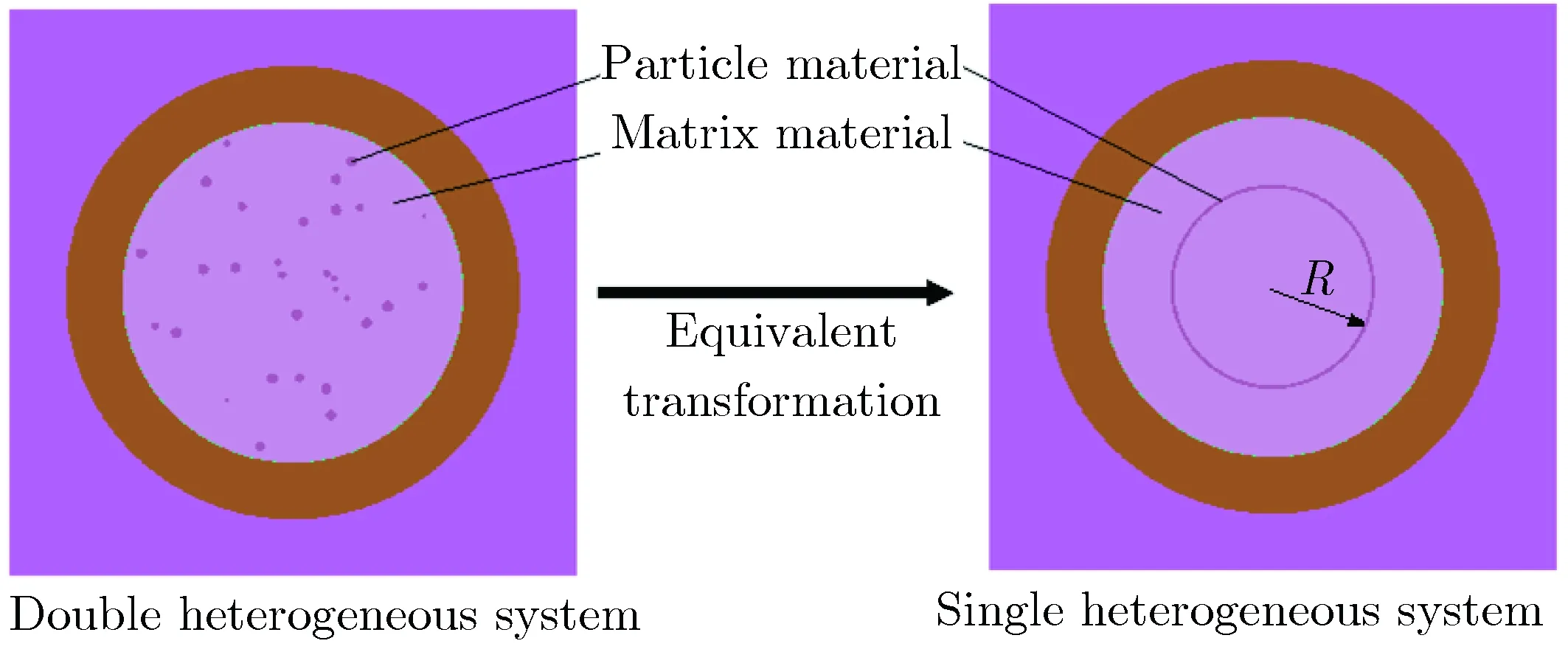
圖3 RRPT方法示意圖Fig.3 Schematic diagram of the RRPT method

圖4 HRPT方法示意圖Fig.4 Schematic diagram of the HRPT method

2 計算驗證

2.1 算例描述

2.1.1單顆粒類型算例描述

為驗證單燃料顆粒或單可燃毒物顆粒的雙重非均勻系統，本文構造圓柱形柵元，Zr基體中彌散燃料球的相關參數，如表1所列。

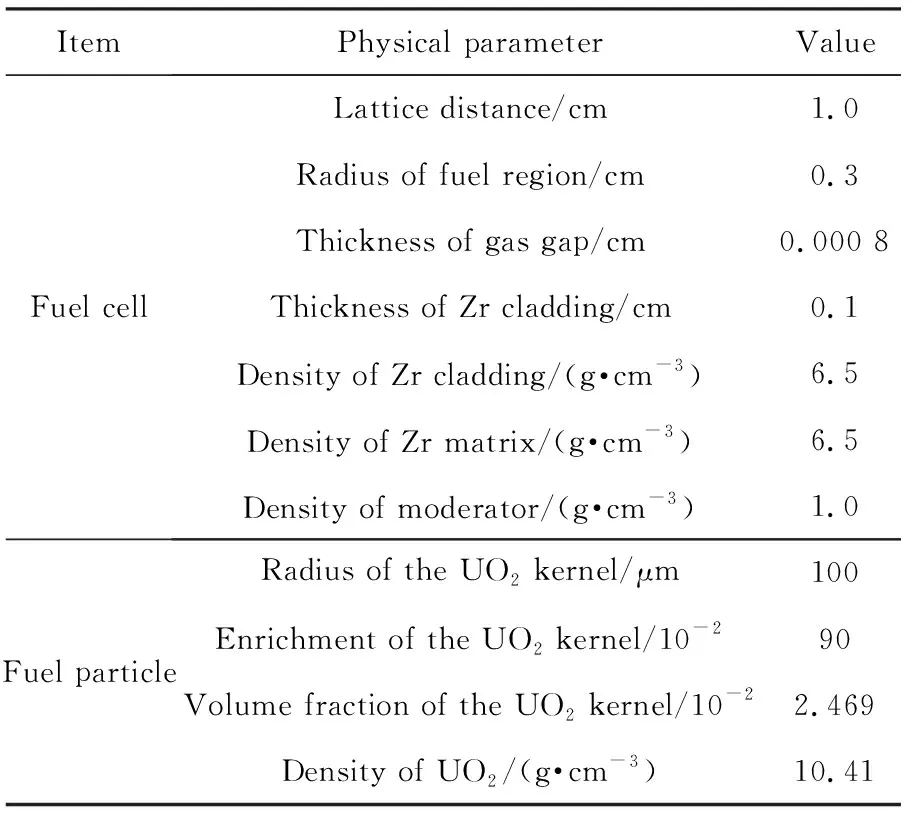
表1 單顆粒類型彌散燃料雙重非均勻系統的相關參數Tab.1Parameters of double-heterogeneous systems withsingle type of fuel particles

UO2芯體中彌散可燃毒物顆粒的相關參數，如表2所列。圖5為單顆粒類型雙重非均勻系統算例示意圖，柵元外邊界條件為全反射。

2.1.2 雙顆粒類型算例描述

為驗證雙顆粒類型的雙重非均勻系統，本文構造了圓柱形柵元， Zr基體中同時彌散燃料球和可燃毒物球。含彌散燃料和彌散可燃毒物的雙顆粒類型的雙重非均勻系統相關參數，如表3所列。

表2 單顆粒類型彌散可燃毒物雙重非均勻系統的相關參數Tab.2Parameters of double-heterogeneous systemswith single type of burnable poison particles

(a)Side view

(b)Top view圖5 單顆粒類型雙重非均勻系統算例示意圖Fig.5 Schematic diagram of double-heterogeneoussystem of single type of particles

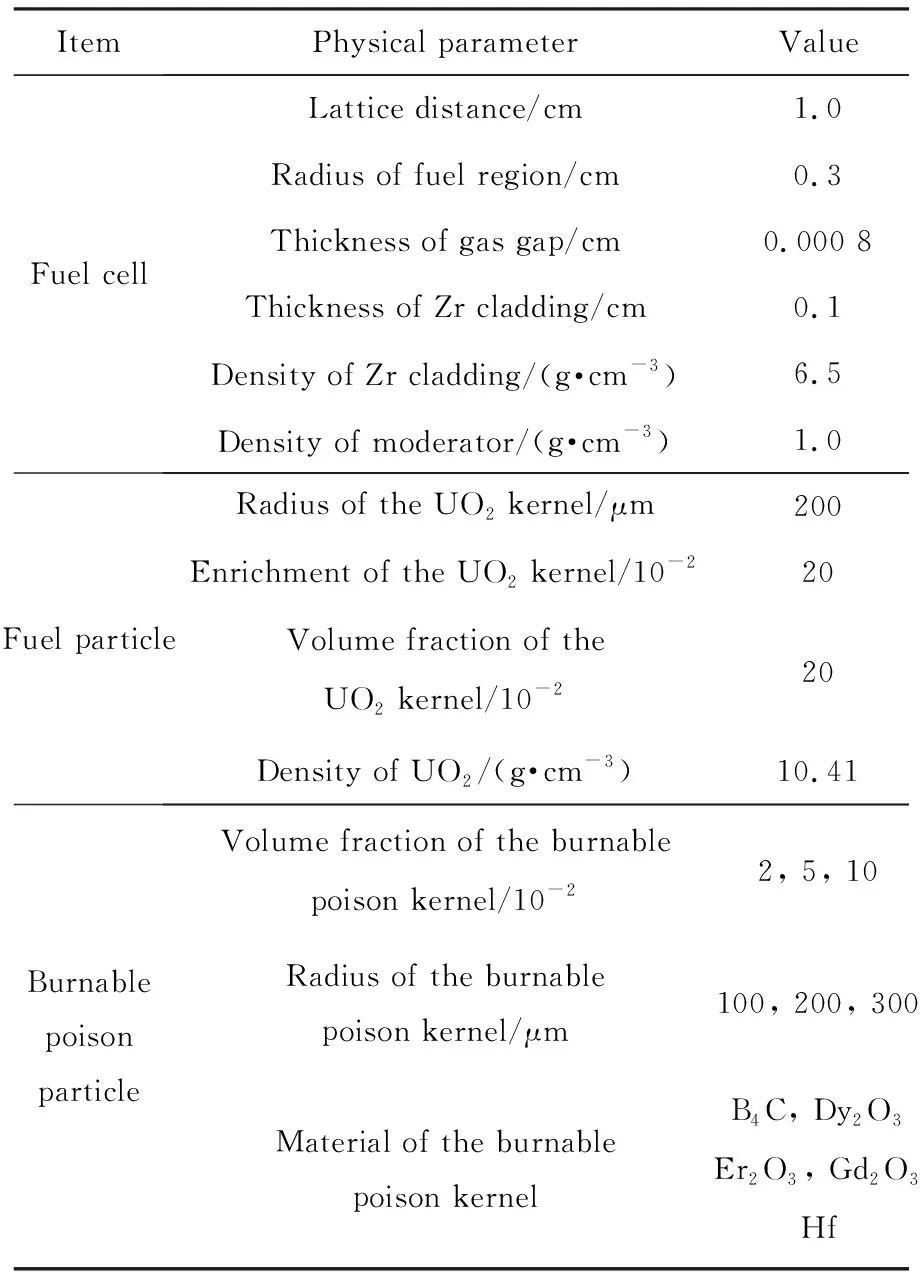
表3 含彌散燃料和彌散可燃毒物的雙重非均勻系統相關參數Tab.3 Parameters of double-heterogeneous systems with twotypes of fuel and burnable poison particles

圖6為雙顆粒類型的雙重非均勻系統示意圖，柵元外邊界條件為全反射。

(a)Side view

(b)Top view圖6雙顆粒類型的雙重非均勻系統示意圖Fig.6 Schematic diagram of double-heterogeneoussystem of two types of particles

2.2 計算結果

RMC是由清華大學開發的蒙特卡羅計算程序[6]，可對雙重非均勻系統的彌散顆粒進行顯式模擬，模擬結果可作為基準解驗證其他計算方法的準確性。本文使用的RRPT方法、HRPT方法、RPT方法及IRPT方法均是將雙重非均勻系統等效為無彌散顆粒的單重非均勻系統，然后再進行計算，不僅適用于確定論程序，而且適用于蒙特卡羅程序。為消除不同程序間的計算偏差，本文首先使用各種方法對雙重非均勻系統進行等效，然后采用RMC計算等效后的單重非均勻系統參數，將計算結果與RMC顆粒模型(grain model， GM)的計算結果進行比較，以評價各種方法的計算精度。

2.2.1單顆粒類型計算結果

采用RRPT方法、RPT方法、VH方法及GM分別計算了單顆粒類型雙重非均勻系統的kinf及反應性，并以GM計算的反應性為基準，計算了其他方法得到的反應性與GM計算的反應性之差δ，得到kinf及δ隨燃耗的變化關系，如圖7所示。

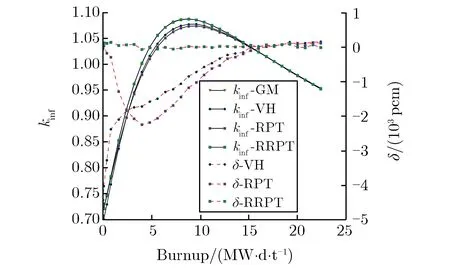
(a)B4C

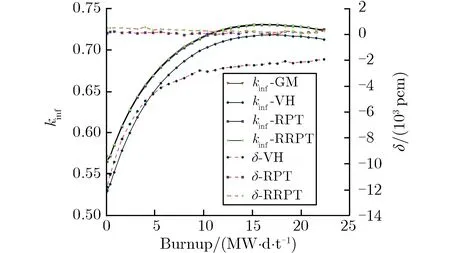
(b)Dy2O3

(c)Er2O3

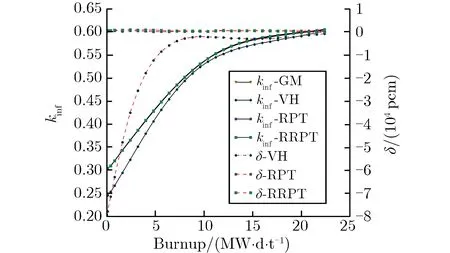
(d)Eu2O3

(e)Gd2O3

(f)UO2圖7單顆粒類型算例的計算結果Fig.7 Results of single type particle cases

由圖7可見，對于UO2燃料顆粒，當燃料富集度高達90%時，燃耗過程中，VH方法的δ約為500 pcm，而RRPT方法和RPT方法的δ均幾乎為0 pcm。對于B4C，Dy2O3，Er2O3，Eu2O3，Gd2O3等可燃毒物顆粒，壽期內VH方法的δ均較大。對于Dy2O3和Er2O3等吸收截面較小的毒物顆粒，壽期內RPT方法和RRPT方法的δ均小于500 pcm。對于B4C，Eu2O3，Gd2O3等吸收截面較大的可燃毒物顆粒，壽期內RPT方法的δ較大，而RRPT方法的δ均較小。

計算結果表明，對于單顆粒類型雙重非均勻系統中的彌散燃料顆粒，VH方法的δ尚可接受；對于單顆粒類型雙重非均勻系統中吸收截面較小的彌散可燃毒物顆粒，不能采用VH方法處理，可以采用RPT方法進行處理。而對于單顆粒類型雙重非均勻系統中吸收截面較大的彌散可燃毒物顆粒，VH方法和RPT方法均會產生較大的δ，必須采用RRPT方法進行處理。

2.2.2雙顆粒類型計算結果

對于雙顆粒類型的雙重非均勻系統，本文分別采用HRPT方法、IRPT方法及GM進行處理，計算了kinf和反應性，并以GM計算的反應性為基準，計算了其他方法得到的反應性與GM計算的反應性之差δ，得到kinf及δ隨燃耗的變化關系，如圖8所示。需要說明的是，由于VH方法與GM的反應性偏差太大，故本文未列出相應的計算結果。由于不同毒物顆粒的吸收截面不同，故本文采用多種毒物顆粒進行驗證，在毒物顆粒不同的體積分數下，分析對比了不同處理方法的優劣。

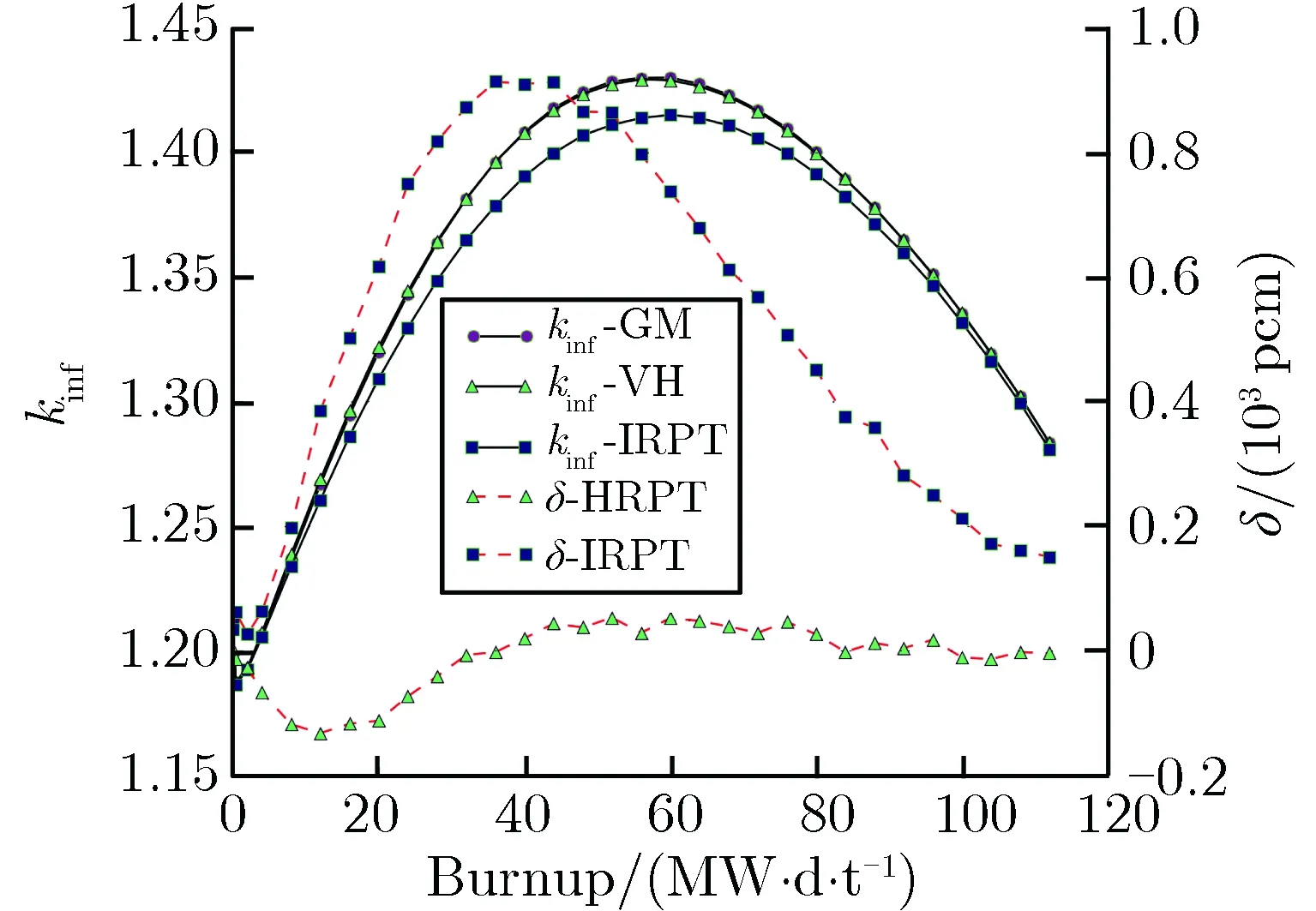
(a)B4C-2%-100 μm

(b)B4C-2%-200 μm

(c)B4C-5%-300 μm

(d)B4C-10%-200 μm

(e)Dy2O3-2%-100 μm

(f)Dy2O3-2%-200 μm

(g)Dy2O3-2%-300 μm

(h)Er2O3-2%-100 μm

(i)Er2O3-2%-200 μm

(j)Er2O3-2%-300 μm

(k)Gd2O3-2%-100 μm

(l)Gd2O3-2%-200 μm

(m)Gd2O3-2%-300 μm

(n)Hf-2%-100 μm

(o)Hf-2%-200 μm

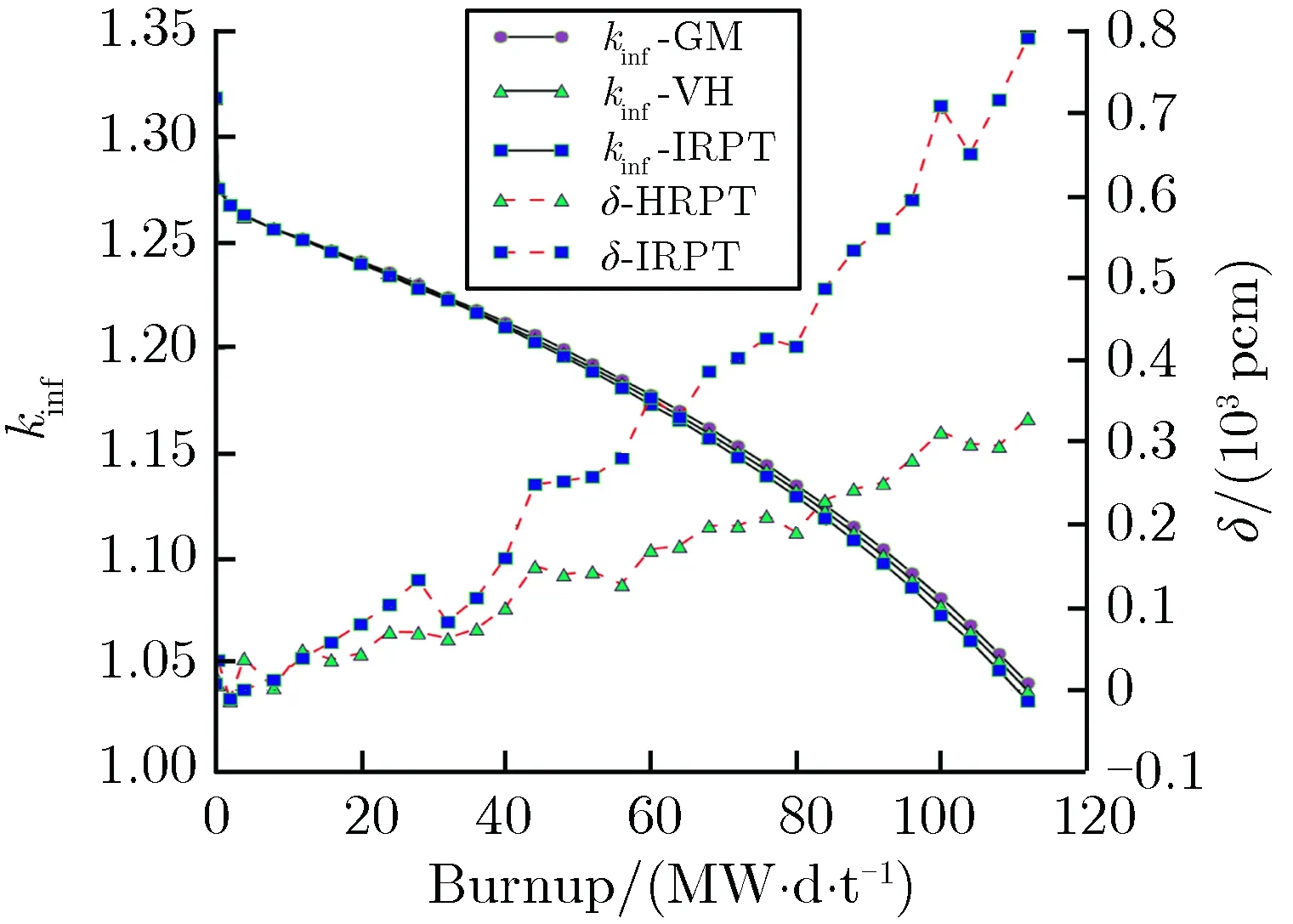
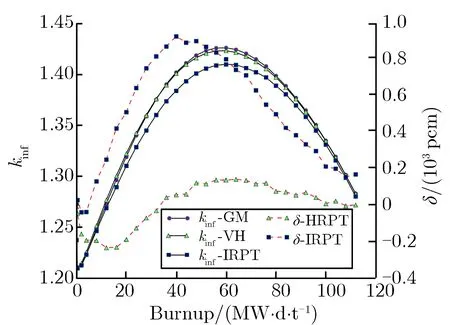
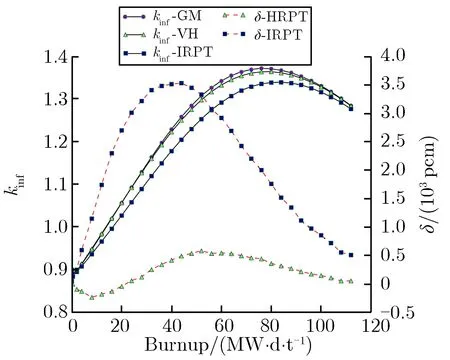
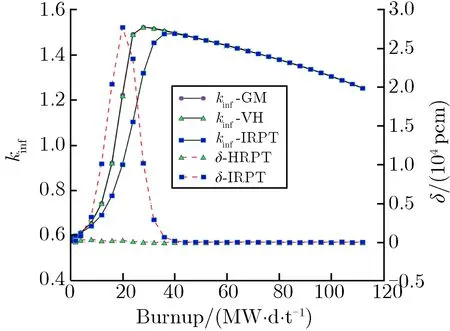
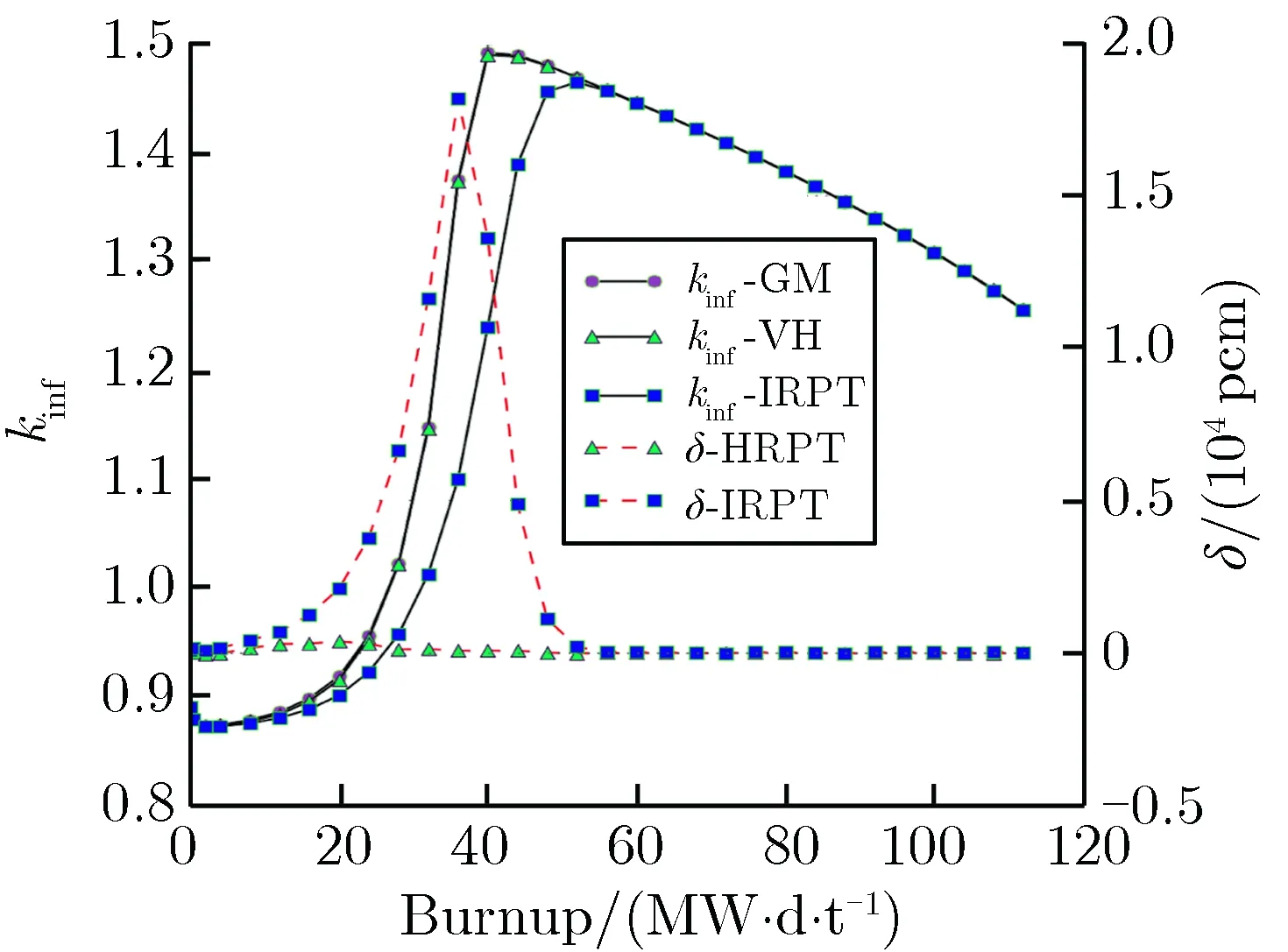
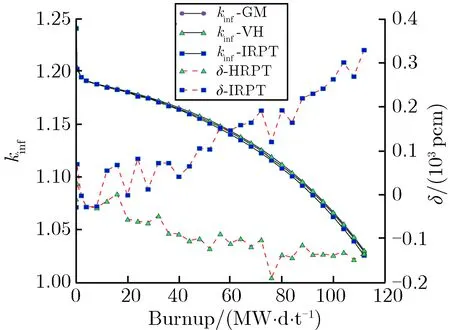
(p)Hf-2%-300 μm圖8雙顆粒類型算例計算結果Fig.8 Results of two types particle cases

由圖8結果可見，對于吸收截面較大的彌散毒物顆粒B4C，IRPT方法在燃耗過程中的反應性與GM的反應性存在較大偏差，在B4C顆粒體積分數高達10%、且顆粒尺寸為200 μm時，HRPT方法的δ可以保持在500 pcm以內。對于吸收截面相對較小的Dy2O3，Er2O3，Hf，當體積份額為2%，顆粒尺寸分別為100 μm和200 μm時，IRPT方法和HRPT方法壽期內的δ均能保持在500 pcm以內，HRPT方法的δ略小于IRPT方法，但當顆粒尺寸為300 μm時，IRPT方法壽期內的δ已超過500 pcm。對于吸收截面更大的Gd2O3彌散毒物顆粒，當體積分數為2%，顆粒尺寸分別為100，200，300 μm時，IRPT方法壽期內的δ均較大，而HRPT方法壽期內的δ均在500 pcm以內。對于顆粒尺寸為300 μm的算例，如圖8(j)和圖8(p)，HRPT方法的δ雖小于500 pcm，但仍然較大，這是由于顆粒尺寸較大，燃耗過程中顆粒半徑的變化相對比較明顯，HRPT方法在壽期初的等效方式可能在燃耗過程中不太適用。盡管如此，HRPT方法的δ仍在工程可接受范圍之內。

圖8計算結果表明，針對同時含有彌散燃料和彌散可燃毒物的雙顆粒類型的雙重非均勻系統，對于Dy2O3，Er2O3，Hf等吸收截面較小的顆粒可燃毒物，當體積分數在2%以內，顆粒尺寸在200 μm以內時，可以采用IRPT方法進行處理，而對于其他吸收截面較大的可燃毒物顆粒，建議采用HRPT方法進行處理。

3 結論

本文針對單顆粒類型的雙重非均勻系統和同時含有彌散燃料顆粒和彌散可燃毒物顆粒的雙顆粒類型的雙重非均勻系統，分別提出了RRPT方法和HRPT方法，并通過典型算例將本文方法與RPT方法和IRPT方法進行了對比分析。結果表明，RPT方法可以處理彌散燃料顆粒和吸收截面較小的彌散可燃毒物顆粒，對于吸收截面較大的可燃毒物顆粒，RRPT方法優于RPT方法。IRPT方法可以處理同時含有彌散燃料顆粒和彌散可燃毒物顆粒的雙顆粒類型的雙重非均勻系統，對于吸收截面相對較小且顆粒尺寸相對較小的系統，IRPT方法的計算精度較好，當彌散可燃毒物顆粒的吸收截面較大或體積份額較大時，HRPT方法的計算精度明顯高于IRPT方法。