基于核心素養(yǎng)視閾例談模型思想的建構(gòu)策略

天津市濱海新區(qū)塘沽福州道小學(xué) 宋春霞 ■天津師范大學(xué) 張璐迪

核心素養(yǎng)理念指出當(dāng)下教育應(yīng)以學(xué)生的關(guān)鍵能力和必備品格為培養(yǎng)核心，有利于學(xué)生綜合素養(yǎng)的整體提升。知識是素養(yǎng)形成的載體，離開課堂教學(xué)的支撐，學(xué)生的核心素養(yǎng)難以形成。模型思想揭示了數(shù)學(xué)內(nèi)在的本質(zhì)結(jié)構(gòu)，是數(shù)學(xué)最核心的部分。《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）》指出：“模型思想的建立是學(xué)生體會和理解數(shù)學(xué)與外部世界聯(lián)系的基本途徑。”模型思想是連接數(shù)學(xué)與生活實(shí)際的有效橋梁，有助于提高學(xué)生的應(yīng)用意識，對學(xué)生思維能力的培養(yǎng)至關(guān)重要，理應(yīng)成為核心素養(yǎng)視野下教師教學(xué)關(guān)注的焦點(diǎn)。那么我們到底該如何構(gòu)建模型思想呢？筆者以四年級上冊《烙餅問題》為例，談一談基于核心素養(yǎng)視閾模型思想的建構(gòu)策略。

一、在具體情境中引入模型

新課程標(biāo)準(zhǔn)提出：讓學(xué)生經(jīng)歷或體驗從日常生活中、從具體情境中抽象出數(shù)或數(shù)學(xué)符號的過程。教材選取了現(xiàn)實(shí)生活中烙餅問題為教學(xué)載體，將枯燥、單調(diào)的數(shù)學(xué)思考置于貼近生活實(shí)際的場景中，喚醒學(xué)生已有的生活經(jīng)驗，激發(fā)他們主動探究的欲望。“優(yōu)化策略”較抽象，對于第二學(xué)段起始年級的學(xué)生而言理解這類問題有一定難度。為排除困難，教材將“優(yōu)化策略”的學(xué)習(xí)任務(wù)與學(xué)生生活中常見的烙餅事件相融合。新課伊始，筆者將“媽媽正在烙餅”的主題圖作為切入點(diǎn)，學(xué)生觀察主題圖后搜集已知信息和所求問題，經(jīng)歷了從生活原型到數(shù)學(xué)模型的過程。

有效理解問題情境是實(shí)現(xiàn)數(shù)學(xué)模型建構(gòu)的首要環(huán)節(jié)。學(xué)生在了解烙餅規(guī)則的基礎(chǔ)上，要重點(diǎn)理解“每次最多只能烙2 張”和“兩面都要烙”的含義，并與小伙伴分享。隨后師生以“烙餅活動”為主題，以問題為驅(qū)動，從烙1 張餅開始，緊緊圍繞“怎樣烙餅最省時”展開探究，餅的數(shù)量由少到多。學(xué)生借助圖形直觀、操作驗證、觀察對比、思考擇優(yōu)等方法，逐漸發(fā)現(xiàn)烙不同張數(shù)大餅時“怎樣烙才最省時間”的實(shí)踐策略。

在生活中的具體情境中引入模型，學(xué)生思維會快速聚焦到具體的問題情境和烙餅規(guī)則上，易于從中抽象出數(shù)學(xué)問題。將“優(yōu)化策略”置于此問題情境中，能夠激發(fā)學(xué)生主動探究欲望和潛能，使其在已有的知識經(jīng)驗和活動經(jīng)驗基礎(chǔ)上，生發(fā)更深層次的數(shù)學(xué)思考，為后續(xù)感知“優(yōu)化策略”的數(shù)學(xué)模型、積累新的探究活動經(jīng)驗提供素材。

二、在動手操作中感知模型

四年級學(xué)生的抽象邏輯思維仍然與感性經(jīng)驗相聯(lián)系，建立“優(yōu)化問題”的數(shù)學(xué)模型必須要經(jīng)歷烙餅問題中對數(shù)量關(guān)系和數(shù)學(xué)規(guī)律的抽象過程，并用簡潔、規(guī)范的數(shù)學(xué)語言概括描述出相應(yīng)規(guī)律，該過程對第二學(xué)段起始年級的學(xué)生來說有一定難度。瑞士心理學(xué)家皮亞杰提出：“思維起源于動作。”所以動手操作是學(xué)生獲取新知的有效途徑。課堂教學(xué)中，筆者設(shè)計了以組為單位的實(shí)踐操作性活動，抽象的烙餅過程在動手操作中更為直觀化。在探究2張餅的烙法時，學(xué)生以“手”替代餅，根據(jù)烙餅規(guī)則演示烙的過程。在探究3張餅的烙法時，學(xué)生利用圓形學(xué)具（直觀模型）代替餅，根據(jù)烙餅規(guī)則探尋最省時的烙法。學(xué)生邊操作邊借助數(shù)學(xué)語言和肢體語言與同伴交流演示自己的想法。此環(huán)節(jié)分為3 個層次。層次一，猜想。學(xué)生在探究怎樣烙2張餅最省時間的實(shí)踐基礎(chǔ)上，根據(jù)自己已有的認(rèn)知經(jīng)驗和活動經(jīng)驗大膽猜想“烙3 張餅最少需要多少分鐘”，并與同伴分享猜想的依據(jù)。層次二，動手實(shí)踐、驗證猜想。全班分組活動，先討論怎樣烙3張餅最省時，然后從教師提供的學(xué)具中自選餅和鍋，組內(nèi)實(shí)踐操作，經(jīng)歷該探究過程，有助于在感知數(shù)學(xué)模型的過程中積累有效的數(shù)學(xué)思想方法和活動經(jīng)驗。層次三，展示分享。學(xué)生以組為單位向全班演示烙餅的操作過程，并匯報為什么這樣烙最省時，通過師生、生生多元互動共同修正認(rèn)知。在匯報交流的過程中，學(xué)生既了解到問題解決的多種策略，又體會到尋求最合理、最省時烙餅方案的“優(yōu)化思想”。在解決問題的過程中，學(xué)生手、腦、口并用，在觀察和操作中了解“優(yōu)化問題”的數(shù)學(xué)模型，并在認(rèn)識、理解模型中，獲得了必要的經(jīng)驗和感性認(rèn)識。

三、在合作探究中建立模型

新課程標(biāo)準(zhǔn)要求：數(shù)學(xué)學(xué)習(xí)的過程是學(xué)生自主發(fā)現(xiàn)、再創(chuàng)造的過程。由于學(xué)生年齡小、探究能力弱，展開建模活動時需要教師的有效指導(dǎo)。教師為學(xué)生準(zhǔn)備的“烙餅圖”是最貼近問題原型的直觀化表征模型，用大橢圓表示鍋、三個小圓分別表示餅，用兩種顏色區(qū)分餅的正面和反面，便于學(xué)生直觀呈現(xiàn)“交替烙”的詳細(xì)過程。

學(xué)生小組記錄單的設(shè)計重視操作圖與表格的直觀對應(yīng)，不僅能清楚記錄餅數(shù)及正反面，還能直接反映所需時間和次數(shù)，幫助學(xué)生掌握建模的方法。在分享、交流“烙3 張餅的最優(yōu)策略”時，借助圖形，教師能更直觀有效地對學(xué)生建模進(jìn)行指導(dǎo)和幫扶。

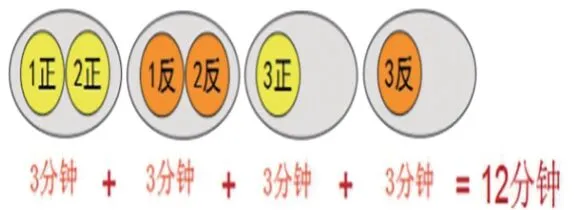
方案一：

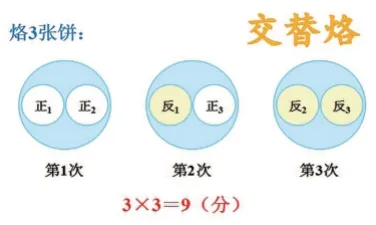
方案二：

在方案對比中，學(xué)生發(fā)現(xiàn)“用第一種方法烙第3張餅時，本來一次可以烙2張餅的鍋現(xiàn)在只烙了1張，浪費(fèi)了空間和時間。”教師順勢引導(dǎo)學(xué)生直擊問題關(guān)鍵——“保證鍋里同時烙2張餅”“沒有空余”才是最優(yōu)的烙餅策略，初步建立“烙3張餅”的數(shù)學(xué)模型。

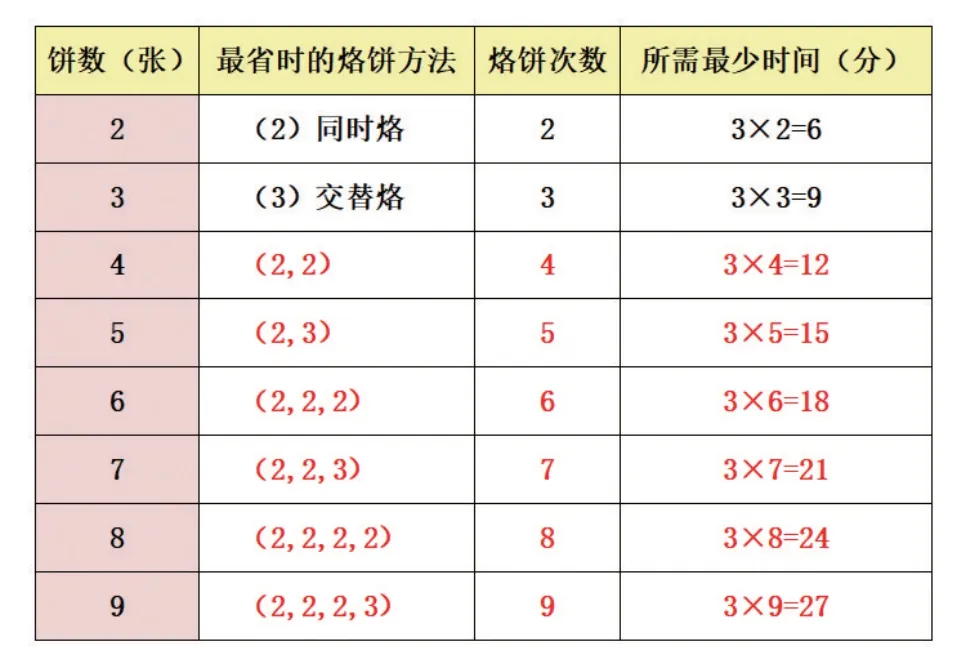
學(xué)生在探究烙3 張餅最優(yōu)烙法的過程，已有的知識和生活經(jīng)驗已經(jīng)被激活。隨后教師因勢利導(dǎo)，組織學(xué)生分組討論：借助烙2張餅和3張餅最優(yōu)烙法的經(jīng)驗，請猜一猜“如果要烙4 張……9 張餅怎樣烙最省時？動手烙一烙驗證你們的猜想，操作、對比后說說有什么發(fā)現(xiàn)？”學(xué)生在小組里先借助經(jīng)驗猜想怎樣烙最省時，在動手操作中驗證怎樣烙最省時，觀察后推理構(gòu)建模型，最后抽象概括表達(dá)出模型，即最省時的烙法：烙2、4、6等雙數(shù)張餅時，2張2張同時烙最省時；烙5、7、9等單數(shù)張餅時，先2張2張同時烙，最后3張交替烙就可以實(shí)現(xiàn)最優(yōu)解。借助圖將外化的動手操作濃縮為內(nèi)隱的深度思考，在動手操作中提升學(xué)生思維能力。此環(huán)節(jié)進(jìn)一步完善“烙餅問題”的最優(yōu)化方案，學(xué)生距離真正建立“烙餅問題”的模型只差一步。教師適當(dāng)引導(dǎo)學(xué)生觀察、分析表格：

?

通過分析表格，學(xué)生的思維從“餅的張數(shù)”過渡到“烙餅次數(shù)”，使感性經(jīng)驗轉(zhuǎn)化為理性經(jīng)驗，發(fā)現(xiàn)并總結(jié)出“烙餅問題”背后蘊(yùn)含的規(guī)律。即單面所需時間×餅數(shù)=最短用時（餅數(shù)≥2），從而成功構(gòu)建“烙餅問題”的數(shù)學(xué)模型。

建構(gòu)數(shù)學(xué)模型不僅僅是要得到最終的規(guī)律、結(jié)論，更需要經(jīng)歷模型構(gòu)建的過程，還要收獲數(shù)學(xué)模型構(gòu)建的方法、經(jīng)驗。學(xué)生從發(fā)現(xiàn)問題—提出問題—解決問題—?dú)w納數(shù)學(xué)規(guī)律—建構(gòu)數(shù)學(xué)模型五個環(huán)節(jié)中建立了數(shù)學(xué)模型。

四、在應(yīng)用中感受模型價值

建立模型就是為了運(yùn)用模型解決問題。在鞏固應(yīng)用環(huán)節(jié)中，筆者不僅設(shè)計了和烙餅問題類似的煎魚、打游戲的情境，還安排了教材的練習(xí)題。學(xué)生把構(gòu)建好的烙餅問題模型應(yīng)用到現(xiàn)實(shí)生活的問題解決中，深刻理解了“保證沒有空閑就是節(jié)省時間的最優(yōu)化策略”。學(xué)生在應(yīng)用模型解決生活中實(shí)際問題的過程中，逐步領(lǐng)悟到數(shù)學(xué)模型廣泛的應(yīng)用價值。這樣有利于激發(fā)學(xué)生進(jìn)一步研究數(shù)學(xué)建模的興趣和自信心，提高他們從具體問題中抽象出數(shù)學(xué)模型的能力，逐步形成自主建構(gòu)數(shù)學(xué)模型、靈活應(yīng)用數(shù)學(xué)模型探索和運(yùn)用模型解決問題的能力，借助數(shù)學(xué)模型思想助推學(xué)生數(shù)學(xué)思維能力的發(fā)展。

在日常教學(xué)中，我們要結(jié)合教學(xué)內(nèi)容突出數(shù)學(xué)與現(xiàn)實(shí)生活的聯(lián)系，讓學(xué)生感受到數(shù)學(xué)的應(yīng)用價值，在抽象、感知、理解、建立、應(yīng)用模型的過程中助推核心素養(yǎng)的形成。當(dāng)然，數(shù)學(xué)建模能力的形成和發(fā)展是一個長期的、循序漸進(jìn)的過程，教師在教學(xué)時要結(jié)合教學(xué)內(nèi)容有意識地為學(xué)生創(chuàng)造機(jī)會、搭建平臺，使核心素養(yǎng)的培養(yǎng)在學(xué)習(xí)過程中落地生根。