基于幾何光學近似迭代的多重散射波面分析
彭梓齊,楊江河
(湖南文理學院數理學院,中國 常德 415000)
光學遙感作為成熟的測量技術在工業、醫療、環保等領域得到了廣泛應用[1-7]。在光學遙感應用中,光在媒質中的傳播效率是影響光學測量結果與精度的一項重要參數。在散射粒子大量存在的高散射媒質(生物組織、大氣云層等)中,可視光以及紅外波段光會發生強烈的散射現象[8-12]。多重散射不僅使光波能量發散,導致傳播效率低下,同時使散射光偏光面發生變化,降低光學相干性,導致入射光原有的光學特性發生變化。如果能在高散射媒質中建立一種高效、穩定的傳播方法,將有利于提高光學遙感的測量范圍與精度。
環形波面的調制光在空氣中長距離傳播時,通過自身干涉效果可以形成一類強度分布為近似貝塞爾函數的波面。具有類波面的光通常被稱為非衍射光。理想的非衍射光波面中心集中大部分能量,波面強度分布不隨傳播距離的變化而變化,整個波面有抑制衍射的效果[13-17]。相比高斯分布的光源,在遠距離傳播的情況下環狀光在中心部位有著極高的傳播效率。
在前期的研究中[18-20],我們研究了在散射媒質中環狀光的傳播特性。通過實驗發現:收緊光學接收機視野角(3 mrad)的前提下,在特定濃度與深度的高散射媒質中,環狀光經過4~5次的多重散射之后,最終在出射面中心部形成中心波峰強度相對較高的干涉光,且中心主瓣周圍存在強度較弱的旁瓣。針對這一現象,還需要進一步的理論分析與數值解析。
數值解析不僅可以幫助驗證前期實驗結果的真偽,還為后期實驗的可行性提供分析與參考,是一項十分重要的內容。米氏散射理論是眾多散射理論中最為常用的理論之一,它以球體為散射解析對象,通過把電磁波的邊界條件代入球體模型,然后對電磁波傳播過程進行嚴密的求解從而得到球體后方的散射強度分布。這樣求得的單個球體散射模型被稱之為單散射。在針對多個散射球體同時存在且個數較少的情況下可以利用巴比涅原理對單散射模型進行疊加來實現分析多個球體的散射。另外,求解格林函數并進行疊加也是常見解析方法之一[21-23]。
前期研究的結果采用的散射媒質濃度較高,媒質中散射粒子極多,且粒子間距極小,這樣導致了粒子間發生多重散射,且粒子產生的散射光之間可能存在干涉效果,在這種情況下,采用米氏散射模型的疊加算法不能體現多重散射以及微小距離間散射光相互干涉的效果。在前期研究的實驗條件中,我們引入了收緊接收機視野角測量前方散射光的測量方法,在解析中同樣需要針對前方散射光的分析方法。根據以上條件,本文提出了一種基于簡化幾何光學近似的迭代解析方法,分析了環狀光多重散射現象中的前方散射光強度。在本文中,筆者首先敘述了簡化幾何光學近似的原理,運用該原理對單散射模型進行計算并與米氏散射理論結果比較,驗證了簡化幾何光學近似法的計算精度。在此基礎上,利用蒙特卡洛模擬與迭代方法,提出了一種由單散射過程迭代來實現多重散射的效果計算方法,對環狀光在散射媒質中的傳播進行了分析,并與實驗結果進行比對,評價了該分析方法的可靠性。
1 解析算法
前期研究采用了一般市場販賣的低脂肪加工純牛奶的稀釋液作為的高散射媒質的模型。加工純牛奶中脂肪球粒子大小相對均一,粒子濃度調節相對準確,適合作為散射媒質模型。采用的加工純牛奶中所含散射粒子主要為脂肪球的脂類與酪蛋白的蛋白質,平均粒子直徑分別為1.1 μm與0.1 μm。與脂肪球相比,酪蛋白粒子直徑只有脂肪球的1/10左右,散射截面大小只有脂肪球的1/100左右。酪蛋白粒子散射強度相比脂肪球粒子散射強度十分微小。實驗中采用了波長為660 nm的半導體激光作為光源,相對于波長為660 nm的光源,脂肪球粒子發生米氏散射,其異向性參數g的大小為0.936,散射光幾乎都集中在入射光軸方向。另一方面,酪蛋白粒子直徑遠小于光源波長,散射類型為瑞利散射,散射光在每個方向上的分布幾乎是均等的。根據這兩個條件,在收緊接收器視野角,觀測前方散射光的實驗前提條件下,解析中可以忽略酪蛋白產生前方散射光。本研究的解析算法中只考慮了脂肪球的散射影響。
1.1 粒子單散射模型
在粒子直徑大于光源波長的情況下,通常采用米氏散射理論[24]來分析球形粒子的單散射模型。米氏散射的散射強度受光源的波長影響小,而主要受散射角的影響。隨著粒子直徑的增大,米氏散射中的前方散射光部分也會逐漸增強。研究表明,散射粒子直徑相對較大的條件下,運用幾何光學近似法分析的單散射模型與米氏散射的分析結果基本一致[25,26]。此外,幾何光學近似采用菲涅爾解析可以準確計算出近場空間的散射光。基于以上理由,本文采用了幾何光學近似作為解析工具。
一般的幾何光學近似手法會考慮在散射球體上所發生的反射、折射、衍射過程,綜合分析散射強度[24]。由于前期研究實驗中測量的是前方散射光,本文采用的幾何光學近似也只考慮透射與衍射,而忽略了在前方散射上效果微弱的反射。光在穿過球體界面時,發生較大偏轉的折射光幾乎不能被小角度接收機接收,本次解析中為了簡化計算,我們同時忽略了光線在散射球體內部的折射偏轉,當光線穿過散射球體時,以直線光程來考慮。簡化后的幾何光學近似的模型如圖1所示。在多重散射光的干涉效果定量分析上,一般需要考慮到由多重散射所引起的偏光面變化,而前期研究中測量的前方散射光其偏光面基本不發生變化[20],所以在本解析方法中忽略了偏光面變化,直接采用了菲涅爾衍射公式來計算單散射的散射強度,散射光振幅大小可用下式來計算:
(1)
式中,u,u0分別為入射面與觀察面上入射光與散射光的振幅;(x0,y0)和(x,y)分別為入射面與觀察面上的位置坐標;k為波數;l為(x0,y0)到(x,y)上的距離,dσ為積分微小光源的寬度。對于任意觀察點,參照圖1,其光程l可用下式表示:
目前她已成為采油廠唯一的女油藏專家。工作十余年來,先后有150余項科研成果獲廠級以上獎勵,參與“孤島中一區Ng3聚驅后井網調整非均相復合驅”等9項中石化、油田分公司重大先導試驗項目,創直接經濟效益3億余元。
l=l1·n1+l2·(n2-n1),
(2)
式中,l1為幾何光程;l2為光線穿過散射球體內部時球體內部的光程差;n1,n2分別為媒質折射率與散射球體折射率。
在光程l的計算中,由于媒質內部的散射球體的分布是隨機的,需要確認二次波光線傳播方向與散射球體位置的相互關系。一般的方法是用隨機數確定粒子位置,然后從粒子位置與光線方向之間的關系來計算光程長度[27,28]。為了縮短計算時間,本研究采用新的算法來計算光程,平面的計算原理圖如圖2所示。
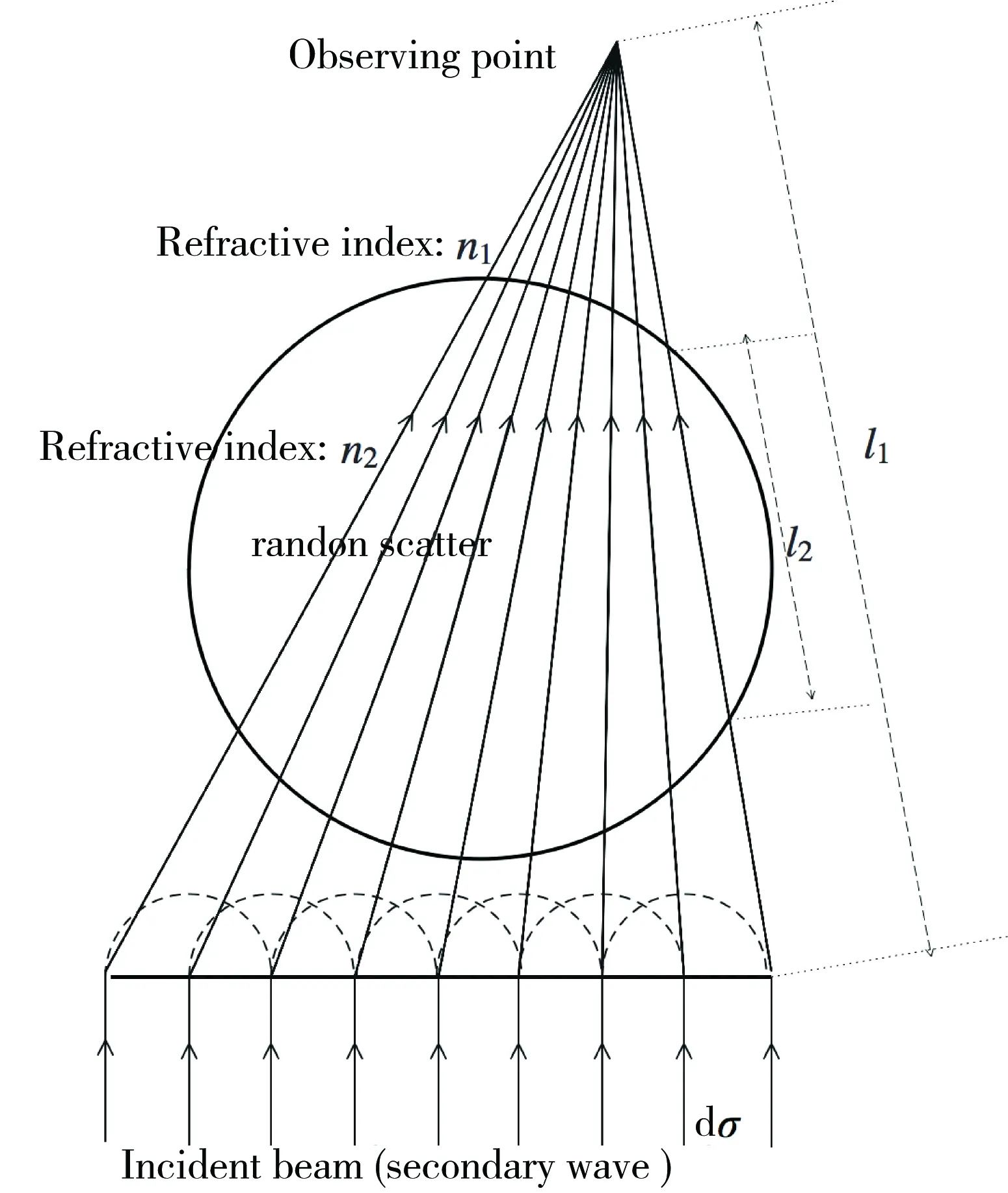
圖1 幾何光學近似Fig. 1 Geometric optics approximation
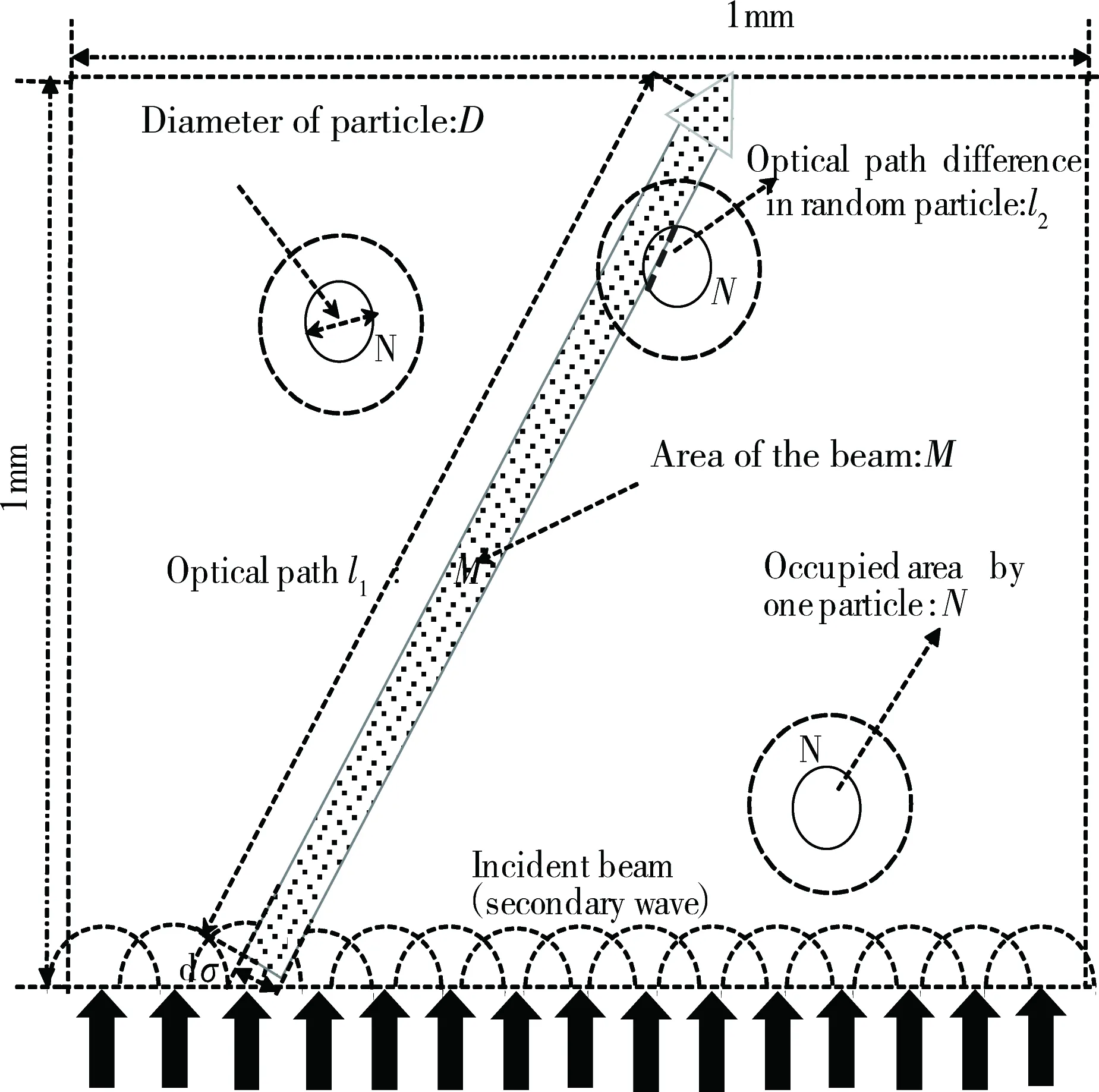
圖2 散射媒質中的光程計算圖示Fig. 2 Optical path calculation when light transmits in random media
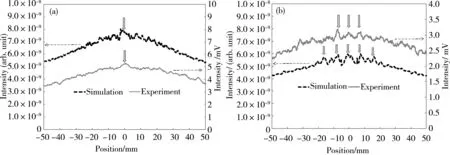
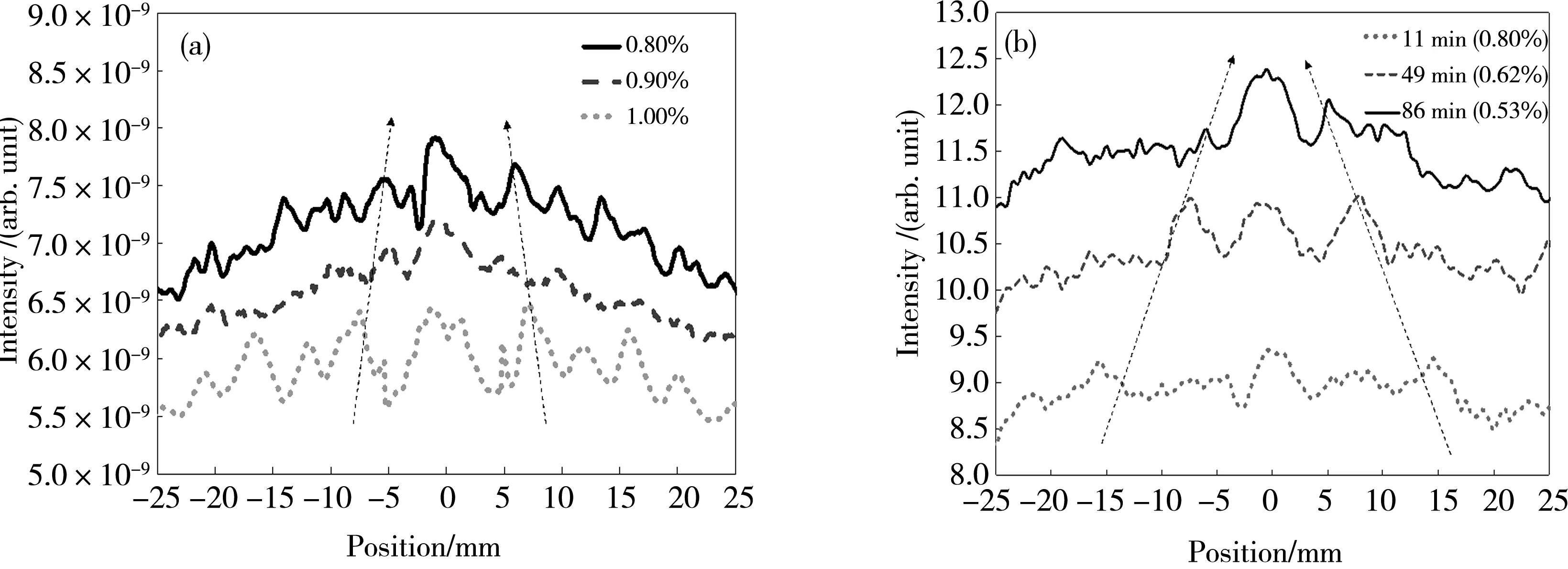
在1 mm長度的立方體空間內,式(1)中寬度為dσ的微小光源(對應圖1中的一條光線)在穿過該空間時,在平面上投影面積為M=l1* dσ。根據散射媒質的濃度以及圖2平面模型的物理厚度可以算出在1 mm×1 mm的平面內存在n’個散射球體。假設這些散射球體在平面上的投影不重疊且均勻分布,那么每個粒子在1 mm×1 mm的平面上所占有的面積為N= 1/n’ (mm2),每個散射球體在自己占據的面積內隨機運動。在這種情況下,把微小光源的光線與散射球體發生碰撞沖突的概率簡單的定義為S=M/N。通過產生0~1區間的隨機數R,在R>S的情況下光線不穿過散射球體,散射球體內部光程長l2為0;當R 前期研究中所用散射媒質為脂肪濃度1.8%的加工牛奶的稀釋液。稀釋濃度以0.1%為單位,最高濃度為1.0%(本文中所述“牛奶濃度”均指稀釋濃度,牛奶濃度1.0%指將加工牛奶稀釋100倍后的溶液)。媒質容器為長度20 cm的立方體玻璃水槽。實驗結果表明,在牛奶濃度為0.8%~1.0%的濃度范圍內,可以明顯觀測到中心干涉光效果[18-20]。根據濃度以及脂肪球的其他參數,使用下式可以求出光在此散射媒質中的平均自由程。 (3) 式中,a為脂肪球半徑;n為單位體積中的散射球體個數,Q為散射截面參數的Q值,g為異向性參數。 圖3 多重散射的分析模型(上方視角) Fig. 3 Analysis model for multiple scattering (view from above) 假設所有脂肪球在入射光方向上的投影沒有重疊,參考脂肪球的直徑大小、折射率以及生成中心干涉光時的牛奶濃度,可以計算出產生中心干涉光時光在散射媒質中的平均自由程為4~5 cm。實驗中采用的媒質容器長度為20 cm,可以計算出從環狀光入射散射媒質到射出散射媒質的過程中會發生4~5次散射,所以計算觀察面的波面時應考慮多重散射的效果。 為了將1.1節中所述簡化幾何光學近似的單散射模型擴展利用到多重散射模型中,我們將整個散射媒質在空間上分割成若干層,同時將每層分割為若干更小的單位空間。在每個單位空間中存在的散射球體數極少的情況下,可使用簡化幾何光學近似作為單散射模型處理。具體的媒質分割處理的平面圖如圖3所示。 為了檢驗1.1節中所提出的簡化幾何光學近似在單散射計算上的準確性,我們計算了空氣中水球體的散射光強分布,同時與米氏散射理論的計算結果進行了比較。計算中光源波長為630 nm;散射球體相對折射率為1.33;散射球體直徑分別為4,10和15 μm。 計算結果如圖4所示,橫軸為散射角度,縱軸為散射強度。由于幾何光學近似的計算手法中存在米氏散射計算中未考慮的直射光,幾何光學近似的計算結果在0°到1°的區間包含了極強的直射光強度,因而去掉了0 °到1 °附近的計算結果便于比較。從比較結果來看,在1°到15°附近的范圍里,散射強度的峰值以及該峰值所出現的散射角基本一致。在評價光軸附近的前方散射光的計算中是有效的。由于直射光的原因,兩者在0°到1°區間上有明顯的數值區別,在實驗中接收機所測量前方散射光中也包含了直射光的成分,實際的多重散射解析計算中,與實驗一樣直射光成分并未被去除,而是包含在計算中并在迭代計算中體現。 圖4 單散射波形計算結果 (a) 幾何光學近似. (b) 米氏理論Fig. 4 Single scattering waveform calculated by (a)Geometric optics approximation. (b) Mie theory 運用1.2節中所示的分割迭代計算的解析方法,計算散射媒質中光的透射率以及環狀光傳播的散射波面。計算中光源波長為660 nm,脂肪球平均直徑設為1.1 μm,水與脂肪球的折射率分別為1.33與1.45。 圖5 高斯光在散射媒質中的透射率 Fig. 5 Transmittance of Gaussian beam in random media 在光的透射率計算中,入射光為寬度6 mm的高斯光,通過在200 mm長的牛奶稀釋液中的傳播后,計算等寬部位入射前后的光強,將其比值作為透射率。計算所得透射率與實驗所得透射率如圖5所示。可以看出隨濃度變化的透射率在計算結果與實驗結果上是一致的,驗證了2.1節中所述直射光部分的正確性。散射媒質在0.1%~0.4%的范圍內,主要受單散射支配,透射率隨著濃度的升高而急劇下降。通過朗伯-比爾定律可知,媒質的散射系數σ可以由透射率的對數對濃度求微分而得到[29]。在濃度0.1%~0.4%范圍內,可依據圖5中透射率曲線的斜率求得散射系數σ1為158 cm-1,結果與通過米氏散射理論所計算的散射系數一致。在散射媒質濃度為0.5 %以上的區域,多重散射的效果逐漸增大,隨著濃度的增加,透射率的衰減率逐漸減小。當散射媒質濃度超過0.8%時,多重散射逐漸占據主導地位,通過圖5的透射率曲線斜率可以求得此時的散射系數為23 cm-1。把前方散射光作為透射光的一部分情況下,考慮到異向性參數g為0.936,在濃度為0.8 %的情況下,根據米氏散射理論所計算出的散射系數為23.3 cm-1。這與前述的透射率斜率計算結果也是一致的。其中異向性參數g的計算式如下式所示。 (4) 式中,θ為散射角;p(θ)為散射角為θ時的概率函數。 運用相同的計算方法,我們計算了與實驗參數相同的環狀光散射光波面,散射媒質長度為200 mm。環狀光參數設定為直徑40 mm,環厚3 mm。圖6(a)和(b)分別為牛奶濃度0.8%和1.0%時散射光波面的解析結果與實驗結果。牛奶濃度0.8%時,計算結果在波面中心出現了干涉波峰,其寬度與實驗結果相同。牛奶濃度1.0%時,計算結果在波面中心、左右兩側處出現了多個波峰,而實驗結果在波面中心、左右8 mm處出現了3個波峰。從比較的結果來看,本文采用的基于簡化幾何光學近似的迭代方法在多重散射的計算中是一種有效的模型。 我們也計算了牛奶濃度0.9 %時環狀光入射散射媒質所產生的散射波面。圖7(a)為牛奶濃度0.8%~1.0%時散射波面變化的計算結果,隨著散射媒質濃度的降低,散射光波面光強逐漸增強,散射波面中心干涉波峰強度也逐漸增強,而周圍的旁瓣有向中心靠攏的趨勢。另一方面,在對牛奶濃度0.8%的散射媒質分別靜置11,49和86 min后,我們將直徑40 mm,環厚1 mm的環狀光入射到散射媒質中,實驗結果如圖7(b)所示。隨著靜置時間的增長,散射媒質中的散射粒子逐漸沉淀,媒質容器中心部位的粒子濃度逐漸下降,散射波面的強度逐漸上升,中心的干涉波峰的大小也逐漸增大,旁瓣有逐漸向中心靠攏的趨勢。該實驗結果與計算解析結果呈現了相同的趨勢。雖然干涉波峰、旁瓣在位置、寬度上的一定的差異性,這是由于圖7(b)的實驗采用了不同參數的環狀光(環厚1 mm),同時該實驗結果出現時的濃度與計算結果上存在差異。通過計算可以知道,對于同樣大小的環狀光,在環厚比較細的情況下,更容易在近距離上相互干涉產生非衍射光[18]。相比于圖7(a)的計算結果,在圖7(b)的實驗中由于采用環厚更細的環狀光,在低于0.8 %濃度的散射介質中產生了中心干涉光,這符合理論依據。 圖6 環狀光在各濃度的散射媒質中的散射波形 (a)0.8%, (b)1.0%Fig. 6 Annular beam propagation pattern in random media at concentration of (a)0.8%, (b)1.0% 圖7 環狀光在各濃度散射媒質中波形的變化 (a)仿真結果;(b)實驗結果Fig. 7 Variation of annular beam propagation pattern in random media with different concentration (a) Simulation; (b) Experiment 然而在圖6中,依然可以看到理論計算與實驗結果在散射波形的旁瓣上存在的微小差別。這是因為受到多重散射的影響,波面在時間與空間上都會產生一定的波動,導致散射光在到達測量平面時相干性降低。而在本文中所討論的手法中我們假設了所有的光子都具有相干性、并沒有考慮到散射媒質的波動對散射光相干性的影響。所以在圖6(b)中,對相干性要求相對嚴格的旁瓣位置上,由于多重散射對相干性的影響,實驗結果的旁瓣波峰并不明顯。 本研究以幾何光學近似為基礎,運用迭代算法對環狀光在散射媒質中的傳播進行了數值分析。在單散射模型中,我們運用了簡化的幾何光學近似進行計算,其結果與米氏理論的散射結果一致,證明了該簡化幾何光學近似在散射計算中的可靠性。在此基礎上,運用迭代算法實現了多重散射的模型。通過透射率的計算,我們發現中心干涉光在散射媒質中出現時,散射媒質的濃度介于發生單一散射與多重散射的濃度之間。在環狀光散射波形的分析中,計算的散射波形的中心干涉波峰與旁瓣的振幅、位置與實驗結果一致。同時觀察到隨著沉淀過程的進行,散射波形變化的該過程與計算結果顯示了同樣的趨勢。隨著濃度的升高,中心干涉光波峰逐漸強度逐漸提高,旁瓣逐漸向中心位置移動。 在實際的應用中,若要利用環狀光在散射媒質中的該傳播特性,不僅需要調整散射媒質的濃度,其他光學參數(傳播距離、散射粒子的種類、大小、折射率、光源的調制形狀等)也需要相應的調整與控制。本文提出的基于幾何光學近似的迭代算法可以調整、控制相應參數,可在數值計算上優化環狀光在散射媒質中傳播效率,為實驗提供有效的理論依據。 若需完全構建與實驗條件相同的散射模型,在后續工作中需要在數值計算中加入散射媒質實時波動對干涉性的影響。同時運用該算法,探索在更高濃度的散射媒質中形成中心干涉光的條件。1.2 多重散射模型

2 解析結果
2.1 單散射模型計算結果評價

2.2 多重散射解析結果

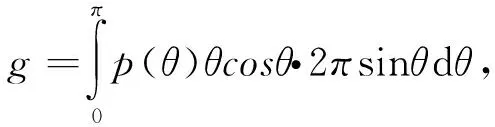
3 結論

