柱塞泵組件球面縫隙流動特性分析

陳旭峰， 高文科， 張繼銘

(蘭州理工大學 能源與動力工程學院， 甘肅 蘭州 730050)

引言

縫隙流動普遍存在于液壓元件等機械裝置，縫隙的大小和結構不僅決定流體介質的速度、壓力分布等特性，同時還與整機的工作性能密切相關。在縫隙的結構形式上，可分為平行平板間隙、傾斜平板間隙、圓柱環形間隙、漸縮及漸闊同心環形間隙、漸縮及漸闊偏心環形間隙、平行圓盤間隙、圓錐環形間隙、球面縫隙等。在柱塞泵中，球面縫隙是常見的縫隙結構之一，如在柱塞泵中柱塞球頭與滑靴球窩構成的間隙為球面縫隙；在某些球面配流副中，缸體端面和配流盤端面也構成球面縫隙。因此，針對球面縫隙結構分析其結構參數與流體介質流動特性之間的關系，對優化此類球面副的設計顯得尤為必要。

針對球面縫隙流動的研究，大多是從實際工程的角度出發，對某一具體結構進行研究，如柱塞泵中的球面配流副等[1-3]。王致清等[4]在考慮形成球面縫隙的兩元件有相同半徑的條件下，求出了考慮流動慣性時的球面間流體的壓力分布、速度分布以及泄漏流量的解析式。許賢良等[5]推導了具有相同半徑的球窩與球頭形成球面縫隙時，其間隙內流體流動的基本運動方程，并進一步推導了球面縫隙中流體的速度分布及壓力分布。陽恩會[6]對具有相同半徑的球頭與球窩形成球鉸副時，推導出了球鉸副靜態摩擦力矩的計算公式，并對球鉸副的支承特性和油膜剛度進行了分析。

針對柱塞泵球面配流副的研究，孟廣耀等[7]分析了球面配流與平面配流對柱塞泵的壓力流量脈動、空化等方面的影響。李小寧等[8]針對形成球面配流副的缸體端面和配流盤端面有相同的半徑時，對球面配流副的徑向反推力和反推力矩進行了求解，并得到了解析解。王偉[9]、向倫凱[10]在考慮配流盤球面和缸體球面有相同的半徑且其球心具有一定偏心時，對其間隙內流體的速度分布、壓力分布、泄漏流量及流體的承載量進行求解，并得出了相應的解析表達式。同時，在球面配流副中泄漏流量是衡量摩擦副潤滑效率的主要指標[11-14]。李小金等[15]推導出基于球面坐標系的貼體網格生成方程，在貼體坐標系下利用有限差分法迭代求解雷諾方程，得到了球面配流副的二維穩態壓力場。鄧海順等[16]在考慮形成球面配流副的缸體端面和配流盤端面有相同的半徑時，提出了球面配流副最佳平均間隙的概念，進一步完善了球面配流副的理論。

在球面配流副的大部分研究中忽略了球面配流的影響并將球面配流副簡化為平面配流副[17-20]。同時，關于球面縫隙流動的研究，在結構上大多是考慮形成球面縫隙的兩元件有相同的半徑且其球心存在一定的偏心時進行分析。但在實際工程中，很難保證形成球面間隙的兩元件有相同的半徑，如柱塞泵中柱塞球頭與滑靴球窩組成的球面縫隙，其通常要求滑靴球窩的半徑要略大于柱塞球頭的半徑，且在運行過程中滑靴球窩的球心相對于柱塞球頭的球心會發生一定的偏心。此外，如圖1所示，在形成球面縫隙的2個元件的結構的限制下，如果當0<θ1<π/2，π/2<θ2<π，并且2個元件的球心存在一定的偏心時，此時的兩元件不可能有相同的半徑。因此，文獻[5-10]、文獻[16]中所提供的結果僅適于計算0<θ1<θ2<π/2時的球面縫隙結構。

基于此，本研究從柱塞泵中所出現的球面縫隙機械結構出發(柱塞球頭與滑靴球窩構成的球鉸副以及球面配流副)，針對形成球面縫隙的兩元件存在不相等的半徑且球心發生一定的偏心時，對其縫隙中流體的速度分布、壓力分布、泄漏流量及流體的承載量進行建模，并以滑靴球窩與柱塞球頭構成的球面縫隙為例，分析其縫隙內流體的壓力分布、速度分布等特性。

1 縫隙間流體流動相關參數計算

球面縫隙流動常見于各種機械結構，如柱塞泵中的球面配流副，以及滑靴球窩與柱塞球頭構成的球鉸副等。在不同的機械結構中，流體到達球面縫隙的方式也有所不同。于是，可將各種滿足球面縫隙流動的機械結構簡化為如圖1所示的結構。由圖1可知，球A與B之間的球面縫隙中充滿了高壓油液，油液在高壓pr的作用下通過兩球面之間的間隙流出到外界(外界壓力為p0)，A與B均保持靜止，并且滿足0<θ1<90°，θ1<θ2<180°，其中θ表示密封帶相對于豎直方向的張角，其值位于θ1～θ2之間。

圖1 球面縫隙結構示意圖

A與B之間的油膜呈球形分布，此時宜采用球坐標系，如圖2所示。在球坐標系下，對于黏性不可壓縮流體，N-S方程如下：

(1)

式中，fr，fθ，fφ分別為r，θ，φ3個方向的單位質量力，fr=-gcosθ，fθ=gsinθ，fφ=0；ur，uθ，uφ分別為r，θ，φ3個方向的流體運動速度；p，ρ，μ分別為壓力、密度、動力黏度；dur/dt，duθ/dt，duφ/dt分別表示r，θ，φ3個方向的流體運動的加速度。

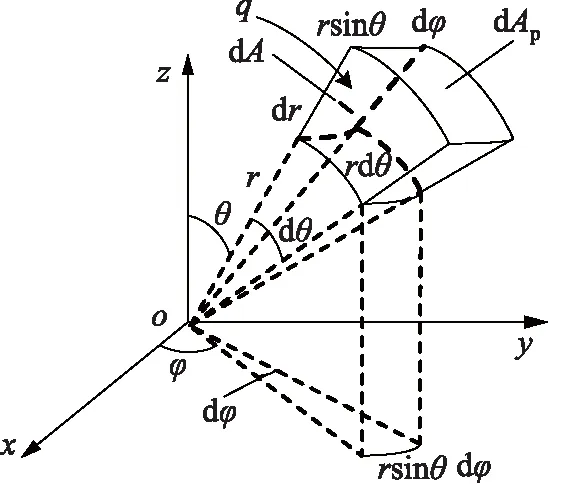
圖2 球坐標示意圖

對于精確求解N-S方程存在極大的困難。為此，根據球面縫隙流動的特點，其次通過比較各項的數量級，略去方程中的微小量，保留主要項，使得方程得到化簡。現將求解N-S方程的假設條件敘述如下：

(1) 油液為牛頓流體，并忽略油液質量力的作用。油液流動為層流，油膜中不存在湍流，與黏性力相比可忽略油液慣性力的作用，包括流體加速時的力和油膜彎曲的離心力；

(2) 油液充滿整個球面縫隙，在固體表面上油液無滑動，即貼于固體表面的油液流速與表面速度相同；

(3) 在沿著油膜厚度方向(即r方向)上忽略油液壓力的變化，即?p/?r=0。由于膜厚僅為百分之幾毫米或更小，因此壓力不可能發生明顯的變化；

(4) 在球面縫隙流動中，uθ為主要的速度分量，其他速度分量uφ=ur=0；

(5) 由于球面縫隙流動關于z軸對稱，因此各流動參數與φ無關，即?/?φ=0。

基于上述假設，則N-S方程可化簡為：

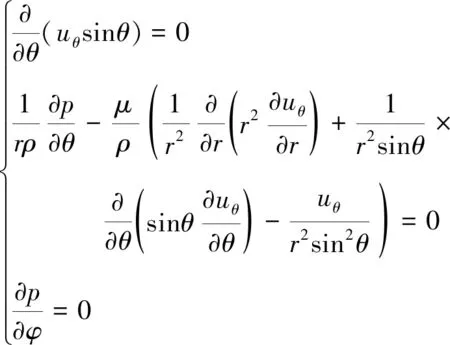
(2)

對式(2)中第一式，可等價化簡為：

(3)

于是，將式(3)代入式(2)中第二式，則：

(4)

根據假設(3)及假設(5)可知，p與r，φ均無關，則?p/?θ=dp/dθ。對式(4)進行積分，則：

(5)

實際上在工程問題中，形成球面縫隙的A與B很難保持同心，往往存在一定的偏心e。同時，由于存在加工精度及配合等問題，也很難保證A與B有相同的半徑，對于A與B的相對位置，如圖3所示。

由圖3可知，當偏心e>0時，隨著θ的增大，油膜厚度逐漸減小，油膜在θ方向上呈漸縮狀態；當偏心e=0時，油膜厚度恒為定值；當偏心e<0時，隨著θ的增大，油膜厚度逐漸增大，油膜在θ方向上呈漸闊狀態。

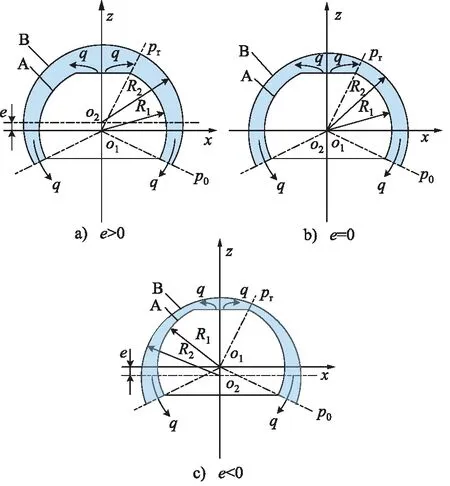
圖3 球面縫隙結構相對位置示意圖

如圖1所示，在三角形o1o2D中，|o1o2|=e，|o1D|=H，|o2D|=R2，|o1C|=R1，于是根據余弦定理則有：

(6)

于是，解得H為：

(7)

通常e/R2?1，因此忽略高階微量，則：

H=R2+ecosθ

(8)

因此，球面縫隙尺寸(或油膜厚度)為：

h=|CD|=H-R1=R2-R1+ecosθ

(9)

令δ=R2-R1，則：

h=δ+ecosθ

(10)

如圖1所示，考慮其本身機械結構，即在任意θ處，油膜厚度h均大于0，則當θ=θ1時，h>0；當θ=θ2時，h>0。代入式(10)，則半徑間隙δ與偏心距e的關系式為：

δ+ecosθ1>0

δ+ecosθ2>0

(11)

根據邊界條件(假設(2))，當r=R1時，uθ=0，當r=H時，uθ=0，則解得油液流速uθ為：

(12)

如圖2所示，在球坐標系中，在r，θ處的微元面積dA=rsinθdφdr，則流過微元面積dA的微元流量dq為：

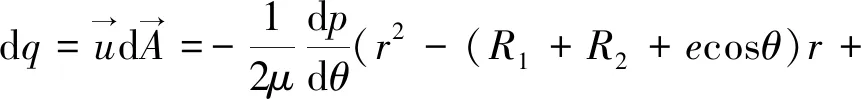
R1(R2+ecosθ))sinθdφdr

(13)

對式(13)進行積分得：

(14)

考慮到在微元面積dA處，流速uθ的方向與微元面積dA的外法線方向相反，因此此時計算出的總泄漏流量q為負值。于是，在整個球面縫隙中，流量數值大小為：

Q=-q

(15)

令ε=e/δ，根據式(8)，則ε的取值范圍為：

1+εcosθ1>0

1+εcosθ2>0

(16)

在柱塞球頭與滑靴球窩構成的球鉸副中，通常滿足0<θ1<π/2且π/2<θ2<π時，此時cosθ1>0且cosθ2<0，則有-secθ1<ε<-secθ2，此時由于機械結構所限，ε既有下確界又有上確界。

于是，將式(11)變換成dp的微分式，并將式(10)代入，則：

(17)

對式(17)進行積分，并代入壓力的邊界條件，即當θ=θ1時，p=pr；當θ=θ2時，p=p0，則解得壓力分布p及流量數值大小Q分別為：

(18)

(19)

令：

(20)

式(20)中，Kq僅與θ1，θ2及ε有關，其中θ1與θ2表示在結構上A與B構成的球面縫隙的尺度大小，ε表示在結構上A與B球心的偏心程度。從而，Kq僅由A與B的幾何尺寸以及A與B的相對偏心程度所唯一確定，Kq可稱為球面縫隙流動中的球面支撐泄漏系數。

則：

(21)

由球面縫隙中油液壓力的表達式，可求得壓力對θ的梯度為：

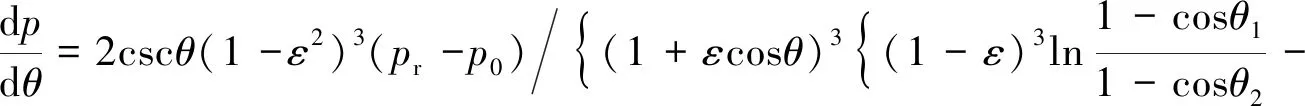
(22)

將式(22)代入式(12)，則球面縫隙內油液的速度分布為：

(23)

2 油膜承載量分析

如圖2所示，在球A面上微元面積dAp可表示為(圖2中r取R1):

(24)

因此，球面縫隙中油液作用于A上微元面積dAp的作用力可表示：

dFp=pdAp

(25)

將dFp分別沿著水平方向及z方向分解，則：

dFr=psinθdAp

(26)

dFz=pcosθdAp

(27)

因此，球面縫隙中油液作用于球A面上的總的作用力(或油膜的承載量)為：

(28)

(29)

由于球面縫隙流動關于z軸對稱，因此Fr=0，Fz可進一步表示為：

(30)

將式(18)代入式(30)，則：

(31)

式(31)中，相關積分可積得：

(32)

將J1，J2,J3,J4及J5分別代入式(31)，則：

(33)

令：

(34)

式(34)中，KF是僅與θ1,θ2及ε有關的結構常數。從而，KF僅由A與B的幾何尺寸以及A與B的相對偏心程度所唯一確定，KF可稱為球面縫隙流動中的球面支撐承載系數。

則：

Ⅰ：如果當球A與B的半徑相等，即R1=R2=R時，此時δ=R2-R1=0，代入式(18)、式(19)、式(23)及式(33)，則球面縫隙中油液的壓力分布、流量、流速分布以及油膜承載量分別為：

(36)

(37)

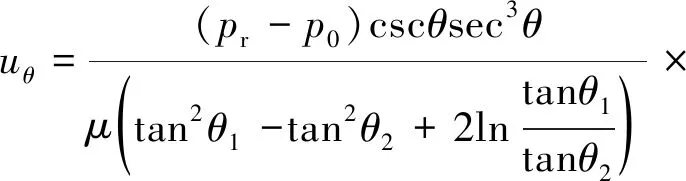
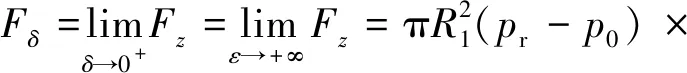
(39)

式(36)～式(39)中，須滿足0<θ1<θ2<π/2，這是由于當A與B的半徑相等時，此時A與B若存在一定的偏心e，則在其結構本身的限制下，θ1與θ2不可能大于π/2。在球面配流副中，通常滿足0<θ1<θ2<π/2，因此在粗略計算其相關參數時，可假定A與B的半徑相等，進而進行計算。

Ⅱ：如果當球A與B的偏心距e=0時，代入式(18)、式(19)、式(23)及式(33)，則球面縫隙中油液的壓力分布、流量、流速分布以及油膜承載量分別為:

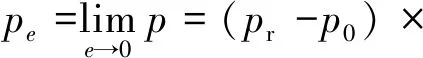
(40)

(41)

(42)

(43)

在滑靴球窩與柱塞球頭構成的球面縫隙中，通常滿足0<θ1<π/2且π/2<θ2<π。因此，在粗略計算某些球面縫隙流動相關參數或在某些特殊場合時，可忽略A與B球心的偏心距e，進而進行計算。

3 實例分析

考慮到球面縫隙流動常見于各種機械結構，如柱塞泵中的球面配流副以及滑靴球窩與柱塞球頭構成的球鉸副等，但在不同的球面副中，其相關參數的計算形式略有差異。因此，本研究僅以滑靴球窩與柱塞球頭構成的球鉸副進行實例分析。

某型號柱塞泵的滑靴與斜盤摩擦副設計成如圖4所示的靜壓支承。設柱塞阻尼孔直徑d=0.4 mm，阻尼孔長度l=25 mm，通過柱塞阻尼孔時壓降系數α=pr/ps=0.9；泵的工作壓力ps=32 MPa，泵殼內的壓力p0=0，油液的動力黏度μ=8.7×10-3Pa·s；柱塞球頭半徑R1=7.49 mm，滑靴球窩半徑R2=7.5 mm，滑靴球頭球心相對于滑靴球窩球心的偏心距離e=2 μm，角度θ1=8°，θ2=140°；滑靴底部半徑r1=7.5 mm，r2=11 mm；(假設滑靴球窩θ≤θ1范圍內的壓力與滑靴底部r≤r1范圍內的壓力相同(即忽略滑靴阻尼孔的壓力損失)，均為pr)。

圖4 柱塞-滑靴示意圖

通過柱塞阻尼孔的流量為：

(44)

引入阻尼孔泄漏系數：

(45)

則：

(46)

由式(21)，通過滑靴球窩與柱塞球頭流出的流量為：

(47)

通過滑靴底部與斜盤間縫隙流出的流量為：

(48)

引入平行圓盤支撐泄漏系數：

(49)

則：

(50)

通過柱塞細長阻尼孔的流量qr一部分通過滑靴自身的阻尼孔到達滑靴底部，另一部分通過滑靴球窩與柱塞球頭構成的球面縫隙流出到泵殼內。因此，根據流量的連續性方程，則qr=q1+q2。

代入相關數據，解得Kqr=2.5133×10-14，Kq1=0.1671，Kq2=1.3671。于是，解得通過柱塞細長阻尼孔的流量為qr=554.65 mL/min，通過滑靴球窩與柱塞球頭流出的流量為q1=33.18 mL/min，通過滑靴底部與斜盤間的縫隙流出的流量為q2=521.47 mL/min，進而解得滑靴底部與斜盤形成靜壓支撐的油膜厚度h=12.43 μm。

特殊地，若忽略滑靴球窩相對于柱塞球頭的偏心，即假設e=0，則根據式(41)，解得通過滑靴球窩與柱塞球頭流出的流量為q1=28.33 mL/min，而當偏心距e=2 μm時，q1=33.18 mL/min。因此，此時忽略偏心時所計算的泄漏流量誤差為14.62%。

3.1 滑靴球窩內相關參數實例分析

在滑靴球窩與柱塞球頭構成的球面縫隙中，仍假設各參數為ps=32 MPa，θ1=8°,θ2=140°，pr=αps=28.8 MPa，R1=7.49 mm，R2=7.5 mm。根據式(21)，則ε的取值范圍為(-1.0098,1.3054)，從而偏心距e的取值范圍為(-10.10,13.05)。根據式(10)、式(18)、式(19)以及式(33)，繪制出不同ε時，油膜厚度h、壓力分布p、流量Q、油膜承載量Fz的函數圖像，如圖5～圖8所示。當偏心距e=2 μm時，根據式(23)，繪制出球面縫隙中油液流速uθ隨θ及r的函數圖像，如圖9及圖10所示。

由圖5可知，當ε<0時，隨著ε的增大，油膜厚度h逐漸增大，油膜在θ方向上呈漸闊狀態；當ε=0時，油膜厚度h恒為定值，且h=δ；當ε>0時，隨著ε的增大，油膜厚度h逐漸減小，油膜在θ方向上呈漸縮狀態。

由圖6可知，當ε<0時，壓力曲線整體位于ε=0

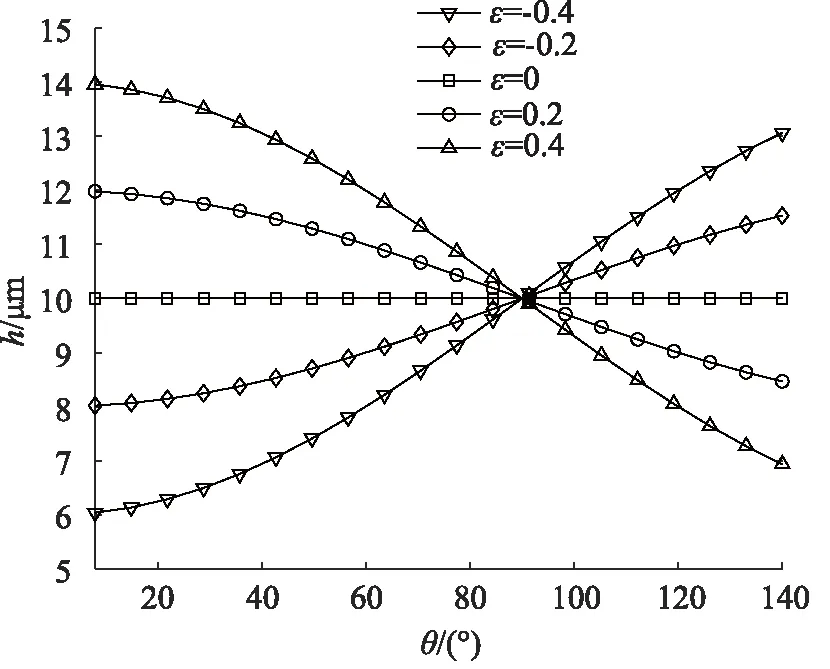
圖5 不同ε下的油膜厚度分布

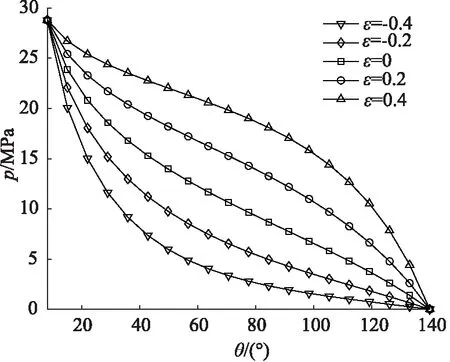
圖6 不同ε下的油液壓力分布

圖7 不同ε下的泄漏流量

時的壓力曲線下側；當ε>0時，壓力曲線整體位于ε=0時的壓力曲線上側。

由圖7可知，隨著ε的增大，流量Q先增大后減小，且當ε=0.2732時，流量Q達到最大值Qmax=33.59 mL/min。

由圖8可知，隨著ε的增大，承載量Fz先增大后減小，且當ε=0.5952時，承載量Fz達到最大值Fz max=3078.37 N。

圖8 不同ε下的油膜承載量

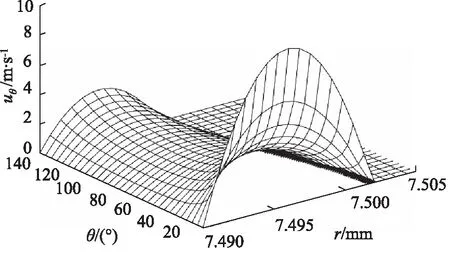
圖9 流速分布曲面圖

圖10 流速分布曲線圖

由圖9、圖10可知，當張角θ一定時，球面縫隙中油液流速uθ在油膜厚度方向(即r方向)上呈拋物線分布。

4 結論

(1) 從柱塞泵中所出現的球面縫隙機械結構出發(柱塞球頭與滑靴球窩構成的球鉸副以及球面配流副)，針對形成球面縫隙的兩元件存在不相等的半徑且球心發生一定的偏心時，對其縫隙中流體的速度分布、壓力分布、泄漏流量及流體的承載量進行了求解，并得到了其解析表達式。同時，得到了僅與球面縫隙流動其自身結構有關的球面支撐泄漏系數Kq和球面支撐承載系數KF；

(2) 通過本研究所推導的式(18)、式(19)、式(23)、式(33)可直接導出當兩元件存在相等的半徑且球心發生一定的偏心時，其縫隙內流體相關參數的表達式，如式(36)～式(39)，這與文獻[5-10]、文獻[16]中所提供的相應結果完全一致。同時，通過式(18)、式(19)、式(23)、式(33)也可推導出當兩元件存在不相等的半徑且忽略球心的偏心時，其縫隙內流體相關參數的表達式，如式(40)～式(43)所示；

(3) 以滑靴球窩與柱塞球頭形成的球鉸副為例，對其球面縫隙中油液的速度分布、壓力分布、泄漏流量及油膜承載量等進行了求解，并進行了數值分析。對于滑靴球窩與柱塞球頭之間泄漏流量的精確求解，可進一步為滑靴底部與斜盤表面間油液的承載量、泄漏流量、油膜剛度等參數的研究提供進一步的參考。

在實際工況中很難保證形成球面縫隙的兩元件有相同的半徑，因此通過更為精確的求解其縫隙內流體相關參數的分布，可進一步為相關形成球面縫隙的機械結構(如柱塞泵中的球面配流副滑靴球窩與柱塞球頭構成的球鉸副等)設計提供理論依據。