全平面上含混合核的Hilbert 型不等式及應用
2021-04-26 02:38:30有名輝范獻勝何振華
韶關學院學報 2021年3期
關鍵詞:浙江
有名輝,范獻勝,何振華
(1.浙江機電職業技術學院 數學教研室,浙江 杭州 310053;2.廣西財經學院 信息與統計學院,廣西 南寧 530003)

其中c0=0.915 9…為Catalan 常數[2]. 2013 年,陳小雨等研究了式(4)的非齊次情形,并給出了參數推廣[3].另外,劉瓊研究了式(4)的推廣[4]. 與式(3)和式(4)的相關聯的其他文獻可參照文獻[5-8].值得指出的是,在Hilbert 型不等式誕生后的百余年間,通過不斷創新核函數,研究者們還給出了大量新的Hilbert 型不等式[9-20]. 本文將建立含有新核的全平面上的Hilbert 型不等式,即:
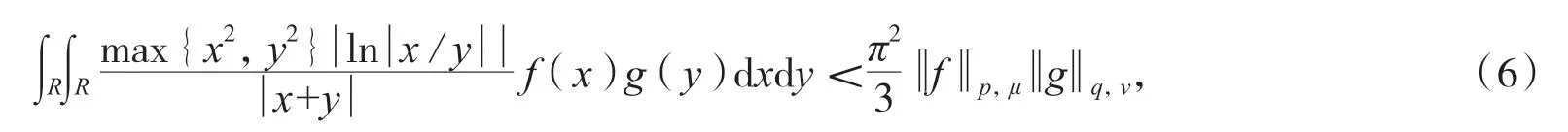
其中μ(x)=|x|2p-1,v(y)=|y|q-1.更一般地,筆者將構建多參數的積分核函數,建立式(5)、式(6)的推廣形態,首先給出若干引理.
1 引理
引理1設γ>0,λ≥0,β1,β2>-λ,β1+β2=2n-λ+1. 且有:

將式(15)代入式(10),可得式(8).同理可得式(9).
引理2設γ>0,λ≥0,β1,β2>-λ,β1+β2=2n-λ+1. k(x,y)及C(β1,β2,λ,γ,n)由引理1 定義. ε 是充分小的正數,則當ε →0+時,有:
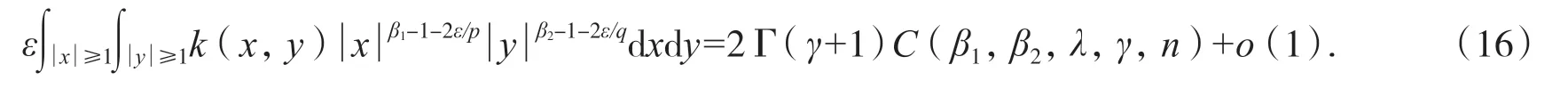

由此可知引理3 成立.
2 主要結果


3 推論


猜你喜歡
考試與評價·高二版(2021年5期)2021-09-10 07:22:44
非公有制企業黨建(2020年9期)2020-09-26 13:22:18
學生天地(2019年30期)2019-08-25 08:53:22
瘋狂英語·新策略(2018年1期)2018-08-20 07:50:38
領導決策信息(2017年13期)2017-06-21 10:10:36
領導決策信息(2017年12期)2017-05-17 04:49:18
喜劇世界(2017年5期)2017-03-29 01:52:25
中國衛生(2016年7期)2016-11-13 01:06:44
杭州(2015年9期)2015-12-21 02:51:52
中國衛生(2014年10期)2014-11-12 13:10:10

