巧用定義 數(shù)形結(jié)合
——絕對(duì)值的幾何意義在最值問題中的應(yīng)用
賴 倩
(重慶南開兩江中學(xué)數(shù)學(xué)組 重慶 401135)
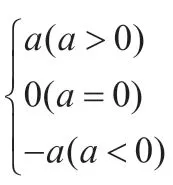
當(dāng)出現(xiàn)多個(gè)絕對(duì)值的時(shí)候,利用絕對(duì)值的代數(shù)定義去掉絕對(duì)值的“零點(diǎn)分段法”是解決此類問題的主要方法.零點(diǎn)分段法分為找零點(diǎn),分區(qū)間,定符號(hào),去絕對(duì)值符號(hào)這幾個(gè)基本步驟,注意有n個(gè)絕對(duì)值的式子就有n個(gè)零點(diǎn),就會(huì)把數(shù)軸分成n+1,題目就會(huì)分n+1種情況來討論.
例如:求出滿足|2x-4|+|3x+1|=5的x的值.
我們接著來看以下的這個(gè)例子:
請(qǐng)回答
(1)若|x-2|+|x+1|=3,則x 能取到的最小值是__________,最大值是___________;
(2)滿足|x-2|+|x+1|=2的x有_____個(gè);
(3)滿足|x-2|+|x+1|=6的x有_____個(gè),值為_____;
(4)當(dāng)|x-2|+|x+1|+|x+3|取最小值時(shí),則x的值為__________;
(5)|x-1|+|x-2|+…|x-1 9 9 7|的最小值為____________________.
此題考察的含有絕對(duì)值的代數(shù)式的最值問題,當(dāng)然可以用我們前文提到的“零點(diǎn)分段法”來解答,這里就不再贅述.
數(shù)軸上表示數(shù)a的點(diǎn)與原點(diǎn)的距離叫做數(shù)a的絕對(duì)值,這既是絕對(duì)值的定義又是絕對(duì)值的幾何意義.數(shù)軸上表示數(shù)a的點(diǎn)與表示數(shù)b的點(diǎn)的距離記作|a-b|,例如|3-5|表示數(shù)軸上表示數(shù)3的點(diǎn)與表示數(shù)5的點(diǎn)的距離,|3+5|=|3-(-5)|表示數(shù)軸上表示數(shù)3的點(diǎn)與表示數(shù)-5的點(diǎn)的距離,|a-3|表示數(shù)軸上表示數(shù)a的點(diǎn)與表示數(shù)3的點(diǎn)的距離.接下來,我們將緊緊抓住絕對(duì)值的幾何意義,利用數(shù)形結(jié)合的思想,巧妙的解決這種最值問題.
如本題,當(dāng)兩個(gè)絕對(duì)值里面x的系數(shù)是±1或者說能同時(shí)調(diào)整為±1的時(shí)候,利用絕對(duì)值的幾何意義,單個(gè)絕對(duì)值|x-2|可以看做數(shù)軸上表示數(shù)x的點(diǎn)到2的距離,|x+1|可以看做數(shù)軸上表示數(shù)x的點(diǎn)到-1的距離,那么整個(gè)式子就可以翻譯為數(shù)軸上表示數(shù)x的點(diǎn)到2和到-1兩點(diǎn)的距離之和.

我們利用數(shù)軸把題目當(dāng)中涉及到的數(shù)表示出來,利用數(shù)形結(jié)合,可以看到當(dāng)點(diǎn)在-1和2之間(即點(diǎn)在圖中線段AB上,包含端點(diǎn))的時(shí)候,到兩點(diǎn)的距離之和就是這兩個(gè)定點(diǎn)之間的距離即為AB=|-1-2|=3;當(dāng)點(diǎn)在線段AB之外(即在-1的左邊或者2的右邊)的時(shí)候,到兩點(diǎn)的距離之和就會(huì)大于這兩個(gè)定點(diǎn)之間的距離;并且離這兩個(gè)點(diǎn)的距離越遠(yuǎn),這個(gè)值越大.用符號(hào)語言來描述上述的結(jié)論就是:|X-2|+|X+1|≥3(當(dāng)且僅當(dāng)-1≤x≤2時(shí)等號(hào)成立).
則此題(1)答案為:若|x-2|+|x+1|=3,則x能取到的最小值是 -1 ,最大值是 2 .
拓展可解決以下問題:滿足|x-2|+|x+1|=2的x有_______個(gè);
從前面的分析可以知道,數(shù)軸上的點(diǎn)到這兩個(gè)定點(diǎn)之和的最小值就是這兩個(gè)定點(diǎn)之間的距離,而本題兩個(gè)定點(diǎn)之間的距離為3,現(xiàn)在2<3,∴在數(shù)軸上是找不到任何點(diǎn)使得該式子成立的,故答案為0個(gè).
(3)滿足|x-2|+|x+1|=6的 有_______個(gè),值為_______;
同前分析,∵6>3∴在數(shù)軸上是找得到這樣的點(diǎn)使得該式子成立的.那么這樣的點(diǎn)有幾個(gè)呢?易得,這樣的點(diǎn)一定在線段AB之外,我們不妨先來看看當(dāng)點(diǎn)在-1的左側(cè)的時(shí)候,如下圖1
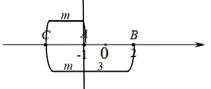
圖1
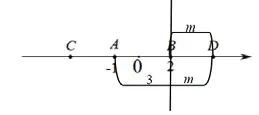
圖2
∵2m+3=6 ∴m=1.5 ∴x=-1-1.5=-2.5
而且通過觀察可以發(fā)現(xiàn),如圖2,當(dāng)在線段之外與這兩個(gè)定點(diǎn)的距離相同的點(diǎn)呈現(xiàn)出對(duì)稱性的性質(zhì),即CA=BD時(shí),C、D兩點(diǎn)對(duì)應(yīng)的數(shù)帶入這個(gè)式子,到兩個(gè)定點(diǎn)的距離之和是相等的.∴x=2+1.5=3.5
由此,滿足|x-2|+|x+1|=6的x有 2 個(gè),值為 x=-2.5或x=3.5 .
本題的(4)問當(dāng)|x-2|+|x+1|+|x+3|取最小值時(shí),則x的值為__________;
絕對(duì)值增加到了3個(gè),根據(jù)前面的分析是數(shù)軸上表示x的點(diǎn)到-3,-1,2這三個(gè)定點(diǎn)的距離之和.

我們知道,x要放在定點(diǎn)的中間,這個(gè)距離之和的值就最小,但是此時(shí)還有與第三個(gè)定點(diǎn)的距離,那放到哪兩個(gè)定點(diǎn)的中間就需要思考和取舍了,經(jīng)分析,x要放在最外面的兩個(gè)定點(diǎn)的中間,即當(dāng)-3≤x≤2時(shí),x到-3,2這兩個(gè)定點(diǎn)的距離之和就是這兩個(gè)定點(diǎn)的距離即為|-3-2|=5,此時(shí)還需要考慮|x+1|即與-1的距離,也要盡可能小才行,此時(shí)x恰好可以取到-1,使得|x+1|=0,而這個(gè)值恰好是絕對(duì)值的最小值,兩個(gè)部分都取到了最小值,而且最小值成立的條件是可以同時(shí)成立的,問題得到解決,即|x-2|+|x+1|+|x+3|≥5+0=5(當(dāng)且僅當(dāng) 時(shí)等號(hào)成立).
可能有同學(xué)會(huì)思考,x為什么不能放在-3與-1之間或者-1與2之間呢?其實(shí)也是可以的,我們不妨以在-3與-1之間為例,當(dāng)-3≤x≤-1時(shí),|x+1|+|x+3|≥2,那么剩下的第三個(gè)絕對(duì)值|x-2|在x=-1時(shí),與2最近,|x-2|≥+-1-2+=3,∴|x-2|+|x+1|+|x+3|≥2+3=5(當(dāng)且僅當(dāng)x=-1時(shí)等號(hào)成立).
兩種方法得到的答案和最小值成立的點(diǎn)都是相同的,但是當(dāng)絕對(duì)值的數(shù)量進(jìn)一步增大的時(shí)候,第一種思路會(huì)更加方便.
即當(dāng)|x-2|+|x+1|+|x+3|取最小值時(shí),則x的值為 x=-1 ;
(5)|x-1|+|x-2|+…+|x-1 9 9 7|的最小值為____________________.
這一問的難度就非常大了,一下子拓展到了1997個(gè)絕對(duì)值的和,乍一看到,很多學(xué)生是會(huì)無從下手的,需要學(xué)生很強(qiáng)的綜合能力.但如果學(xué)生能充分理解絕對(duì)值的幾何意義,掌握好前面幾個(gè)小問的處理方法之后,這個(gè)題目也是可以變得相對(duì)簡(jiǎn)單的.整個(gè)題目可以翻譯為數(shù)軸上表示x的點(diǎn)到1,2,…,1997這1997個(gè)距離之和.最根本的想法就是讓點(diǎn)越往中間走值越小,這1997個(gè)數(shù)字,有正中間的一個(gè)數(shù)999,那么當(dāng)x=999時(shí),整個(gè)式子的值最小,最小值為2×(1+2+3+…+998)=997002.
即|x-1|+|x-2|+…+|x-1997|的最小值為 997002 .
這里可以給大家留下幾個(gè)思考題,參考以上的方法和思路可以得到極大的簡(jiǎn)化.
補(bǔ)充1:若|b+2|+|a-5|=4-|a-3|-|b+1|,求ab的最大值.
補(bǔ)充2:求|x-2|+2|x+1|+3|x+3|的最小值.
補(bǔ)充3:一條直街上有5棟樓,按從左至右順序編號(hào)為1、2、3、4、5,第k號(hào)樓恰好有k(k=1、2、3、4、5)個(gè)A廠的職工,相鄰兩樓之間的距離為50米.A廠打算在直街上建一車站,為使這5棟樓所有A廠職工去車站所走的路程之和最小,車站應(yīng)建在距1號(hào)樓____米處.
補(bǔ)充4:已知(|x+1|+|x-2|)(|y-2|+|y+1|)(|z-3|+|z+1|)=36,求x+2y+3z的最大值和最小值.
補(bǔ)充5:如圖,點(diǎn)O為數(shù)軸上的原點(diǎn),點(diǎn)A、B分別為數(shù)軸上兩點(diǎn),對(duì)應(yīng)的數(shù)分別為a、b,已知a=10,AB=3AO.
(1)若動(dòng)點(diǎn)P從點(diǎn)O出發(fā),以1個(gè)單位長(zhǎng)度/秒的速度沿?cái)?shù)軸正方向勻速運(yùn)動(dòng),同時(shí)動(dòng)點(diǎn)Q從點(diǎn)B出發(fā)以v個(gè)單位長(zhǎng)度/秒的速度沿?cái)?shù)軸負(fù)方向勻速運(yùn)動(dòng),經(jīng)過8秒時(shí),PQ=16.求v的值;

當(dāng)然,我們利用絕對(duì)值的來表示距離的應(yīng)用,不僅可以處理距離之和的最值問題,也可以處理距離之差的最值問題,例如:當(dāng)|x-2|-|x+1|取最大值時(shí),則x的取值范圍是____________.
到兩個(gè)定點(diǎn)的距離之差和到兩個(gè)定點(diǎn)的距離之和這兩種題型之間既有區(qū)別又有聯(lián)系,大家可以利用上述思路去體會(huì)一下,同樣是可以巧用絕對(duì)值的幾何意義,數(shù)形結(jié)合,簡(jiǎn)化難度,解決題目的.
上文所提到的幾個(gè)例子由淺入深,層層遞進(jìn),讓我們可以通過這些例子充分體會(huì)到絕對(duì)值的幾何意義在此類最值問題中的重要運(yùn)用,使用得當(dāng)可以極大的降低這些最值問題的難度,會(huì)讓這類學(xué)生看起來復(fù)雜且無從下手的絕對(duì)值相關(guān)的最值題目變得簡(jiǎn)單,希望大家可以在日常教學(xué)中充分的講解絕對(duì)值的幾何意義,滲透這種數(shù)形結(jié)合的思想,讓學(xué)生能夠突破難點(diǎn),掌握此類問題的解題技巧,也能在此過程中體會(huì)到定義學(xué)習(xí)的重要性.

