初高中數學教學銜接研究
——從一道高一期末考試二次函數壓軸題談起

尚洪壩 張 俊

（重慶市酉陽第一中學校 重慶酉陽 409800）

如何銜接好初高中數學教學，是提高高中數學教學質量一個十分緊迫的問題。二次函數是中學數學中最基本的簡單的函數類型，也是初高中數學教材中聯系最為密切的內容之一。怎樣以初中所學知識為切入點，做好初高中銜接就成了一線教師亟待解決的問題，本文以一道高一期末考試二次函數壓軸題為例，談談怎樣發揮二次函數的潛在價值，讓初高中數學銜接更自然有效。

重慶市高2022屆高一上期期末考試第21題：

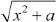
（1）當a＜0 時，求f(x)的值域；

（2）若存在x0∈R使得f(x0)＜0成立，求a的取值范圍。

=2t2-8at-a=2(t-a)2-8a2-a，由a＜0，

∴f(x) =g(t)=2(t-a)2-8a2-a

在t∈［0，+∞）上單調遞增，∴f(x)的值域為［-a，+∞）。

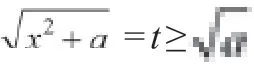
對稱軸方程t=2a，

本題的實質是考查學生對二次函數性質的應用。要求學生具備抓住二次函數開口方向、對稱軸與二次函數單調性的關系以及將存在性問題轉化為求函數的最值問題的能力，另外，還應具備換元及分類討論的思想方法。這個題目作為期末考試壓軸題，對于絕大多數高一學生來說，無疑是很艱難的。它首先需要利用換元、整體代換的思想方法將這個函數轉化為一個標準的含參的二次函數表達式。因此，在求函數的最值問題上不是簡單的看函數的單調性，還需考慮新函數的定義域，也需討論函數對稱軸與區間的關系。這道題基本涵蓋了我們處理二次函數問題所涉及的所有知識，綜合性較強。

在初中我們學習了二次函數的概念、圖象及一些簡單的性質。對一些題型如用待定系數求二次函數的解析式，用配方法或者對稱軸求解二次函數在R上的最值也掌握得不錯。而進入高中的學習之后，二次函數的內容穿插在各章節之中。主要考查定義域、值域、單調性、奇偶性、最值、函數在某一區間根的分布情況、二次函數與一元二次方程，以及一元二次不等式之間的關系等。對不含參數的二次函數在局部區間上求函數的單調性、最值也多有涉及。但像本題一樣借助換元法、分類討論及數形結合思想對函數本身進行轉化為通過動軸動區間的最值討論求字母參數的題目的確少有研究。因此，在整個討論過程中學生是很痛苦的。這必須要求學生對二次函數圖象和性質具備更為深刻的理解，而非停留在簡單的記憶和套用上。存在性問題轉化為函數的最值問題進行探討，具有一定的隱密性和復雜性的特征。當然這對學生知識遷移跟應用能力要求較高，對于一般的學生來說難以及時掌握。這就勢必造成了初中教學與高中教學的脫節。許多學生就會產生抵觸乃至厭學心理，導致高中數學成績直線下降。因此，做好初高中教學銜接是非常有必要的。

從本題而言，二次函數教學上應做好三點銜接。一是知識方面的銜接。相當部分高一學生已會配方法，也會討論定值定區間的最值了，但對動軸定區間、定軸動區間、動軸動區間問題的討論還很陌生。應引導學生學會熟練做草圖，運用動態的眼光觀察指定區間上的最值。二是思想方法上的銜接，本題從宏觀上講，首先要有整體代換的換元思想，其次要有區間與對稱軸位置的分類討論思想，還要有將存在性問題轉化成單變量最值問題的等價思想，也要有“以形助數”的數形結合思想。應引導學生體會這其中的變與不變的根本和關系。這將是對學生充分應用數學知識解決實際問題的能力的培養。學生在這個過程的接受能力也許有限，教師不要急于求成，要在平常的學習中加強訓練，多刺激學生深刻透徹的理解二次函數，掌握基本題型的求解方法。學生在這個過程中能力得到了提升，視野得到了開拓，這必將有效的促進初高中教學銜接。三是心理上的銜接。在初中階段，學生學習過二次函數，容易產生輕視感與疲勞感，認為二次函數簡單，只需復習鞏固就可考高分。很顯然，這是一種僥幸心理，導致的后果必然是一聽就懂，一做就錯。因此，在教學中，應特別強調高中二次函數學生的重要性與艱巨性，認清初中學習的二次函數函數內容跟高中的本質區別，為學生指明高中學習的方向與目標。

總之，為了學生更好地適應新課改下的數學教學要求，教師必須立足于當下學生所掌握的內容，樹立初高中數學教學銜接的重要意識，做好初高中數學教學銜接。