基于虛擬介質(zhì)方法數(shù)值模擬應(yīng)力波穿透水艙

史汝超， 孫曉旺

(1.江蘇海洋大學(xué) 理學(xué)院，江蘇 連云港 222005；2.連云港中復(fù)連眾復(fù)合材料集團(tuán)有限公司，江蘇 連云港 222023； 3. 南京理工大學(xué) 機(jī)械工程學(xué)院，南京 210094)

水艙是艦艇的常見裝置，可分為壓載水艙、補(bǔ)重水艙、間歇水艙等多種專用水艙。應(yīng)力波穿透水艙是一個(gè)典型的流固耦合問題，常見于艦艇的防護(hù)設(shè)計(jì)和抗爆抗沖擊研究[1-3]。目前，數(shù)值模擬該類問題較常使用的方法是SPH(smoothed particle hydrodynamics)[4]和ALE(arbitrary-Lagrangian-Eulerian)方法[5]。這兩種方法適用性很廣，因此，大部分主流商業(yè)軟件，如ANSYS、Abaqus等，都是基于這兩種方法開發(fā)的。然而，如果想非常精確地求解并刻畫固體中的應(yīng)力波，很多時(shí)候需要使用數(shù)值精度較高的有限差分法，選擇特定的差分格式，并設(shè)以特定的時(shí)間步長和空間網(wǎng)格。目前，完全使用有限差分法處理流固耦合問題的計(jì)算方法是虛擬介質(zhì)方法[6-7]。

虛擬介質(zhì)方法可進(jìn)一步細(xì)分為OGFM法則(original ghost fluid method)[8]、MGFM法則(modified ghost fluid method)[9]和RGFM法則(real ghost fluid method)[10]。收斂性較好的是MGFM法則和RGFM法則，均已初步推廣至水下沖擊波沖擊流固界面問題，可獲得很好的模擬效果[11-13]。本文進(jìn)一步以MGFM法則為基礎(chǔ)，將虛擬介質(zhì)方法推廣至固體應(yīng)力波在流固界面處的折射問題，并以此為基礎(chǔ)，數(shù)值模擬應(yīng)力波穿透水艙。

1 虛擬介質(zhì)方法

1.1 流體控制方程

二維軸對(duì)稱歐拉方程可寫為

(1)

其中，

(2)

(3)

(4)

(5)

式中:ρ為密度；p為壓力；u，v，w為x，y，z方向的速度;r為任一點(diǎn)至y軸的距離；單位質(zhì)量總能E=ρ(u2+v2+w2)/2+ρe。對(duì)于一維問題，式(1)可簡化為

(6)

1.2 固體控制方程

取壓應(yīng)力為負(fù)值、拉應(yīng)力為正值。固體的二維軸對(duì)稱彈性動(dòng)力學(xué)方程可寫為

(7)

其中，

(8)

(9)

(10)

(11)

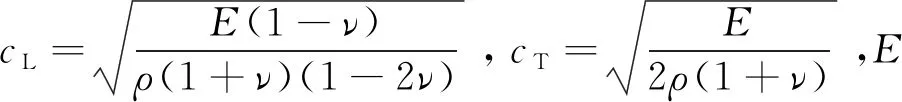
(12)

1.3 近似黎曼解算器

流固界面在數(shù)學(xué)上屬于黎曼問題。圖1 給出了求解黎曼問題的特征線法示意圖。在流固界面處沿特征線差分，可得到界面處的差分近似解。圖中固體設(shè)定在界面左側(cè)，故取右特征線方程

dσ-ρcdu=0

(13)

式中，c為聲速。流體在界面右側(cè)，故取左特征線方程

dp-ρcdu=0

(14)

式(11)、式(12)分別向后和向前差分

(15)

式中：下標(biāo)“I”為界面處的參數(shù)；上標(biāo)“n”，“n+1”為時(shí)間步。

在流固界面處：當(dāng)固體處于受壓狀態(tài)，界面受力方向從流體指向固體，pI=-σI；當(dāng)固體處于受拉狀態(tài)，界面受力方向從固體指向流體，pI=σI。

水的密度可由等熵狀態(tài)方程確定

(16)

式中：N為水的絕熱指數(shù)；ρ0=1.0×103kg/m3；A=1.0×103Pa；B=3.31×108Pa。

在流固界面變形較小的情況下，求解固體一側(cè)的網(wǎng)格坐標(biāo)

(17)

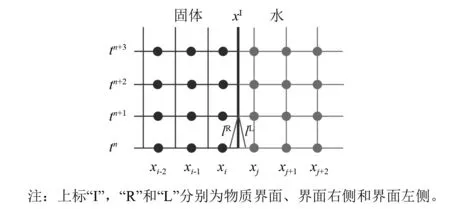
圖1 特征線法求解黎曼問題

1.4 MGFM賦值法則

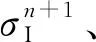
(18)

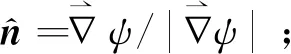
(19)

式中，dis為點(diǎn)與面之間的最短距離。

圖2 MGFM賦值法則

在數(shù)值模擬中，由于界面的移動(dòng)，流體虛擬節(jié)點(diǎn)有時(shí)候會(huì)轉(zhuǎn)變?yōu)檎鎸?shí)節(jié)點(diǎn)。根據(jù)等熵修正思想，為避免數(shù)值振蕩，用相鄰真實(shí)節(jié)點(diǎn)的狀態(tài)代替虛擬節(jié)點(diǎn)的狀態(tài)(見圖3)。

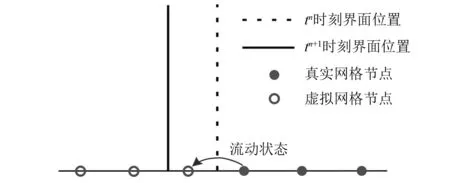
圖3 賦值修正步

1.5 數(shù)值模擬步驟

選取無量綱參考態(tài)：壓力pref=0.1 MPa,密度ρref=1.0×103kg / m3，長度lref=1.0 m，速度uref=10 m/s，時(shí)間tref=0.1 s。用Zwas格式[15]離散固體控制方程；用五階WENO格式[16]離散流體控制方程；用三階Runge-Kutta方法離散時(shí)間項(xiàng)。使用歐拉網(wǎng)格離散流體區(qū)域，并求解網(wǎng)格節(jié)點(diǎn)的狀態(tài)值；使用歐拉網(wǎng)格求解固體區(qū)域并求解網(wǎng)格中心的值。數(shù)值模擬步驟如下：

步驟1用近似黎曼解算器成對(duì)求解界面兩側(cè)的流體網(wǎng)格節(jié)點(diǎn)和固體網(wǎng)格中心的狀態(tài)；

步驟2用1.4節(jié)中的賦值法則對(duì)虛擬區(qū)域賦值；

步驟3用當(dāng)前時(shí)刻的狀態(tài)值求解下一時(shí)刻流體網(wǎng)格節(jié)點(diǎn)(包括虛擬節(jié)點(diǎn))和固體網(wǎng)格中心(包括虛擬網(wǎng)格中心)的值；

步驟4用式(17)求解界面位置，并根據(jù)新界面重新劃分真實(shí)區(qū)域和虛擬區(qū)域；

步驟5回到步驟1進(jìn)行一下時(shí)間步的求解。

2 數(shù)值測試

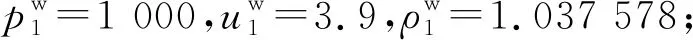
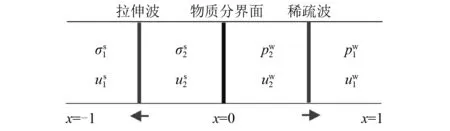
圖4 固體側(cè)的拉伸波與流體側(cè)的稀疏波示意圖

將計(jì)算域劃分為400個(gè)網(wǎng)格，網(wǎng)格步長Δx=0.005。水的絕熱指數(shù)N=7.15；固體密度ρ=7.8、彈性模量E=2.06×106、泊松比ν=0.25。圖5表明數(shù)值結(jié)果和理論結(jié)果吻合很好且沒有數(shù)值振蕩。其中，理論結(jié)果的求解可參考文獻(xiàn)[17]。稀疏波的理論解在左右兩端各有一個(gè)折點(diǎn)；而稀疏波的數(shù)值解，由于數(shù)值誤差，兩端折點(diǎn)不明顯。表1給出了固體區(qū)域和流體區(qū)域的數(shù)值誤差，本文給出的賦值法則具有一階收斂精度。

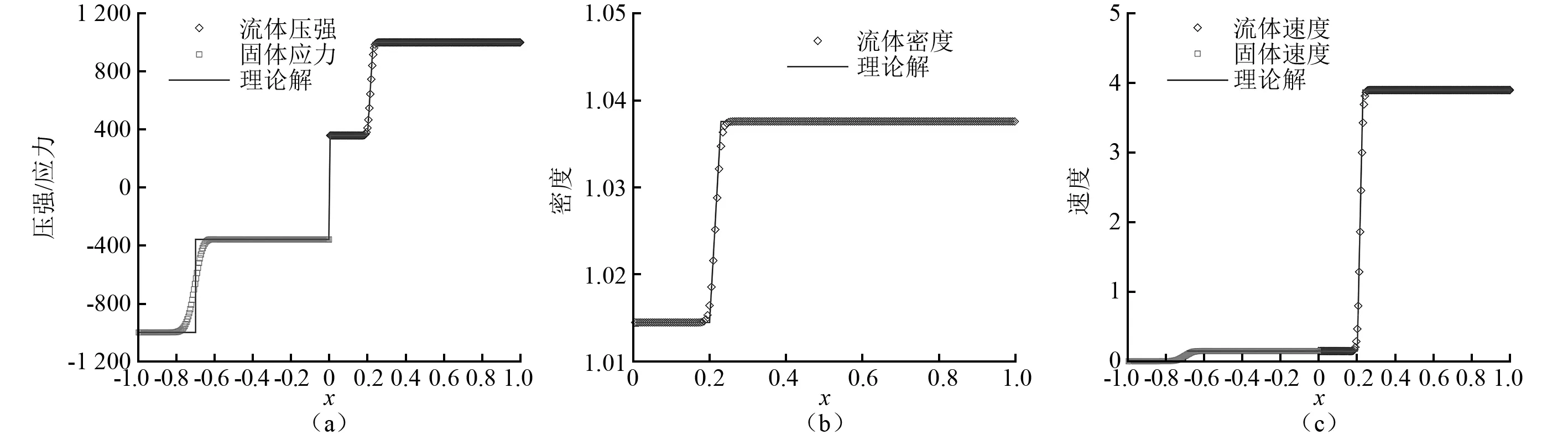
圖5 拉伸波與稀疏波的數(shù)值結(jié)果(t=1.243 429×10-3)

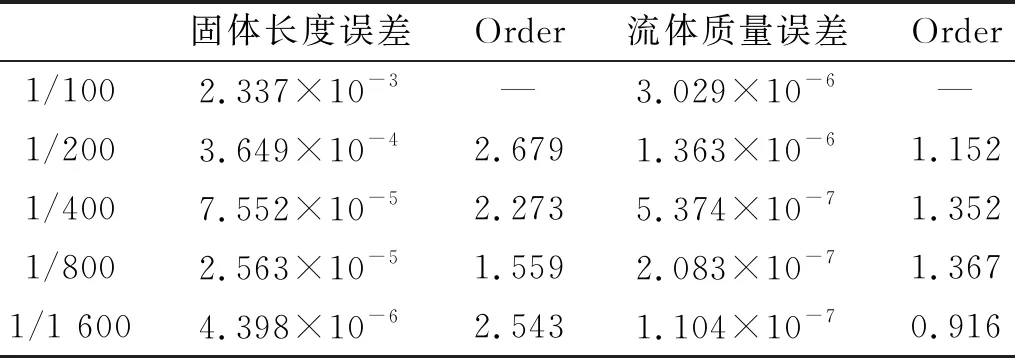
表1 數(shù)值測試結(jié)果

3 一維數(shù)值模擬

水艙殼體中的應(yīng)力波一般由水或者空氣中的壓縮波透射產(chǎn)生,如圖6所示。壓縮波透射產(chǎn)生固體應(yīng)力波后，才能進(jìn)一步在艙內(nèi)產(chǎn)生另一道透射壓縮波。本節(jié)分別對(duì)水和空氣中的壓縮波穿透問題數(shù)值驗(yàn)證。以下計(jì)算中，取網(wǎng)格步長Δx=0.005；空氣絕熱指數(shù)γ=1.38；水的絕熱指數(shù)N=7.15；固體密度ρ=7.8、彈性模量E=2.06×106、泊松比ν=0.25。

3.1 空氣中的壓縮波穿透水艙

圖6 空氣/水中的壓縮波穿透水艙

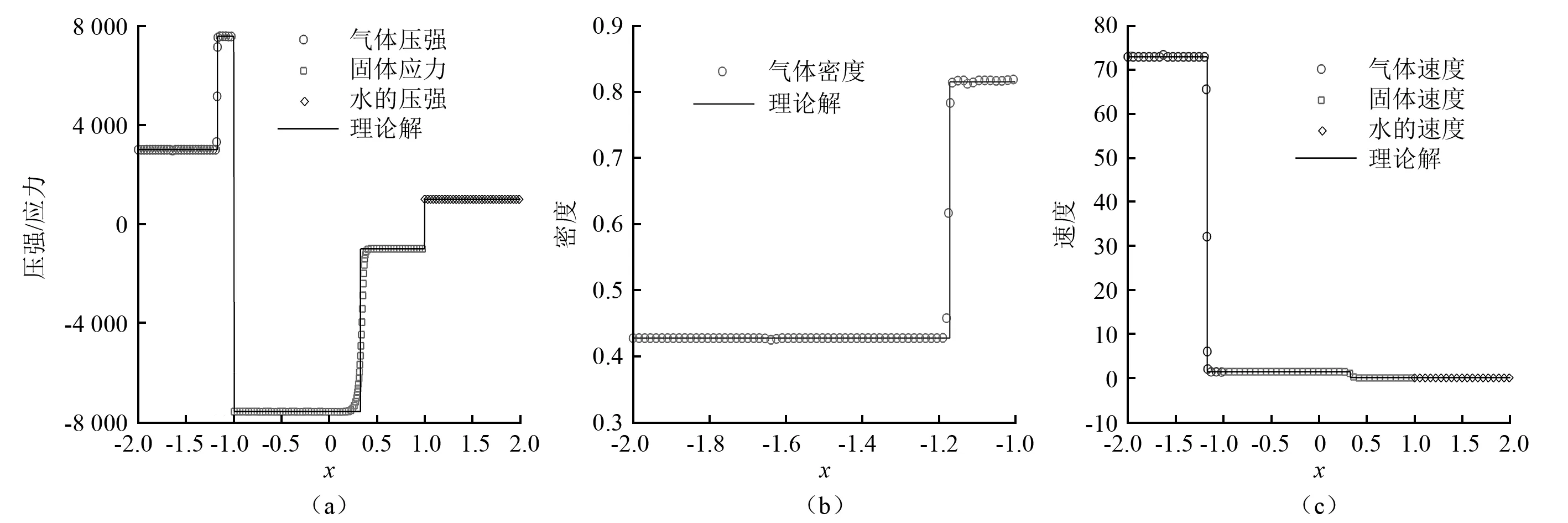
圖7 空氣中的壓縮波進(jìn)入水艙殼體生成固體應(yīng)力波(t=5.892 452×10-3)

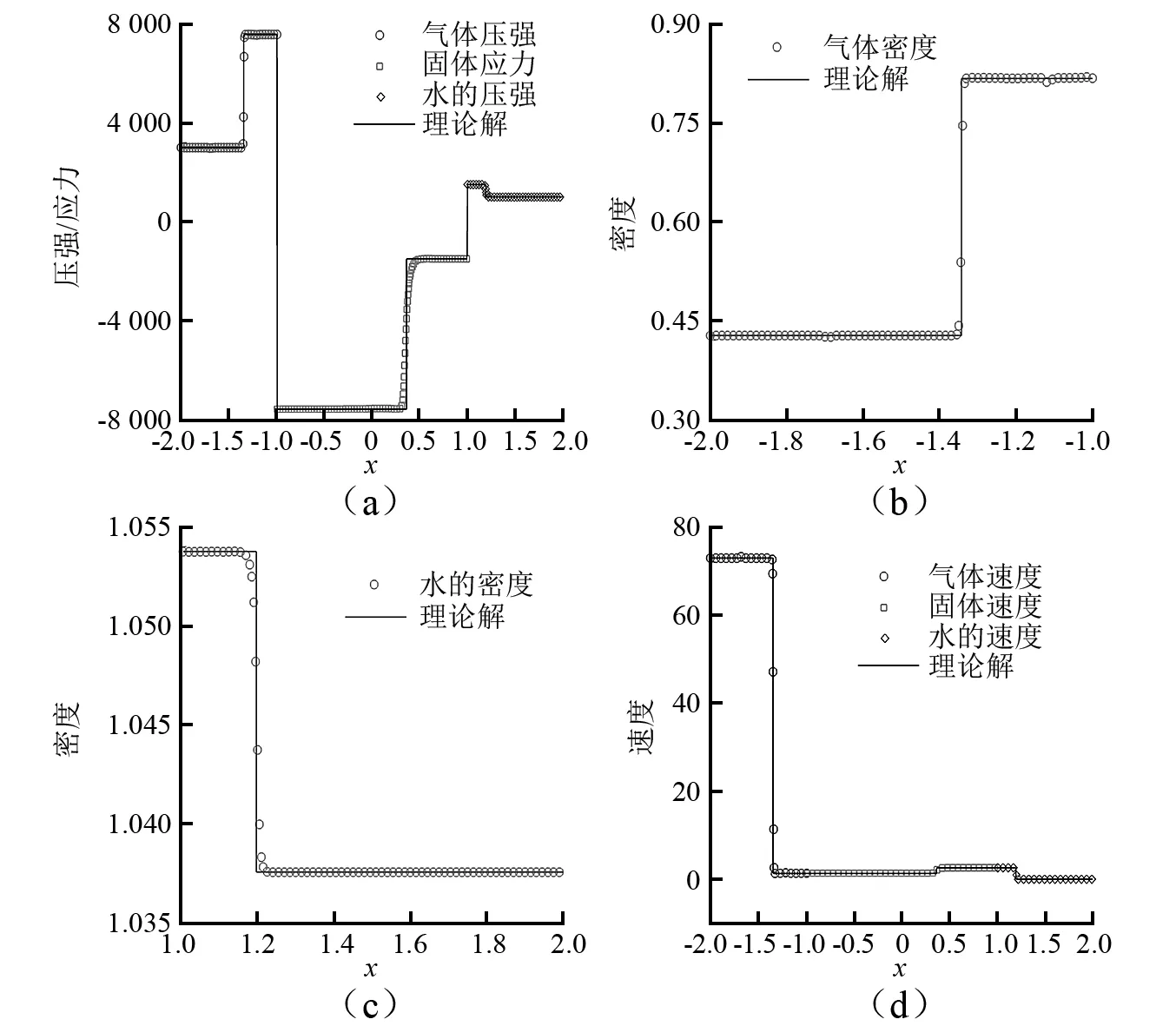
圖8 固體應(yīng)力波進(jìn)入水艙生成水中壓縮波(3.1節(jié))(t=8.081 076×10-3)

3.2 水中壓縮波穿透水艙

3.1節(jié)與3.2節(jié)中的數(shù)值結(jié)果均與理論解吻合一致。雖然虛擬介質(zhì)方法中的流固界面在數(shù)值模擬時(shí)是連續(xù)的，但是在數(shù)學(xué)上仍然是間斷的。這使得在數(shù)值模擬時(shí)，流體與固體必須分開求解，從而導(dǎo)致數(shù)值結(jié)果與理論解在局部區(qū)域有一些較小的差異。但是，這些誤差是收斂的，并沒有隨著計(jì)算的進(jìn)行而逐漸增長。

圖9 水中的壓縮波進(jìn)入水艙殼體生成固體應(yīng)力波(t=4.208 894×10-3)

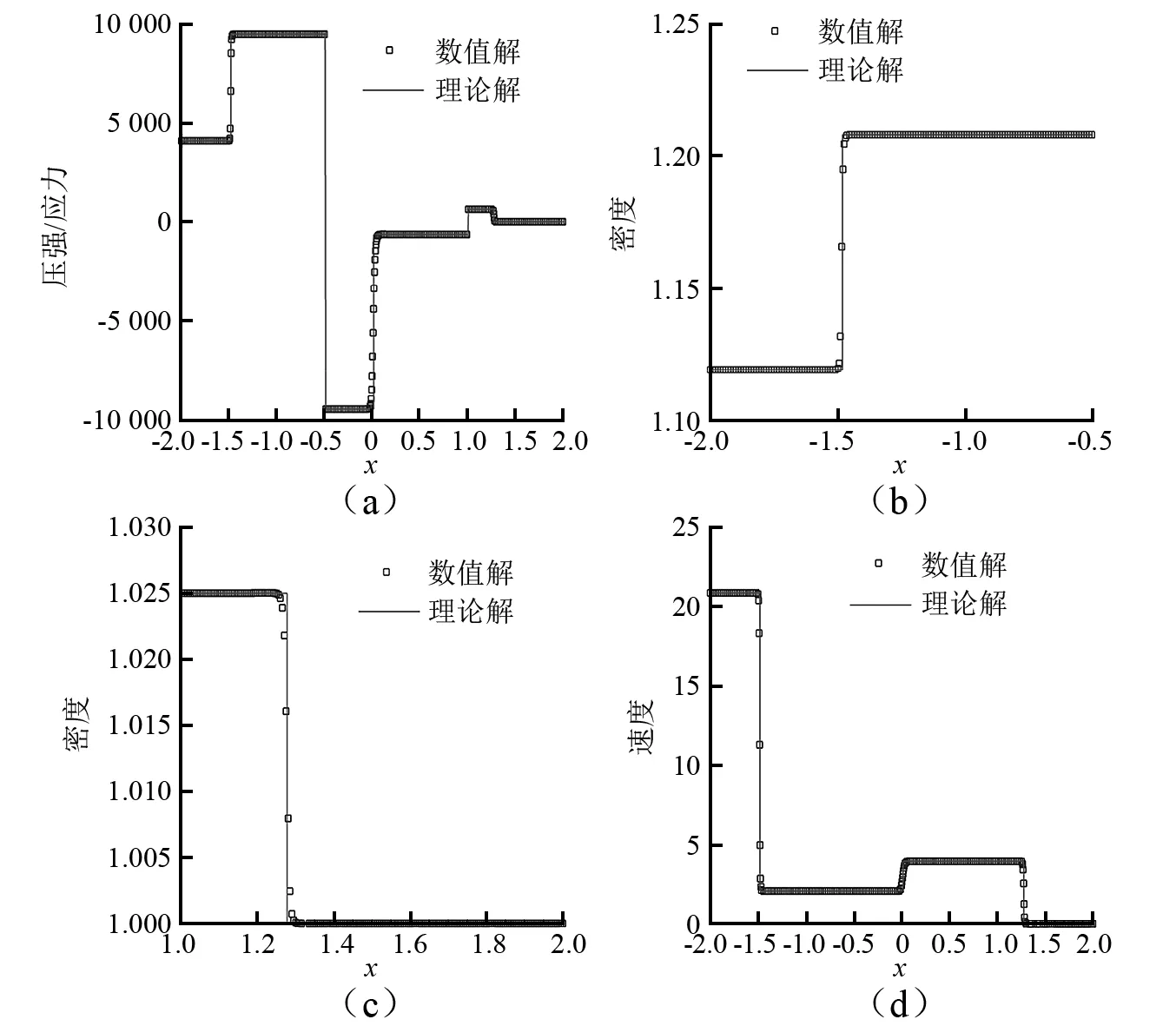
圖10 固體應(yīng)力波進(jìn)入水艙生成水中壓縮波(3.2節(jié))(t=6.734 230×10-3)

4 二維軸對(duì)稱數(shù)值模擬

圖11給出了一個(gè)水艙中心計(jì)算域的示意圖。計(jì)算域底面半徑0.5，高度1.0，殼板背面壓力分別取pw=100 kPa,200 kPa,400 kPa,800 kPa，取該中心區(qū)域的中軸面(虛線區(qū)域)建立二維軸對(duì)稱坐標(biāo)系，網(wǎng)格步長為Δx=Δy=0.005。水的絕熱指數(shù)N=7.15。殼板無量綱參數(shù)為：密度ρ=7.85、彈性模量E=2.06×106、泊松比ν=0.28、屈服強(qiáng)度4 000、抗拉強(qiáng)度4 800。

在底面中心A點(diǎn)按圖12加載應(yīng)力，加載范圍為直徑0.01的圓形區(qū)域。圖13(a)描繪了應(yīng)力波在水艙殼體內(nèi)部的傳播。如圖13(b)所示，在t=1.122×10-3時(shí)，應(yīng)力波波陣面已經(jīng)到達(dá)水艙殼體背面。圖14(a)、圖14(b)分別給出了由虛擬介質(zhì)方法和ALE方法得到的背面中心B點(diǎn)的動(dòng)態(tài)響應(yīng)。由于數(shù)值耗散，背面中心B點(diǎn)的應(yīng)力大約在t=7.0×10-4時(shí)開始增加。但波陣面大約于t=1.0×10-3時(shí)，到達(dá)背面中心，此時(shí)，應(yīng)力顯著增加。ALE算法在流固界面處采用弱耦合形式，只使用迎風(fēng)面(殼體側(cè))的狀態(tài)參數(shù)，界面應(yīng)力在峰值之前上升略早，峰值時(shí)間略晚；虛擬介質(zhì)方法在流固界面處采用強(qiáng)耦合形式，即同時(shí)使用界面兩側(cè)的狀態(tài)參數(shù)，界面應(yīng)力在峰值之前上升略晚，峰值時(shí)間略早。兩種方法得到的數(shù)值結(jié)果差異較小，應(yīng)力變化趨勢相近。表2表明，當(dāng)水艙內(nèi)的環(huán)境壓力增加后，應(yīng)力峰值也相應(yīng)的增加，峰值時(shí)間近似保持不變；同時(shí)也驗(yàn)證了虛擬介質(zhì)方法與ALE方法所得到的應(yīng)力峰值和峰值時(shí)間相近。圖15表明水艙壓力越大，透射波強(qiáng)度越大；同時(shí)，由于4個(gè)算例(pw=100 kPa,200 kPa,400 kPa,800 kPa)均使用相同的應(yīng)力加載，殼體背面的應(yīng)力波折射規(guī)律相近。

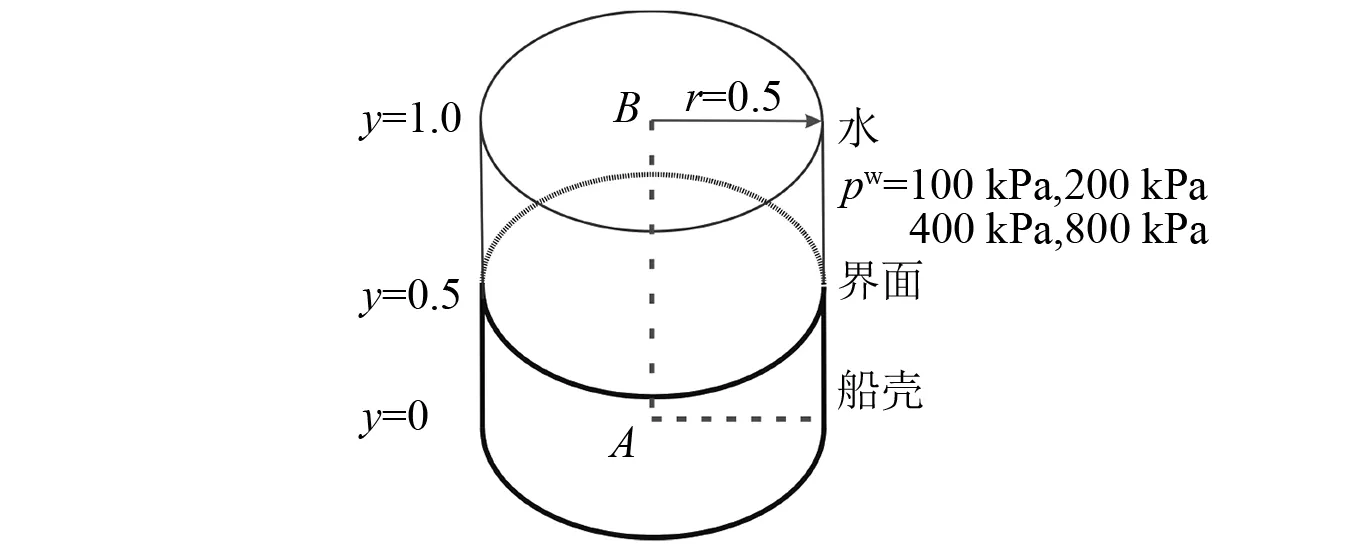
圖11 水艙中心計(jì)算域示意圖

圖12 應(yīng)力加載曲線

圖13 固體中的應(yīng)力波傳播(固體壓強(qiáng)ps=∑|σi|/3)

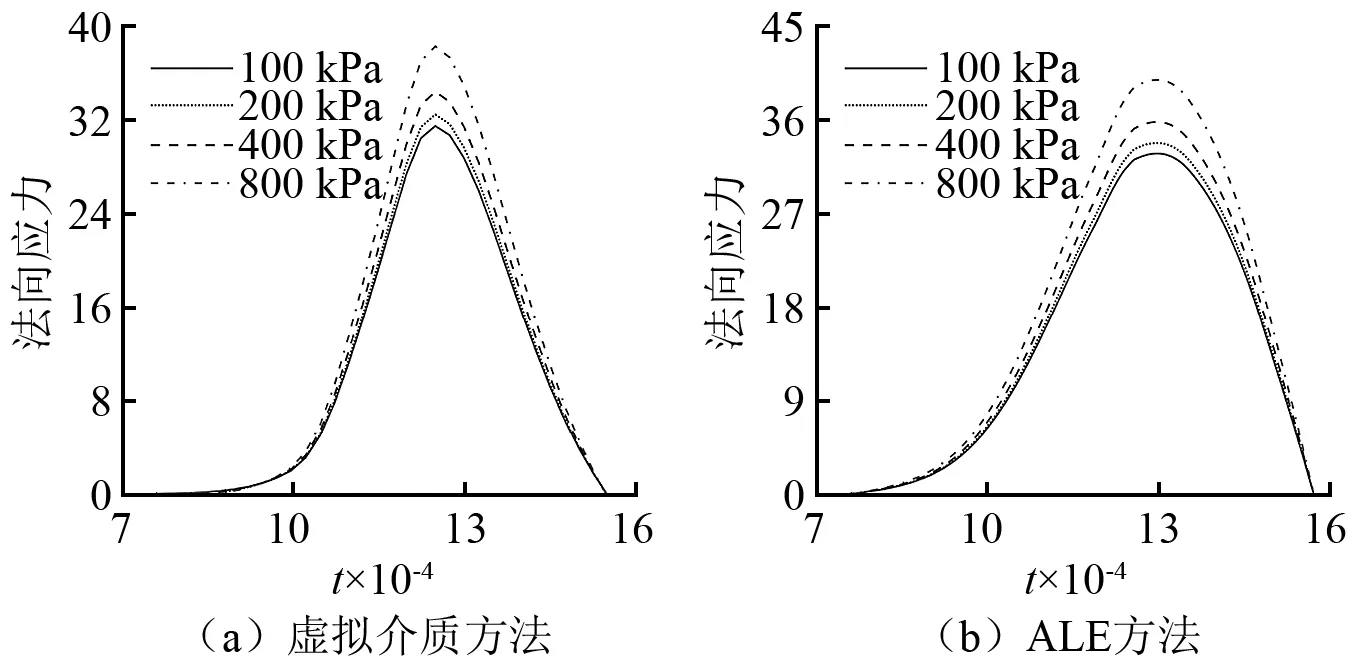
圖14 水艙殼體背面動(dòng)態(tài)響應(yīng)

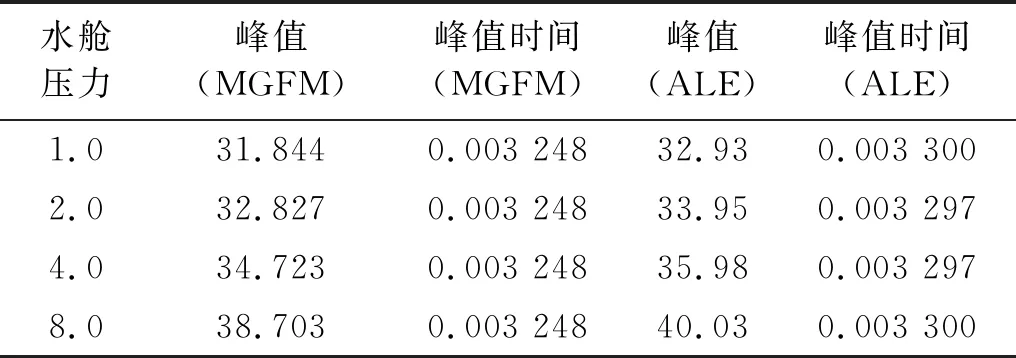
表2 峰值數(shù)值結(jié)果

圖15 應(yīng)力波在殼板背面的折射 (t=2.486×10-3，固體壓強(qiáng)ps=∑|σi|/3)

5 結(jié) 論

本文將虛擬介質(zhì)方法應(yīng)用到應(yīng)力波在流固界面處的折射問題，并給出了對(duì)應(yīng)的計(jì)算法則；數(shù)值測試表明，提出的計(jì)算法則具有一階精度。本文對(duì)水艙殼體中的應(yīng)力波穿透水艙的過程進(jìn)行了數(shù)值模擬和理論分析，一維數(shù)值結(jié)果與理論解能很好地吻合。多維數(shù)值模擬驗(yàn)證了虛擬介質(zhì)方法與ALE方法得到數(shù)值結(jié)果相近。對(duì)應(yīng)力波穿透水艙的初步研究表明，水艙加壓后，透射波的強(qiáng)度也相應(yīng)地增加；在不改變初始應(yīng)力加載的情況下，應(yīng)力波在水艙殼體背面的折射規(guī)律也對(duì)應(yīng)的近似不變。