珩磨加工中運動仿真分析與工藝實踐

閔浩晨，寧會峰，2，龔 俊，2，師志鵬

（1.蘭州理工大學機電工程學院，甘肅 蘭州 730050；2.蘭州理工大學數字制造技術與應用省部共建教育部重點實驗室，甘肅 蘭州 730050）

1 引言

珩磨是磨削加工的一種特殊形式，已成為發動機汽缸、工程機械液壓缸與精密聯軸器加工不可或缺的工藝技術。珩磨是缸孔的最終精密加工步驟，形成缸孔的結構形狀、尺寸和表面精度，對缸孔的性能與壽命起到決定性作用。因此，研究缸孔珩磨的運動參數是十分重要的，在珩磨過程中，每條油石都均勻的固定在珩磨頭上，珩磨頭的運動直接影響缸孔珩磨的質量。所以這里著重對珩磨的運動、軌跡形成及加工過程進行分析，深入研究不同參數的選擇對于珩磨加工質量的影響，從而選出最優的參數方案。

文獻[1]建立了珩磨軌跡分布與珩磨去除量的轉換關系，對珩磨軌跡進行了優化，提高了缸孔的形狀精度；文獻[2]使用MATLAB軟件模擬和分析了發動機氣缸鏜孔過程中油石磨粒的軌跡，通過研究發現，磨粒分布存在缺陷，提出了改善氣缸缸孔形狀的幾種措施；文獻[3]以圓柱形珩磨頭為研究對象，對珩磨頭進行運動和動力學分析，探討了珩磨頭的設計與仿真；文獻[4]建立了四種常用圓柱度誤差評定方法的數學模型，并將收斂因子的粒子群優化算法應用于圓柱度誤差的目標函數優化問題，比較了各種模型的計算精度；文獻[5]以單體泵的柱塞孔為研究對象，構建了珩磨加工的有限元模型，對仿真分析做了比較、優選工藝參數。綜合以上研究現狀，珩磨的參數分析現在還處于摸索階段，雖然理論研究和仿真分析做得比較充分，但是其并沒有與實驗相結合起來，能進行實驗驗證說明的研究現在還比較少。針對這一問題，首先對珩磨的三維軌跡進行重構，分析影響到珩磨軌跡的運動參數；其次選擇參數建立加工方案，在仿真分析之后得出數據，對所得數據進行圓柱度誤差評定。其中，圓柱度是評判缸孔加工質量的一個重要因素，如果圓柱度不在基本范圍之內，缸孔形狀會產生腰鼓形、馬鞍形、錐形和桶形等不滿足基本使用條件的廢品，帶來效率下降、壽命減短等問題。最后得到正確的圓柱度數據，對比缸孔之間質量水平不同，選擇出最優的缸孔加工方案，并進行實驗驗證，實現珩磨加工運動參數對珩磨質量影響的綜合性分析。

2 珩磨軌跡形成過程的分析

2.1 運動參數的選擇

在珩磨的實際加工中，珩磨頭旋轉并往復運動，往復運動包括三個工作段：下行程、下端滯留和上行程。根據珩磨加工情況，選取實際加工的參數：在珩磨頭上均勻分布著八條油石，珩磨頭往復速度V、旋轉速度n=230r/min、油石長度為l=60mm、缸孔高度L=150mm、兩端越程量為l1=l2=20mm、下端停留時間t3=0.3s，油石上每隔15mm 取一磨粒點，這樣沿油石的長度方向均勻的取4個點，可以直觀的反映出磨粒軌跡的分布。

圖1 珩磨加工示意圖Fig.1 Honing Process Diagram

2.2 珩磨中油石三維軌跡的重構

當珩磨頭的旋轉速度、兩端越程量和下端停留時間恒定，往復速度改變時，珩磨頭的旋轉相位角將相應地改變。珩磨頭旋轉的相位角角度，在改變往復速度的情況下，可以通過計算得到。珩磨頭的行程距離Lx=L+l1+l2-l=130mm，油石下行程時間為t1=Lx/V；則油石上行程的時間為t2=t1=Lx/V，t=t1+t2+t3=（15.6/V）+0.3。珩磨頭在一個周期內所轉動的角度：θ=nt=n/60×（15.6/V+0.3）×360°=（15.6/V+0.3）×1380°。此時，在往復周期內選擇合適旋轉相位角，V=15.6×［（θ/1380-0.3）］。當V=15.6×［（9t-41.4）/138］，θ=πt/4（t為正整數），取t=28、26 時的運動軌跡圖，當t=28 時，V=23.807m/min；t=36時，V=31.946m/min。根據以上參數進行計算，使用MATLAB 模擬出珩磨的三維軌跡圖。

圖2 往復速度為23.807m/min 時的三維軌跡Fig.2 3D Trajectory Reciprocat’s Speed at 23.807m/min

圖3 往復速度為31.946 m/min 時的三維軌跡Fig.3 3D Trajectory Reciprocat’s Speed at 31.946m/min

在珩磨過程中，珩磨頭的運動是旋轉運動和上下運動的綜合運動，因此油石的軌跡是交叉分布的，這樣才形成了交叉網紋。而油石的旋轉速度和往復速度決定了網紋的分布情況，在圖2 與圖3 中可以大致看出，在不同往復速度下，油石運動軌跡也產生了變化，珩磨頭的往復速度影響到了缸孔珩磨的效果。

2.3 運動參數對珩磨軌跡的影響

現在將上述油石的三維分布軌跡轉化成為二維圖形，這樣就能夠更加直觀的觀察油石軌跡分布情況，如圖4、圖5 所示。對油石軌跡的分布差異直接進行對比。

圖4 往復速度為23.807m/min 時的二維軌跡Fig.4 2D Trajectory Reciprocat’s Speed at 23.807m/min

圖5 往復速度為31.946m/min 時的二維軌跡Fig.5 2D Trajectory Reciprocat’s Speed at 31.946m/min

由上面的二維平面軌跡圖分析可知，油石軌跡沿缸孔深度方向分布不均勻，而珩磨頭的往復速度很大程度上影響到了磨粒的空間分布情況。圖4 中的運動軌跡具有較小的重合度，網紋的分布比較相對均勻，所以缸孔內表面珩磨很充分，保證了缸孔的表面精度；而圖5 中的油石運動軌跡重合度較高，這會導致缸孔的部分表面被重復加工，整體內表面加工不均勻，極大地影響到了缸孔的表面精度。通過上述表象分析，推斷出了運動參數直接影響缸孔性能參數，但缸孔的性能參數影響值差異無法確定，針對存在的問題，通過對珩磨過程進行仿真分析，研究運動參數對于珩磨性能參數的影響。

3 珩磨加工的仿真分析

3.1 珩磨加工的仿真機理

珩磨加工過程中，在缸孔內壁發生微小的塑性應變，這種塑性應變等效交叉網紋的作用變量，這些變量的作用匯集在一起使得缸孔發生變形。珩磨仿真運算結束后，將會得到缸孔的應變云圖，這時對缸體的變量數據進行采集、匯總，對集合起來的變量數據進行計算并分析出缸孔的圓柱度，對圓柱度誤差進行評價。

3.2 建立三維模型

首先，建立珩磨頭的三維模型，如圖6 所示。建立模型時，要使用柱坐標系，將珩磨頭結構盡量簡化，在保證了基本結構的前提下，盡可能的提高運算速度。在仿真分析下，珩磨頭與油石均不考慮其本身的磨損與變形，即珩磨頭與油石是剛性實體，這樣在一定程度上減少了多余運算量。

圖6 珩磨頭與缸孔的有限元模型Fig.6 Finite Element Model of Honing Head and Cylinder Hole

珩磨加工過程中，因為加工余量很小，所以僅需保留被加工材料的部分來制定缸孔的有限元模型，考慮到溫度、應力和塑形變形的影響，采用Johnson-Cook 模型構建缸孔材料，實現磨削過程中切屑分離，在軸向方向細化了網格，能更加完整、精確的運算出真實的工況，最后，裝配珩磨零件，獲得完整的有限元模型。

3.3 模型參數賦予

仿真油石與缸孔材料的參數與Johnson-Cook 本構常數如下：

表1 缸孔材料參數與Johnson-Cook 本構常數Tab.1 Cylinder Hole Material Parameters and Johnson-Cook Constitutive Constants

珩磨在加工過程中有著加工速度快、精度高等特點，經過珩磨三維軌跡構成運動參數的分析：首先，珩磨頭的往復速度是影響珩磨質量的一個重要因素；其次，珩磨過程的珩磨余量和下端滯留時間也會影響到缸孔材料的剝離程度。因此，針對這三個方面制定不同的工藝方案進行仿真，驗證在哪一種方案下珩磨加工精度能達到最高，通過理論、仿真方法來驗證假設是否成立，如表2 所示。

表2 制定的工藝方案Tab.2 The Processing Plan

在得到了仿真應變云圖之后，對模擬運算加工后的缸孔坐標數據進行采集，如圖7 所示。其中，方案1 的缸孔坐標數據，如表3 所示。

圖7 仿真應變云圖Fig.7 The Simulation of Strain Nephogram

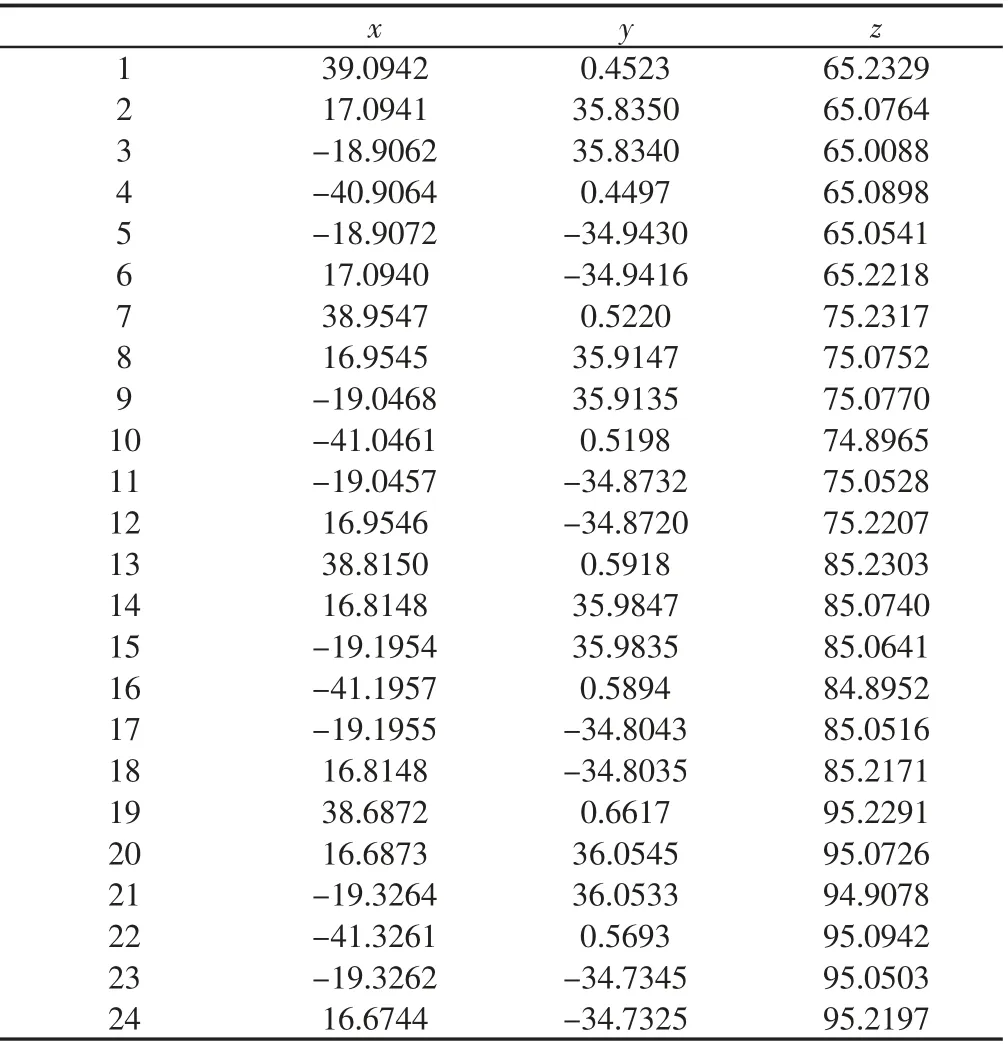
表3 缸孔變量數據Tab.3 Cylinder Hole Variable Data

4 仿真數據的后處理

4.1 圓柱度誤差評價的數學建模

圓柱度誤差指的是理想圓柱面與實際被測圓柱面之間的變動量，確定理想圓柱面的位置是誤差評定的第一要素，理想圓柱面的選擇應滿足最小條件，即被測實際數據相對于理想數據的最大變動量為最小值。根據理想圓柱面的位置不同，分為最小區域法、最小二乘法、最小外接圓柱法和最大內接圓柱法，其中最小區域法是最為有效，計算結果最佳的結論[4]。

首先，建立空間直角坐標系，如圖8 所示。設圓柱面的回轉軸線為L，位置由參數a、b控制，方向由u、q控制，可推導出方程：

圖8 被測圓柱面及理想軸線Fig.8 The Measured Cylinder Surface and Ideal Axis

最小區域法評價圓柱度誤差的定義如下：被測對象由兩個同軸的理想圓柱面包含其中，兩個圓柱面的半徑差為最小值時，它們之間包含的區域就是最小區域，半徑差即為圓柱度誤差。根據最小區域法定義，得出圓柱度誤差目標優化函數為：

4.2 圓柱度誤差的數學運算

而將方案一至四的缸孔坐標數據均采集并逐步迭代運算，得到的結果，如表4 所示。

表4 仿真計算的圓柱度Tab.4 The Simulation Calculation of Cylindricity

可以看出，方案1 與2 的進給余量與下端滯留時間相同、往復速度不同的情況下，所得到圓柱度的數值明顯相差，表明珩磨過程的往復速度對缸孔精度有一定的影響。方案1 與3 的往復速度與下端滯留時間相同、進給余量不同的情況下所得到圓柱度的數值最小，進給余量對于缸孔精度的影響并不明顯。方案2 與4的往復速度與進給余量相同、下端滯留時間不同的情況下，發現下端滯留時間對于缸孔精度的影響不大。

5 珩磨的加工實驗

5.1 珩磨的實驗設備

前面進行了珩磨三維軌跡、加工模擬、仿真分析，雖然計算已經得出滿足要求的圓柱度數據，但是沒有經過試驗驗證，理論分析依然具有一定的局限性。我們將計算參數運用于實踐加工，利用仿真數據開展實驗。前面建立的珩磨磨削加工模型是從三維軌跡的成型機理出發，依據理想工況做出假設而得到的，需要試驗驗證其是否對實際加工具有指導意義。

實驗設備為銀川大河2MK2210 型數控珩磨機床，機床配備的珩磨頭可加工的工件為內孔直徑為Φ80mm～Φ100mm 的工件。機床自身量儀可以實現在線測量并可以實現自動加工。

圖9 銀川大河2MK2210 型數控珩磨機床Fig.9 Yinchuandahe’s 2MK2210 NC Honing Machine Tools

為了驗證珩磨加工測量精度，能夠快速的測量出精度數據，專門配備了PULCOMV4 量儀。PULCOM V4 電動測量儀連接機床系統進行有效測量，實現對工件的在線實時測量和加工后的手動測量。該氣動量儀最小分辨尺寸為0.1μm，數值顯示可以根據倍率變換進行自動調整，可顯示最大范圍為（±999.9）μm，且表頭可根據量程的切換顯示（±10～±50）μm、（±100～±500）μm 的測量范圍。

5.2 加工實驗結果分析

圖10 實際加工圖Fig.10 The Actual Processing Figure

珩磨加工后的實驗工件，從左往右分別是按方案一至方案四順序排列，在工件內部可以看到清晰的加工珩磨網紋，每個加工工件內表面光潔度均有不同，表面質量明顯存在差異，并存不同規律的珩磨網紋，如圖10 所示。通過觀察發現方案1、3 的珩磨網紋平整、連接性平滑，方案2、4 的珩磨網紋與方案1、3 有明顯的差距、連接性也有所降低，這表明運動參數的選擇直接影響珩磨的精度。使用珩磨機床上的氣動測量儀（PULCOM V4 量儀）對工件進行測量，測得的結果，如表5 所示。

表5 實驗加工的圓柱度Tab.5 The Experiment Process of Cylindricity

將所有方案結果統計繪制出圓柱度對比圖，如圖11 所示。利用仿真數據與實驗結果進行整理和對比分析，實驗測量精度與仿真計算數據非常接近，兩條折線的相似度也非常高，通過使用仿真參數加工缸孔，可以有效的控制缸孔的圓柱度精度，獲得較好的珩磨效果。

圖11 仿真計算與實驗加工的圓柱度對比Fig.11 The Simulation Calculation and Experimental Processing’s Cylindricity of Contrast

在理論和實驗的結合過程中，突出解決了三個關鍵問題：

（1）通過珩磨運動參數構建了珩磨加工三維軌跡，其中珩磨頭的運動參數是影響缸孔軌跡的主要因素，重點分析在不同參數下形成的不同的運動軌跡，從而得到了珩磨幾何軌跡、疏密分布程度和缸孔圓柱度之間的關系，初步建立仿真分析方法。（2）珩磨仿真運用實際加工中，現在在國內仍處于空白階段，相關理論研究內容較少，這里通過運動參數的選擇、三維軌跡的重構、珩磨加工的仿真創建模型、圓柱度誤差評價的數學建模、設置接觸以及設立邊界條件等一系列理論流程實施后，構建了珩磨加工的仿真系統，能夠模擬珩磨加工并運算出在理想條件下缸孔加工的應變云圖。（3）圓柱度誤差的評價采用了最小區域法，得到了仿真應變云圖與形變云圖，通過采集仿真缸孔數據計算出圓柱度，在與實驗測得的圓柱度進行對比，驗證運動參數對于加工質量產生影響。這種參數優化的思路與實驗過程相結合的方法，將為今后的制造和設計提供有力的理論指導。

6 結論

圍繞珩磨過程中運動參數選取，運用三維軌跡和有限元模型分析，在不同參數下對缸孔圓柱度影響進行分析，得到了珩磨過程中往復速度對缸孔圓柱度的影響效果；通過理論仿真結果與實驗研究數據對比和分析，證明運用優選方法可以準確確定珩磨過程中運動參數，得到最佳的珩磨缸孔圓柱度，達到保證加工精度的目的。