學生視角：讓數學學習接地氣

王淑芳

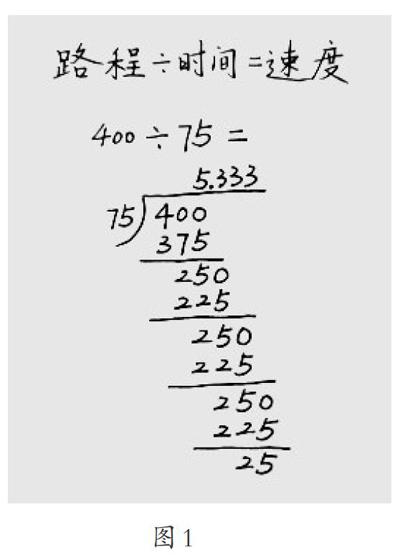
學生視角，即教師俯下身子從學生的認知視角出發，順著學生的認知思路展開教學，讓學生較好地理解數學知識的本質，促進其學習力和數學核心素養的提升。學生視角不僅是一種教學觀念，更是一種教學方式。學生視角不是一蹴而就的，需要一系列復雜的思考和實踐過程才能找到門道。筆者以人教版小學數學教材五年級上冊“循環小數”教學為例，闡述學生視角的內涵及踐行所需要的階段和相應環節。

一、解讀教材，厘清本質

踐行學生視角的前提是教師要深刻理解教學內容，認真解讀教材，厘清知識本質。在教學“循環小數”時，教師利用教材中的例7，首先以運動會場景圖為素材，讓學生迅速明白要求的是王鵬跑步的速度，馬上想到“路程÷時間=速度”，從而快速列出算式。接著以“400÷75”的豎式計算為樣本，讓學生發現計算過程的規律。教材呈現了三個規律：永遠除不完、商的小數部分重復出現3、余數25依次不斷重復出現。這三個規律哪一個最關鍵呢？筆者認為，余數25依次不斷重復出現，導致算式除不盡，也導致商的小數部分重復出現3，因此“余數25依次不斷重復出現”這一規律最關鍵，要特別關注。

教材中的例8安排了兩道算式，讓學生先計算，再說一說商的特點。筆者認為，第一道算式和例7類似，都是商的小數部分重復出現一個數字，可以省略。第二道算式的商重復出現兩個數字，是新的循環形式，應該重點關注。在學生有所體驗的基礎上，教師再揭示循環小數、循環節的概念以及循環小數書寫的簡便形式。

教師最后引導學生觀察“15÷16”和“1.5÷7”這兩道算式的商，讓學生直觀地認識什么是有限小數，什么是無限小數。循環小數當然是無限小數，但無限小數不一定是循環小數，教師可借助相應例子讓學生領會這種關系。

二、課前調查，把握學情

解讀教材可以厘清知識起點，但知識起點不一定是學生的實際起點。因此，要想讓學生視角落在實處，課前還是要通過一定的方式了解學生的實際起點。教師在班上做了一個小調查，調查問題如下。

1.大家聽說過循環小數嗎？（5個學生舉手）

2.你們認為循環小數是怎么樣的？（第一個學生：循環小數就是除不完的小數。第二個學生：循環小數就是有數字循環出現的小數。第三個學生：0.33333…就是循環小數。第四個學生：循環小數就是有一個數字循環出現的小數。第五個學生：我只是聽說，沒看到過。）

經過調查，筆者了解到全班近一半學生聽說過循環小數，也可能知道循環小數的一些特點，但這些“知道”都是碎片化的、不完整的。由此可見，教師不能完全照搬參考用書及參考資料上的做法，一定要在課前了解學生的真實起點，選擇適合本班學情的教學方法。

三、順應學生，層次推進

教師在教學時要努力順應學生，然后有層次、有節奏地推進，這是踐行學生視角的關鍵。筆者在解讀教材及學情調查的基礎上，決定以教材上的思路為主，適當做了一些調整，經歷了如下的教學過程。

（一）算用結合，列式計算

算用結合有助于將計算與問題解決融為一體，適合學生視角，是新教材編排的一大特色。筆者先出示教材中的例7主題圖，然后依次圍繞下面三個問題展開教學。

1.“平均每秒跑多少米”是求什么？

2.怎么求速度？

3.真的除不完嗎？

這一教學環節顯得干脆利落，在算用結合中把學生迅速引向列式計算，讓學生初步感受循環小數的特點。當學生紛紛表示除不完的時候，筆者順勢和學生一起在黑板上計算，展示計算過程（如圖1）。

（二）觀察算式，發現規律

呈現計算過程有利于學生發現規律。根據黑板上的算式，筆者依次圍繞下面四個問題展開教學。

1.觀察這個豎式，你發現了什么？

2.商的小數部分重復出現“3”的原因是什么？

3.算式除不完的原因是什么？

4.這三個規律，最關鍵的規律是哪一個？

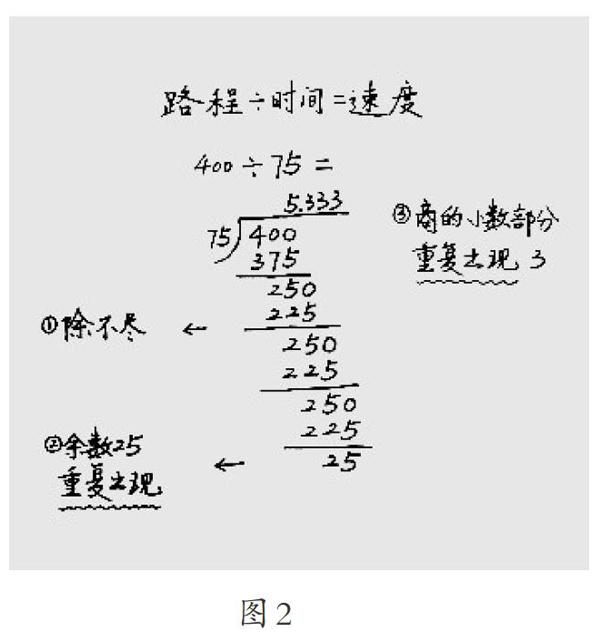
學生在回答第一個問題時，筆者根據學生回答情況適時在算式旁邊板書三個規律：永遠也除不完、余數25重復出現、商的小數部分重復出現3（如圖2）。

在拋出第二個問題后，學生不知不覺地把目光聚向余數，當余數25第一次出現時，商出現3;第二次出現時，商出現3;第三次出現時，商又出現3。于是學生紛紛明白：原來余數出現25，商的小數部分就出現3，因此商的小數部分重復出現3的原因是余數25重復出現。有了解決第二個問題的經驗，第三個問題就可以迎刃而解。

當解決了前三個問題后，第四個問題也就水到渠成，最關鍵的規律就是余數25重復出現。至此，學生自然就建立起這樣一個觀念：余數重復出現會造成商的小數部分重復出現某個數字;余數重復出現，除法豎式就除不完。

（三）認識名稱，體驗變化

學生的感性認識是建立數學概念的必要條件。在學習例7的基礎上，筆者順勢提出“5.3333…”就是循環小數，重復出現的3只要寫一個3，但要在它的上面點上一點，這個點就叫作循環點，表示重復出現。這個循環小數讀作：五點三，三循環。然后寫好單位，把題目做完整（如圖3）。

然后，筆者引導學生圍繞下面幾個問題展開教學。

1.結果是循環小數嗎？它的簡便形式怎么表示？

2.為什么商的小數部分會有兩個數字重復出現？

由于商的小數部分中的45重復出現，學生都知道這是循環小數。簡便形式就是商的小數部分重復出現的45只寫一個，并且在4和5上面點上循環點。

由于有了上一環節的知識，學生會知道因為余數5和6依次不斷交替重復出現，所以商的小數部分就會重復出現45。這樣一來，學生加深了對循環小數的認識。

（四）提煉特征，建構概念

在學生感性經驗積累到一定程度的時候，適度的提煉有利于學生更好地厘清概念本質。筆者在完成上一教學環節的基礎上，讓學生閱讀教材33～34頁的內容，然后圍繞下面三個問題展開教學。

1.這兩個循環小數共同的特征是什么？

2.什么叫依次不斷？什么叫循環節？

3.什么叫循環點？如何點？

在回答第一個問題后，筆者順勢板書：小數部分的一個數字或幾個數字依次不斷重復出現。

第二個問題，學生會根據板書回答：“依次不斷，就是按順序重復出現，不會停下。”學生也會明白小數部分重復出現的數字叫循環節，抓住教材中的“6.9258258…”這個循環小數，讓學生明白它的循環節是258，它是重復出現的，后面的省略號就表示依次不斷重復出現。

第三個問題，同樣抓住“6.9258258…”這個循環小數，它的循環節有三個數字，在此強調循環節有三個或三個以上的，只要在首和尾兩個數字上點循環點就可以，中間的數不用點循環點。

（五）定向訓練，鞏固新知

有針對性的定向訓練是鞏固新知的必要手段。本節課涉及知識點較多，考慮實際學情，筆者不想過多拓展，只圍繞核心知識點設計練習，有助于學生厘清知識要點。

1.判斷。

（1）一道除法算式，發現余數總是34，那么商肯定是一個循環小數。（）

（2）9.99999÷3的商是一個循環小數。（）

（3）兩個數相除，除不盡時，商是無限小數，而且是循環小數。（）

2.比大小。

0.123○0.12 0.9999999○0.9

2.268○2.267 0.1234○0.123

3.用簡便形式表示循環小數。

1.5555… ? ? ? ? ?1.7676… ? ? ? ? 1.2567567…

4.下面這個數的小數部分第99位是什么數字？小數部分前99位數字的和是多少？

0.234234…

第1題重在鞏固循環小數的本質特征、相關概念與無限小數的關系;第2題重在鞏固循環小數的特征;第3題重在鞏固循環小數的簡便記法;第4題重在鞏固學生對無限小數概念的理解，拓展學生的抽象思維。

總之，學生視角可以讓數學學習更接地氣。有了學生視角，我們就會考慮學生的學習起點、學習重點和難點、容易混淆的知識點、練習設計的針對性……由此可見，學生視角是促進學生學習力和數學核心素養提升的有效手段。

（作者單位：浙江省仙居縣田市鎮中心小學）