從習慣養成談數學學習中的“粗心”現象

黃洪毅

【摘要】本文主要從實際教學經驗出發，探討在數學學習中學生為什么容易出現“粗心”的現象，同時提出從習慣養成的角度幫助學生避免“粗心”，學會“細心”.

【關鍵詞】數學學習;粗心;養成習慣

筆者從事數學教學已有三十多年，每每考完數學做試題分析時，經常聽到學生抱怨，“這些題目我都會，就是粗心.”“我并不笨，只是沒上心.”比如-14結果算成了1，32=6，-1-2=-1，把“-”抄成了“+”，或者看漏了某個條件，更有8+9=16這樣的低級錯誤……

數學沒考好，真的是“粗心”所致嗎？不可否認許多家長也都認可這個觀點.但是筆者認為粗心是做錯題的結果，而不是原因.

誰都有粗心的時候，但在粗心表象下有很多更深層次的原因，如果沒有及時分析真正考不好的原因，一味以“粗心”為借口，長期下去，那數學學習可就徹底被所謂的“粗心”耽誤了.

1 學生“粗心”的原因

仔細分析這些錯誤，不難發現導致學生“粗心”的原因大致有以下幾個方面.

1.1 基本概念、法則等掌握不夠透徹

有些學生對課本里的概念、法則重視程度不夠，認為了解了就行，而不是去認真地理解掌握，因此在應用時就會出現各種“粗心”的現象.

例如在七年級學習“有理數運算”時，經常會有學生出現這樣的錯誤：（-5）2=-25，-14=1，32=6，…出現這些錯誤的主要原因就是對“冪”的意義理解不透，如（-5）2底數是-5，表示的是兩個-5相乘，所以結果應該是25，而不是-25;-14的底數是1，表示的是1的4次方的相反數，所以結果應該是-1，而不是1;32的底數是3，表示2個3相乘，所以結果應該是9，而不是6.在計算有理數加減時還有這樣的錯誤：-1-2=-1，錯誤的主要原因是對有理數減法法則理解不透，這里是減去2，所以應該是-1-2=-1+（-2），正確答案是-3，而不是-1.

1.2 解題時精神不集中

有些學生因為各種原因導致解題時經常一心二用，甚至一心三用：邊解題邊聽歌，或邊解題邊支起耳朵聽家里人的對話（或電視里的節目），或邊解題邊想著某件事……從而導致解題出現很多低級錯誤，大大降低了解題準確率.比如上面提到的8+9=16、把“-”抄成了“+”等低級錯誤.

筆者曾經遇到這樣一個學生，他在解一道一元一次方程題時是這樣做的：

原題：2（x-2）=4（1-x）.

他的解題過程：

2x-4=4x-4，

2x-4x=-4+4，

-2x=0，

x=0.

當我把他叫到面前，告訴他這題錯了，讓他自己找原因時，他找了半天才發現他把等號右邊括號里兩項的順序給弄反了.我讓他仔細回憶做題時的情況，他說他戴著耳機邊做題邊聽歌，做到這題時，因為左邊括號里是x-2，所以潛意識里右邊也就把x寫到了前面.

1.3 書寫潦草

有些學生不注意自己的書寫，尤其是在草稿紙上演算時更是龍飛鳳舞，東一筆，西一筆，導致抄錯數字、符號等現象發生.

例如，七年級學生在合并同類項時，有這樣一道題：3x+2y+2x-4y-2z.

有一個學生是這樣做的：

原式=（3x+2x）+（2y-4y）-2z

=5x-2y-22.

顯然，學生的答案是錯的，研究了半天，才發現他是因為書寫潦草，把最后一項-2z的字母z寫得有點像數字2，所以最后一項本應該是-2z，卻變成了-22.

類似這樣的錯誤，筆者不止一次碰到過.

1.4 閱讀理解能力有待提高

部分學生因為沒有養成良好的閱讀習慣，受碎片化閱讀的負面影響頗多，導致無法準確理解題意，經常出現漏掉題目中重要條件的情況.

2 為什么如此“粗心”

學生出現了“粗心”的錯誤時，在分析試題時可以進行這樣的反思.

2.1 “原本會做的，考試做錯了”——那就問問自己基本概念、基礎知識真的掌握了嗎？

例 若關于x的一元二次方程kx2-2x-1=0有兩個不相等的實數根，則k的取值范圍是（ ）.

A.k>1 B.k>-1

C.k>-1且k≠0D.k<1且k≠0

分析 根據一元二次方程的定義和Δ的意義得到k≠0且Δ>0，即（-2）2-4×k×（-1）>0，然后解不等式即可得到k的取值范圍.

解答 ∵關于x的一元二次方程kx2-2x-1=0有兩個不相等的實數根，

∴k≠0且Δ>0，

即（-2）2-4×k×（-1）>0，

解得k>-1且k≠0.

∴k的取值范圍為k>-1且k≠0.

選C.

點評 本題考查了一元二次方程ax2+bx+c=0（a≠0）的根的判別式Δ=b2-4ac：當Δ>0時，方程有兩個不相等的實數根;當Δ=0時，方程有兩個相等的實數根;當Δ<0時，方程沒有實數根.本題也考查了一元二次方程的定義.但因為沒有徹底理解一元二次方程的定義，二次項的系數不能為零，學生往往會選擇B，導致答案錯誤.

2.2 “簡單的，不該錯的，考試錯了”——那就問問自己做題時精力集中了嗎？平時解題的準確率高嗎？

例 36的算術平方根是（ ）.

A.6 B.-6 C.6 D.-6

分析 因為36=6，本題相當于考6的算術平方根是什么.答案是C.

點評 如果學生審題注意力不集中，就會選擇A.

2.3 “審題錯了，不是不會做”——那就問問自己閱讀習慣有沒有問題？平時解題時能否在題目中快速找出關鍵信息？

例 等腰三角形的一個內角是50°，則另外兩個角的度數分別是.

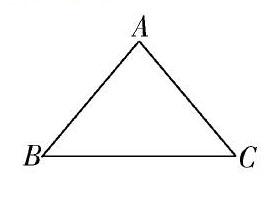
分析 如圖，根據等腰三角形的性質，推出∠B=∠C，則分為兩種情況：①當底角∠B=50°時，②當頂角∠A=50°時，再根據∠B=∠C和三角形的內角和定理求出即可.

解答 如圖，∵AB=AC，∴∠B=∠C.

當底角∠B=50°時，則∠C=50°，∠A=180°-∠B-∠C=80°.

當頂角∠A=50°時，

∵∠B+∠C+∠A=180°，∠B=∠C，

∴∠B=∠C=1[]2×（180°-∠A）=65°.

即其余兩角的度數是50°，80°或65°，65°.

點評 本題考查了等腰三角形的性質和三角形的內角和定理，應注意此題有兩種情況：①當底角∠B=50°時，②當頂角∠A=50°時.因此必須分類討論，針對各種可能一一作答才可以.可學生往往沒好好審題，沒有找準題目中的關鍵字“一個內角”“求另外兩個角的度數”，草率作答，當然會因為答案不完整而被扣分.

2.4 “我抄錯數字（符號）了，不該錯的”——那就問問自己書寫工整嗎？

不只要書寫工整，還要講究具體題目格式的規范性，計算過程中巧妙的書寫等，這些都影響著學生的計算正確率.

3 五大習慣避免“粗心”

那么，在數學學習中如何避免“粗心”呢？這里給大家介紹五個習慣方法，如果能在平時的學習、做題、作業中養成這些習慣，那么改掉“粗心”的毛病也就不在話下了.

3.1 養成仔細閱讀的習慣

學生拿到題目后讀題速度要慢，尤其是題目較長時，更要慢讀，細細讀，并且一邊讀，一邊思考，同時把重要的信息記錄下來，比如把已知的數據標示在題目圖上，題目沒有讀完不能妄下結論.

這樣一遍讀下來，有用的信息都正確進入自己的腦海，做題時就能正確運用所有條件，看錯題目、看漏條件這些現象就基本不會出現了.

3.2 養成工整書寫的習慣

有些復雜的數學題目需要根據已知條件列出很多方程、計算式，然后仔細觀察這些方程找出隱藏的關鍵信息，才能解出題目.這時候如果學生的草稿紙上的計算過程比較整齊、干凈醒目，那么發現已知條件中暗含的關鍵信息就比較容易，更不會發生抄錯數字、弄錯符號等現象，解題過程自然一帆風順.

但是，也正因為草稿紙是不用給別人看的，所以很多學生的草稿紙就亂成一團，做題的時候自然也就顧此失彼，很難做到全面把握題目信息，丟分也就在所難免.

因此，學生在平時的學習、做題過程中就應當書寫工整，卷面整潔，哪怕是草稿紙上的演算也要整整齊齊、有條有理.

3.3 養成專心做題的習慣

學生應當重視平時的練習和作業，把它們當作考試看待——只要開始做題，就必須聚精會神.在做題時，要清理桌面不相關的物品，左手拿直尺，右手拿筆，書寫時靠左邊開始，等號、分數線都用直尺來畫，保持卷面整齊干凈.

心理學研究發現，等號、分數線等符號都用直尺來畫，雖然放慢了書寫的速度，但卻提高了學生的有意注意，讓學生能把注意力集中在做題上，提高準確率.筆者在長期教學實踐中也發現，用這樣的方法真的能改變學生所謂“粗心”的習慣，提高做題的準確率.

3.4 養成使用“錯題本”的習慣

錯題反映的是學生的弱項，往往是導致學生丟分的“隱形殺手”.在教學中筆者發現學生在更正錯題時大多數都是寫在原題的旁邊，這些錯題更正的分布七零八落，可能在某次考試的試卷上，也可能在某次作業本上，甚至可能被學生弄丟了.如果能把每次的錯題收集起來，并且逐一進行更正，這樣一方面為學生提供了一個個性化的復習資料，另一方面也起到了強化的作用，提醒學生在這里曾經出現錯誤，如果再次碰到一定要注意，不能犯同樣的錯誤.

3.5 養成整齊有序的生活習慣

如果一個學生生活在雜亂無章的環境中，什么東西都可以亂放，沒有穩定的作息習慣，就容易養成粗心、馬虎、無序的生活習慣.所以，家長要幫助學生創造一種有序的生活，做什么事情都要盡量有規律.養成良好的做事習慣，并把它遷移到學習中，就能夠有效減少上面提到的各種“粗心”現象.

4 有“三心”才能有“細心”

“粗心”是一種壞習慣，每一個人經過努力都能改掉這個壞習慣.只要學生能夠樹立“信心”，下定“決心”，同時“耐心”堅持，慢慢地就能把這個壞毛病用“細心”的好習慣替換掉.“細心”的習慣一旦養出，“粗心”將徹底離開你.

面對較難、思考性較強的題目，學生更要有克服困難的“信心”，“細心”分析題目，找到與知識關聯之處，找出入口點，從而成功解答題目.筆者在做題思路不通時，常重新讀題，并畫相關圖形，往往就可以找到解題思路.

可以這么說：

不是“粗心”，而是因為對知識的基本概念不清楚;

不是“粗心”，而是因為專注力不集中;

不是“粗心”，而是因為書寫習慣不好;

不是“粗心”，而是因為閱讀理解能力有待提高.

所以，放棄“粗心”這樣的說法吧！放棄這個觀點之后，我們才有可能認真查找原因，制訂訓練的計劃，獲得真正的提升，且提升的不僅僅是成績，還包括審視問題的角度，解決問題的策略、行動力和意志力.

【參考文獻】

[1]孫東芝，于曼，李美麗.新課程背景下初中數學審題習慣的培養[J].中學數學，2020（22）：94-95.

[2]王國林.基于高中數學習慣性錯誤透視學習習慣培養[J].中學教學參考，2020（30）：28-30.

[3]關存杰.如何在高中課堂教學中培養學生的良好數學思維習慣[J].數學大世界（下旬），2020（9）：4.