從一道高考題的變遷看阿基米德三角形性質及其定理的演繹

李真 徐水龍

【摘要】 阿基米德三角形有著豐富的內涵、深刻的背景，至今依然是高考命題者的青睞，其有關性質仍是命題專家的熱點素材.本文從一道2008年山東高考題開始，探索阿基米德三角形定理的由來，演繹其性質應用.

【關鍵詞】阿基米德三角形定理;性質演繹

阿基米德是古希臘偉大的物理學家、數學家、天文學家和機械發明家.拋物線的弦與過弦的端點的兩條切線所圍成的三角形，常被稱為阿基米德三角形.阿基米德三角形以其豐富的內涵、深刻的背景，在數學發展的歷史長河中不斷發出閃耀的光芒，至今依然是高考命題者的青睞，其有關性質也成為命題專家的熱點素材.下面舉例說明.

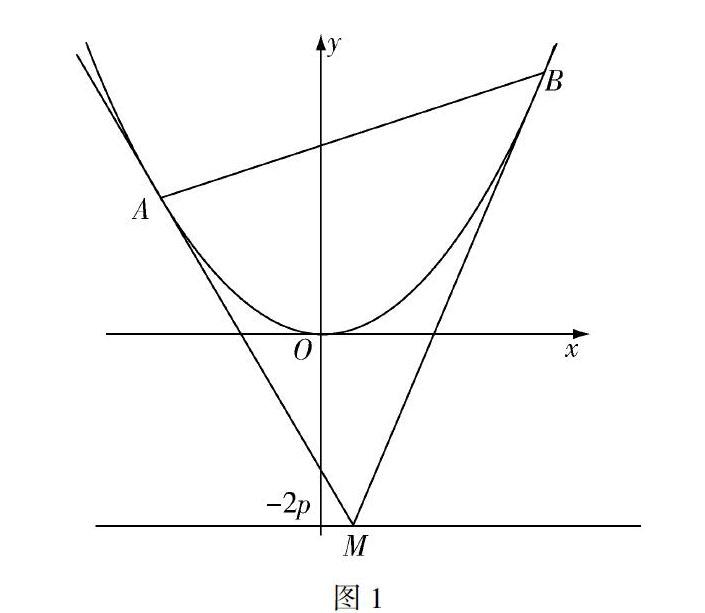
這是2008年理科第22題（部分）.如圖1，設拋物線方程為x2=2py （p>0），M為直線 y=-2p上任意一點，過M引拋物線的切線，切點分別為A，B.求證：A，M，B三點的橫坐標成等差數列;

本題涉及阿基米德三角形，考查了阿基米德三角形的有關性質.

（1）求直線AB與y軸的交點N的坐標;

（2）若E為拋物線弧AB上的動點，拋物線在E點處的切線與△MAB的邊MA，MB分別交于點C，D，記λ=S△EABS△MCD，問：λ是否為定值？若是，求出該定值;若不是，請說明理由.

問題（1）求直線AB與y軸的交點坐標，由前面分析可知直線AB的方程，我們只需令y=0即可，直線AB與y軸的交點坐標為N（0，2p），是個定點.于是我們猜想弦AB繞著N點轉動，M點的軌跡是什么？我們設M（x，y），有x=x1+x22，y=x1x22p，由A，N，B三點共線，得y=-2p，顯然它是一條直線.我們進一步猜想弦AB繞著點G（xG，yG）轉動，M點的軌跡是什么？由A，G，B三點共線，得（x1+x2）xG-2pyG-x1x2=0，將x1+x2=x，x1x2=y代入，得xGx-p（y+yG）=0，它仍然是一條直線.于是我們得到阿基米德三角形的性質2.

性質2 若阿基米德三角形的底邊AB過拋物線內定點G（xG，yG），則另一頂點M的軌跡為一條直線，其方程為xGx-p（y+yG）=0.

特別地，當定點G在y軸上時，性質2還有以下推論.

阿基米德三角形定理 拋物線和它的一條弦所圍成的封閉圖形的面積，等于拋物線的弦與過弦的端點的兩條切線所圍成的三角形面積的三分之二.

阿基米德三角形背景深刻，內涵豐富，我們從一道高考題演繹了阿基米德三角形的性質及其定理.

【參考文獻】

[1]方亞斌.千年古圖蘊藏題庫：阿基米德三角形演繹高考題[J].中學教研（數學），2017（7）：33-39.

[2]邵志明，陳克勤.高考試題中的阿基米德三角形[J].數學通報，2008（9）：39-46.

[3]劉瑞美.對一道2011年高考圓錐曲線問題的探究[J].數學通迅，2012（5）.