解線性方程組的經(jīng)典迭代算法

程軍 朱彪

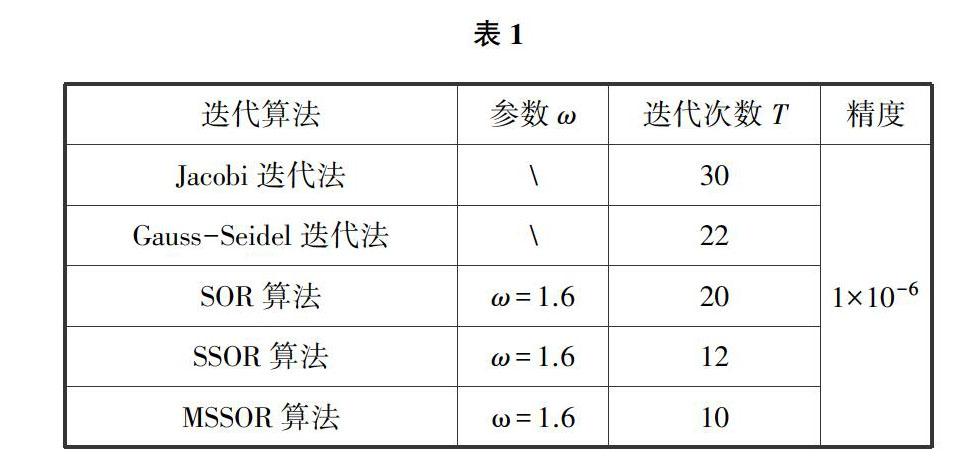
【摘要】本文介紹了分裂法解線性方程組的一些迭代算法，然后通過改變系數(shù)矩陣A的分裂形式和對一些算法進行改進得到了新的算法.研究得知，通過改變系數(shù)矩陣A的分裂形式得到的新算法具有更好的收斂性，改進的SSOR算法和MSSOR算法有了更快的收斂速度.最后通過數(shù)值實例驗證了這兩種算法在有些情況下確實可以更有效地解決問題.

【關(guān)鍵詞】線性方程組;迭代算法;矩陣分裂;收斂速度

目前，經(jīng)過很多學者長期不懈的研究，得到了比較成熟、理想的關(guān)于線性方程組的迭代解法，這些解法都是基于矩陣的分裂而得到的.在實際解決具體問題過程中，我們依然面臨著許多不同的困難，針對這些問題，很多人都做了大量的研究.筆者在研究這些線性方程組的問題時，通過對這些迭代算法進行相應(yīng)的改進，得到了兩種新的算法.同時筆者對這兩種新算法的收斂性進行了詳細的證明，通過相應(yīng)的數(shù)值驗證了該算法在解決某些具體問題時所具有的優(yōu)勢.

1 迭代法原理

【參考文獻】

[1]吳世良，李翠霞，張理濤.特殊線性系統(tǒng)的數(shù)值迭代算法[M].北京：科學出版社，2015.

[2]張理濤，吳世良.線性方程組的高效迭代算法[M].北京：科學出版社，2014.

[3]邵新慧.大型線性方程組的迭代解法[D].東北大學博士學論文，2009.

[4]程云鵬.矩陣理論[M].西安：西北工業(yè)大學出版社，2005.

[5]張理濤.線性方程組和鞍點問題的迭代法與預(yù)處理技術(shù)研究[D].電子科技大學博士學位論文，2009.

[6]徐樹方，高立.數(shù)值線性代數(shù) [M].北京：北京大學出版社，2000.

[7]陳金雄.L-矩陣的預(yù)條件方法及其比較定理[J].云南民族大學學報（自然科學版），2013（3）.