面板計數數據的非參數樣條估計*

上海交通大學生命科學技術學院生物信息與生物統計系(200240) 秦 飛 俞章盛

【提 要】 目的 建立更為一般化的面板計數數據模型，既包含具有時變效應的協變量又包含具有非參數效應的協變量。方法 使用偽似然樣條估計方法及全似然樣條估計方法，并通過數值模擬定性和定量地比較這兩種方法。結果 兩估計方法在樣本量為200時都具有很小的偏差和均方誤差(MSE)；全似然樣條估計方法的偏差和MSE更小(比偽似然樣條估計方法的MSE小約35%)，但計算時間遠遠超過偽似然樣條估計方法(約是其200倍)；兩種估計方法用于小兒哮喘數據后得到了相似的估計結果，揭示了白細胞介素IL-9的時變效應及白細胞介素IL-5的非參數效應。結論 綜合MSE及計算時間，在此模型下本研究更推薦使用偽似然樣條估計方法。

面板計數數據經常出現在電子醫療病例、臨床試驗、流行病學研究中。對于面板計數數據，研究者僅調查到在兩次相鄰的觀測時間點間復發性事件發生的次數，但未調查到復發性事件發生的具體時刻。一個典型的例子可見于小兒哮喘研究[1]。在此研究中，研究人員對105個小兒哮喘病患者連續跟蹤了5年，通過電話隨訪獲得截至到此刻小兒哮喘復發的次數，但未調查到復發的具體時刻，所以收集到的數據為面板計數數據。

在對面板計數數據的建模方面，Zhao等[2-3]先后建立了具有時變效應及具有非參數效應協變量的面板計數數據模型，但尚未有研究在一個面板計數數據模型中同時考慮到這兩者，而這種情況在實際應用中是可能出現的，比如Cai等[4]就在Cox模型中同時包括了具有時變效應及具有非參數效應的協變量。在估計方面，Zhao等[2-3]僅采用了偽似然函數下的樣條估計方法，但沒有采用全似然函數下的樣條估計方法。因此，本文將建立同時含有時變效應及非參數效應協變量的面板計數數據模型，采用偽似然樣條估計及全似然樣條估計的方法并對其進行對比，最后將此方法應用于小兒哮喘研究中[1]。

模型及估計

1.模型

對于面板計數數據，研究者可以觀測到n個獨立的樣本Ui=(Ki，Ti，N(i)，Xi，Zi)，i=1，2，…，n，其中Ki為觀測次數，Ti={Ti，1，Ti，2，…，Ti，Ki}為觀測時間點，N(i)={N(Ti，1)，N(Ti，2)，…，N(Ti，Ki)}為面板計數值，Xi=(Xi，1，Xi，2，…，Xi，p)T為具有時變效應的協變量，Zi=(Zi，1，Zi，2，…，Zi，q)T為具有非參數效應的協變量。類似于其他非參數模型，本文假定某個協變量是具有時變效應還是非參數效應是提前設定好的。本文建立以下非參數模型：

E[N(i)(t)]=Λ0(t)·exp[(β1(t)T·Xi+β2(Zi)]

(1)

其中，Λ0(t)為單調非減的非負函數，β1(t)=(β1，1(t)，β1，2(t)，…，β1，p(t))T為時變系數，β2(Zi)=β2，1(Zi，1)+β2，2(Zi，2)+…+β2，q(Zi，q)為非參數效應。本文僅呈現當p=q=1時的情形，本文的估計方法很容易拓展到p，q>1的情形。

2.樣條函數

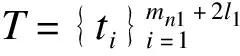
(2)

(3)

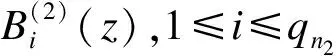
(4)

3.偽似然估計

正如Zhang等[5-6，14-15]所述，首先假設潛在的計數過程{N(t)：t≥0}為非齊次的泊松過程，然后忽略每個個體的計數數據{N(Ti，1)，N(Ti，2)，…，N(Ti，Ki)}之間的相關性從而得到的偽似然估計量通常具有漸近正態性和相合性。參照Zhang等[5-6，14-15]的思路，本文建立模型(1)的偽似然函數如下：

L(1)=P[N(T1，1)=N1，1，N(T1，2)=N1，2，…，N(T1，K1)=N1，K1，…，N(Tn，1)=Nn，1，…]

對L(1)取對數并忽略無關項，然后將樣條近似式(2)～(4)代入，得到以下對數偽似然函數：

(5)

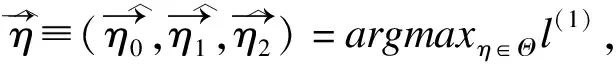
4.全似然估計

如Zhang等[5-6，14-15]所述，全似然估計量通常要比偽似然估計量估得更準但同時計算量更大。本文也探討了全似然估計在模型(1)下的表現。全似然估計量是通過首先假設潛在的計數過程為非齊次泊松過程，然后利用面板計數數據增量間的獨立性而構造。本文建立模型(1)的全似然估計函數如下：

exp[-[Λ0(Ti，j)·exp(β1(Ti，j)·Xi+β2(Zi))-Λ0(Ti，j-1)·

exp(β1(Ti，j-1)·Xi+β2(Zi))]]}

其中，Λ0(Ti，0)≡0，Ni，0≡0。對L(2)取對數忽略并無關項，然后將樣條近似式(2)～(4)代入，得到以下對數全似然函數：

(6)

同樣地，極大化式(6)便可得到參數的全似然估計。這一過程仍可通過相同的R函數constrOptim()來實現。

模擬研究

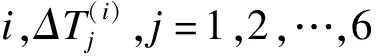
N(Ti，j)-N(Ti，j-1)～Po{Λ0(Ti，j)·exp[β1(Ti，j)·Xi+β2(Zi)]-Λ0(Ti，j-1)·exp[β1(Ti，j-1)·Xi+β2(Zi)]}

其中j=1，…，Ki，Ti，0≡0，N(Ti，0)≡0，Λ0(0)≡0。本文對真實函數設置以下兩種情形：

情形1：Λ0(t)=t+1，β1(t)=1.5·sin(0.05·πt)，β2(z)=sin(πz)；

情形2：Λ0(t)=t+1，β1(t)=0.15·t，β2(z)=sin(2πz)·I(z≤0.5)+0.5·sin(2πz)，其中I(·)為示性函數。可以看到情形2要比情形1更為復雜。

本文設置樣本量為50及200，產生500次蒙特卡洛數據。參照Lu等[5-6]的做法，本文使用三次樣條，樣條的內部節點數設置為6，采用分位數的方法放置節點，即選擇所有不同觀測時間點的k/(m+1)分位點(k=0，1，…，m+1)為這m+2個節點的放置位置。

圖1展示了情形1下樣本量為50時對這三個函數Λ0(t)，β1(t)，β2(z)500次估計的均值曲線及2.5%，97.5%分位數曲線。從圖1可以看出，這兩種方法的估計結果都存在一定的偏離，也如前文所預料，這三個函數的全似然估計的均值曲線更接近于真實曲線，且置信區間更窄。當樣本量增大為200時，所有的均值曲線相對樣本量為50時都更接近真實曲線且置信區間更窄，全似然估計方法此時仍舊估得更準且置信區間更窄，但同時也注意到此時兩方法的均值曲線都幾乎跟真實曲線重合(圖2)。

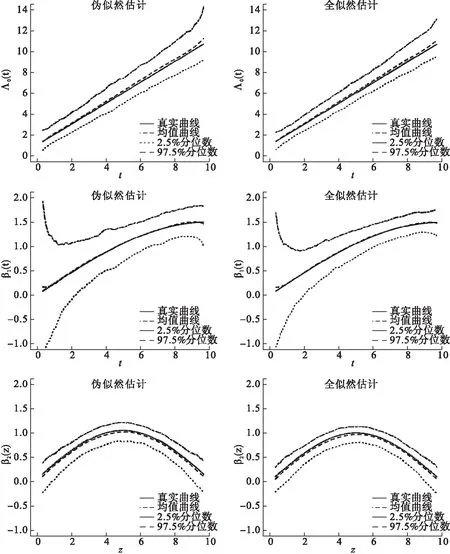
圖1 情形1，樣本量為50時的估計結果

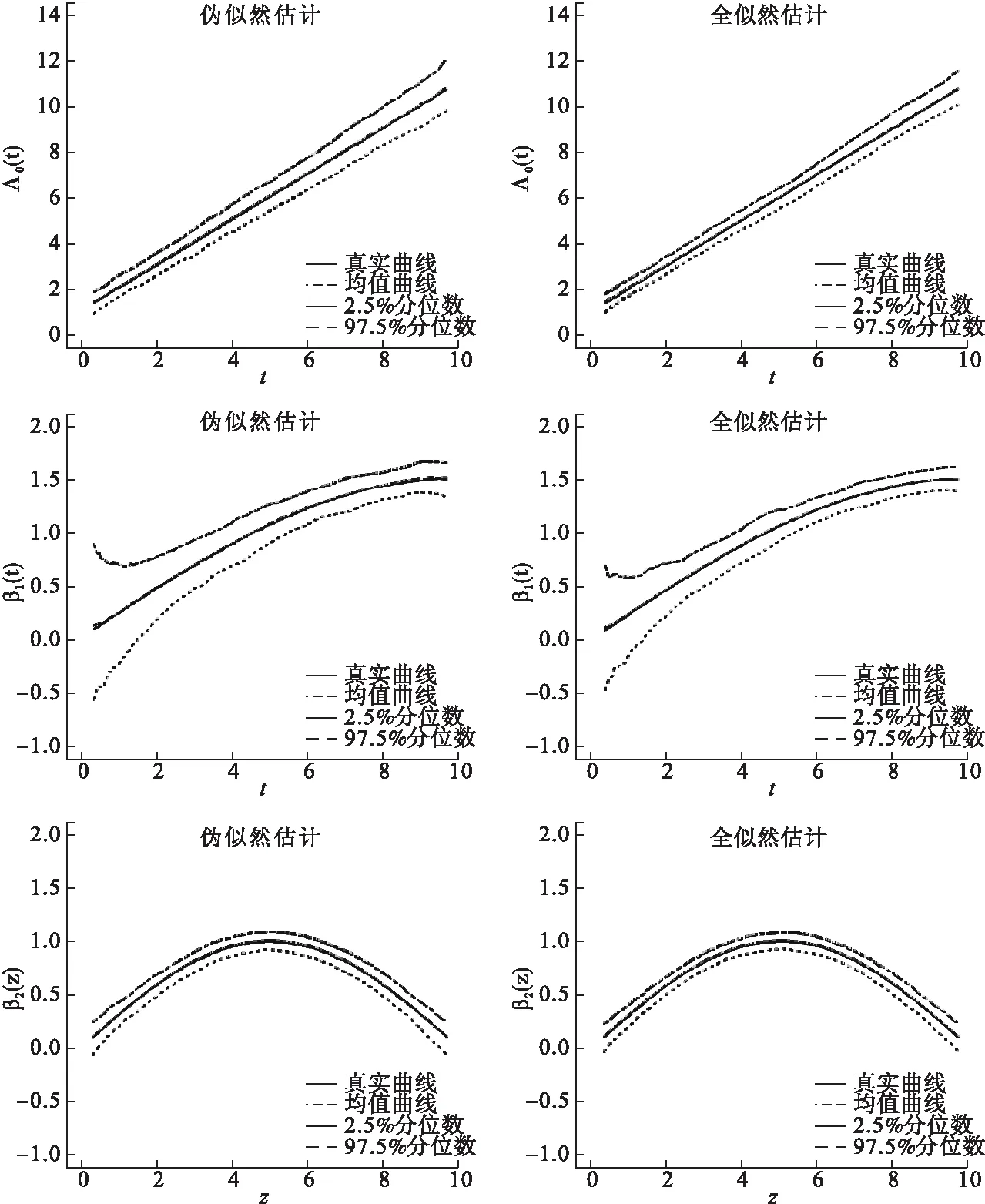
圖2 情形1，樣本量為200時的估計結果

本文也對這兩種估計量進行了定量比較。從表1可以看出，當樣本量為50時，全似然估計下這三個函數的估計偏差、均方誤差均小于偽似然估計，但偽似然估計的計算時間遠遠小于全似然估計。當樣本量增大為200時，這兩種估計下函數的估計偏差、均方誤差都大大減小，全似然估計方法仍估得更準，但同時計算時間方面偽似然估計方法仍遠具優勢，并且也注意到此時兩估計方法的偏差幾乎可以忽略。情形2的模擬結果和結論類似情形1，由于篇幅有限，本文沒有展示。由于在接下來的實際應用中樣本量為105，本文還做了上述兩情形下在樣本量為100時的模擬，此時的估計偏差、均方誤差及計算時間介于樣本量為50時的結果和樣本量為200時的結果之間，得到的結論也類似(由于篇幅有限，未展示)。總之，就估計的準確性和穩定性而言，全似然估計方法優于偽似然估計方法，前者的TMSE比后者小約35%。但就計算時間而言，偽似然估計占絕對優勢(全似然估計計算時間約為偽似然的200倍)，再加上當樣本量為200時，偽似然估計量已非常接近真實函數，所以在模型(1)下，本文推薦使用偽似然估計方法。

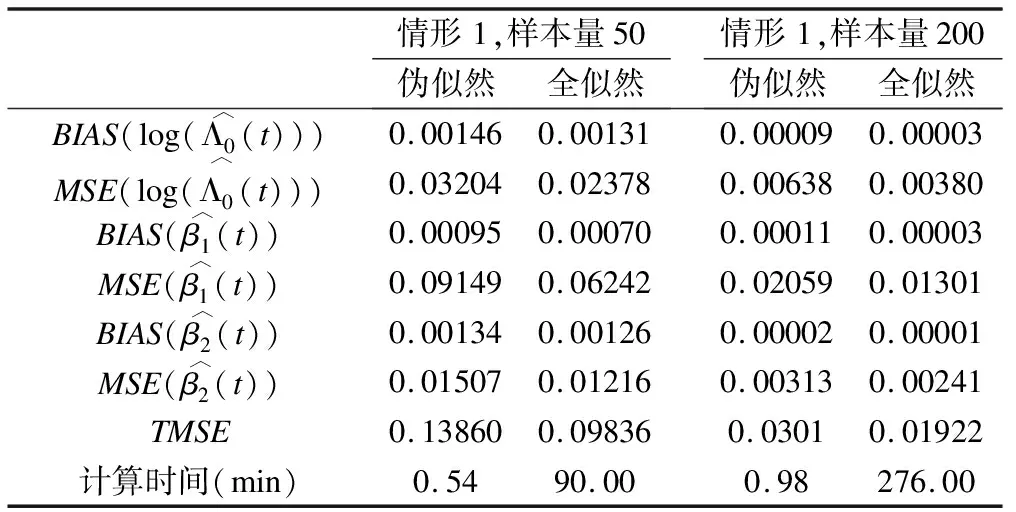
表1 情形1下兩種估計量的定量比較結果

實例應用

本部分把前文介紹的方法應用到小兒哮喘研究中，該研究的總體描述可參考文獻[1]。該研究旨在探究免疫因子特征和小兒哮喘之間的關系，納入了105名小兒哮喘患者，平均入組年齡為10.9月，50.5%的患者是女性，9.5%的患者母親在懷孕時抽煙。

白細胞介素IL-9是CD4+輔助細胞分泌的一種細胞因子，對哮喘小鼠模型的遺傳學研究表明，該細胞因子是支氣管高反應性發病的決定性因素[16]。根據臨床經驗，有很多因素都會影響到小兒哮喘而且它們的影響效果會隨著時間的變化而變化，因此本文設定IL-9具有時變效應。此外，另一種白細胞介素IL-5一直與過敏性鼻炎、哮喘等多種變應性疾病相關[17]。根據Zhao等[3]的研究結果，IL-5具有明顯的非參數效應。因此，在本文的面板計數數據模型中包括性別及是否吸煙這兩個協變量后，本文用偽似然估計和全似然估計這兩種方法來估計IL-9的時變效應及IL-5的非參數效應。

本文使用三次樣條來估計模型中的未知函數；使用AIC準則(AIC=-2·l(η)+2k)來選擇內部節點個數，其中l(η)為對數偽似然函數值或者對數全似然函數值，k為模型中參數的個數；和模擬研究類似，節點的位置選取依舊使用分位數的方法。對于偽似然估計，本研究選擇的節點數為7，對于全似然估計，選擇到的節點數為6，對時變效應β1(t)和非參數效應β2(z)的估計結果如圖3所示。從圖3可以看出，由于使用的內部節點數更多，偽似然估計方法對β1(t)及β2(z)的估計曲線更震蕩些，但總體趨勢和全似然估計方法得到的曲線十分相似。這兩種估計結果都揭示了IL-9對小兒哮喘效應的時變性，即在30個月齡之前，效應隨著年齡的增大而增大，但其后效應基本趨于平穩。同之前Zhao等[3]的研究結果一致，IL-5的效應仍舊是非參數的，效應隨著IL-5值的增大而增大。本研究中模擬及實例應用部分是在R軟件中實施的，實例應用部分的代碼可通過以下ftp地址獲得：ftp：//public.sjtu.edu.cn/(用戶名yuzhangsheng，密碼public)。

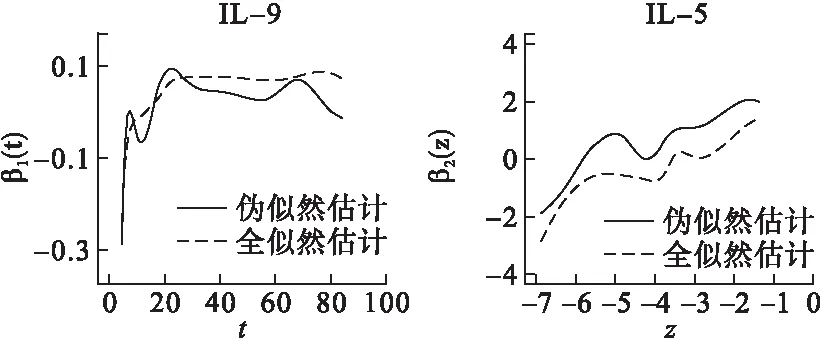
圖3 小兒哮喘研究中對白細胞介素IL-9及IL-5的估計結果

小 結

本文建立了更為一般化的面板計數數據模型，其既包含具有時變效應的協變量，也包含具有非參數效應的協變量；本文使用了偽似然樣條估計方法和全似然樣條估計方法，并將這兩種估計方法進行了對比；最后分析了小兒哮喘研究數據。

在模擬研究部分，發現當樣本量為50和100時，這兩種估計方法都存在一定的偏差，但全似然樣條估計方法的偏差和均方誤差更小；同時由于全似然函數更為復雜，所以全似然樣條估計方法具有更長的計算時間。當樣本量增大到200時，兩種估計方法都具有可以忽略的偏差，且全似然樣條估計方法仍舊具有更小的偏差和均方誤差，但同時計算時間也長得多。綜合均方誤差和計算時間，且考慮到當樣本量為200時偽似然樣條估計方法已較準確，本文推薦在類似的模型中使用偽似然樣條估計方法。

在實例應用部分，這兩種估計方法得到了類似的估計結果，都揭示了白細胞介素IL-9的時變效應及白細胞介素IL-5的非參數效應，此結論也跟之前的研究[3]一致。探究在本文模型下兩種估計方法的理論性質，研究更為高效的算法將是我們未來的研究方向。