“深備”的實踐與思考

周雯

摘要：深度備課作為課堂教學的第一環(huán)節(jié)，是提高數(shù)學教學效果的重要途徑。本文結合具體教學案例，從學生原有數(shù)學認知上的適度提升、學生思維生長點的精準把握、知識邏輯結構的重新梳理、知識學習實用性與必要性的感受、數(shù)學知識內在文化的歷史溯源等方面探索如何有效開展深度備課。

關鍵詞：本真心 深備 備學生 備知識內容

裴光亞先生曾說：“教育價值是教學設計的靈魂。”深備，顧名思義，就是深度備課。深備，需要備學生的認知、學情、年齡特點、常有的思維特點等，做好充分的預設;深備，需要備教材內容，如這一知識的歷史史源是什么，前后位知識是什么，與前后位知識的邏輯關系如何？下面筆者就在深備中的幾點做法與同人們交流一下，請斧正。

一、“深備”——學生原有數(shù)學認知上的適度提升

《義務教育數(shù)學課程標準》指出：數(shù)學教學活動必須建立在學生的認知發(fā)展水平和已有的知識經(jīng)驗基礎之上。如果初中教學內容只是小學內容的再現(xiàn)，那就是“淺備”，這樣的課堂一定是低效、無趣、無挑戰(zhàn)的。教師要把學生小學時對知識的直觀感受提升到理性認識層面上來，為此要進行“深備”。

案例1：《一元一次方程及其解法》

此課是滬科版七年級上冊第三章第一節(jié)第一課時的內容，教學目標是通過兩個實際問題情境，體會列方程解決問題的必要性和簡便性，體會方程是刻畫現(xiàn)實世界的一個有效數(shù)學模型。學生在小學階段已經(jīng)學習過等式基本性質1、2，也會熟練運用等式基本性質解方程，如果花費過多時間再次學習等式基本性質，課堂節(jié)奏將不會流暢。而且初中又增加了對稱性、傳遞性等內容。基于此，教學設計如下：學習完一元一次方程概念之后，讓學生求解一個一元一次方程。有了小學的認知基礎，大部分學生能成功求解。重點是引導學生從數(shù)理角度分析每一步的依據(jù)，升華理論知識，再通過巧妙的設計讓學生體會對稱性的實用性，讓等式基本性質的運用有抓手。深備，在原有認知上適度提升，找準小初銜接點，找準所學知識的前位知識，讓課堂本真、高效。

二、“深備”——學生思維生長點的精準把握

教師如同醫(yī)生，有經(jīng)驗的醫(yī)生能把病人的病根找到，有經(jīng)驗的教師能將學生腦中模糊的、錯誤的認識找到，盡管不能“藥到病除”，但這樣的數(shù)學課更有數(shù)學味。讓學生的數(shù)學思維活躍起來，必須通過問題實現(xiàn)。

海莫斯說：“問題是數(shù)學的心臟。”設計什么樣的問題？如何精心設計？怎么提問？何時提問？達到什么目的？這必須要找準學生的思維生長點，充分預設，讓知識生成得自然。

案例2：《多邊形的內角和》

這節(jié)課的前一部分內容是多邊形的定義及相關概念，這里就可以讓學生基于四邊形的定義自己去給多邊形下定義，這就是學生的思維生長點。學生會說：“由不在同一條直線上的若干條線段首尾順次相接組成的封閉圖形叫作多邊形。”按照學生類比得出的結論，再次預設，基于學生思維，進行教學設計：準備好教具（4根細吸管，用線穿過吸管，剛好首尾依次相接），沿著對角線折起兩條線段，是四邊形嗎？學生會意識到定義的漏洞，并強調是在平面內！于是得出多邊形的定義。

進行如何求多邊形的內角和教學設計時，也需要尋找學生的思維生長點，那就是求四邊形ABCD的內角和。

學生最容易想到的辦法是連接對角線AC或BD，將四邊形的內角和轉化成三角形的內角和。基于此，展示連接AC、BD連接后的圖，追問：你能用其他方法證明嗎？

根據(jù)學生的敘述用幾何畫板展示：

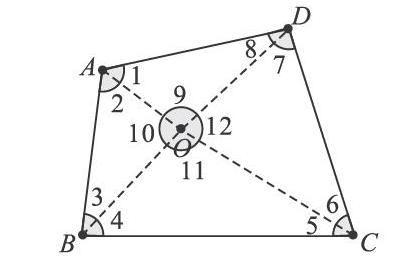
學生的回答就是學生的思維生長點。再提問：對角線的交點很特殊，如果這個點不是特殊點，它只是內部的任意一點，你能證明嗎？于是得到圖1。

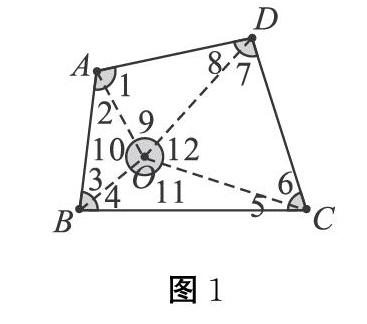
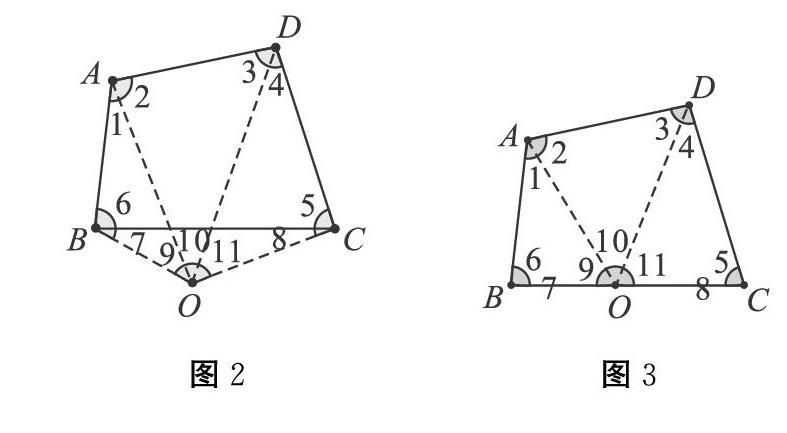
學生能感受到證明過程同理。進而提問：這個點O還能在哪呢？由點在外部或者在邊上，得到圖2、圖3。

基于將四邊形問題轉化為三角形問題的這么多方法，再提問：你認為哪種方法最簡便？再基于求四邊形內角和的經(jīng)驗，繼續(xù)求五邊形、六邊形、n邊形的內角和。

最后，基于n邊形內角和的多種求法，在觀察總結中完成下表。

有的老師是為了填表而填表，一開始就呈現(xiàn)表格，一味要求把內容填上。其實填表只是為了幫助學生總結結論，表格只是工具，恰當?shù)爻尸F(xiàn)表格需要老師找準學生的思維生長點。

三、“深備”——知識邏輯結構的重新梳理

知識的前因后果是什么，它的邏輯起點是什么？怎么設計更有邏輯性？整體架構是什么樣？對于這些問題，教師要做到胸有成竹，統(tǒng)籌全局。

案例3：《線段的長短比較》

為什么線段可以進行長短比較？用比個子類比，到底比的是線段的什么？比線段比的是長度。正因為有長有短，所以兩個量之間才可以進行比較。而大小關系有幾種？三種。這三種關系又是如何體現(xiàn)在兩條線段比較上的？體現(xiàn)在書寫符號上，如AB>CD，指的是AB的線段長度大于CD。

中點知識為什么出現(xiàn)在《線段的長短比較》這一節(jié)呢？其實，該知識點仍然涉及線段長短比較。當線段AB上有一點C，必然有AC，BC這兩條線段，當AC=BC時，C即為中點。因此，中點的邏輯起點仍是線段長短比較。

關于基本事實“兩點之間線段最短”，從A到B有直的線，也有曲的線，這不正體現(xiàn)了直的線和曲的線的長短比較嗎？這相當于線段長短比較的延伸。理解邏輯起點，構建正確的邏輯框架，有助于教學思路更清晰。

四、“深備”——知識學習的實用性與必要性

很多時候，課堂教學如果沒有有效的抓手，將顯得蒼白枯燥。因此，讓學生充分感受知識學習的實用性與必要性，是備課的主要內容。

案例4：《比例線段》

學生在小學階段已經(jīng)學過內外項積相等，由x∶y=3∶2得到2x=3y;反之，根據(jù)2x=3y，求x∶y等于多少時，大部分學生總會出錯。

x：y等于多少？根據(jù)內項積等于外項積，應該等于3∶2。寫3的時候，要明確告訴學生緊盯3y。那若ab=cd，得到哪些比例式呢？學生可能會很快寫出ac=db，或者ad=cb，當追問“還有不同的比例式嗎”，學生可能會感覺能寫出很多情況，但又覺得寫其他的比例式?jīng)]什么用，都差不多。

老師可以畫個典型圖，讓學生思考：若是要證明AB×CD=EF×GH，怎么證呢？告訴學生：先要學會將乘積式化成比例式，根據(jù)圖形特點，將哪條線段放在第一項寫，就決定了你后面三項怎么比。

講解總要有個合理的載體，讓學生覺得有必要學，體會到一節(jié)課所學的知識究竟怎么用。哪怕只是為了會解題，也要讓學生在課堂上親自解一解。

因要讓計算更簡便，需要學習運算律和總結公式;因生活出現(xiàn)了負數(shù)，不得不定義有理數(shù);因存在無理數(shù)，不得不擴充到實數(shù);因相等學習等式;因不等學習不等式;等等。這些都體現(xiàn)了知識學習的實用性與必要性。

五、“深備”——數(shù)學知識內在文化的歷史溯源

數(shù)學教學不僅要教知識，還要關注知識內在文化的聯(lián)系。知識教學其實也是文化教學，更多地了解歷史發(fā)展故事對教學有很大的幫助。

案例5：《用字母表示數(shù)》

七年級上冊第二章《用字母表示數(shù)》，是代數(shù)的基礎、基石。要知道，從用文字來表示一個代數(shù)問題的解法，即修辭代數(shù)，到用字母表示未知數(shù)，即縮略代數(shù)，經(jīng)歷了2000多年。再從縮略代數(shù)到符號代數(shù)，即用字母表示任意數(shù)，又經(jīng)歷了1300年。我們在教學時，一節(jié)課時間就想讓學生理解古數(shù)學家需要幾千年才弄懂的知識，實在太不容易了。筆者在教學用字母表示數(shù)這一知識時，所帶的兩個班學生，只有很少一部分人能運用用字母表示未知數(shù)，他們想要真正理解用字母表示數(shù)、表示任意數(shù)，肯定是個緩慢的過程。

數(shù)學史是數(shù)學教師的重要教學資源。數(shù)學教師可以針對某個特定的知識點，融入相關的數(shù)學史，同時這也可以緩解教學壓力。

深度備課，要備學生的學情、思維生長點，備知識的邏輯結構、學習必要性與歷史文化。若只是“淺備”知識，終究只能是教書匠！