巧設思維障礙 引發深度思考

陳光明

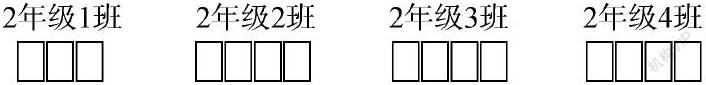
摘 要：在教學中設計富有趣味性、挑戰性和開放性的問題，是引導學生進入深度思考的基礎。為此，筆者常常在教學過程中故意制造一些“麻煩”，設置一些“障礙”，“逼著”學生“跳一跳，摘桃子”，帶著學生“多走一些彎路看風景”，獲得良好的教學效果。

關鍵詞：巧設障礙;深度思考;隱藏關鍵數據;掩蓋計算過程;不給足夠學具

在教學實踐中可以發現：問題的挑戰性，直接影響著探究空間的大小，也影響著學生探究的興趣和熱情。在教學中設計富有趣味、又不失挑戰性的開放性問題情境，是引導學生進入深度思考的基礎。為了更好地激發學生的探究熱情，引發深度思考，筆者常常在教學過程中故意制造一些“麻煩”，設置一些“障礙”，“逼著”學生“跳一跳，摘桃子”“多走一些彎路看風景”，獲得良好的教學效果。

一、 隱藏關鍵數據，點燃思維火花

在引導學生探究規律時，免不了要借助各種數據信息。有時為了激發學生的思維，筆者故意先將問題中的關鍵數據隱藏起來，反而收到意想不到的效果。例如，在教學《萬以內數的大小比較》時，筆者沒有在一開始就為學生提供完整的數據信息，而是根據“大小比較”的三個要點，先將數據信息隱藏，然后分層次逐步呈現，來引導學生經歷探究萬以內數的比較過程，使學生不僅學會大小比較的方法，還明白其中的道理。具體過程如下：

環節一：位數不同，比位數。

師：二年級四個班級開展“回收飲料瓶，爭當環保者”活動。哪個班級收集的飲料瓶最多，將獲得“環保先鋒”的榮譽稱號。要想知道哪個班級收集的飲料瓶最多，你需要了解哪些信息？

生：需要知道每個班級收集的飲料瓶數量。

屏幕上出示二年級四個班級收集的飲料瓶“數量”，可是將所有的數字，用卡片遮住，只能看出每個數有幾位數。

師：你會比較它們的大小嗎？

所有學生一時陷入沉思，但不久就有學生舉手。

生：2年級1班收集的飲料瓶數量是最少的。

師：為什么沒有告訴你具體的數量，你就能知道2年級1班是最少的，你能說明其中的道理嗎？

生：2年級1班收集的飲料瓶數量是三位數，其他三個班級收集的飲料瓶數量都是四位數，三位數比四位數小。

師：為什么三位數就一定比四位數小呢？

經過學生獨立思考后，再組織討論交流，使學生明白：三位數最多是999，而四位數最少是1000，所以三位數一定比四位數小。

環節二：位數相同，先比最高位。

師：其他三個班級的位數都相同，該如何比較它們的大小呢？

生：需要翻開遮蓋在數字上的卡片。

師：如果現在只給你三次機會，讓你翻開三張數字卡片，你會選擇哪三張？

經過討論，學生一致認為應該翻開三張“千位”上的卡片。

師：現在你又有什么新的發現？

生：我知道2年級2班收集的飲料瓶一定比2年級3班和2年級4班少。

師：為什么只憑三張卡片，你就能確定2年級2班比其他兩個班級少？

通過討論交流，使學生明白：2班收集的飲料瓶最多只能是1999，而3班和4班最少也有2000，只要看千位上的數就能比較它們的大小。

環節三：最高位相同，依次往下比。

師：現在只剩下3班和4班了，哪到底誰多誰少呢？你還需要知道什么信息？

生：只要知道它們百位上的數就可以。

教師出示3班和4班的“百位”上的數。

師：現在你能比較嗎？

生1：3班收集的飲料瓶比4班多。

生2：4班最多只能是2199，而3班最少是2300。

通過先將數據隱藏，然后隨著問題的探究來逐步呈現。這樣極大地增加了探究的空間，為深入理解大小比較的方法和道理提供了有效的情境。同時也充分“吊足”學生的胃口，使學生在經歷“探案”般的探索過程中，注意力高度集中，思維被不斷引向深入。使學生在沉浸式的思考中主動獲得知識與技能，不斷發展思維能力，充分享受成功的喜悅。

二、 掩蓋計算過程，探究錯誤原因

學習的過程實際上就是一個不斷修正錯誤的過程。如何正確處理學生在學習過程中出現的錯誤，往往考驗著一個教師的教學藝術水平。在教學《兩位數乘兩位數》時，練習中發現學生的一個錯例。筆者故意將該生的計算過程用卡紙遮掉，問學生：“你們覺得，這道題的計算結果正確嗎？說說你判斷的依據。”

生1：這道題的計算是錯誤的，因為20×10就等于200，而24比20大，12比10大，所以正確的積一定比200大。

師：這位同學懂得用估算的方法來判斷結果是否正確，他的方法值得我們每一位同學學習。

生2：兩個因數的個位分別是“4”和“2”，所以積的個位一定是“8”，而他計算的結果個位上的數字是“2”，所以我斷定他算錯了。

師：這位同學懂得根據因數和積個位上的數來判斷計算的結果，也是一種不錯的方法。那么，你們猜猜看他可能錯在了哪里呢？

生3：我看到他的最后結果是兩位數，所以我覺得他在計算10乘24時，積的最低位沒有從十位寫起，而是從個位寫起。

隨即，筆者揭開遮蓋在豎式上的卡紙，并肯定了學生的判斷。

將錯例的計算過程先暫時遮掉，讓學生根據結果判斷計算正誤、反推錯誤原因，似乎是故意給學生的思維設置“障礙”，但卻能為課堂提供了更大的探究空間。這樣，不但有助于學生對錯誤的算法印象深刻，也為引導學生經歷從多角度驗證計算的正確性創造了可能，并在探究的過程中使學生的推理能力得到了發展。

三、 不給足夠學具，經歷柳暗花明

由于小學生思維的特點，在小學數學教學過程中，常常要借助直觀學具的幫助。但有時為學生準備“太過充足”的學具反而會阻礙學生思維的發展，并不利于教學目標的實現。在教學《長方形和正方形面積的計算》時，筆者給每個學生準備了7個邊長1厘米的小正方形，用來測量如下6個圖形的面積。（單位：厘米，在給學生的圖形上沒有標出各條邊的長度。）