新型含能材料爆炸驅動能力數值模擬研究

劉天浩，孔德仁，侯景華，姜旻昉，李東岳

(1. 南京理工大學 機械工程學院，江蘇 南京 210094； 2. 中國酒泉衛星發射中心，甘肅 酒泉 735000)

0 引 言

新型含能材料相比于常規的材料體積較小，卻包含了更加巨大的能量. 新型含能材料爆炸產生的爆炸沖擊波具有較強的驅動能力，使破片附帶超高的速度并沿膛口飛出，最直接能表示含能材料對預制破片驅動能力大小的就是破片飛出驅動裝置后的最大速度[1]. 因此，利用AUTODYN進行模擬數值仿真來科學評價含能材料爆炸驅動破片的能力，為破片驅動能力試驗提供數據支持和理論基礎.

目前，國內外學者對爆炸驅動的研究較多. 羅智恒，向永，何碧[2]等人針對研發、 檢測彈藥的安全性試驗需求，通過分析高速破片加載的內彈道特性，結合身管結構的強度分析，設計了一種采用火藥燃氣驅動的高速破片發射裝置，該裝置口徑為25 mm，長度為4 m. 最大裝藥量為200 g，發射最大破片質量為75 g，最大膛壓可以達到250 MPa. 文中計算了速度、 壓力與裝藥量、 破片質量的關系，并與試驗結果進行比較，發現二者具有較好的一致性. 利用該發射裝置，可將65 g質量的破片發射速度達到1 840 m/s，實現了破片的高速可控加速，可應用于彈藥的破片撞擊安全性考核； 李廣嘉，呂永柱[3]等人設計了一種破片高速加載裝置，通過延長身管長度、 加大藥室裝藥量的方法來提高破片速度，并提出采用模擬破片考核破片高速加載裝置，組建了模擬破片速度測量系統，針對3種破片工況分別展開了速度測試實驗. 結果表明，該裝置可以將15 g破片速度加載到2 164 m/s，且破片速度穩定，可以滿足靶場測試需求，驗證了該裝置的實用性和有效性； 楊相禮，何勇[4]等人為獲得更精確的預制破片初速計算模型及破片變形與內襯層破裂半徑對初速的影響規律，利用AUTODYN并采用Johnson-Cook本構模型和流固耦合算法對一種圓柱形預制破片進行了爆炸驅動仿真研究. 仿真結果表明： 預制破片及修正后的鎢合金破片的理論初速與仿真結果吻合較好，驗證了計算模型的正確性.

本文利用非動力學軟件AUTODYN建立了一種專用的爆炸驅動模型進行仿真，利用3種質量(50 g，100 g，200 g)下的3種含能材料(TNT，HMX-TNT，HMX)對同一破片進行爆炸驅動仿真研究. 得到3種含能材料爆炸作用下破片飛行速度時程曲線； 對比分析不同質量同一含能材料爆炸破片速度時程曲線和同一質量下不同含能材料爆炸鎢珠的速度時程曲線； 繪制破片飛行速度，對含能材料質量和含能材料種類的三維曲面進行分析研究； 并計算不同爆炸材料爆炸對鎢珠的最大動量值，最終以最大速度和最大動量為基礎評判上述3類材料的驅動能力大小.

1 爆炸驅動仿真模型總體設計

經過對公開發表的文章中爆炸驅動模型進行參考，對其主要部件及參數按照1∶1進行設計仿真建模，簡化模型如圖1 所示[5].

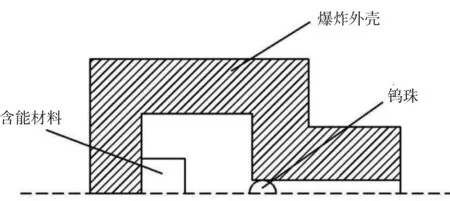
圖1 爆炸驅動仿真模型Fig.1 Explosion-driven simulation model

經過某研究所多年來對含能材料壓裝情況的調研，發現當圓柱型裝藥長徑比大于1.3以后，容易發生壓裝密度不均勻的情況，可能對爆炸驅動破片速度產生干擾，故確定長徑比在1.3以下，本文經過計算將長徑比確定約為1.2左右. 另一方面，從便捷性和安全性角度出發，新型含能材料裝藥量不宜過大，結合現有的壓藥模具并考慮長徑比等進行綜合考慮，確定當量為50 g，100 g，200 g. 各裝藥量長徑如表1 所示.

表1 3種含能材料藥柱長徑表

破片選擇球形Φ8 mm鎢珠，Φ8鎢珠是目前多種戰斗部上應用比較廣泛的球形破片，尺寸結構滿足本次仿真實驗需求并且球形破片在空氣中飛行時迎風面保持不變. 根據鎢珠尺寸，裝藥尺寸等設計破片驅動裝置的仿真模型殼體. 通過加大壁厚來減緩殼體破裂時間，避免爆炸氣體過早泄漏，使更多的爆炸能力作用于加速破片，使仿真結果更加精確可信.

加速管是鎢珠加速的主要階段，根據實際情況和理論研究，設計破片加速管道長度為80 mm，可以適當延長爆炸氣體對破片的加速效果，并且出膛口后含能材料后效力較小，近乎完全爆炸，讓仿真結果更加精確，基本簡化模型如圖2 所示.

圖2 仿真材料模型Fig.2 Simulation material model

模型中空氣為理想氣體狀態，密度為0.001 225 g/cm3，E=4.29*106J/Kg； 裝藥為柱狀含能材料裸裝藥，采用JWL狀態方程[6，7]

式中：P為壓力；V為體積；E為內能；A和B為材料參數；R1，R2和ω為常數. 其中3種含能材料具體參數如表2 所示.

表2 3種含能材料JWL方程基本參數

由于各個模型中材料的不同其對應的要求和求解方式也不同，所以各個部分選擇對應的求解器進行求解. 含能材料爆炸后微粒在空氣域中進行傳播，所以選擇Euler多物質求解器； 為了確保仿真精度和遵循流體網格小于固體網格的要求，選取空氣域網格為1 mm*1 mm，材料通過單元格進行流動； 含能材料，外殼和鎢珠都是固體材料，所以常采用Lagrange求解器進行求解計算. 在一個半密閉的裝置內部放置3種材料，鎢珠在爆炸產生的沖擊波下經過加速管飛出，從而達到驅動破片的目的[8].

2 爆炸驅動數值模擬仿真結果分析

2.1 破片飛行速度仿真結果

本文在仿真實驗上分別設置3種含能材料(TNT，HMX，HMX-TNT)和3種當量(50 g，100 g，200 g)的爆炸驅動破片仿真實驗. 為了更加直觀地研究不同含能材料爆炸驅動能力大小，利用破片速度進行間接表征不同材料的爆炸驅動能力. 在該設置下得到破片不同情況下速度時程曲線如圖3 所示.

(a) 50 g TNT

(b)100 g TNT

(c)200 g TNT

(d)50 g HMX-TNT

(e)100 g HMX-TNT

(f)200 g HMX-TNT

(g)50 g HMX

(h)100 g HMX

(i)200 g HMX圖3 3種含能材料不同當量爆炸驅動破片速度曲線Fig.3 Curves of explosion-driven fragmentation speeds of threeenergetic materials with different equivalents

對上述圖3 中的曲線進行對比分析可以得到： ① 對于同一含能材料不同質量來說，破片最大飛行速度隨著含能材料質量的增加而增大，即破片最大飛行速度與含能材料的質量呈正相關； 破片達到最大飛行速度的時刻隨著含能材料質量的增加而提前，即破片到達最大飛行速度時刻與含能材料質量呈負相關. ② 對于同一質量不同含能材料來說，破片最大飛行速度受含能材料的影響較大. 具體表現為： 當含能材料由TNT到HMX-TNT(1∶1)到HMX變化的過程中，破片飛行速度曲線加速階段更加陡峭，破片飛行最大速度也逐漸增大. 雖然不同材料爆炸驅動得到的破片速度各個階段都存在差異，但速度曲線總體保持一致. ③ 隨著驅動材料質量的增加，破片最大速度增長率也隨之增長，可近似地認為破片最大飛行速度增長率和驅動材料質量成正相關.

2.2 不同含能材料驅動能力對比

由于上述曲線只能表示特定材料、 特定當量下的破片最大飛行速度狀態，所以無法從整體的結構上分析材料、 裝藥質量大小對破片飛行速度的影響情況，將上述曲線中的數據進行提取，繪制成如圖4 所示的破片最大飛行速度與裝藥質量和驅動材料之間的3位曲面.

對圖4 曲面進行分析可以發現： ① 當TNT當量為50 g時，破片最大速度達到286.56 m/s； 當TNT當量為100 g時，破片最大速度達到468.87 m/s； 當TNT當量為200 g時，破片最大速度達到588.87 m/s； TNT當量由50 g～100 g過程中，破片最大飛行速度變化率為3.646 2 m/s每克TNT，TNT當量由100 g～200 g過程中，破片最大飛行速度變化率為1.2 m/s每克TNT. ② 當HMX-TNT當量為50 g時，破片最大速度達到326.29 m/s； 當HMX-TNT當量為100 g時，破片最大速度達到525 m/s； 當HMX-TNT當量為200 g時，破片最大速度達到655.78 m/s； HMX-TNT當量由50 g～100 g 過程中，破片最大飛行速度變化率為3.974 2 m/s 每克HMX-TNT； HMX-TNT當量由100 g～200 g過程中，破片最大飛行速度變化率為1.307 8 m/s每克HMX-TNT. ③ 當HMX當量為50 g時，破片最大速度達到329.43 m/s； 當HMX當量為100 g時，破片最大速度達到483.72 m/s； 當HMX當量為200 g時，破片最大速度達到777.35 m/s； HMX當量由50 g～100 g過程中，破片最大飛行速度變化率為3.085 8 m/s每克HMX； HMX當量由100 g～200 g過程中，破片最大飛行速度變化率為2.936 3 m/s每克HMX. 綜合3同含能材料進行仿真實驗得到的結果可以看出，在同一環境、 同一狀態和同一質量的3同原則前題下，隨著含能材料當量的增加，其對破片最大飛行速度的影響逐漸減弱. ④ 圖4 曲面從橫向來看，TNT，HMX-TNT，HMX 3種含能材料爆炸驅動破片得到的最大速度HMX最大，HMX-TNT混合材料其次，最后是TNT； 從縱向來看，同一含能材料隨著質量不斷增加，得到的驅動破片最大速度也不斷增加，驅動能力也隨之增加.

圖4 破片飛行最大速度曲面Fig.4 Surface of the maximum speed of fragment flight

2.3 不同含能材料驅動能力表征

綜上所述，HMX，HMX-TNT，TNT 3種材料爆炸驅動破片得到的速度大小各不相同，總體對3種爆炸材料爆炸驅動破片得到的最大速度趨勢是： HMX>HMX-TNT>TNT； 但隨著鎢珠質量大小的變化，破片最大飛行速度也會隨之變化，所以需要尋求一種表征量，使得能對不同種爆炸材料的驅動能力和速度與驅動破片的質量相關聯，因此本文在對爆炸材料的驅動能力表征上選用動量，計算不同材料驅動破片最大速度與破片質量的乘積結果來表征爆炸材料的驅動能力，動量計算公式為

I=mv,

式中：m為破片的質量；v為破片最大速度.

3種爆炸材料不同質量下最大動量如圖5 所示.

圖5 不同驅動材料不同質量下破片最大動量曲面Fig.5 Maximum momentum surface of fragment underdifferent driving materials and different masses

圖5 曲面在一定程度上可以得到不同爆炸驅動材料的驅動能力與材料的類型和質量之間的關系，但無法定量進行分析，所以對圖5 曲面中的數據進行提取，如表3 所示.

表3 3種含能材料下破片最大沖量

對表3 進行分析可得： TNT，HMX-TNT，HMX 3種含能爆炸材料在保持裝藥質量一定的情況下，HMX的動量數值最大，HMX-TNT其次，TNT最小. 在同一材料，不同裝藥質量的情況下，破片最大動量隨裝藥質量的增加而增大，所以破片最大動量與裝藥質量成正比. 對于上述3種驅動材料，綜合考慮裝藥質量和爆炸材料種類，可以得出3種爆炸材料對于破片驅動能力大小由高到低分別為HMX> HMX-TNT>TNT[9，10].

3 結 論

本文利用AUTODYN軟件對不同當量TNT，HMX-TNT，HMX爆炸驅動破片進行數值仿真，獲取了爆炸驅動破片的速度數據，對其進行分析得到：

1) 同種含能材料，隨著TNT，HMX-TNT，HMX當量的增加，爆炸驅動破片能力逐漸增強，并且破片飛行最大速度，最大動量與含能材料裝藥當量成正相關，加速到最大速度所需要的時間，加速度達到最大的時間和裝藥當量成負相關.

2) 3種含能材料爆炸驅動破片得到的最大速度規律依次為： HMX>HMX-TNT>TNT； 破片最大動量規律依次為HMX>HMX-TNT>TNT； 綜合上述可以得到3種含能材料爆炸驅動能力大小依次是： HMX>HMX-TNT>TNT；

3) 本文通過AUTODYN建立爆炸驅動裝置模型，對不同當量的TNT進行爆炸驅動破片模擬仿真研究，可以為今后實際爆炸驅動試驗提供一定的數據支撐和理論依據，對爆炸材料驅動能力的研究具有重要的指導意義，使今后爆炸驅動裝置的設計和相關實驗研究有一個整體的宏觀認識.