半變系數模型中參數的幾乎無偏Liu估計

（華北水利水電大學 數學與統計學院，河南 鄭州450046）

一、引言

本文考慮如下半變系數模型[1]：

其中，（Yi，Xi1，Xi2，…，Xim，Ui）（i=1，2，…，n）是因變量 Y和自變量 X1，X2，…，Xm，U 的第 i個樣本觀測值，U為時間或空間變量，假設βj（U）為自變量U的一元光滑函數；βj為常值系數，ε為誤差項，且滿足E（εi|Ui，Xi1，Xi2，…，Xim）=0，Var（εi|Ui，Xi1，Xi2，…，Xim）=σ2（i=1，2，…，n）。半變系數模型是一類比較廣泛的模型，如果將常值系數βj看作函數，半變系數模型可以認為是變系數模型的特殊情況；當X1=1，q=1時，就轉化為部分線性模型。目前半變系數模型已經獲得了廣泛的研究和應用[2][3][4]。眾多學者得到該模型參數的估計方法，比如：兩步估計法、小波估計法、一般級數法等[5][6][7][8]；針對模型中常系數的估計問題，Fan Jianqing和Huang Tao基于局部線性擬合方法提出常系數的輪廓最小二乘估計[9]，魏傳華和吳喜之在模型附加有線性約束條件時提出了約束輪廓最小二乘估計[10]，孫倩和韋杰在具有隨機約束時提出參數分量的輪廓混合估計[11]等。當設計矩陣存在復共線性，劉超和韋杰等進一步提出了參數分量的輪廓混合嶺估計[12]；Trenkler G，Toutenburg H提出幾乎無偏嶺估計[13]。作為對上述工作的深入，本文在輪廓最小二乘估計的基礎上提出半變系數模型中參數的Liu估計以及幾乎無偏Liu估計，并研究了相關性質。

二、估計的提出

三、幾乎無偏Liu估計的優良性

四、數值模擬

采用文獻[15]中的數值模擬方法，令

其中解釋變量x1與x2由

xij=（1-ρ2）1/2zij+zip，（0＜ρ＜1），i=1，2，…n，j=1，2，…p生成，ρ是給定的常數，ρ2表示兩個不同解釋變量之間的相關性，zij、εi、xi3分別是服從 N（0，1）、N（0，σ）2、均勻分布 U[-1，1]的隨機數。取n=50，150，200，ρ=0.80，0.90，0.95，0.99，σ2=0.1，根據交叉確認法可得 h=0.1025，0.0851，0.1256， 記 PLSE、RE、AURE、LE、AULE為參數的輪廓最小二乘估計、嶺估計、幾乎無偏嶺估計、Liu估計、幾乎無偏Liu估計的均方誤差，得模擬結果如下：

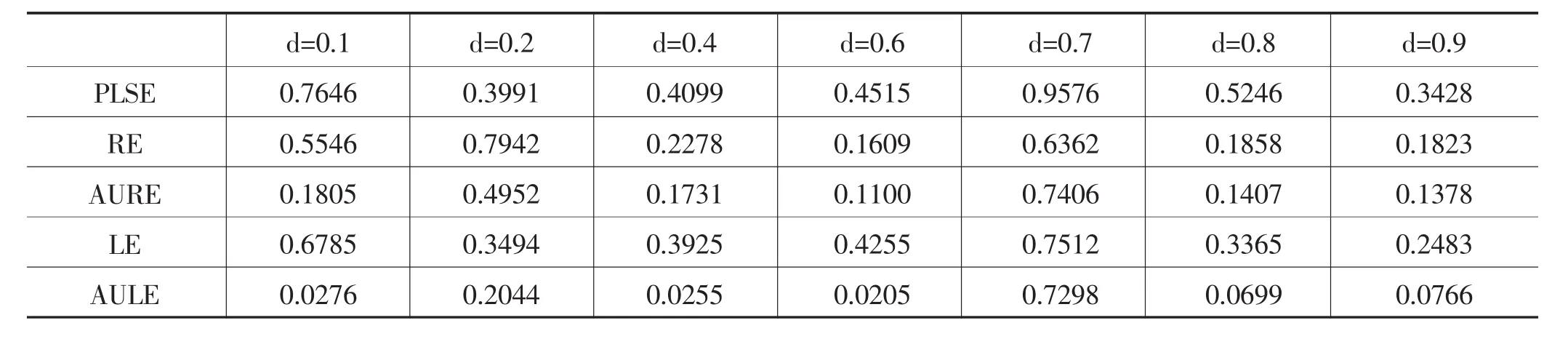
表1 五種估計的均方誤差模擬結果（n=50，h=0.1025，ρ=0.80，k=1.2591）

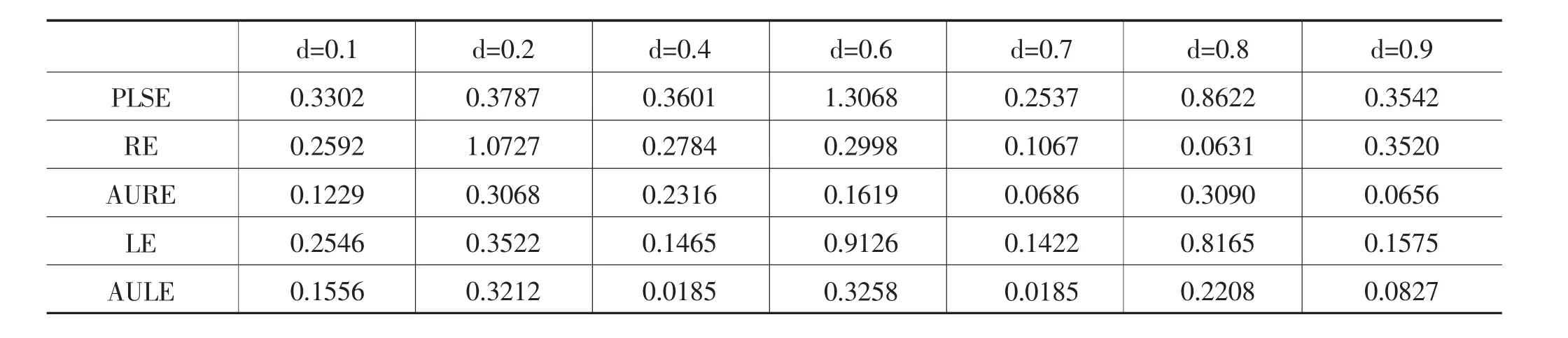
表2 五種估計的均方誤差模擬結果（n=50，h=0.1025，ρ=0.90，k=1.2578）

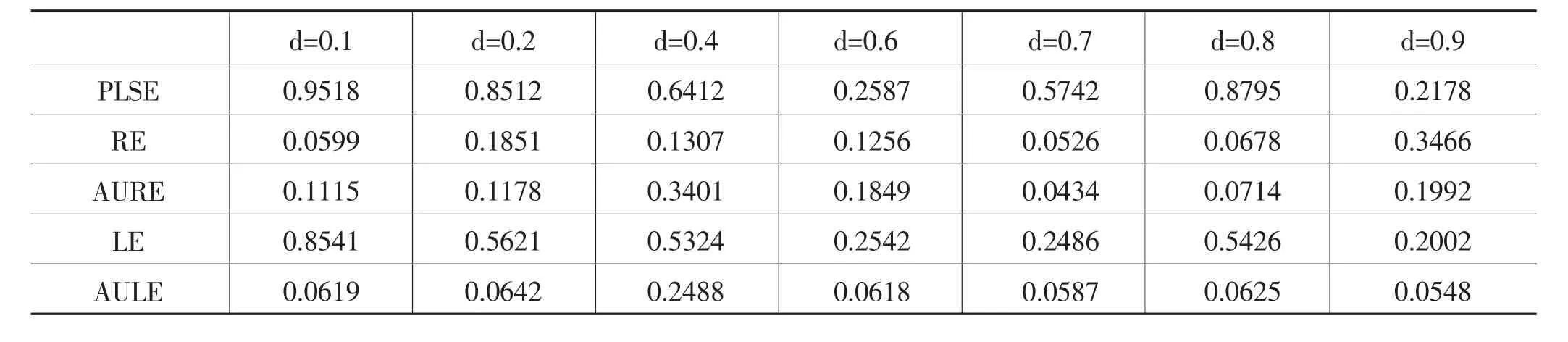
表3 五種估計的均方誤差模擬結果（n=150，h=0.0851，ρ=0.90，k=1.2574）

表4 五種估計的均方誤差模擬結果（n=150，h=0.0851，ρ=0.95，k=1.3148）

表5 五種估計的均方誤差模擬結果（n=200，h=0.1256，ρ=0.95，k=1.3265）

表6 五種估計的均方誤差模擬結果（n=200，h=0.1256，ρ=0.99，k=1.3435）

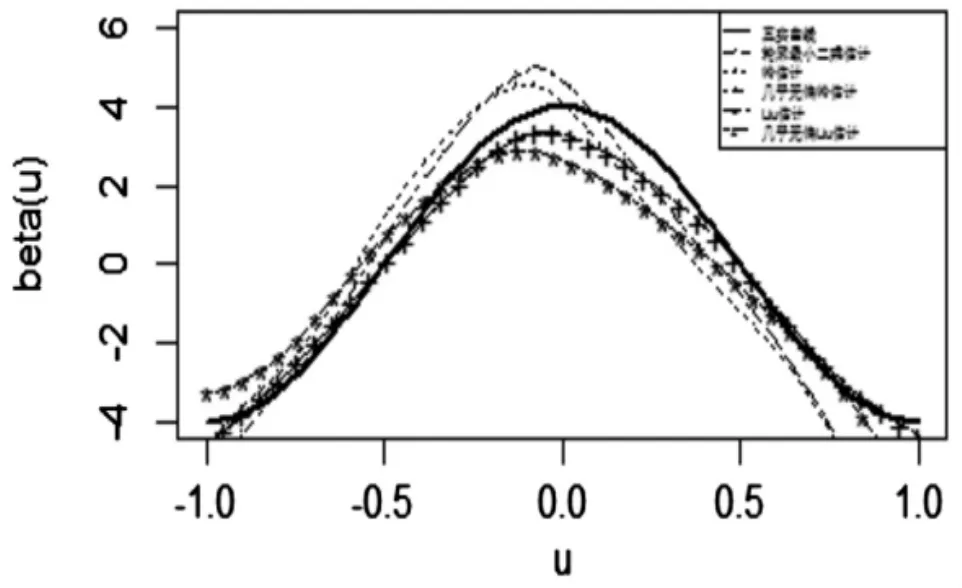
附圖 模型中變系數β（u）=4cos（πu）的擬合圖

五、結語

針對半變系數模型中存在的復共線性問題，本文提出了半變系數模型中參數的Liu估計以及幾乎無偏Liu估計，并且提出了均方誤差準則下幾乎無偏Liu估計優于輪廓最小二乘估計、嶺估計、Liu估計的充分條件，在均方誤差陣準則下幾乎無偏Liu估計優于幾乎無偏嶺估計的充要條件，最后通過數值模擬驗證了相關理論結果。關于變系數Liu估計，幾乎無偏Liu估計的優良性質本文僅從數值模擬進行了驗證，其理論性質將另文探討。