自適應模糊控制在抑制海上漂浮式風力機振動響應中的應用

楊佳佳, 賀爾銘, 舒俊成

(西北工業大學 航空學院, 陜西 西安 710072)

海上風能具有風速高和風切變小等優勢，已成為最具開發價值的綠色能源之一[1]。作為遠深海風能利用的重要載體，海上漂浮式風力機是一個復雜的風浪擾動-葉片槳距控制器-結構耦合的非線性系統。在隨機風浪作用下，浮動平臺、塔架和葉片等結構將產生巨大的振動響應，嚴重影響海上漂浮式風力機的結構可靠性。因此，采用不同控制方式提高海上漂浮式風力機的抗風浪干擾能力，抑制結構的振動響應，已成為當前海上漂浮式風力機研究的重要課題。

被動控制策略是提高海上漂浮式風力機抗風浪干擾能力的一種有效途徑。2011年，Lackner等[2]首次利用質量調諧阻尼器(TMD)系統降低隨機風浪對風力機振動的影響，并將機艙TMD模塊集成到風力機振動特性分析軟件FAST中。隨后，Jin、He等[3-4]采用改進的人工魚群算法(AFSA)優化了風力機TMD參數，結果表明，最優TMD能夠顯著降低風力機的塔頂前后(TTFA)撓度。2020年，Zhang[5]建立了旋轉葉片-TMD的2-自由度(2-DOF)動力學模型，根據頻率調諧公式，得到TMD的最優阻尼比，發現TMD的最優阻尼比取決于葉輪的旋轉速度。Jahangiri等[6]采用三維擺調諧質量阻尼器(3D-PTMD)和雙線性沖擊調諧質量阻尼器(2PTMDs)減小Spar式風力機在風浪荷載作用下的三維振動，結果證明，二者均能有效降低風力機的振動響應，且2PTMDs的行程約為3D-PTMD的50%。

近幾年，采用主動控制策略減小風力機結構振動逐漸成為一個研究熱點。Horacio等[7]基于主動干擾抑制(ADR)的控制方式減小風力機的變頻周期性負荷擾動，發現和被動控制相比，ADR可以進一步降低周期性負荷擾動對風力機結構振動的影響。Jaime等[8]設計了一種基于葉尖撓度測量和單槳距控制的新型葉片槳距主動控制器，仿真結果證明，新型主動控制器可以降低葉輪關鍵部件的疲勞損傷。Fitzgerald等[9]結合漂浮式風力機的結構動力學模型和概率評估工具，研究了主動調諧質量阻尼器(ATMD)對風力機塔架可靠性的影響，分析發現，在額定風速下，ATMD在一定程度上改善了塔架的可靠性。

2015年以來，本課題組[10-12]基于拉格朗日能量法建立了Barge式風力機的結構動力學模型，并分別在機艙和平臺中配置TMD，結果表明，機艙TMD和平臺TMD均可有效提高結構的抗風浪干擾能力。另外，課題組研究了線性二次型調節器(LQR)對Barge式風力機振動響應的影響，發現和機艙TMD系統相比，LQR控制器的減振效果可提升20%左右[13-14]。

常規最優控制策略，如LQR控制、H控制等依賴于精確的動力學模型。海上漂浮式風力機是一個復雜的剛-柔耦合非線性系統，在隨機風浪引起的風力機振動平衡位置變化、葉片槳距控制器耦合效應導致的結構參數攝動、惡劣的海洋環境引起的結構腐蝕和疲勞損傷等多因素作用下，風力機動態特性難以掌握，建立精確的動力學模型非常困難。此時，采用常規最優控制策略減小隨機風浪對風力機結構振動的影響是不可行的。模糊控制具有不依賴于精確的動力學模型、魯棒性好、抗干擾能力強等優點。因此，有必要在隨機風浪擾動和葉片槳距控制器耦合作用下，進一步研究模糊控制策略對海上漂浮式風力機結構振動的影響。本文以美國NREL實驗室開發的Spar型漂浮式風力機模型為基礎，設計開發了自適應模糊控制器，在隨機風浪擾動和葉片槳距控制器耦合作用下，研究了不同控制策略對Spar風力機結構振動的控制效果。

1 Spar式風力機剛-柔耦合非線性動力學模型

Spar式風力機剛-柔耦合結構簡圖見圖1a)，平臺為剛體，塔架和葉片為柔性體，機艙為固定于塔頂的質點。風力機浮式平臺通過錨線系統和海床相連，錨線系統簡化為平臺對應DOF的彈簧，隨機風浪沿X軸作用于葉輪和浮式平臺。OXYZ為慣性坐標系,OXY平面與靜水面平行,Z軸豎直向上。ohijk為固定于葉輪上的旋轉坐標系,原點o固定于輪轂,i軸沿葉片1長度方向,j軸在旋轉平面內垂直于i軸,k軸垂直于ohij平面。Spar式風力機的基本參數見表1。

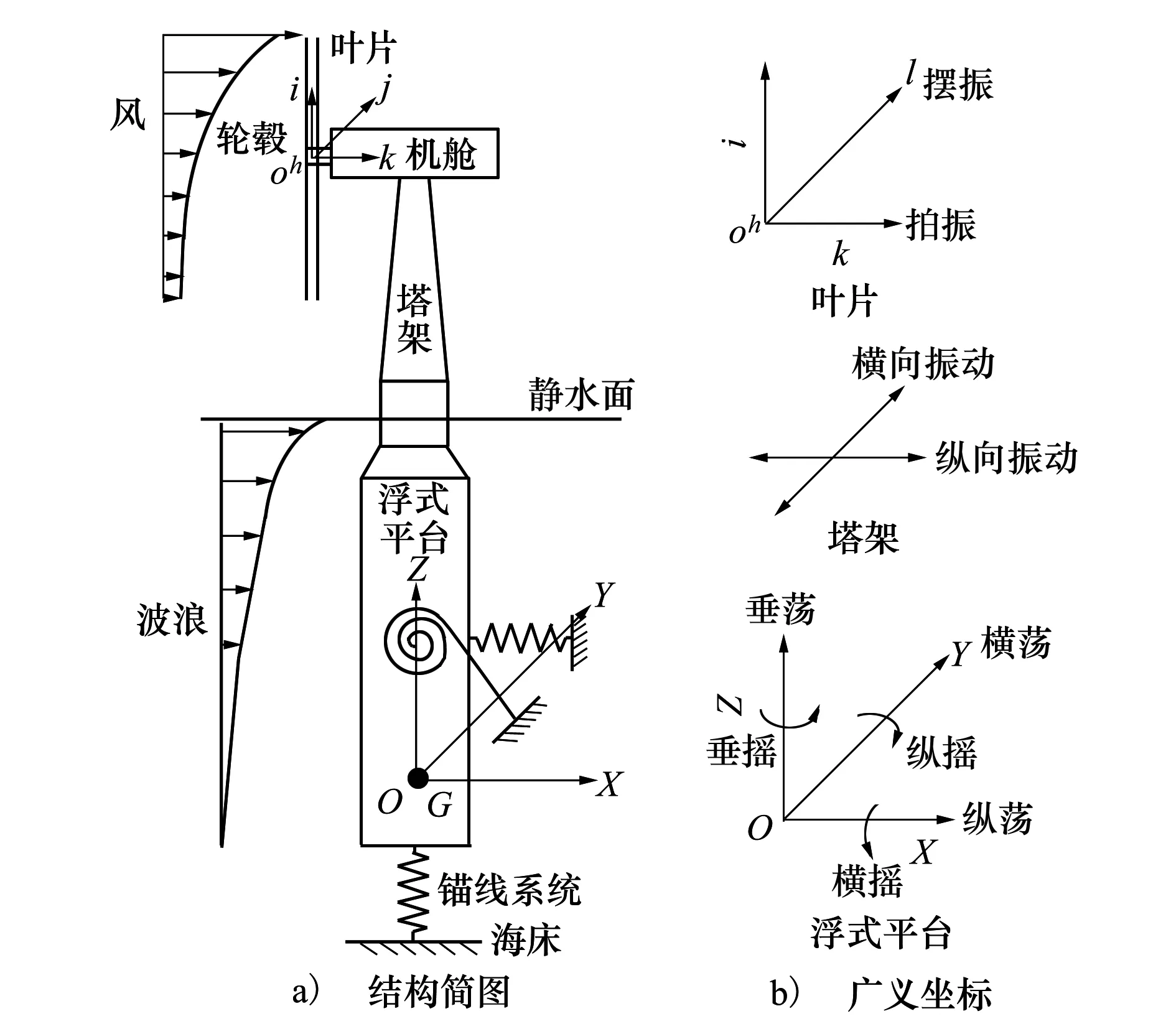
圖1 Spar式風力機結構簡圖和DOF

表1 Spar式風力機的基本參數

在浮式平臺和機艙分別安裝TMD系統,如圖2所示。Mp和Mn分別為平臺/機艙TMD的質量塊,則TMD系統由質量m、剛度系數k和阻尼系數c組成。另外,在機艙中安裝主動作動器fTn,對Mn施加主動控制力u,即可構成混合質量阻尼器(HMD)系統。

圖2 平臺/機艙TMD系統示意圖

最優TMD參數如表2所示。

表2 最優TMD參數

設Spar式風力機的廣義坐標向量q為

(1)

式中：上標p,t,b,T分別表示平臺、塔架、葉片和TMD，上標ba分別代表3個葉片(a=1,2,3)；Tp,Tn表示平臺TMD和機艙TMD,下標為對應廣義坐標的縮寫,詳見圖1b),本文假定q完全可測。

那么,Spar式風力機剛-柔耦合非線性動力學模型可記為

(2)

式中：f(·)和g(·)為未知有界的非線性函數；f(·)代表風力機的結構參數；g(·)表示控制力的位置矩陣;fd為隨機風浪擾動及結構參數攝動。

通過文獻[14]的研究發現,抑制PFPI運動不僅可以降低風力機平臺的振動響應,還可減小TTFA的低頻振動,因此,PFPI運動是表征風力機振動響應的一個關鍵參數。本文將PFPI作為控制對象,通過計算PFPI運動和目標值之間的誤差與誤差變化率實現模糊控制。

2 傳統模糊控制器設計

圖3 模糊控制系統

模糊規則是模糊控制器的核心,其基本形式如下

如果e=E且ec=EC,則u=U

(3)

式中,E，EC，U分別代表e，ec和u的模糊子集。

模糊規則直接影響模糊控制效果的優劣,為了減小設計者主觀經驗對模糊規則的影響,針對Spar式風力機復雜的工作環境,在文獻[14]中所推導的線性數學模型基礎上,以PFPI標準差最小為優化目標,引入2個修正因子,優選出相應的模糊規則。具體過程為:

1) 將e,ec和u的論域劃分為7個模糊子集,分別用-3(負大)、-2(負中)、-1(負小)、0(零)、1(正小)、2(正中)、3(正大)表示。

2) 引入修正因子,利用公式(4),得到多個輸出模糊子集。

(4)

式中,α1，α2表示修正因子,取值范圍為[0,1];〈·〉表示四舍五入取整。

3) 將不同的模糊子集嵌入圖3b)中,結合文獻[14]給出的數學模型,計算PFPI標準差。

圖4為工況1和工況3的PFPI標準差隨α1，α2變化規律。可以看出,工況1中,α1和α2分別取0.5,0.6時,標準差最小;工況3中,α1，α2分別取0.5，0.4時,PFPI的標準差最小。

圖4 PFPI標準差隨α1，α2的變化規律

使用乘積推理機、單值模糊器和中心平均解模糊器,得到FC為

(5)

式中：y為模糊規則中U對應的模糊數；θ表示49條模糊規則中U對應的模糊數組成的向量,共包含49個元素;l1,l2分別表示E和EC模糊子集的編號；l1=l2=1,2,…7;x1和x2代表e和ec的取值;μ為x1和x2對應的隸屬度,隸屬度采用高斯隸屬函數計算;ξ(q)是一個含有49個元素的列向量,表示每條模糊規則輸入值的隸屬度之積除以49條規則的隸屬度之積的和。

3 自適應模糊控制器設計

假設傳統模糊控制器的參數θ可調,則傳統模糊控制器進化為自適應模糊控制器。因此,本節主要根據Lyapunov第二方法設計自適應模糊控制器。

根據文獻[15],誤差狀態方程可寫為

(6)

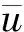
(7)

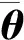
選擇Lyapunov函數

(8)

式中,P正定且滿足Lyapunov方程(9);rθ為正常數。

ΛTP+ΛP=-Q

(9)

式中,Q為正定矩陣。

對V求導可得

(10)

(11)

由此可得AFC為

(12)

4 自適應模糊控制器有效性驗證

本節采用2種方法驗證AFC的有效性：

1) 給定方波作為目標值，研究FC和AFC作用下PFPI的跟蹤效果；

2) 結構存在參數攝動fd時，研究FC和AFC作用下PFPI對方波的跟蹤效果。

圖5a)為目標值變化時，FC與AFC對目標值的跟蹤圖，明顯的，AFC能夠更好更快地跟蹤目標值。圖5b)為跟蹤誤差，由于目標值突變，導致跟蹤誤差出現尖峰；方波幅值為2時，FC的最小跟蹤誤差為0.124 3，AFC的最小跟蹤誤差為0.043 5。圖5c)為控制力輸出，可知，當跟蹤誤差出現尖峰時，需要一個更大的控制力使峰值快速下降，此時，AFC的控制力輸出約為FC的1.89倍；當跟蹤誤差趨近于0時，控制力逐漸平緩。

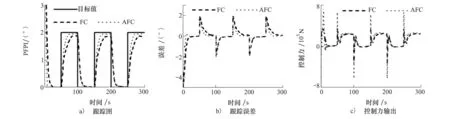
圖5 PFPI跟蹤效果

圖6為結構存在參數攝動fd=3.6×108×sin(1.047 1t)時，PFPI對目標值的跟蹤效果。由于存在參數攝動，前30 s的跟蹤誤差和控制力輸出存在較大波動，隨后達到一個相對平穩的跟蹤過程。FC最小跟蹤誤差為0.126，AFC跟蹤誤差為0.055；AFC控制力輸出峰值為FC峰值的1.92倍。

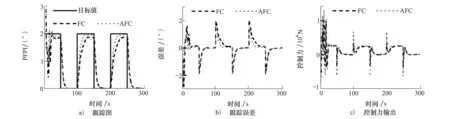
圖6 參數攝動時PFPI跟蹤效果

由圖5和圖6可知，AFC對目標值的跟蹤能力明顯優于FC，因此，所設計的AFC是有效可行的。

5 基于模糊控制的海上漂浮式風力機振動抑制研究

湍流風的風速和風壓相對于時間是隨機變化的，波浪的波高、波長、方向、位相是由不同頻率的隨機波疊加而成的，導致很難準確預測海上風浪工況。如果用輪轂處風速代替作用于風力機的湍流風，將波長和位相作為隨機變量，那么可用隨機過程理論反映海上波浪的隨機特性。根據海上風力機設計標準IEC-3的規定，風速譜選擇Kaimal譜，波浪譜采用Pierson-Moskowitz譜，海上漂浮式風力機常用的風浪工況基本參數見表3。

表3 風浪工況基本參數

通過6次300 s的海上風浪模擬，取其平均值，則海上風浪時程曲線見圖7。可以看出，風浪具有很強的隨機性。工況1風速較低，均值約為8 m/s，波高峰值約為1.47 m；工況3平均風速約為18 m/s；波高峰值約為2.84 m。

圖7 海上風浪時程曲線

圖8為隨機風浪作用下，葉片槳距角的時程曲線。由圖可知，工況1的風速較低，葉片槳距控制系統停止工作，槳距角維持為0；工況2的槳距角變化范圍為0°～ 10°；工況3和工況4的風速超出額定值，槳距角隨風速的改變而變化，且風速越大，槳距角越大。

圖8 葉片槳距角變化時程曲線

圖9為在隨機風浪擾動和葉片槳距控制系統耦合作用下，不同控制方式的PFPI運動PSD圖。明顯的，FC和AFC的PSD峰值遠遠低于TMD被動控制的峰值，且PSD能量主要集中在0～0.15 Hz內。和被動控制相比，工況1中，FC和AFC對PFPI運動的PSD峰值的抑制效果為34.24%,38.97%，工況3中，2種模糊控制作用的PSD峰值分別減小了35.95%,39.06%。

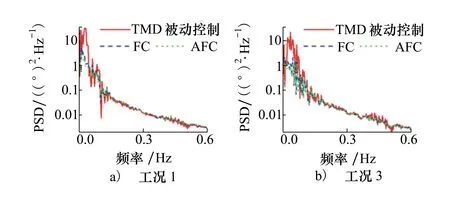
圖9 不同工況的PFPI運動PSD

圖10為FC和AFC的控制力PSD圖。同樣的，控制力能量主要集中在0～0.15 Hz內；不同工況下，AFC的控制力峰值約為FC峰值的1.1倍。

圖10 不同工況的控制力PSD

表4為時域中不同模糊控制方式對隨機風浪擾動的抑制能力，均值代表控制后平衡位置接近目標位置的程度，標準差反映振動響應的波動程度。AFC的均值抑制率小于FC，表明AFC作用下，PFPI及TTFA更接近于TMD被動控制的均值(目標位置)；AFC的標準差抑制率高于FC，則AFC對PFPI運動和TTFA撓度的抑制能力更強。

表4 時域中不同控制方式抑制風浪擾動的能力

6 結 論

本文基于Lyapunov第二方法設計了自適應模糊控制器，并研究了不同模糊控制策略抑制風力機振動響應的能力。主要結論如下：

1) 相比于傳統模糊控制器，所設計的自適應模糊控制器能夠更好更快地跟蹤目標值；跟蹤誤差出現尖峰時，控制力輸出達到最大。

2) 結構存在參數攝動時，前30 s的跟蹤誤差和控制力輸出存在較大波動，隨后的跟蹤過程相對平穩。

3) 葉片槳距控制器耦合作用下，相對于TMD被動控制策略，自適應模糊控制器對平臺俯仰運動的PSD峰值的最大抑制效果為39%左右。

4) 不同工況下，自適應模糊控制器的控制力峰值約為傳統模糊控制器峰值的1.1倍，且控制力能量主要集中在0～0.15 Hz內。