基于威脅建模的UCAV武器投放在線航跡規(guī)劃

唐嘉鈺, 李相民, 代進進

(1. 海軍航空大學, 山東 煙臺 264001; 2.海軍研究院, 北京 100422)

攻擊型無人機(unmanned combat aerial vehicle,UCAV)是快速形成對敵威脅、打贏信息化條件下非對稱戰(zhàn)爭的重要手段[1]。UCAV可攜帶小型或大威力的精確制導武器(包括反輻射導彈、紅外制導導彈及制導炸彈等) ，可遂行防空壓制、對地攻擊等作戰(zhàn)任務[2]。

航跡規(guī)劃技術是成功實現(xiàn)UCAV自主攻擊的關鍵技術之一[3]。目前無人機航跡規(guī)劃方法主要有Voronoi圖算法[4-6]、A*算法[7-8]、稀疏A*(sparse A*search,SAS)算法[9]、人工勢場法[10-12]、灰狼算法[13-14]和隨機搜索樹(rapid-exploration random tree,RRT)算法[15-16]，在線航跡規(guī)劃則主要通過滾動時域控制獲取實時動態(tài)飛行軌跡[17-20]。目前UCAV航跡規(guī)劃研究主要集中于局部威脅信息已知的靜態(tài)任務場景，未考慮復雜戰(zhàn)場環(huán)境動態(tài)變化(例如突發(fā)威脅和機動目標等)。

針對這一問題，本文提出了基于任務區(qū)域威脅建模的UCAV在線投放航跡規(guī)劃方法。首先，針對UCAV對地攻擊任務需求，將預先求解的機載制導炸彈可投放區(qū)中心和投放姿態(tài)作為終端約束條件，同時考慮飛行器性能和戰(zhàn)場環(huán)境等約束，建立了UCAV武器投放航跡規(guī)劃模型；基于戰(zhàn)場環(huán)境威脅建模，結合模型預測控制的滾動優(yōu)化策略，UCAV通過不斷在線預測判斷飛行態(tài)勢實現(xiàn)自主避障飛行。仿真結果表明，本文所提算法能夠實現(xiàn)UCAV在動態(tài)戰(zhàn)場環(huán)境下在線航跡規(guī)劃。

1 UCAV武器投放航跡規(guī)劃數(shù)學模型

1.1 UCAV運動學及動力學模型

與旋翼飛機相比，固定翼無人作戰(zhàn)飛機具有續(xù)航能力強、飛行速度快及可靠性較高等優(yōu)點，更適合應對復雜動態(tài)多變的戰(zhàn)場環(huán)境。

UCAV在地理坐標系下的質點運動學和動力學方程組分別為

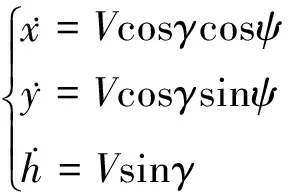
(1)

(2)

(3)

式中:δ為UCAV油門位置;Tmax為UCAV最大可用推力;ρ為空氣密度;S為飛行器橫截面積;CD和CL分別為阻力和升力系數(shù)。

1.2 UCAV機載武器可投放區(qū)模型

為保證機載武器命中精度、提升攻擊效果,UCAV投放制導炸彈時存在特定的區(qū)域限制,這個區(qū)域即為可投放區(qū)。當UCAV在此空域內且滿足投放速度姿態(tài)等約束條件時投放制導炸彈,制導炸彈將以給定精度命中目標,而在此區(qū)域外進行投放時,則無法保證有效地命中目標。因此,UCAV在航跡規(guī)劃前應依據(jù)目標類型和毀傷特性等要素,解算出制導炸彈的可投放區(qū),以此作為航跡規(guī)劃的末端約束條件,確保UCAV完成攻擊前的占位。

1.2.1 制導炸彈運動學模型

1) 制導炸彈彈道模型

計算制導炸彈可投放區(qū)的本質是生成炸彈彈道航跡,為提高計算效率,本文采用三自由度質點運動模型,同時為了便于模型的建立與求解,做以下假設:

(1) 不考慮外界環(huán)境因素對炸彈彈道航跡的干擾,飛行條件設定為標準大氣環(huán)境;

(2) 忽略炸彈彈體的轉動慣性,不研究炸彈在飛行過程中繞質點轉動的情況;

(3) 彈上測量和控制系統(tǒng)能夠準確、理想無延遲工作。

制導炸彈彈體運動學方程與(1)式相同,其動力學方程則為

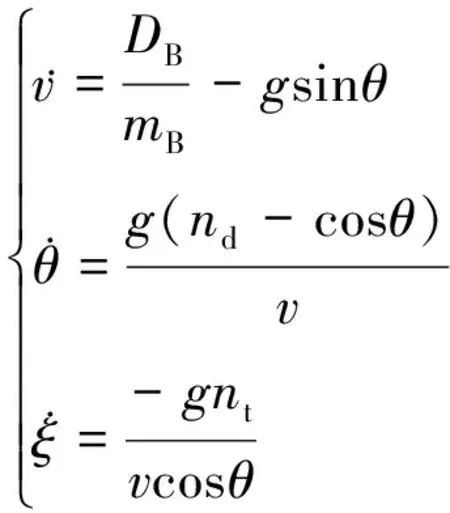
(4)

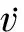
2) 制導律模型

UCAV機載制導炸彈采用比例導引律,不考慮滾轉角及滾轉角速率影響,可將制導炸彈在三維空間上的運動解耦成俯沖和轉彎2個平面上的運動。

制導炸彈視線角速率為

(5)

式中:(lm,pm,sm)表示投放后制導炸彈位置,其中l(wèi)m代表縱向射程;pm代表側向射程;(lT,pT,sT)代表目標點位置;qd和qt分別為視線在俯沖平面內的高低角和轉彎平面內的方位角,則為制導炸彈與目標相對距離

(6)

考慮制導炸彈采用傳統(tǒng)比例導引律,則有

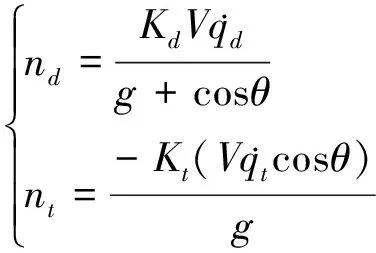
(7)

式中,Kd和Kt為比例導引律的增益。

1.2.2 制導炸彈可投放區(qū)模型

可投放區(qū)模型的求解主要包括兩方面內容:通過計算極限射程彈道獲得制導炸彈可達域;將可達域變換得到可投放區(qū)邊界。可投放區(qū)求解流程如圖1所示。

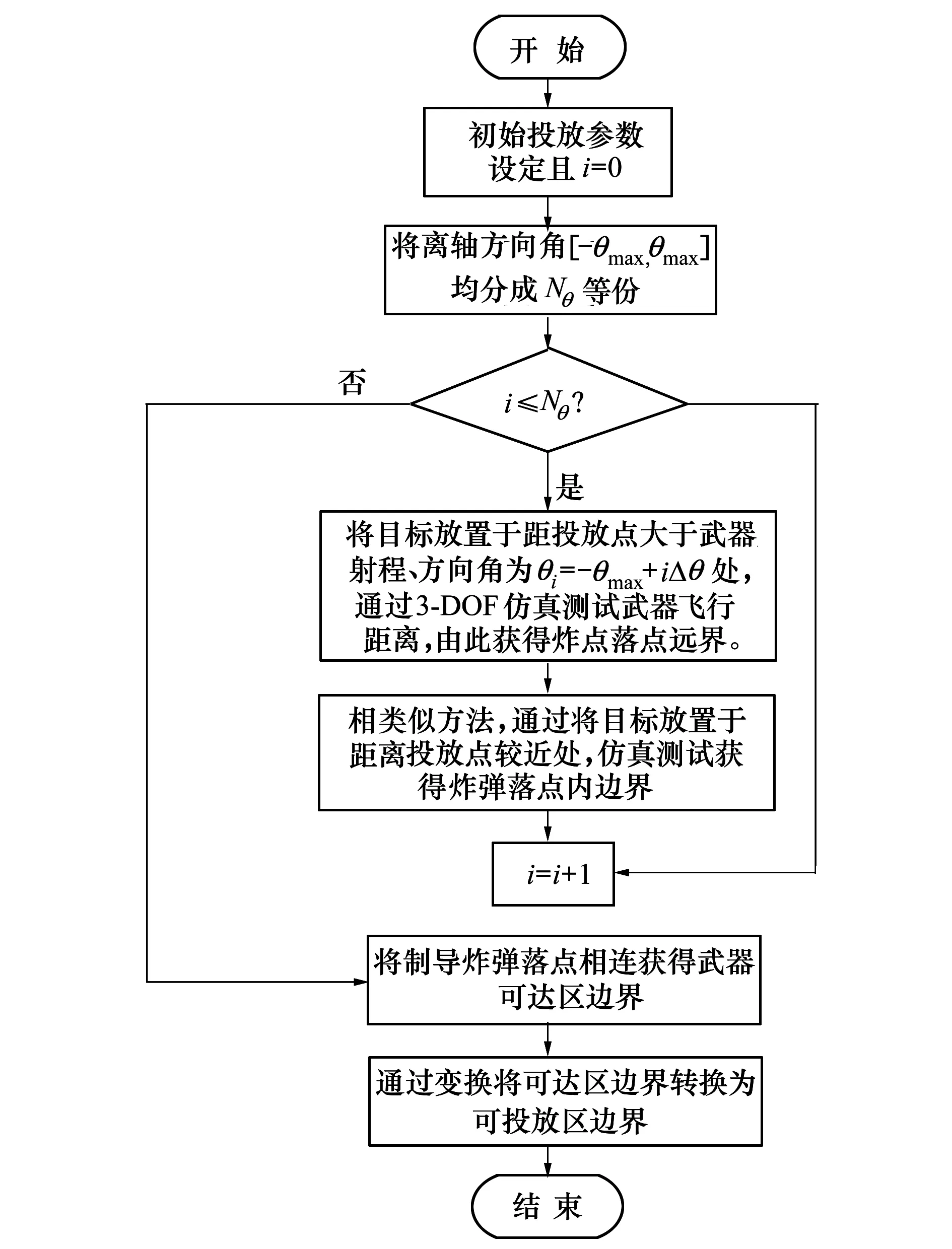
圖1 機載制導炸彈可投放區(qū)包絡求解流程

1.3 UCAV武器投放航跡規(guī)劃約束條件

UCAV武器投放航跡規(guī)劃時需滿足邊值和過程約束兩類約束條件。

1.3.1 邊值約束條件

邊值約束條件主要包括初值約束和終端約束。

1) 初值約束

設任務起始時刻為ts,則初值約束為

(8)

2) 終端約束

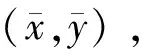
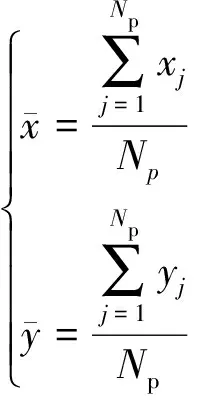
(9)

式中:(xj,yj)為第j個可投放區(qū)包絡頂點;Np為包絡頂點個數(shù)。因此UCAV投放航跡終端約束為

(10)

式中:ε為地理坐標系下所允許的距離偏差;xf,yf及hf分別為UCAV航跡末端點位置。

此外,在武器投放點UCAV還需要滿足一定的速度和姿態(tài)約束,即

(11)

式中:tf為終端時刻；Vrelease為武器投放速度；γrelease為投放航跡傾角；αrelease為投放迎角；ψrelease為投放滾轉角。

1.3.2 過程約束條件

飛行過程中,UCAV需滿足機動性能約束和戰(zhàn)場環(huán)境約束。

1) 機動性能約束

機動性能約束條件主要包括航跡控制量、速度、加速度、航向角及最小轉彎半徑等約束。根據(jù)UCAV機動性能,具體建立如下過程約束條件

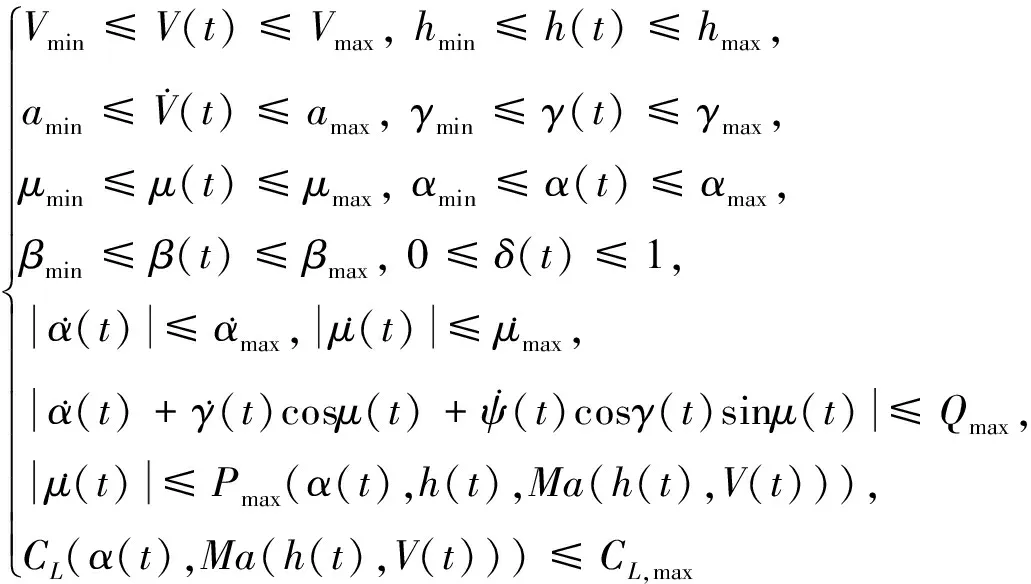
(12)

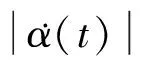
2) 戰(zhàn)場環(huán)境約束

UCAV在對地攻擊過程中會碰到地形障礙及防空陣地等安全威脅。飛行過程中UCAV應盡可能避開這些威脅,同時與目標保持一定距離以保證自身安全。

戰(zhàn)場環(huán)境約束條件主要分為硬威脅和軟威脅2類。硬威脅是指無人機無法進入的障礙區(qū)域,例如山體、建筑物及其他禁飛區(qū);軟威脅則是指與防空武器相關的安全威脅,例如地空導彈、防空火炮等。

(1) 硬威脅模型

以圓柱體作為硬威脅基本形狀,設共有M1個互不聯(lián)通的硬威脅Hm=〈Am,Pm〉,m=1,…,M1,其中Am為圓柱體中心點坐標;Pm為形狀參數(shù)矩陣,特別的,Pm=diag(a2,b2,c2)時圓柱體三軸分別與x軸、y軸和z軸平行,當a=b=c=r時Pm表示半徑為r的球體,Pm中非對角線元素不為零則表示威脅體坐標軸與航跡坐標系軸之間存在非零夾角。考慮到硬威脅三維模型中Am和Pm難以確定,在UCAV定高飛行模式下,將Am和Pm簡化為二維形式更易于計算。因此在高度為h處,硬威脅Hm可由二維中心點坐標Am(h)和形狀參數(shù)矩陣Pm(h)共同確定。

綜上UCAV硬威脅度函數(shù)可定義為

Fm(p(h))=

(13)

式中,p(h)=(x,y)表示在飛行高度為h時UCAV在2D平面內位置坐標。當Fm(p(h))<0時,UCAV可成功躲避硬威脅Hm。

(2) 軟威脅模型

與硬威脅不同,UCAV與軟威脅之間不存在碰撞問題,無人機應盡可能遠離軟威脅。設共有M2個軟威脅,飛行高度為h時,第j(j=1,…,M2)個軟威脅對UCAV的威脅度函數(shù)可表示為

Ωj(p(h))=

(14)

式中:λ(h)為與高度h有關的軟威脅強度系數(shù);Bj(h)和Qj(h)≥0分別為第j個軟威脅位置和威脅區(qū)域半徑。當UCAV以恒定高度飛行或飛行高度變化不大時,λ(h)可設為1。

軟威脅度函數(shù)Ωj(p(h))表征了UCAV位于(x,y,h)時被第j個軟威脅擊中或摧毀的概率。通過將所有軟威脅的威脅度疊加,可獲得整體軟威脅度,即

(15)

Ω(p(h))數(shù)值越小,表明UCAV受到的軟威脅程度越低。

1.4 UCAV航跡規(guī)劃目標函數(shù)

UCAV投放航跡規(guī)劃目標主要可分為3個方面:①盡可能接近機載武器投放區(qū)中心點;②避免與硬威脅發(fā)生碰撞;③盡可能遠離軟威脅。據(jù)此UCAV最優(yōu)路徑轉化為以下最優(yōu)控制問題

(16)

由于戰(zhàn)場環(huán)境具有動態(tài)多變、復雜不確定的特點,UCAV對戰(zhàn)場態(tài)勢信息很難具備準確的先驗知識,一般只能依靠其傳感器來對局部環(huán)境信息進行探測。因此,引入了模型預測控制(model predictive control,MPC)中的滾動規(guī)劃策略將航跡規(guī)劃控制在一個移動區(qū)域中滾動進行,根據(jù)其時空約束條件控制每次滾動的優(yōu)化范圍,保證無人機航跡規(guī)劃的實時性。

因此,上述航跡規(guī)劃最優(yōu)控制問題模型可進一步轉化為

(17)

式中:δ為時域長度;Δt為單位時間步長。為保證求解精度,δ和Δt取值不宜過大,但二者數(shù)值較小將導致計算負擔增大。本文中設δ=1。

2 基于威脅建模的UCAV在線航跡規(guī)劃算法

2.1 在線航跡規(guī)劃關鍵要素

設UAVi當前狀態(tài)量SUAVi(k)由二元組〈pUAVi(k),VUAVi(k)〉表示,其中pUAVi(k)=(xUAVi(k),yUAVi(k),hUAVi(k))T為無人機位置坐標,VUAVi(k)為無人機速度。為便于分析,僅考慮UCAV以定高模式飛行,即hUAVi(k)≡hUAVi。由UCAV質點運動學方程可知,單位時間步長后UCAV速度和航向角變化范圍為

(18)

[max{VUAVi+amin·Δt,Vmin},

min{VUAVi+amax·Δt,Vmax}]

(19)

UAVi與投放區(qū)中心qTi之間的視線角為

(20)

此時UAVi以最大和最小轉彎率能到的極限距離分別為

2.2 威脅規(guī)避策略

下面分別計算UCAV飛行過程中遭遇硬威脅和軟威脅時航向角的最優(yōu)變化范圍。

1) 硬威脅避碰策略

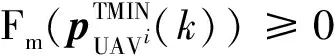
為了保證UCAV飛行安全,其航向角變化范圍為

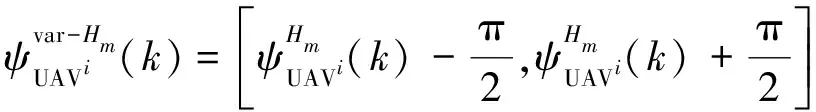
(23)

圖2 UCAV躲避硬威脅航向角變化

由圖2可得,與Pin處切線垂直的2個方向為

(24)

式中

(1) 當yUAVi(k)=ay時,有

yin=ay

(2) 當yUAVi(k)≠ay時,有

式中

2) 軟威脅躲避策略

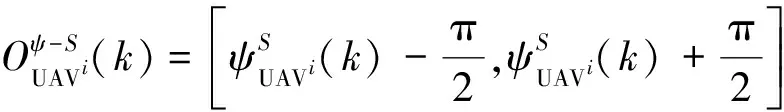
(25)

式中

2.3 基于威脅建模的在線航跡規(guī)劃流程

依據(jù)建立的硬、軟威脅模型,UCAV飛行態(tài)勢可分為以下4種情況:

Case 1 若UCAV保持當前速度飛行,大概率會與硬威脅Hm發(fā)生碰撞,UAVi需最大程度降低速度,以盡快轉彎實現(xiàn)避障;

Case 2 若UCAV繼續(xù)保持當前速度飛行,飛行器很可能進入高危區(qū)域,此時UAVi同樣需盡快降低速度,遠離高危區(qū)域;

Case 3 UCAV可安全飛行但距離投放區(qū)較遠,此時UAVi應保持當前航向,盡快飛往可投放區(qū)。

Case 4 UCAV距離投放區(qū)中心的距離已經滿足任務要求,此時UAVi應調整姿態(tài),準備完成機載武器投放。

根據(jù)上述UCAV飛行態(tài)勢分析,在線航跡規(guī)劃過程中,定義如下2個態(tài)勢判別變量

(26)

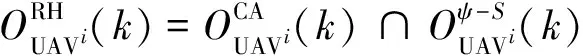
(27)

表1態(tài)勢狀態(tài)變量與UCAV飛行態(tài)勢對應關系

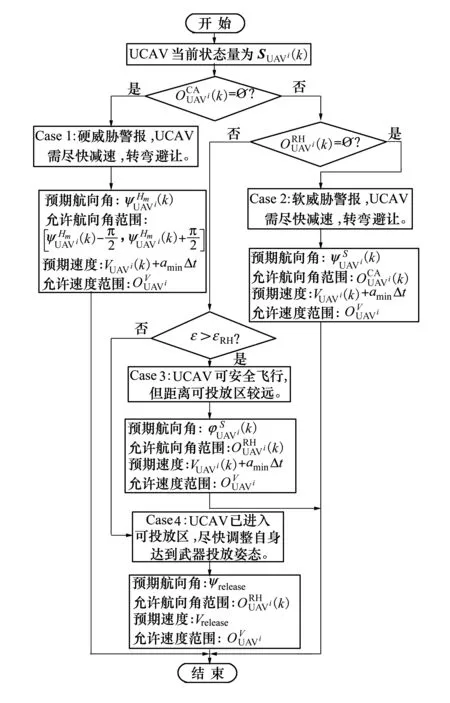
圖3 基于威脅建模的武器投放在線航跡規(guī)劃流程

3 仿真結果及分析

以攻擊型無人機執(zhí)行對地攻擊任務為例,對文中提出的武器投放航跡在線規(guī)劃算法進行仿真驗證。

設定多無人機之間為全連通通信網絡。仿真實驗環(huán)境硬件為Intel(R)Core(TM)i7-2630QM CPU 2.00 GHz,Win 7操作系統(tǒng),應用基于MATLAB R2019a的GPOPS工具包獲得控制參數(shù)。

3.1 任務環(huán)境想定

UCAV性能參數(shù)如表2所示。任務仿真想定如下:UCAV初始位置為(2,3,1.5)km,地面靜態(tài)目標位置為(14,14,0)km,初始速度為V0=200 m/s,初始航向角ψ0=135°,γ0=0,初始載油量為mfull=3 000 kg。

硬威脅為建筑物,軟威脅分別是雷達和防空導彈陣地。機載制導武器投放速度Vrelease=250 m/s,γrelease=0°,ψrelease∈[-10°,10°],αrelease=0°。C1=C2=0.5,軟威脅度閾值ξ=0.6,εRH=1 km。起始時刻為t0=0,Δt=1 s。

表2 UCAV性能參數(shù)

3.2 場景1:靜態(tài)場景航跡規(guī)劃仿真分析

場景1中UCAV起始位置為(2, 3,1.5)km,地面固定目標位于(14,14,0)km處。戰(zhàn)場環(huán)境如3.1節(jié)所示。規(guī)劃航跡結果如圖4所示(圖中紅色線條代表UCAV飛行航跡,藍色線條表示制導炸彈彈道)。算法運行時間為8.42 s,總飛行時長為90 s。

圖4 UCAV武器投放航跡

由圖4可以看出,本文所提出的在線規(guī)劃策略生成航跡較為光滑,UCAV能夠靈活避開軟、硬威脅,成功達到可投放區(qū)中心點附近。武器投放點距離可投放區(qū)中心點0.258 0 km。

3.3 場景2:動態(tài)場景航跡規(guī)劃仿真分析

為了驗證UCAV武器投放在線航跡規(guī)劃方法的可行性與有效性,場景2中對突發(fā)機動威脅和機動目標的情況進行仿真實驗。機動威脅為敵方UCAV,威脅半徑為0.5 km,其預測速度為200 m/s,預測航向角為135°。地面機動目標以30 m/s的速度朝西北方向移動。

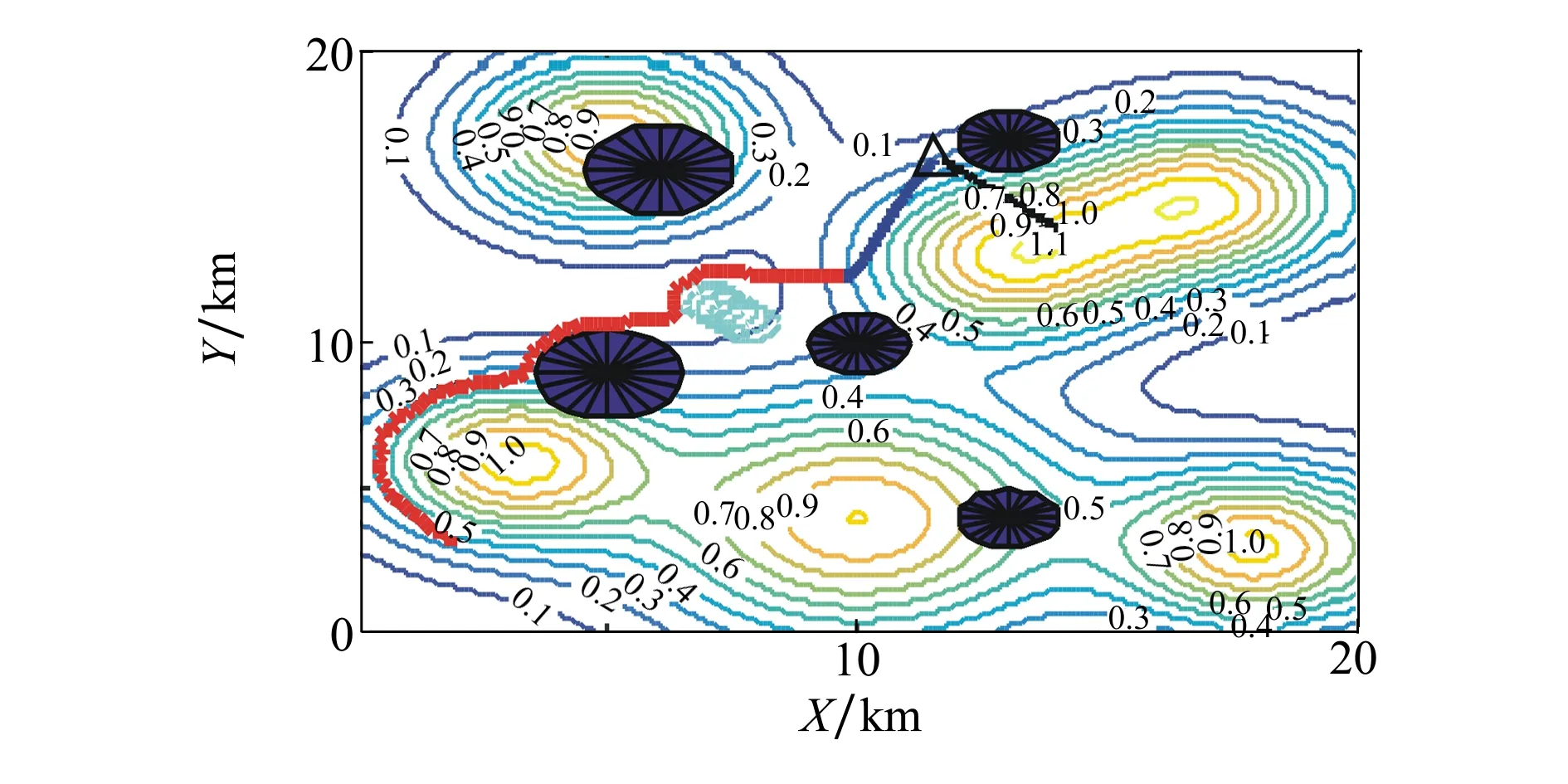
圖5 突發(fā)機動威脅和機動目標下UCAV航跡

為了直觀展示動態(tài)場景下UCAV在線規(guī)劃航跡,圖5給出了UCAV航跡的三維投影圖。圖中紅色線條代表UCAV航跡,淺藍色圓形代表突發(fā)機動威脅,深藍色線段為制導炸彈航跡,黑色線段為機動目標軌跡。算法運行時間為9.35 s,總飛行時長為94 s。武器投放點距離可投放區(qū)中心點0.032 7 km。

由圖5可知,本文所提算法可實現(xiàn)動態(tài)威脅場景下UCAV在線航跡規(guī)劃。當飛行時間為71 s時,UCAV探測到突發(fā)機動威脅,通過改變控制參量實現(xiàn)降速并調整航向,成功避開突發(fā)威脅,并最終飛抵可投放區(qū)中心附近。當t=71 s時,UCAV偵察到突發(fā)機動威脅,依據(jù)威脅規(guī)避策略UCAV。本節(jié)仿真結果展示了本文所提在線軌跡規(guī)劃算法對存在突發(fā)機動威脅和機動目標的動態(tài)場景的適用性。

3.4 算法性能比較

為進一步驗證算法性能,將本文所提航跡規(guī)劃算法與稀疏A*算法進行對比,2種算法靜態(tài)航跡對比如圖6所示,仿真參數(shù)設定同場景1。

圖6 算法靜態(tài)場景航跡對比圖

表3給出了2種算法在靜態(tài)場景下的平均威脅代價(所有航跡點威脅代價的平均值)和航跡長度。

表3 算法靜態(tài)場景性能比較

表4中,算法1為本文所提在線航跡規(guī)劃算法,算法2為稀疏A*搜索算法。

由表4可以看出,基于本文所提算法在靜態(tài)場景下規(guī)劃的航跡長度最短且總威脅代價最小。

在實現(xiàn)靜態(tài)航跡規(guī)劃基礎上隨機產生動態(tài)威脅,移動威脅參數(shù)設定同場景2,動態(tài)場景下航跡規(guī)劃仿真結果如圖7所示。

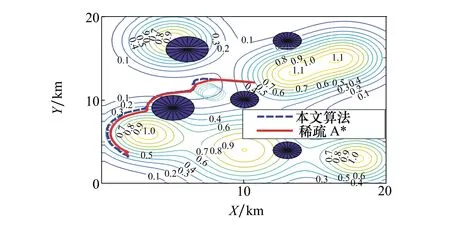
圖7 算法動態(tài)場景航跡對比圖

表4給出了2種算法在動態(tài)場景下的平均威脅代價和航跡長度。

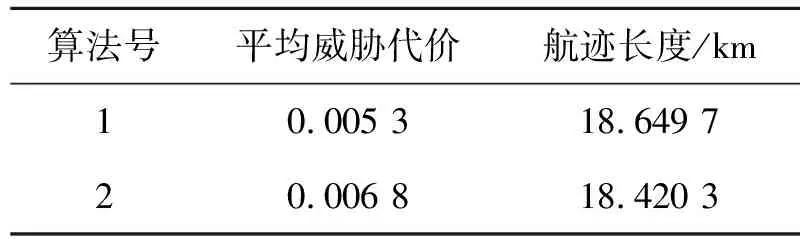
表4 算法動態(tài)場景性能比較

由表5可以看出,2種算法規(guī)劃的航跡都較好躲避了突發(fā)動態(tài)威脅,基于本文所提算法在動態(tài)場景下規(guī)劃的航跡平均威脅代價最小但飛行航跡長度稍長于SAS算法。

4 結 論

基于戰(zhàn)場環(huán)境威脅建模,本文提出了一種考慮機載武器投放約束的固定翼UCAV確定性在線軌跡規(guī)劃方法。仿真結果表明,本文設計的在線航跡規(guī)劃策略可使得UCAV在成功進入制導炸彈可投放區(qū)的同時有效避開戰(zhàn)場威脅。基于本文算法所得飛行軌跡質量隨著時間步長取值縮小而增加,但與此同時算法計算量急劇增大。因此,如何將在線軌跡規(guī)劃與基于智能優(yōu)化算法的預先航路規(guī)劃進行有效結合,并依據(jù)戰(zhàn)場環(huán)境特性實現(xiàn)在線規(guī)劃步長的自適應調整是后續(xù)研究的重點。