基于性能指標融合的隨機退化系統競爭失效分析

董慶來, 王偉偉, 司書賓

(1.延安大學 數學與計算機科學學院, 陜西 延安 716000; 2.西北工業大學 機電學院, 陜西 西安 710072)

關于隨機退化系統的研究可以追溯到20世紀60年代，但是直到20世紀90年代才引起國內外學者的重視，近年來隨著傳感器技術和計算技術的發展，隨機退化系統的可靠性建模與分析已經發展為可靠性理論與工程領域研究的熱點之一[1-4]。目前，在多元隨機退化系統的研究中，通常假設系統的退化程度由每個性能指標的退化量直接進行描述[5];除此之外，在實踐中，還經常將性能指標融合成一個變量間接地描述系統的健康狀態[6]。例如，船舶艉軸承是船舶動力裝置的主要組成部分，艉軸承間隙是描述船舶艉軸承健康狀態的重要指標，而艉軸承間隙可通過艉軸直徑磨損量和艉軸承襯磨損量來確定，當艉軸直徑磨損量和艉軸承襯磨損量之和(即將二者融合為一個新的變量)達到失效閾值(即允許的間隙最大值)時，船舶艉軸承失效[7]。楊圓鑒[7]采用Wiener過程描述艉軸直徑磨損量和艉軸承襯磨損量的退化過程，對船舶艉軸承的可靠性進行了評估，但是為了計算方便，假設二者是相互獨立的。實際上，由于受共同的工作環境及應力影響，艉軸直徑磨損量和艉軸承襯磨損量的退化過程是相關的，并且系統性能指標退化過程的相關性在許多系統中廣泛存在，因此在多元隨機退化系統的可靠性建模與分析中考慮性能指標的相關性更加符合實際，但是多元性能指標之間的相關性卻給退化建模帶來了巨大的挑戰[4,8]，其主要原因在于多元隨機過程(例如多元Wiener過程)的首達時分布是目前學術界無法解決的難題[9]。作為多元隨機退化系統的特殊情形，二元隨機退化系統是最基本、最重要的情形，是研究多元隨機退化系統的基礎，不僅能夠反映多元情形下的許多本質問題，而且相比多元情形在數學上更易于處理[10]，因此本文以二元隨機退化系統為主要研究對象。

在隨機退化系統的可靠性建模中，除了建立描述系統退化過程的退化模型，還要確定系統失效的準則，兩者缺一不可。學者們通常將系統的壽命定義為退化過程關于失效閾值的首達時間，一般稱這種失效為退化失效[11-13]。事實上，許多系統的退化過程存在警戒閾值[14]，在退化量達到警戒閾值前，系統處于正常狀態，但是超過警戒閾值后，系統將處于缺陷狀態，例如警戒水位、腐蝕裕量等[15-16]，系統在2種狀態下的退化速率通常是不同的。此時，如果采用相同參數的隨機過程對系統兩階段退化過程進行描述，可能會導致可靠性指標計算的誤差[17]。此外，上述系統除了發生因退化導致的退化失效外，系統還會發生突發失效[18-19]，例如系統在缺陷狀態的持續時間過長，系統也會失效。Dong和Cui[20]考慮退化失效和持續時間失效，構建了基于非平穩隨機過程的兩階段退化模型，給出了系統可靠度等可靠性指標。Qiu和Cui[21]考慮不同失效準則，給出了最優維修策略。上述文獻均以一元隨機退化系統為研究對象，而在二元或多元隨機退化系統的可靠性建模與分析中均只考慮退化失效[22-26]，因此探討二元或多元隨機退化系統的競爭失效分析問題具有重要的現實意義。

基于上述分析，本文的主要研究內容包括：①針對二元隨機退化系統，考慮性能指標的相關性、性能指標融合以及退化失效和持續時間失效2類競爭失效形式，構建基于二元Wiener過程的可靠性模型。②在性能指標不進行融合以及性能指標按照退化量的線性組合進行融合情形下，推導持續時間失效閾值為常數和隨機變量時的系統可靠度解析表達式。③提出基于蒙特卡洛模擬的數值模擬算法,模擬性能指標按照任意形式進行融合情形下二元以及多元隨機退化系統的可靠度，并用于驗證解析結果的正確性。

1 問題描述與可靠性建模

考慮二元隨機退化系統，根據性能指標是否進行融合，構建2個可靠性模型。性能指標融合是指利用新變量描述性能指標之間的關系，即系統的退化程度由性能指標退化量的函數進行描述。假設X(t)=(X1(t),X2(t))′,Xi(t)為系統的第i個性能指標在時刻t的退化量(i=1,2),則在性能指標融合情形下,系統在時刻t的退化程度由X(t)的函數H(x1,x2)進行描述,其中x1和x2為X1(t)和X2(t)的樣本實現值。

模型1性能指標不進行融合情形下的可靠性模型。

1) 兩階段退化過程

假設系統的退化過程包括正常階段(或第一階段,即從新系統投入運行到缺陷發生時刻)和缺陷階段(或第二階段,即從缺陷發生時刻到失效發生時刻),從而系統的狀態包括正常、缺陷和失效。令

(1)

式中:Xik(t)是系統的第i個性能指標在第k個階段時刻t的退化量,i=1,2,k=1,2;Γ1是變點,定義為2個性能指標首達警戒閾值的時刻,若定義隨機變量γi=inf{t>0:Xi1(t)≥Di1},i=1,2,則Γ1=min{γ1,γ2}。

2) 二元Wiener過程退化模型

由于受共同的環境應力,2個性能指標的退化過程是相關的,在每個階段采用二元相關Wiener過程描述系統的退化程度,即

X(t)=

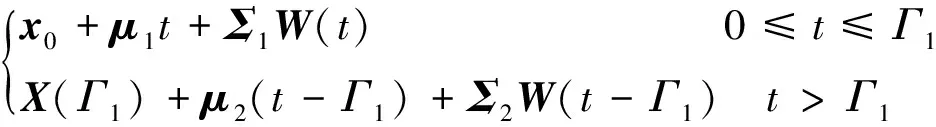
(2)

式中:x0=(x110,x210)′是系統的初始退化量,并假設x0=(0,0)′,即系統在時刻t=0是全新的;X(Γ1)=(X11(Γ1),X21(Γ1))′為系統在變點處的退化量向量。對于i=1,2,k=1,2,μk=(μ1k,μ2k)′為漂移系數向量;μik為系統第i個性能指標在第k個階段的漂移系數;Σk是第k個階段的擴散矩陣,使得

為協方差矩陣,ρk是相關系數,描述2個性能指標在第k個階段的相關性,σ1k和σ2k為標準差;W(t)=(W1(t),W2(t))′,{W1(t),t≥0}和{W2(t),t≥0}是相互獨立的標準Wiener過程。具體的,如果記

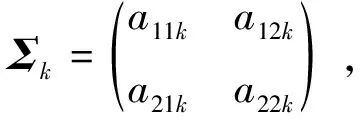
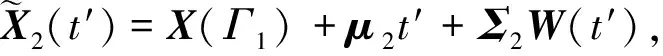
3) 競爭失效

當一個性能指標的退化量超過其退化失效閾值時,或系統在缺陷階段的持續時間超過持續時間失效閾值τ時,系統失效。系統的退化路徑如圖1所示,其中γ和y分別為Γ1和Y的實現值。

圖1 模型1下系統的退化路徑

因此,模型1下系統的壽命為

Y1=min{Λ1,τ}+Γ1

(3)

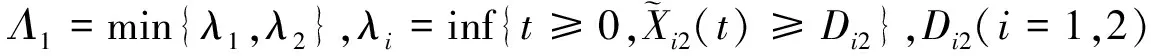
模型2性能指標融合情形下的可靠性模型。

本文考慮H(x1,x2)的3種表達形式:

①H(x1,x2)=k1x1(t)+k2x2(t),k1,k2∈R;②H(x1,x2)=|x1(t)-x2(t)|;③一般形式。

與模型1的不同之處在于變點以及系統壽命的表達形式。在模型2下,變點定義為2個性能指標退化量的函數關于警戒閾值L1的首達時刻,即

Γ2=inf{t≥0:H(X11(t),X21(t))≥L1}

(4)

則系統的壽命為

Y2=min{Λ2,τ}+Γ2,

(5)

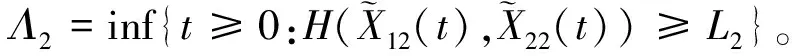
2 系統可靠度

本節將給出系統可靠度的解析表達式,包括模型1和模型2下H(x1,x2)=k時2種情形,以及模型2下H(x1,x2)為一般函數時可靠度的模擬算法。

1) 模型1下系統可靠度

根據失效準則,系統的可靠度為

R(t)=P{Y1>t}=P{min{Λ1,τ}+Γ1>t}

(6)

首先,假設持續時間失效閾值為常數。

注意到Γ1=min{γ1,γ2}以及γi=inf{t≥0:Xi(t)≥Di1},i=1,2,通過對一個性能指標達到失效閾值的時刻及另一個未達到失效閾值的性能指標在該時刻的數值取條件,得到

(7)

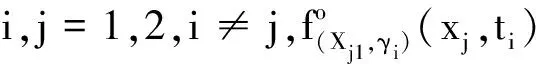
當其中的一個性能指標達到失效閾值時,系統將進入缺陷階段。根據Xi2(t)(i=1,2)的定義,當

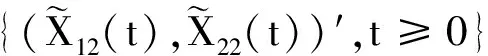
(8)

式中,f(λ1,λ2)(u1,u2|x0i)的表達式由文獻[27]的公式(2)給出。將(8)式代入(7)式,得到

(9)

在工程實踐中,持續時間失效閾值通常是隨機變量。下面假設持續時間失效閾值是具有概率密度函數fτ(t)和分布函數Fτ(t)的隨機變量,并考慮以下2種情形：一種情形是分布在[0,+∞)上的隨機變量;一種情形是分布在[τ1,τ2]上的隨機變量,其中τ1和τ2是正常數。

如果持續時間失效閾值τ是分布在[0,+∞)上的隨機變量,例如τ是服從指數分布或韋布爾分布的隨機變量,則(9)式變為

類似的,可以得到持續時間失效閾值τ是分布在[τ1,τ2]上的隨機變量時的可靠度。

2) 模型2下H(x1,x2)=k時系統可靠度

根據Γ2的定義,如果τ是常數,系統可靠度為

(10)

式中:f(X1,Γ2)(x1,u)是X1(Γ2)和Γ2的聯合概率密度函數,滿足

f(X1,Γ2)(x1,u)=fX11(u)(x1)fΓ2(u)

(11)

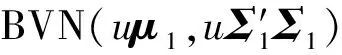
(12)

從而,要得到(11)式的解析表達式,只需得到變點Γ2的概率密度函數fΓ2(u)即可。然而,除了H(x1,x2)的一些特殊形式外,fΓ2(u)的解析表達式是很難獲得的。

下面,給出H(x1,x2)=k1x1+k2x2情形下的系統可靠度。由(2)式知

H(X11(t),X21(t))=(k1μ11+k2μ21)t+δ1B1(t)

(13)

式中，{B1(t)=[(k1a111+k2a211)W1(t)+(k1a121+k2a221)W2(t)]/δ1,t≥0}是標準Wiener過程，

由Γ2的定義,即Γ2=inf{t>0:H(X11(t),X21(t))≥L1},fΓ2(u)為{Z1(t),t≥0}關于L1的首達時的概率密度函數,其中Z1(t)(k1μ11+k2μ21)t+δ1B1(t)。因此,由(13)式可以得到

(14)

將(12)式和(14)式代入(11)式,得到

(15)

接下來,給出FΛ2(t-u|x1,x2)的解析表達式。注意到k1x1+k2x2=L1,與(13)式類似

L1+(k1μ12+k2μ22)t+δ2B2(t),t≥0

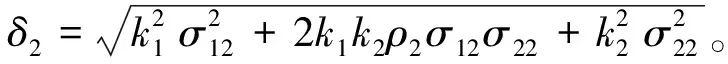
(16)

將(15)式和(16)式代入(10)式,得到H(x1,x2)=k1x1+k2x2情形下的系統可靠度

(17)

注：①如果令τ=0,(17)式將變為單階段一元隨機退化系統的可靠度[11];②如果令τ→+∞,(17)式將變為兩階段一元隨機退化系統的可靠度[11];③如果τ是隨機變量,通過積分可以得到相應的系統可靠度的解析表達式。

3) 模型2下H(x1,x2)為一般函數時系統可靠度的數值模擬

由(11)式可以發現,性能指標按照任意形式進行融合情形下的系統可靠度表達式在形式上是簡單的,但是對一般H(x1,x2)而言,Λ2和Γ2的分布函數的表達式并不容易求解。基于蒙特卡洛模擬的算法來模擬系統可靠度,具體的模擬算法流程如算法1所示。

算法1模型2下H(x1,x2)為一般函數時系統可靠度的模擬算法

步驟1設定參數值,包括初始時刻t=0,初始退化量x0,漂移參數向量μ1和μ2,擴散矩陣Σ1和Σ2,警戒閾值L1,退化失效閾值L2,持續時間失效閾值τ和其他相關參數。令模擬次數和步長分別為N和Δt。

步驟2對于i=1,2,…,N,執行步驟3至4。

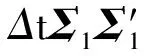
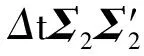
步驟5完成模擬,根據失效數據集A計算系統可靠度。

注：1) 如果持續時間失效閾值是隨機變量,只需在步驟4中增加在指定的分布中生成獨立同分布的隨機數即可。

2) 算法1還適用于基于性能指標融合的多元隨機退化系統的可靠度計算,即隨機退化系統具有多個性能指標(例如n個性能指標)時,只需做如下修改:①在步驟3和步驟4中生成多元正態分布隨機數,即擴散矩陣Σ1和Σ2分別為n×n階矩陣;②采用H(x1,x2,…,xn)描述性能指標融合,即將各性能指標退化量的數值代入H(x1,x2,…,xn)描述系統的退化程度。

3 數值算例

本節給出一些數值算例來驗證所構建模型的有效性,并對模型中的參數進行靈敏度分析,探討模型參數對隨機退化系統可靠性指標的影響。

假設2個性能指標退化量的警戒閾值和退化失效閾值分別為0.2和0.4,持續時間失效閾值τ=4。在第一階段,μ11=μ21=0.016 7,σ11=σ21=0.045 0,ρ1=-0.786 2;在第二階段,μ12=μ22=0.024 0,σ12=σ22=0.060 4,ρ2=-0.694 3,從而兩階段的協方差矩陣分別為

1) 模型1下系統可靠度

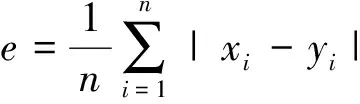
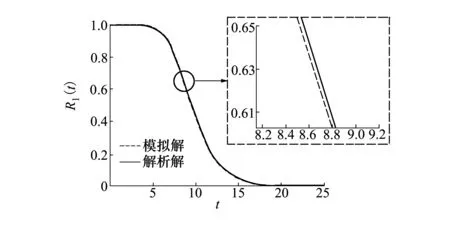
圖2 模型1下基于模擬解和解析解的系統度曲線

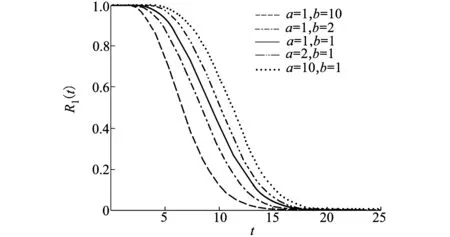
圖3 持續時間失效閾值服從β分布情形下系統可靠度曲線

2) 模型2下H(x1,x2)=k1x1+k2x2時系統可靠度

假設系統的警戒閾值、退化失效閾值和持續時間失效閾值分別為0.3，0.5和4.0,其余參數取值與圖3相同。為了描述2個性能指標退化量的線性組合對系統可靠度的影響,考慮k1和k2取不同參數值情形下的系統可靠度,即:k1=1.5且k2=1.2、k1=1且k2=1、k1=0.5且k2=0.5、k1=0.4且k2=0.3、k1=1且k2=0。將可靠度曲線畫在同一個圖中,如圖4所示,其中k1=1且k2=0時的系統可靠度曲線可以看作一元隨機退化系統的可靠度曲線。

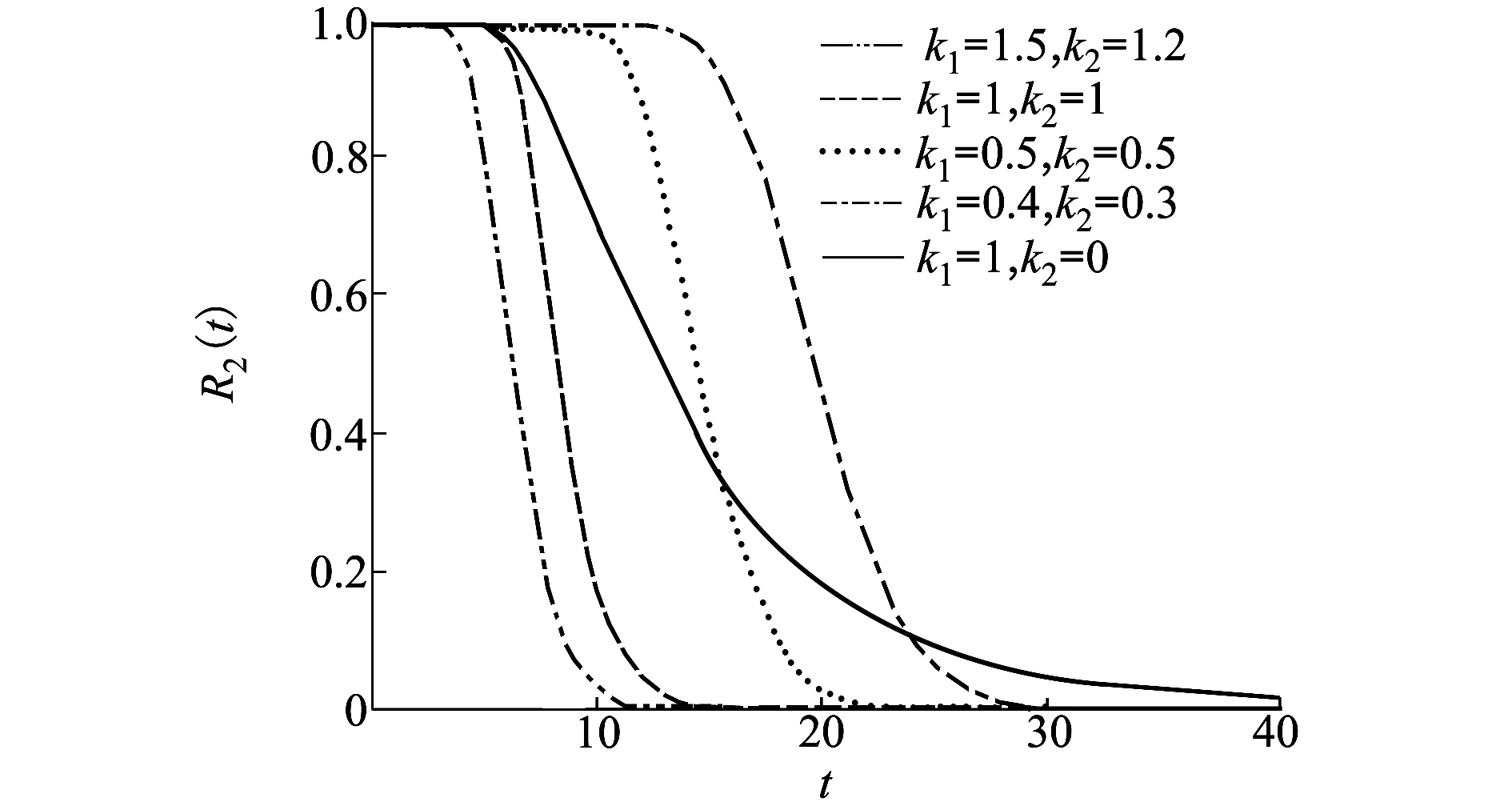
圖4 H(x1,x2)=k1x1+k2x2情形下系統可靠度曲線

從圖4可以發現,k1和k2的值越大,系統的可靠度越低。這是因為k1和k2反映了2個性能指標退化量對系統整體退化量的貢獻,它們的值越大,說明系統的退化速度越快,從而系統的可靠度越低,這與我們的直覺是一致的。另一個現象是,當k1和k2的取值較小時,其可靠度在退化過程的早期階段高于單變量Wiener過程退化模型的結果,而在退化過程的后期結果卻相反,這可以用2個性能指標的相關性(2個性能指標是負相關的)來解釋。

3) 模型2下H(x1,x2)=|x1-x2|時系統可靠度分析

不等式|x1-x2|>L1曾被Cui等[8]用作平衡系統的失效準則,即當2個性能指標退化量的距離大于失效閾值L1時,系統失效;采用Markov過程描述2個性能指標的退化過程,并假設它們是相互獨立的。下面,利用算法1給出2個性能指標相關時采用函數H(x1,x2)=|x1-x2|描述系統退化程度情形下的系統可靠度曲線。假設τ=0,L1=0.1,即只考慮單階段退化過程。為了得到2個性能指標之間的相關性對系統可靠度的影響,分別令ρ1=-0.8，-0.5，0，0.5和0.8,將可靠度曲線畫在同一個圖中,如圖5所示。其余參數取值與圖2相同。從圖5可以發現,在其余參數值相同的情形下,相關系數ρ1的值越大,系統的可靠度越高。因此,2個性能指標的退化過程是正相關(或負相關)時,如果假設它們彼此獨立,則會低估(或高估)系統可靠度。

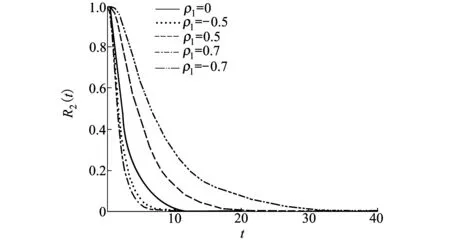
圖5 模型2下H(x1,x2)=|x1-x2|時單階段隨機退化系統可靠度曲線

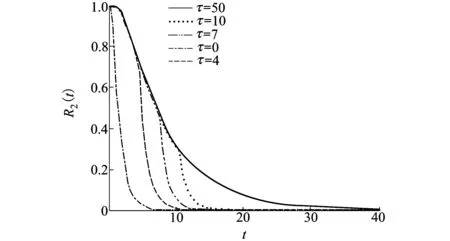
圖6 模型2下H(x1,x2)=|x1-x2|時兩階段隨機退化系統可靠度曲線

進一步,為了探究持續時間失效閾值對系統可靠度的影響,假設L1=0.1,L2=0.3,其余參數取值與圖3相同,考慮τ取不同參數值情形下的系統可靠度,包括τ=0,4,7,10和50,并將可靠度曲線畫在同一個圖中,如圖6所示。從圖6可以發現,持續時間失效閾值越小,系統的可靠度越低。這意味著系統處于缺陷階段的可承受時間越短,系統發生失效的可能性越大,這與文獻[20]的結論是一致的。

4 結 論

本文針對二元隨機退化系統，考慮性能指標融合以及競爭失效，提出了基于二元相關Wiener過程的退化模型，給出了性能指標不進行融合以及性能指標按照退化量的線性組合進行融合情形下，持續時間失效閾值為常數和隨機變量時的系統可靠度的解析表達式。當性能指標按照任意形式進行融合時，提出了一個算法程序來模擬系統的可靠度。研究結果表明持續時間失效閾值越大，系統的可靠性越高。此外，當性能指標按照2個性能指標退化量的距離進行融合時，若2個性能指標正相關(或負相關)而假設它們彼此獨立，則會低估(或高估)系統可靠度。因此，在工程實踐中，如果存在2個(或多個)性能指標，應充分考慮它們的相關性，從而提高可靠性指標計算的精度。此外，本文給出的算法盡管能夠用于性能指標按照任意形式進行融合情形下二元以及多元隨機退化系統可靠度的模擬，但是由于該算法是基于蒙特卡洛模擬的，因此算法的精度強烈依賴于模擬次數，因此在今后研究中尋求系統可靠度的解析表達式以及其他算法將更加有意義。