基于貝葉斯網絡的渦軸航空發動機性能優化策略

王寧, 王宇航, 蔡志強, 張帥

(1.長安大學 運輸工程學院, 陜西 西安 710064; 2.西北工業大學 機電學院, 陜西 西安 710072)

渦軸航空發動機一般應用在直升機上，通過與旋翼配合構成動力裝置，相比于此前的活塞式發動機，有著體積小、重量輕、功率大等多種優勢，近年來得到了快速發展與廣泛關注[1]。渦軸發動機的生產過程復雜，需要遵循非常細致的制造手冊，同時，在出廠檢測中對其各項性能指標都設定了嚴格的要求。關鍵截面溫度是渦軸發動機的一個常見性能指標。當關鍵截面溫度過高時有可能會對發動機中的關鍵部件造成損壞，從而引發重大安全事故，因此為了確保發動機的工作壽命以及飛機的安全性，關鍵截面溫度這一指標有最高溫度限制。然而，在當前的技術條件下，制造出來的發動機很難做到一次試車即能滿足該指標的出廠合格要求，通常需要重新裝配之后嘗試2次乃至3次試車，這大大增加了渦軸發動機的制造成本。

近年來，隨著人工智能技術的發展，許多研究人員將人工智能算法引入到了航空發動機的優化設計中。孫浩等[2]基于人工神經網絡和GMM聚類建立了航空發動機的經驗模型，為發動機的健康參數監測做出了貢獻。李樂等[3]采用數據后處理修正的方法，對航空發動機現有的燃氣取樣及分析系統進行了優化設計，有效提高了分析精度與穩定性。Ahmadian等[4]研究了噴氣發動機的多模型自適應控制方法，在Jet Cat SPT5型渦軸發動機上的仿真結果證明了該方法的有效性。從趨勢分析的角度，John等[5]提出了一種用于渦軸發動機試驗臺標定的新方法，該方法被證實可以極大節省人力和物力成本。董楨等[6]提出了一種基于粒子群優化算法的發動機部件特性自動修正及更新方法，有效提高了渦軸發動機部件級模型的精度,并直接輸出更新后的部件特性。陳必東等[7]提出一種渦軸發動機綜合系統中抗干擾控制性能的優化解決辦法。針對發動機單個部件性能對整機性能的影響權值難以定量的問題,林學森等[8]提出采用隨機賦權值的極限學習機算法診斷發動機部件性能退化。

得益于計算機技術的迅速發展，貝葉斯統計后驗分布求解的難題得到了較好的解決，再加上貝葉斯統計在經濟學、社會學和醫學等領域的成功應用，使得貝葉斯網絡的理論和應用飛速發展[9]。在故障診斷領域，也有大量的研究人員將貝葉斯網絡用在了裝備故障預測以及診斷優化上，均取得了不錯的進展。

本文將貝葉斯網絡引入渦軸發動機的性能優化中，以關鍵截面溫度為目標變量建立了渦軸發動機性能模型，通過貝葉斯網絡搜索的方式，得到了用于指導生產的推薦狀態組合表，可以有效提高發動機的出廠合格率。

1 貝葉斯網絡理論

1.1 貝葉斯網絡

貝葉斯網絡是對復雜不確定系統進行概率推理以及數據挖掘的一種可靠工具，如今已經成為機器學習領域的一個熱點研究方向[10]。貝葉斯網絡將圖論、概率論和統計學理論融合到了一個模型中，是一種高效地呈現事件之間相互關系的建模語言，他能將知識以圖形的形式直觀表示，使知識系統可視化。貝葉斯網絡是一種概率圖模型，變量間的依賴關系以一種網絡結構的形式來呈現[11-13]。他提供了一種自然地表示因果信息的方法，可以用來發現數據間的潛在關系[14]。

貝葉斯網絡的拓撲結構為有向無環圖,其中節點代表隨機變量,而有向邊則代表變量之間的相互作用關系。每個節點都有著相應的條件概率,根節點X伴隨的是其邊緣分布P(X),而非根節點X伴隨的是條件概率分布P(X|ap(X)),ap(X)表示節點X的父節點[15]。

1.2 聯合概率分解

針對一個含有n個隨機變量X1,X2,…,Xn的貝葉斯網絡,將各節點所對應的概率分布相乘即可得到這n個隨機變量的聯合概率分布

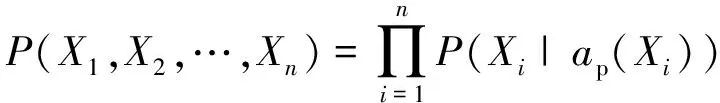
(1)

式中,ap(Xi)為節點Xi的父節點,當ap(Xi)=?時,P(Xi|ap(Xi))即為邊緣分布P(Xi)。

在圖1中給出了一個常見的貝葉斯網絡,根據(1)式可以得到一個聯合概率分布的分解

P(A,B,C,D,E)=

P(A)P(B)P(C|A,B)P(D|C)P(E|C)

(2)

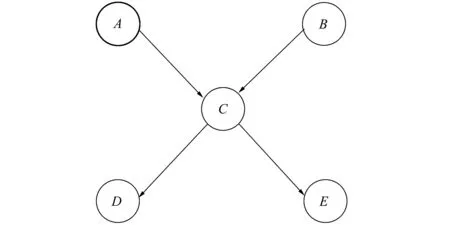
圖1 貝葉斯網絡模型

1.3 樸素貝葉斯模型

樸素貝葉斯(NB)模型[16]又被稱作樸素貝葉斯分類器,是一種含有一個目標變量和多個屬性變量的樹型貝葉斯網絡。圖2是一個樸素貝葉斯模型的示例,其中C代表目標變量,A1,A2,…,An代表屬性變量。當已知各屬性變量的取值時,通過計算后驗分布P(C|A1=a1,…,An=an)來進行分類,找出后驗概率最大的那個C值劃分為對象的預測類別。

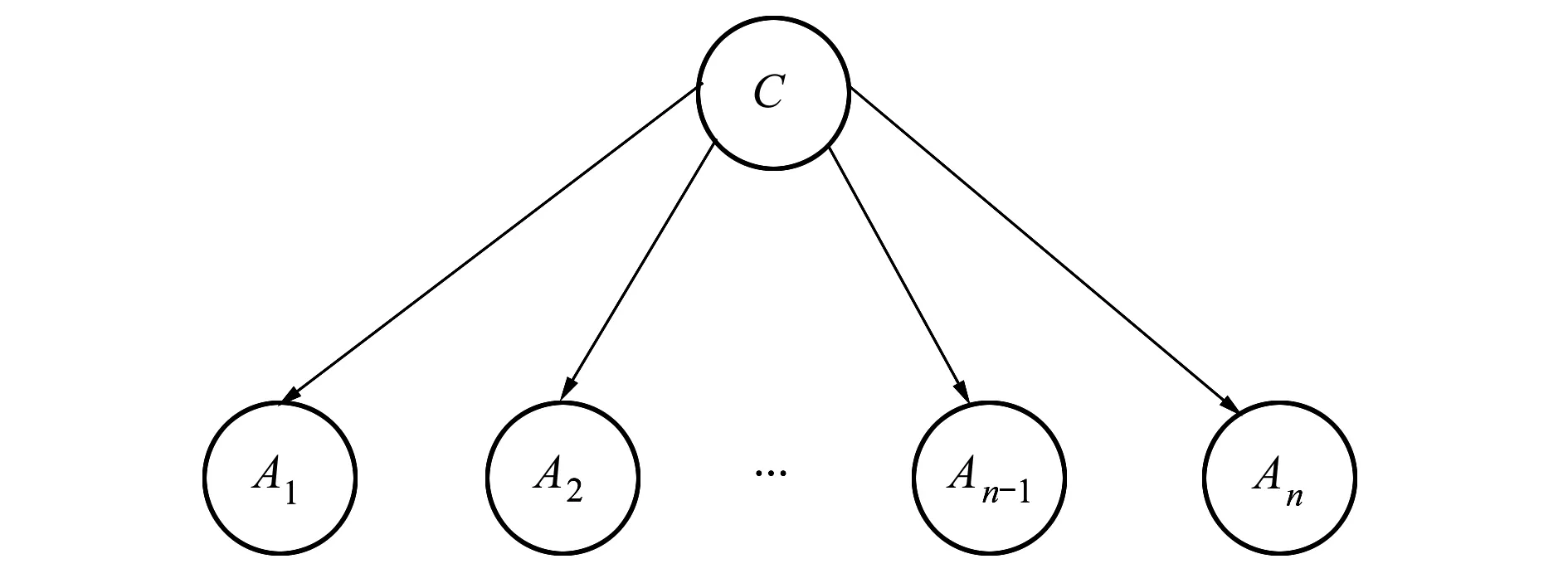
圖2 樸素貝葉斯模型

樸素貝葉斯模型存在一個局部獨立性假設,這表明在已知類別變量C時,各屬性變量Ai之間相互條件獨立,因此這個模型的聯合概率分布是

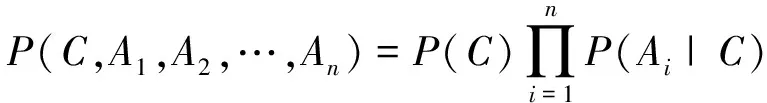
(3)

2 基于貝葉斯網絡的發動機性能模型

2.1 優化目標與數據提取

在實際生產過程中發現改變零件1、零件2以及零件3的大小(X,Y,Z)會對某型號產品的關鍵截面溫度(T)造成顯著影響。除此之外,T還受到外界氣溫(Tout)的影響。此外,在充分考慮安全性的情況下,渦軸發動機在運行時T最高不得超過895℃。因此本文的優化目標是找到一些表現良好的X-Y-Z-Tout的組合方式,從而盡可能提高渦軸發動機出廠時T符合要求的概率。

結合制造商的建議,本文提取出了含有5個變量:T,X,Y,Z和Tout的228條某型號渦軸發動機數據。其中,T是要優化的目標變量,其余的4個變量為屬性變量。渦軸發動機數據集的各變量描述及取值范圍如表1所示。

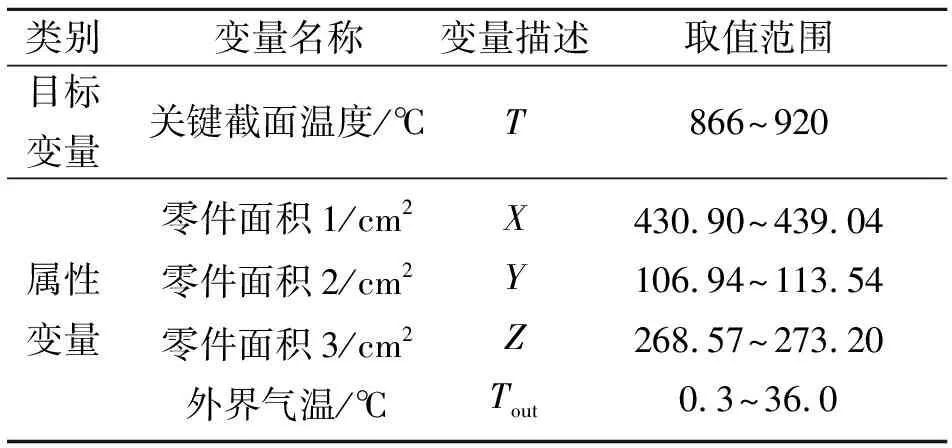
表1 渦軸發動機數據集變量情況統計

2.2 離散化處理與數據集劃分

進行貝葉斯網絡建模的關鍵步驟是變量的離散化。針對目標變量T,以最高合格值895℃為界將其分為2段。對于屬性變量Tout,以10℃和25℃為界將其分為3段。對于屬性變量X,Y,Z,考慮到生產加工的方便,采用等頻率離散法將他們各自分為3段。離散化后的數據集見表2。

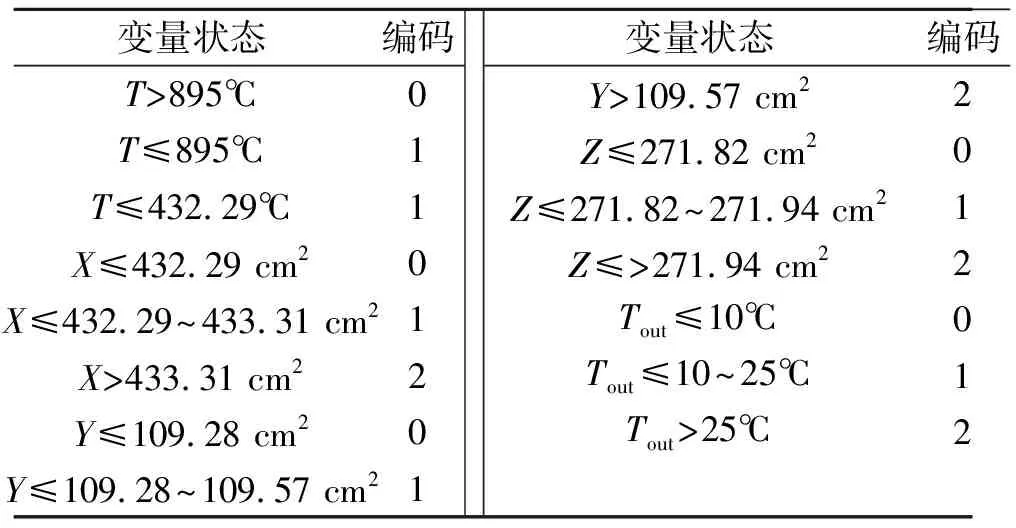
表2 數據集離散化結果

考慮到模型的有效性驗證,進一步將數據集采用分層抽樣的方法隨機分割,其中的80%作為訓練集,剩余的20%作為測試集用來檢驗模型的預測效果,訓練集和測試集中目標變量T的類別比例保持一致。渦軸發動機數據集的劃分方式如表3所示。

表3 數據集劃分結果

2.3 發動機性能模型的建立

在數據準備工作完成之后,接下來基于樸素貝葉斯模型建立以T為目標變量的渦軸發動機性能模型。

首先,基于樸素貝葉斯模型建立了渦軸發動機性能模型網絡結構,如圖3所示,這種有向無環圖是貝葉斯網絡模型的定性部分。其中,目標變量T作為父節點,其余的4個屬性變量X,Y,Z和Tout則作為子節點。

然后,需要計算目標變量的概率分布表以及各屬性變量的條件概率表。通過對訓練集中各個特定類型的樣本頻率進行統計,得到了表4至8。

表4 目標變量T的概率分布表

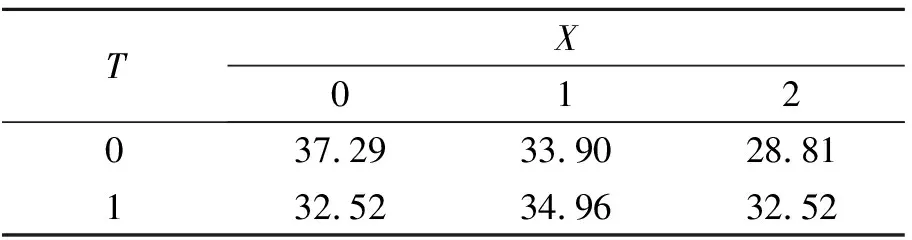
表5 屬性變量X的條件概率表 %

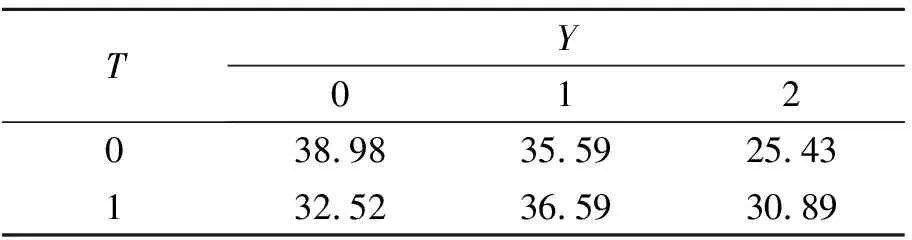
表6 屬性變量Y的條件概率表 %

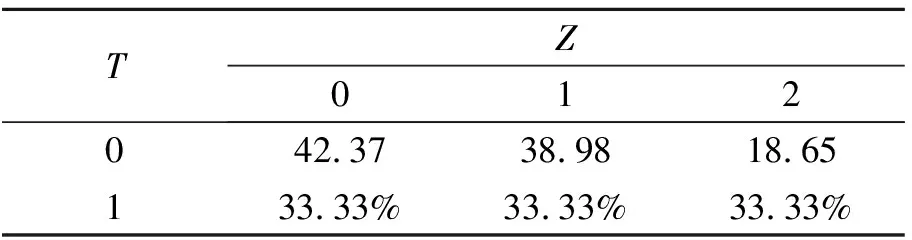
表7 屬性變量Z的條件概率表 %

表8 屬性變量Tout的條件概率表 %

表4至8中的概率關系屬于貝葉斯網絡模型的定量部分,將各個變量之間的依賴關系通過概率的形式來量化表示。

3 渦軸航空發動機性能優化策略

在完成性能模型的構建之后,下一步應該考慮的是如何基于模型來優化渦軸發動機的性能。本節將根據貝葉斯網絡的概率推理特性對性能模型進行搜索,找到一些高質量的屬性變量的狀態組合,從而提高渦軸發動機的合格率。

3.1 后驗合格概率的計算

首先,需要列出所有可能的屬性變量狀態組合。在本研究中,有4個屬性變量X,Y,Z和Tout,每個屬性變量又分為3種狀態(0,1,2),因此可能的狀態組合總共有34=81種。然后,將這些狀態組合依次輸入到性能模型中,通過概率推理進行后驗合格概率的計算。

為了對具體的計算過程進行說明,接下來以X,Y,Z和Tout的狀態組合為(0,0,0,0)時為例,計算該狀態組合下目標變量T的后驗合格(T=1)概率。計算過程如下:

首先根據貝葉斯公式,當T=1時有

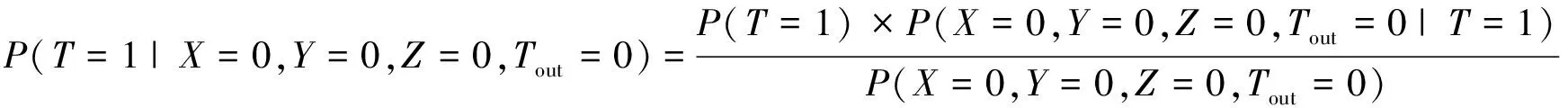
(4)

根據圖3,可對(4)式進一步化簡

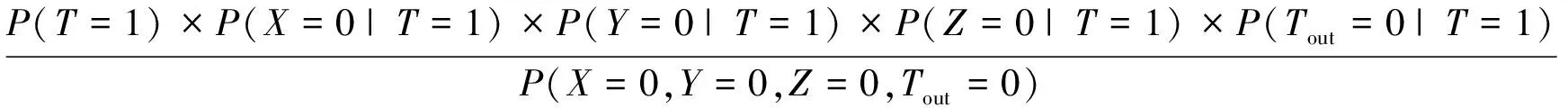
(5)

在(5)式中,分子中的P(T=1)可通過查詢表4得到,P(X=0|T=1)等4個屬性變量的條件概率值可分別通過查詢表5至8得到。將分母保持固定,令D=P(X=0,Y=0,Z=0,Tout=0)以便于描述。將查得的各個數值代入(5)式,可以得到

(6)

同理,當T=0時有

(7)

根據概率論知識,由(6)式和(7)式可得

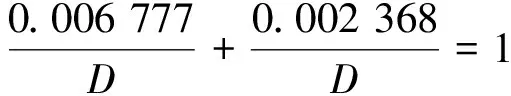
(8)

解(8)式可得D=0.009 145,代入(6)式可得

P(T=1|X=0,Y=0,Z=0,Tout=0)=

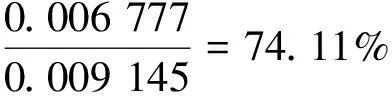
(9)

至此,便可得到:當X,Y,Z和Tout的狀態組合為(0,0,0,0)時,目標變量T的后驗合格概率為74.11%。將本研究全部81種可能的屬性變量組合輸入到性能模型中,按上述計算過程進行概率推理,就可以得到所有屬性變量狀態組合下目標變量T的后驗合格概率結果。

3.2 對比驗證

在通過概率推理完成后驗合格概率的計算之后,有必要對所建立的性能模型進行有效性驗證。將之前劃分好的測試集輸入到建立好的性能模型中,通過比較目標變量的預測值與實際值,得到了性能模型的混淆矩陣,見表9。

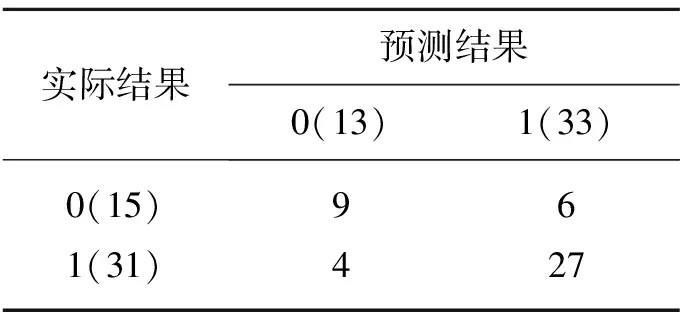
表9 混淆矩陣

通過混淆矩陣,還可進一步計算得到更多性能評價指標,如準確率、精確率、召回率(recall)和F1值等。

進一步地,為了驗證本文所建立的樸素貝葉斯性能模型(NB)的有效性,在此引入機器學習算法中常見的決策樹(DT),邏輯回歸(LR)和隨機森林(RF)進行模型的對比。各個模型在同一測試集上的性能表現如表10所示。

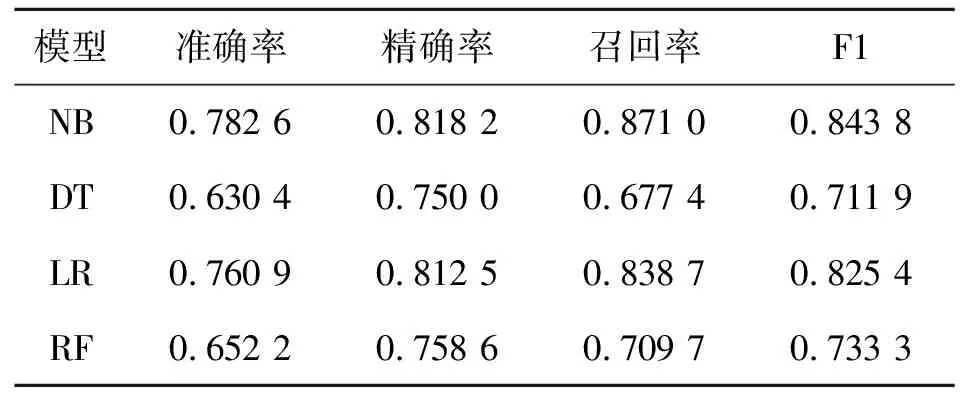
表10 模型性能計算結果

為方便比較,對表10的計算結果進行了可視化展示,如圖4所示。

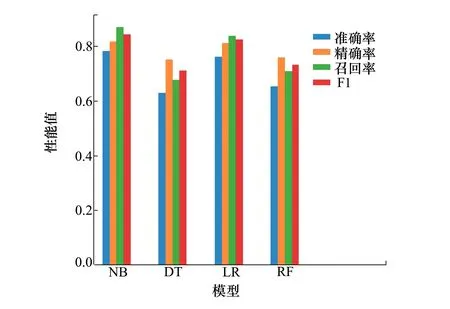
圖4 模型性能對比

從以上結果可以看出,本文基于樸素貝葉斯模型建立的渦軸航空發動機性能模型具有較高的精度,能較好地體現數據的特點。在與其他模型的對比中,綜合各個性能指標來看有比較大的優勢,基于此模型所進行的概率推理相較來說也最為可信。

3.3 推薦狀態組合表

通過排列屬性變量的狀態組合并將其依次輸入到性能模型中,得到目標變量T的后驗合格概率之后,可以按概率值大小對這些狀態組合做一個降序排列,形成一個推薦狀態組合表。在推薦狀態組合表中所處的位置越高,表示采用該狀態組合后,目標變量T滿足合格條件的概率就越大。受篇幅限制,本文只節選了推薦狀態組合表中的前20個狀態組合,如表11所示。

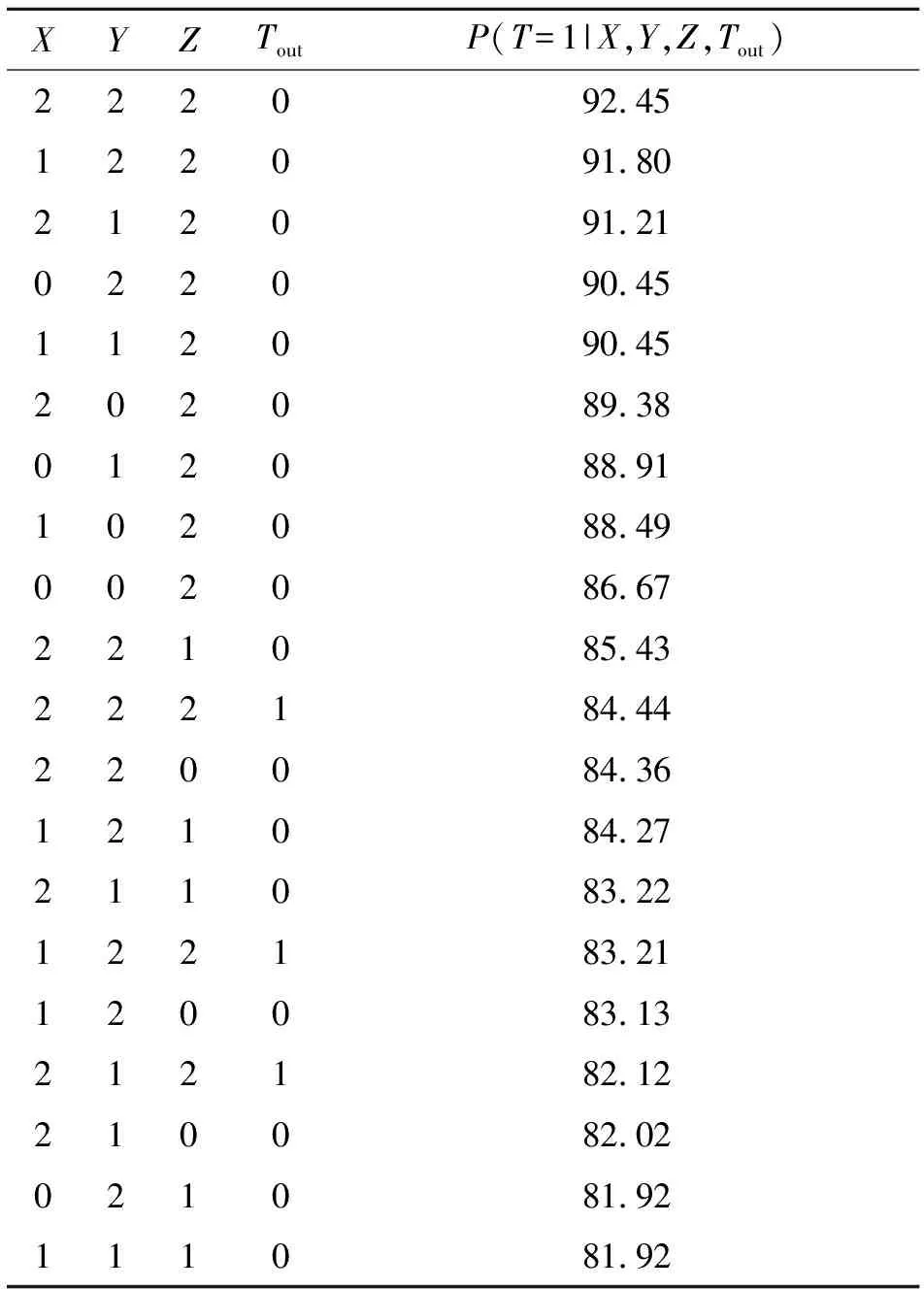
表11 推薦狀態組合表(節選)

根據表11可以發現,能使目標變量T的后驗合格概率最大的屬性變量X,Y,Z和Tout的狀態組合為(2,2,2,0),在采用了該狀態組合后,理論上目標變量T有92.45%的概率能滿足合格要求。此外,還可進一步設定搜索目標,假如需要找出全部滿足目標變量T的后驗合格概率≥85%的狀態組合,根據表11,可輕松得到:在此搜索目標下,屬性變量X,Y,Z和Tout的狀態組合解集為{(2,2,2,0),(1,2,2,0),(2,1,2,0),(0,2,2,0),(1,1,2,0),(2,0,2,0),(0,1,2,0),(1,0,2,0),(0,0,2,0),(2,2,1,0)}。

基于貝葉斯網絡的概率推理特性對性能模型進行搜索，成功建立了渦軸發動機的推薦狀態組合表。在以后的實際生產與裝配活動中，可以適當綜合考慮經濟成本和人力成本，盡可能選擇在推薦狀態組合表中排名靠前的參數狀態組合，從而可以有效提高渦軸發動機的出廠合格率。不同于常規的貝葉斯網絡應用模式，在經過模型搜索之后，成功實現了由模型出發反過來指導生產的目標。

4 結 論

本文主要研究渦軸航空發動機的性能優化問題，首先對渦軸發動機的數據進行了提取與預處理，然后，利用樸素貝葉斯模型，建立了以關鍵截面溫度為目標變量的渦軸發動機性能模型。接著，基于貝葉斯網絡的概率推理特性對性能模型進行了后驗合格概率的計算，并引入決策樹，邏輯回歸和隨機森林等主流算法進行對比分析，結果表明本文所提出模型能夠有效識別發動機的性能合格概率。最后，提出了推薦狀態組合表，對渦軸航空發動機的日常生產活動提出了切實有效的建議。