基于分數階線性系統初態學習的PDα-型迭代學習控制

劉芬, 張克軍

(1.西北工業大學 航海學院, 陜西 西安 710072; 2.延安大學 數學與計算機科學學院, 陜西 延安 716000；3.徐州工程學院 數理學院, 江蘇 徐州 221111)

迭代學習控制(ILC)[1]是一種簡單有效的學習控制策略,適用于在固定有限時間間隔內重復運行的被控系統。在足夠的學習時間,可以用較少的先驗模型知識和較少的在線計算來提高系統的跟蹤性能。基于其優勢,ILC已經成為研究熱點,廣泛應用于移動機器人、工業過程控制、交通信號控制等多個領域[2-4]。2001年,Chen等[5]首次提出了PDα-型分數階迭代學習控制算法,在頻域內討論了算法的收斂性,并將迭代學習控制的應用范圍推廣到分數階系統,即分數階迭代學習控制(FOILC)。FOILC除了具有傳統迭代學習控制的優點外,還可以提高具有分數階特性的被控系統的性能。近年來,FOILC在時域方面取得了豐碩的成果,Lazarevic等[6-7]證明了PDα-型、開閉環PDα-型分數階迭代學習算法的收斂性和穩定性。Li等[8-9]提出了幾種分數階迭代學習算法,并討論了其收斂性和穩定性。lan等[10]研究了Dα-型分數階迭代學習算法的收斂性問題。

在上述FOILC設計過程中,一般都是假定所研究被控系統在每一次的迭代過程中初態都與期望初態一致。但是在實際問題中,系統的期望初始狀態通常是未知的,不可能保證初始狀態值等于期望的初始狀態值。因此,研究具有初始狀態偏差的系統控制算法的魯棒性是非常重要的。迄今為止,關于分數階系統的初態問題的研究還很少。對于一類具有固定初始狀態誤差的分數階線性定常系統,文獻[11]首次提出了一種具有初始狀態學習的開閉環P型ILC算法,得到了算法收斂的充分條件。文獻[12]設計了具有初始狀態學習的開環和閉環P型ILC方案。文獻[13]將上述算法應用于一類分數階非線性時滯系統。文獻[14]針對一類具有初始狀態漂移的分數階線性定常系統,提出了一種新的修正PDα-型FOILC算法。

目前對分數階系統的跟蹤控制研究中,主要是利用λ-范數對跟蹤誤差進行測量。與λ-范數相比,Lebesgue-p范數更適合分析控制算法的學習行為[15-18]。

基于上述問題,本文針對一類具有任意初始狀態的分數階線性時不變系統,提出了具有初始狀態學習的開環和開閉環PDα-型FOILC算法,并在Lebesgue-p范數意義下分析了算法的收斂性。

1 預備數學知識

本節首先給出一些相關的數學知識。

定義1對于連續時變向量函數

f:[0,T]→Rn,(f(t)=[f1(t),f2(t),…,fn(t)]T)

則λ-范數和Lebesgue-p范數分別為

引理1[18]設函數g(t),h(t)(t∈[0,T])為勒貝格積分,若函數g(t)與h(t)的卷積

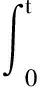
存在,則卷積積分的廣義Young不等式為

‖(g*h)(t)‖r≤‖g(t)‖q‖h(t)‖p

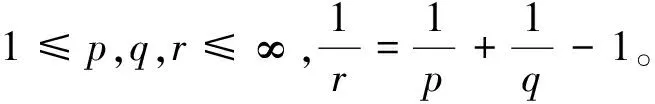
‖(g*h)(·)‖p≤‖g(t)‖1‖h(t)‖p

定義2Riemann-Liouville′s(R-L)的左側和右側分數階積分的定義為

式中,α>0,Γ(·)為Gamma函數。

Caputo左側和右側分數階微分的定義分別為

式中,α∈R+,[α]是α的整數部分。

性質1[19]如果f(t)∈C[t0,∞),則

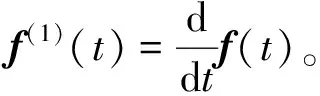
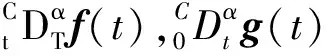
定義3[19]雙參數的Mittag-Leffler函數的定義為

特別地,當β=1時,單參數的Mittag-Leffler函數的定義為

引理3[15]設Φα,β(t)=tβ-1Eα,β(Atα),t∈[0,+∞),其中,α>0,β>0,A∈Cn×n,則

引理4[21]初值問題

等價于下面的積分方程

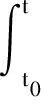
式中,A∈Cn×n,B∈Cn×p,0<α<1。

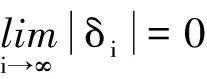
2 問題描述及分析

考慮一類分數階線性時不變系統

(1)

式中,t∈[0,T],α∈(0,1);xk(0)∈Rn,uk(t)∈Rp和yk(t)∈Rq分別為系統第k次重復操作的狀態向量、控制輸入向量和輸出向量;A∈Rn×n,B∈Rn×p和C∈Rq×n都為常數矩陣。

下面給出了分數階系統的一些基本假設。

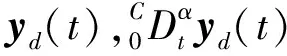
(t∈[0,T])存在,且只存在期望的控制輸入和理想狀態,使得

(2)

假設2CB為行滿秩矩陣。

對于分數階系統(1),首先考慮具有初始狀態學習的一階開環PDα-型分數階迭代學習控制算法

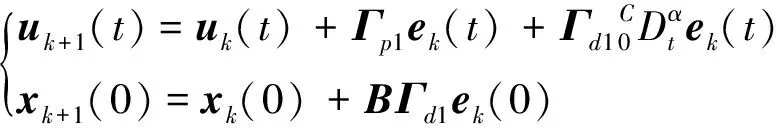
(3)

式中：Γp1和Γd1分別為比例和微分學習增益矩陣；ek(t)=yd(t)-yk(t)為系統第k次迭代時的跟蹤誤差。

眾所周知,系統運行中的反饋信息可以加速學習過程的收斂速度。因此,本文進一步研究了具有初始狀態學習的開閉環PDα-型分數階迭代學習控制算法。其表達式如下

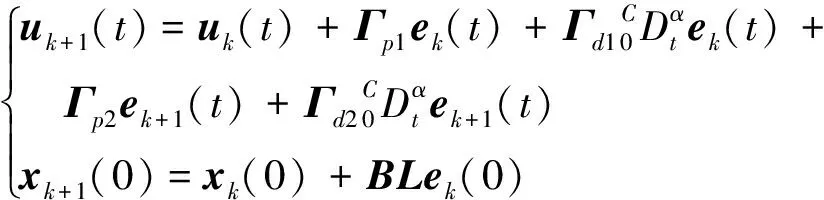
(4)

式中,L=(Γp2+Γd2),Γp2,Γd2分別為比例和微分反饋增益矩陣。

顯然,當Γp2=Γd2=0時,控制算法(4)退化為具有初始狀態學習的一階開環PDα-型算法(3)。

定理1設分數階系統(1)滿足假設1～2,當控制律(3)作用于系統(1)時,若

ρ1=‖I-CBΓd1‖+

‖Φα,α(t)(BΓp1+ABΓd1)‖1<1

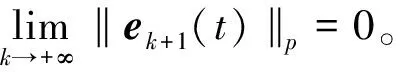
證明:根據引理4,系統(1)的狀態有如下表達式

(5)

因此

(6)

由引理2和引理3可以得到

(7)

把(7)式帶入(6)式,得

(8)

在(8)式兩邊同時取Lebesgue-p范數,采用卷積積分的廣義Young不等式,可以得到

(9)

利用定理1的條件,取k→∞得到

因此,跟蹤誤差單調收斂到零,系統的輸出在Lebesgue-p范數意義下當k→∞時的[0,T]區間內收斂到期望輸出。

定理證畢。

注1 可以看出,在Lebesgue-p范數意義下,對于具有任意初始狀態的分數階線性系統,基于初始狀態學習的開環PDα-型算法收斂的充分條件由比例學習和微分學習的學習增益矩陣確定。

注2 與λ-范數意義下的收斂條件相比,定理1中PDα-型控制算法的收斂條件相對保守,但度量跟蹤誤差不再依賴λ取值。

定理2假設分數階系統(1)滿足假設1～2,當控制算法(4)應用于系統(1)時,若滿足條件:

1)ρ0=‖I-CBL‖<1,L=Γd1+Γd2,

2)ρ2ρ1<1

式中

則

證明將(4)式與(5)式結合,得到

(10)

與(7)式的推導類似,可以得出這樣的結論

(11)

和

(12)

將(11)式和(12)式代入(10)式可得

(13)

將t=0代入(12)式可得

(14)

在(14)式兩邊同時取范數,可得

‖ek+1(0)‖≤ρ0‖ek(0)‖

(15)

式中,ρ0=‖I-CBΓd1-CBΓd2‖。

因此,根據條件1),可以得出結論

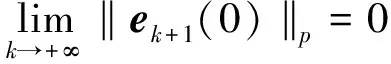
(16)

因此,表達式(13)采用這種形式

(17)

根據假設2可知,存在反饋增益微分矩陣Γd2,使得矩陣I+CBΓd2是非奇異矩陣。因此,在(17)式的兩邊左乘(I+CBΓd2)-1,兩邊同時取Lebesgue-p范數,采用卷積積分的廣義Young不等式,可得

(18)

進一步

(19)

式中

γ=

(20)

根據定理2和引理5的條件,取k→∞,可以得出以下結論

(21)

定理證畢。

注3定理2的收斂條件ρ2ρ1<1不要求滿足ρ1<1或ρ2<1。因此,在控制算法(4)中,學習增益矩陣有了更多的選擇。

注4觀察定理1和定理2的證明,控制算法的收斂條件是充分的和不必要的。即當不滿足收斂條件時,在控制算法的作用下,系統的跟蹤誤差仍可能趨于零。

注5根據定理1和定理2的收斂條件,當滿足條件ρ2ρ1<ρ1<1時,開閉環PDα-型算法(4)的收斂速度比開環PDα-型算法(3)的收斂速度快。

3 數值仿真

考慮如下分數階線性連續時不變系統

(22)

系統(22)的重復操作區間設為[0,1]:所期望的輸出為yd(t)=0.8tsin2πt,t∈[0,1]。第一次迭代的初始狀態x1(0)是隨機選擇的,但不等于期望的初始狀態xd(0)。此外,初始控制輸入u1(t)(t∈[0,1])由Rand函數隨機生成。

設置控制算法(3)的相關參數為:Γp1=0.9,Γd1=1.6,計算可得ρ1=0.893 7<1,滿足定理1的收斂條件。

為了更好地說明所提出的具有初始狀態學習的開環PDα-型算法的性能,通過對比,采用了傳統的一階開環PDα-型算法。將傳統PDα-型算法應用于具有任意初始狀態的系統(22)時,系統(22)在第4次和第12次迭代時的輸出以及從第1次迭代到第30次迭代的跟蹤誤差曲線分別如圖1和圖2所示。很明顯,隨著迭代次數的增加,系統輸出與期望輸出之間存在偏差。也就是說,系統的實際輸出不能準確地跟蹤給定的期望輸出,只能漸進地落在期望輸出的一個小鄰域內。此時,在Lebesgue-2范數和上確界范數的意義下,系統在整個區間[0,1]的跟蹤誤差都是收斂有界的。

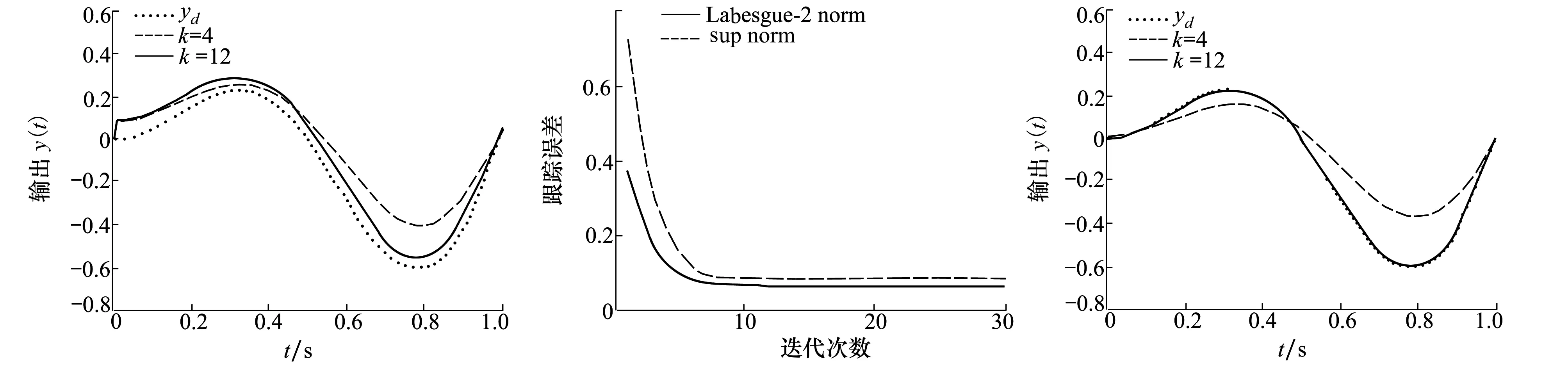
圖1 一階PDα-型控制算法跟蹤曲線 圖2 一階PDα-型控制算法的跟蹤誤差變化趨勢 圖3 初態學習的一階PDα-型控制算法跟蹤曲線

將提出的PDα-型算法(2)應用于任意初始狀態的系統(22)時,系統(22)第4次和第12次迭代的輸出如圖3所示,跟蹤誤差如圖4所示。

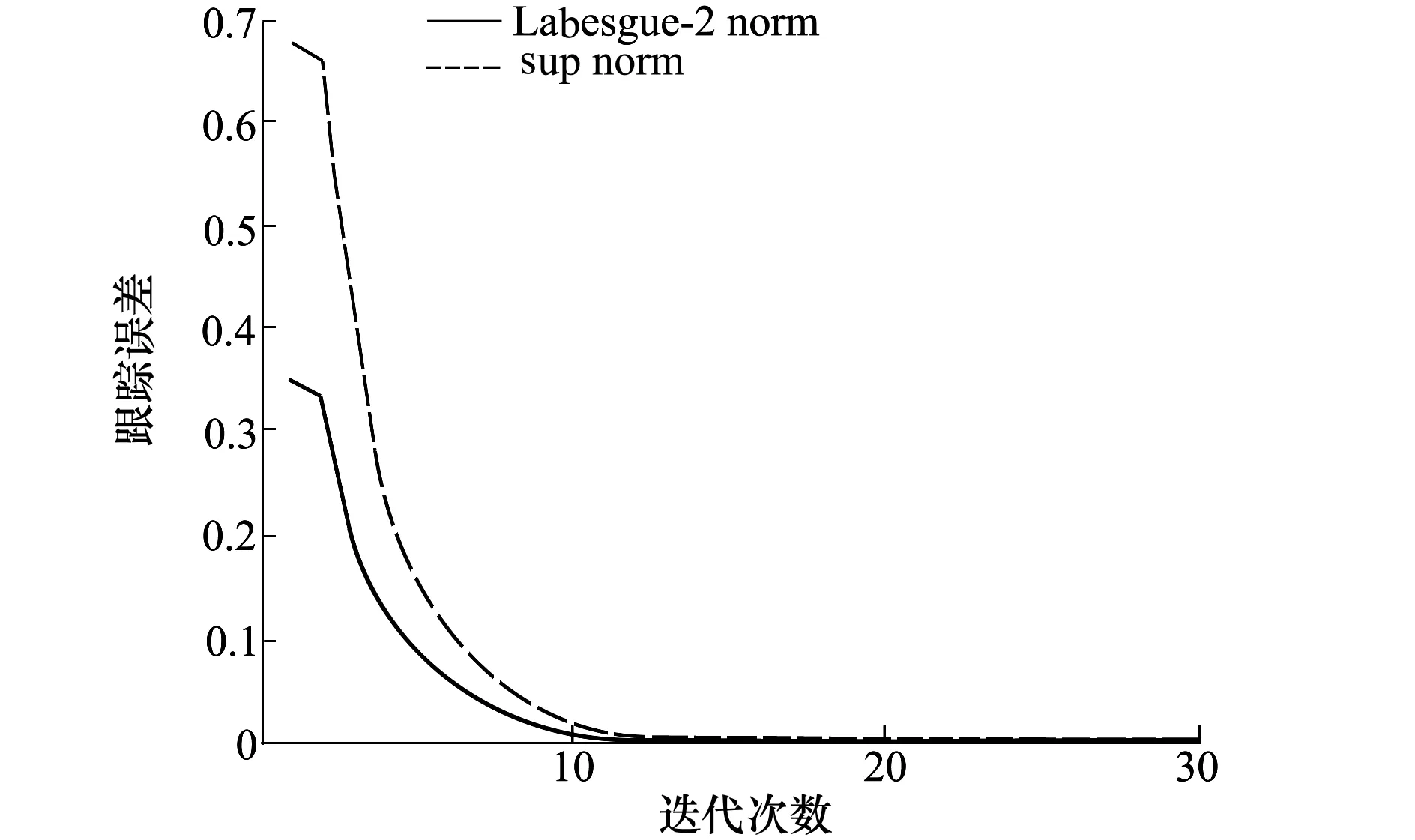
圖4 初態學習的一階PDα-型控制算法的跟蹤誤差變化趨勢

顯然,系統的輸出可以完全跟蹤期望輸出,并且跟蹤誤差隨著迭代次數的增加單調收斂到零。以上結果表明,對于具有任意初始狀態的系統(22),所提出的算法(3)是可行和有效的。

控制算法(4)的相關參數設置為:Γp1=0.9,Γd1=1.9,Γp2=0.3,Γd2=2。計算可得ρ1=0.860 1<1,ρ2ρ1=0.670 2<1,ρ2ρ1<ρ1<1。顯然,滿足定理1和定理2中的收斂條件。

在上述條件下,將本文提出的PDα-型算法(3)和(4)分別應用于任意初始狀態的系統(22),系統的跟蹤誤差如圖5所示。

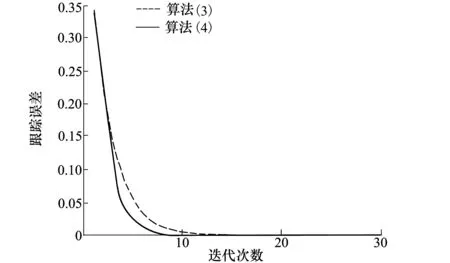
圖5 算法(3)和算法(4)跟蹤誤差比較

可以看出,在Lebesgue-2范數意義下,隨著迭代次數的增加,本文算法(3)和(4)的跟蹤誤差單調地趨于零。此時,當算法(4)迭代7次時,跟蹤誤差達到誤差范圍0.004,而算法(3)需要11次迭代才能達到上述效果。因此,在給定適當的學習增益下,算法(4)比算法(3)具有更快的收斂速度和更高的控制精度。

4 結 論

本文針對一類具有任意初始狀態的分數階線性連續系統,為了消除任意初始狀態對系統的影響,提出了帶初始狀態學習的開環和開閉環PDα-型FOILC算法。在Lebesgue-p范數意義下,利用卷積積分的廣義Young不等式,討論了PDα-型算法的收斂性。理論分析和數值仿真表明,該PDα-型算法應用于任意初始狀態系統時,隨著迭代時間的增加,跟蹤誤差單調收斂于零。

隨著迭代學習控制和分數階系統理論的進一步發展,還可以將分數階迭代學習控制應用于分布參數系統、多智能體系統和切換系統的控制之中。