新教材《4.5.1函數零點與方程的解》教學設計及反思

賈靜妍

一.教材分析

本節課是新版教材人教A版普通高中課程標準實驗教科書數學必修1第四章第4.5.1節《函數零點與方程的解》，由于學生在第二章《一元二次方程與二次函數的關系》中已經學習了零點的概念，本節課的內容就是在此基礎上的推廣。從而建立一般的函數的零點概念，進一步理解零點判定定理及其應用。培養和發展學生數學直觀、數學抽象、邏輯推理和數學建模的核心素養。

二.教學目標與核心素養

三、教學重點難點

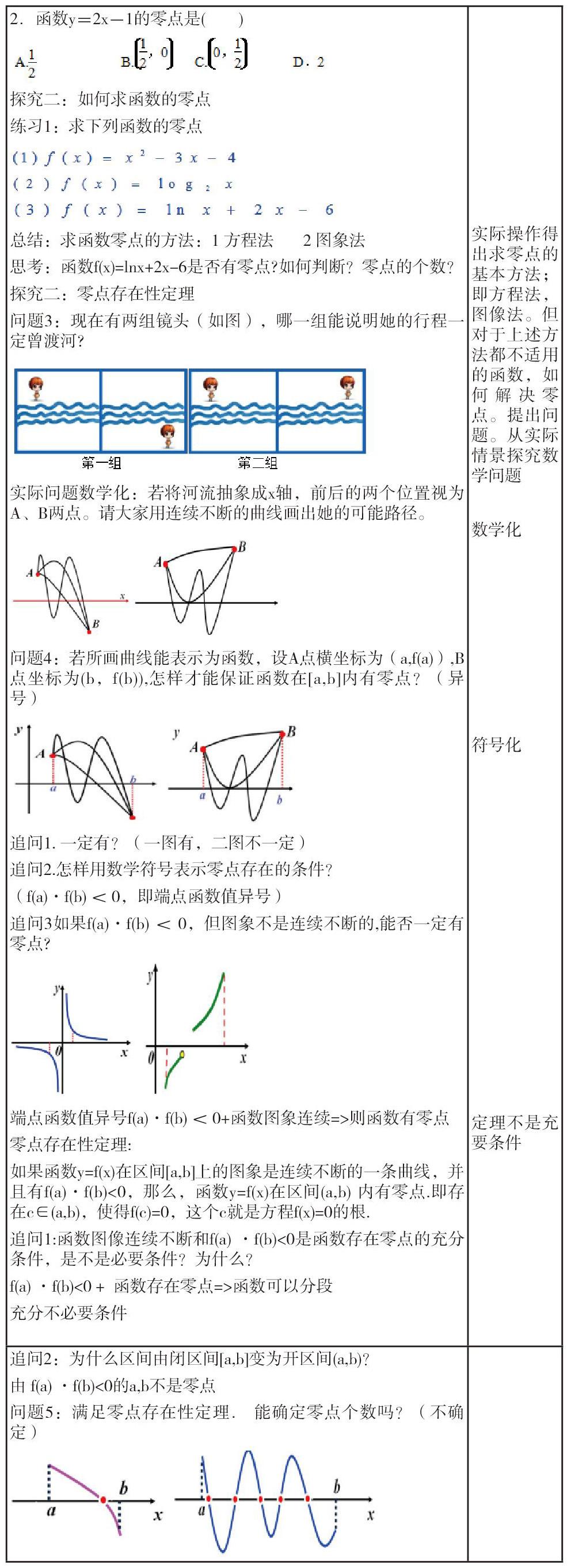
教學重點：零點的概念及存在性的判定;

教學難點：零點的確定.

四.課前準備

多媒體

五.教學過程

六.教學反思

函數零點的概念在新教材第二章《一元二次不等式的解法》中已經介紹過，所以就沒必要在重新講一次。本節內容第一個問題是函數的零點與方程的解的關系，所以結合學生的認知水平，先研究方程的解（一元一次方程，二次方程，對數方程），再畫相應的函數，觀察的出方程的解與函數圖像與x軸交點的關系，由特殊到一般，由具體到抽象，認識了函數的零點，方程的根與函數圖像與x軸交點的橫坐標的等價性。這個關系從數，形兩個角度說明了函數的零點，也是零點的本質。逐層鋪墊，降低難度。

從求函數零點的過程中發現問題，有些方程不會求解，如何解決零點，有沒有零點？有幾個？問題提出來了。 解決過程中由實際問題引出，轉化為數學問題，再進一步將數學問題符號化。同時驗證了定理的充分不必要條件，強調學生連續+異號一定有零點，反之不成立。整個過程中鍛煉了學生提出問題，分析問題，解決問題的能力，發展學生數學抽象的核心素養。

最后回到提出的問題，方程不會求解，不能求解的可以用定理法 、圖像法找到零點的區域、個數，并總結求函數零點的方法。體現了數形結合及函數與方程的思想。

不足之處：

教師講的太多，應該留給學生更多時間去參與，探究，討論，總結。

恰當使用信息技術，讓學生直觀形象的理解問題，了解知識的形成過程。信息技術要與板書相結合，這樣重點明確，過程詳細。水過留痕，比只使用課件更層次分明，重難點明確。

所有舉例反證的圖像讓學生自己動手畫。這樣他們的理解困難就會暴露出來，及時了解學情。