一種基于人體運動狀態識別的行人航跡推算方法

鄧 平，趙榮鑫，朱飛翔

（西南交通大學 信息編碼與傳輸四川省重點實驗室，成都 610097）

隨著信息技術的飛速發展和智能設備的廣泛普及，基于位置的服務（Location Based Service，LBS）逐漸成為社會生活的研究熱點[1,2]。得益于半導體技術的發展，如加速度傳感器、陀螺儀、磁力計等微型傳感器已廣泛集成于智能手機中，結合慣性導航技術，基于智能手機的行人導航定位技術受到越來越多的關注。

目前，較多的研究集中在傳感器的校準以及如何提高行人定位導航的精度，對于行人導航過程的運動行為狀態要求比較苛刻，即只能前進，難以滿足一些實際應用中可能出現的左右跨步、后退等運動狀態下定位的需求。Limin Xu 等人[3]設計了一種基于神經網絡的智能手機模式識別算法，在手持，通話及甩手模式下識別率達到99.45%，但只針對普通行走模式，并未對運動狀態進行討論。劉宇等人[4]利用人體不同運動時的初始相位來區分不同的運動狀態，在行走、后退及左右橫走下的定位誤差小于3.2%，但該運動檢測方式欠缺可靠性，檢測能力與運動初始相位強相關。Itzik Klein 等人[5]通過分析訓練集大小及數據窗口寬度，利用12 個特征實現基于口袋、手持、通話和甩手模式下95%的分類準確率。Katsuhiko Kaji 等人[6]考慮腰部的旋轉導致人體運動方向與手機方向不一致，利用加速度及角速度平面分量來抵消腰部旋轉，從而實現非直線運動狀態下的方向糾正，但針對的運動模式比較簡單，且定位的準確性難以保證。殷曉玲等人[7]提出包含行走、跑步、騎行在內的動作識別，但對于實際的二維平面內運動模式考慮并不完善。因此，完善并準確識別行人定位過程中復雜的運動狀態，并將其與行人慣性導航技術相互結合，對當前行人自主定位導航技術的發展具有重要意義。

1 基于人體運動狀態識別行人航跡推算算法框架

對于在多種運動狀態下的行人定位導航技術，傳統的行人航跡推算（Pedestrian dead reckoning,PDR）算法由于沒有對行人運動狀態進行完善的識別，因而沒有在PDR 過程中進行約束和修正，導航軌跡往往難以契合實際路線，產生不易預估的較大誤差。為此，本文充分考慮人體不同運動方式及規律，提出一種基于人體運動狀態識別的二維自主PDR 定位算法，并應用于智能手機實現行人定位，定位系統框架如圖1所示。

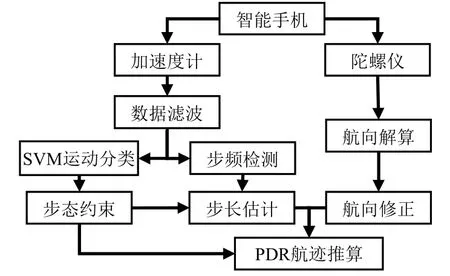
圖1 PDR 算法系統框架Fig.1 PDR algorithm system architecture

首先將二維空間內行人的運動分為行走、跑動、左跨步、右跨步和后退5 種狀態，利用智能手機作為定位設備，通過改進傳統的峰值檢測法，實現適用于復雜運動狀態的步頻檢測及計步；接著構建基于線性支持向量機（Support Vector Machine,SVM）的多分類器，完成運動狀態的初步識別；然后提出基于人體運動規律的相鄰步態約束法，對分類結果進行校正，實現高精度的運動狀態識別；最后，基于識別結果對傳統PDR 算法進行改進，并進行航向糾正，實現二維平面下基于運動狀態識別的行人導航定位。

2 改進的加速度峰值檢測

2.1 加速度數據預處理

智能手機內置加速度計的輸出頻率范圍為15-200 Hz[8]，本文采用50 Hz 作為手機輸出頻率。將采集的三軸加速度數據按式(1)合并得到合加速度模值：

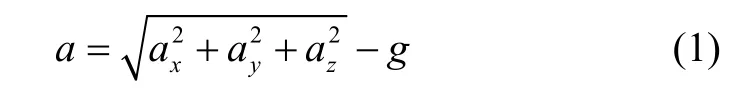
其中：a為合加速度模值；ax、ay、az分別為x軸、y軸、z軸加速度，g為重力加速度，大小為9.8 m/s2。

目前智能手機多采用價格低廉的慣性傳感器，存在較大噪聲，若將其輸出信號直接進行步態檢測則會嚴重影響計步的精度。常見的用于減小加速度計噪聲的濾波技術有低通濾波、移動均值濾波以及卡爾曼濾波等。由于理想加速度波形呈連續性變化，且加速度計主要噪聲來自于隨機噪聲，因此本文采用移動均值濾波法[9]對濾除重力的合加速度數據進行預處理。本文通過實驗結果分析，發現當濾波窗口大小N取值為3 時濾波效果最佳且不影響實際運動波形。

2.2 改進的峰值檢測法

傳統的波峰檢測法通過搜尋單步內的波峰與波谷，并利用間隔去除偽波峰/谷，再結合零點交叉法即可實現正常步態下步頻檢測，在類似于正弦波運動（如行走、慢跑）下能實現較好的檢測效果。但是，在本文所涉及的左右跨步及后退等運動狀態下，該方法檢測的運動波形通常不存在明顯的波谷，因此傳統的峰值檢測無法正確檢測步頻。為此，本文提出一種改進的單峰值檢測法及零點搜尋規則，實現基于多種運動狀態下均適用的步態檢測方法，其流程如圖2所示。

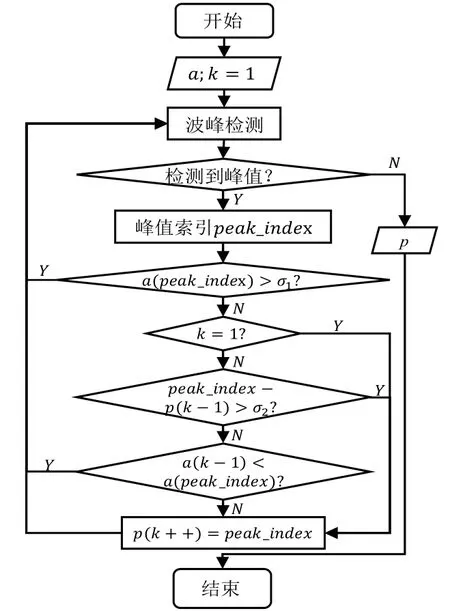
圖2 單峰值步態檢測Fig.2 Detection of single peak

1）單峰值檢測

鑒于本文所研究的部分運動狀態下合加速度波形無明顯波谷，本文采用以下單波峰檢測方法實現能通用的行人步態檢測，即舍去波谷，只需通過波峰完成單步步態檢測，如圖3 中所示。圖中，p數組表示有效波峰，k為p的索引，peak_index表示波谷所在加速度數組a中的索引。本文所設置的峰值閾值1σ為2 m/s2。波峰之間最小間隔2σ為15 個樣本間隔。

2）零點檢測的改進

步頻是步長估計需要的重要特征之一，在基于腰部的行人慣性導航技術常通過零點檢測來完成步頻的統計。本文則在單峰值檢測下進行零點判斷，以單步波峰為基準，其靠前搜尋的第一個零點即標定為該步左零點，右零點則為該步波峰靠后搜尋的第二個零點。為抑制噪聲影響，本文設置零點最大搜索范圍，左右零點最大搜索范圍分別為12 和25 個采樣點間隔。

通過多次實驗測試，本文的單波峰檢測法在本文所研究的多種運動模式下均能實現100%正確檢測率，檢測效果如圖3所示。

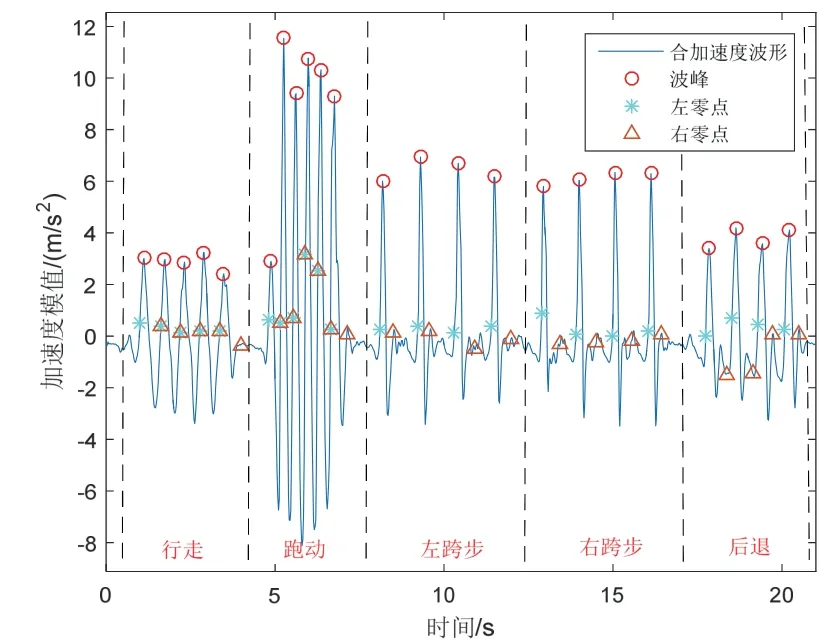
圖3 多運動步態檢測Fig.3 Detection of step

3 基于SVM 的運動狀態識別

3.1 SVM 分類器

1）線性SVM 原理

支持向量機（SVM）是一種二分類模型，由Vapnik等人提出并迅速發展起來的一種基于統計學習理論的機器學習算法，它的核心思想是通過構建超平面函數，正確地將樣本數據集進行劃分。假設現有樣本數據集其中表示第i個特征向量，表示的類標記，其符號用于區分不同實例，樣本點表示為。超平面決策邊界函數為：

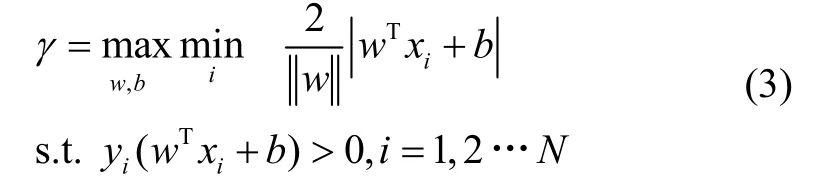
式中，γ為第i個樣本點到超平面的距離。對于滿足條件的(,)w b，還需增加邊界函數約束，防止最大分類間隔空間內存在數據點：

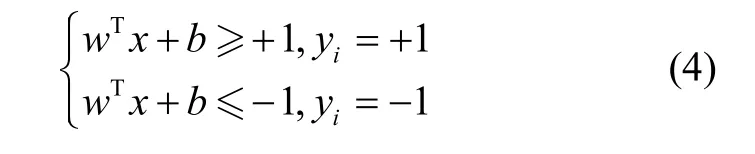
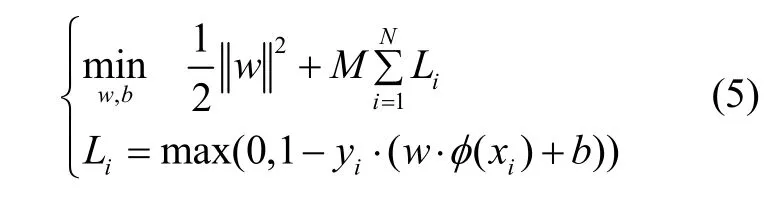
式(5)中，M為懲罰因子。同時需滿足式(6)約束條件：

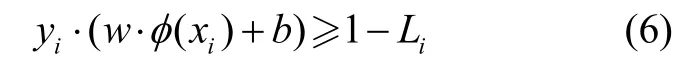
通過優化算法求解便可得到滿足最優超平面的(,)w b，即可通過式(7)進行樣本分類：

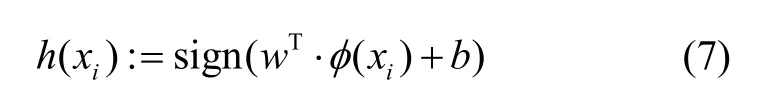
2）SVM 多分類器

鑒于本文需要實現人體多種運動狀態分類，而SVM 是一個二分類器，因此需要訓練多個SVM 模型完成多分類模型。常見的多分類方式有一對多（One-Versus-Rest，OVR）及一對一（One-Versus-One，OVO）兩種。假定有m個類，OVR 需要訓練m個二分類器，對于構建某類分類器，將其對應數據標簽設為+1，其余數據標簽設為-1，最后通過投票的方式統計得票最多的類作為此分類識別的結果；OVO 則是每兩個類都訓練一個分類器，即總分類器個數為m(m-1)/2，最終同樣通過投票的方式決定分類的結果。結合本文使用場景，OVO 在訓練單個模型時較OVR快，且在新增運動狀態時，只需要重新訓練和增加新運動樣本相關的分類器即可，因此本文選用OVO 模型解決多分類問題。

3.2 加速度時域特征分析

在這里特征指的是對數據的統計量，合適的特征選擇對分類算法起到至關重要的作用。常見的特征類型可分為時域特征、頻域特征和時頻特征。頻域特征常利用諧波分析法（如傅里葉變換）獲取，因此計算量較大，而時域特征則一般利用簡單的基本運算即可獲取。由于本文采用智能手機作為實際應用設備，考慮計算的復雜性及實時性要求，本文僅對時域特征進行提取并分析，生成特征矩陣，進而完成SVM 分類器的構建。

1）特征提取

特征選擇決定識別準度，不同分類數據只有在某種特征下存在明顯的差異才能通過數學手段將其進行區分。本文通過對加速度計輸出的三軸加速度及預處理后的合加速度進行特征提取，將均值、絕對值均值（先進行數據絕對值化再求其均值）、方差、眾數、最大值、最小值、四分位距、三四分位距、互相關系數、偏度、峰度、平均絕對誤差作為基本時域特征，通過標記F1～F47依次標記以上不同特征，每種特征按x軸、y軸、z軸和合加速度順序進行編號，其中互相關系數編號順序分別表示x軸與y軸、x軸與z軸、y軸與z軸加速度互相關系數。此外，還引入Hjorth 參數的中間變量M4[10]作為特征F48～F51，自定義x軸加速度特征(1)f作為特征F52：

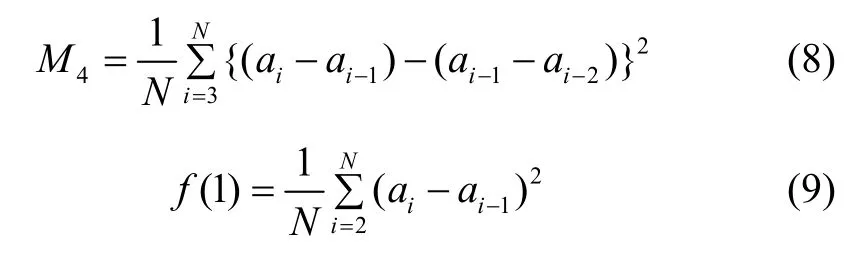
其中，N為單個窗口采樣點數，在特征分析時，每2 s時間的采樣數據作為一個窗口。

2）特征篩選

一般來說，在分類器的構建過程中，特征數量與分類識別的正確率呈正相關，但隨著特征數據量的增多，分類識別的計算復雜度也相應增加，且若存在較多無效特征，將會嚴重影響識別結果的準度。因此特征的選取對分類器的性能和分類識別的正確率至關重要。本文將上述提取的特征進行逐一篩選，將類似圖4所示能夠有效區分至少一種運動狀態的特征進行統計，如表1所示，篩選后共計特征數量為34。

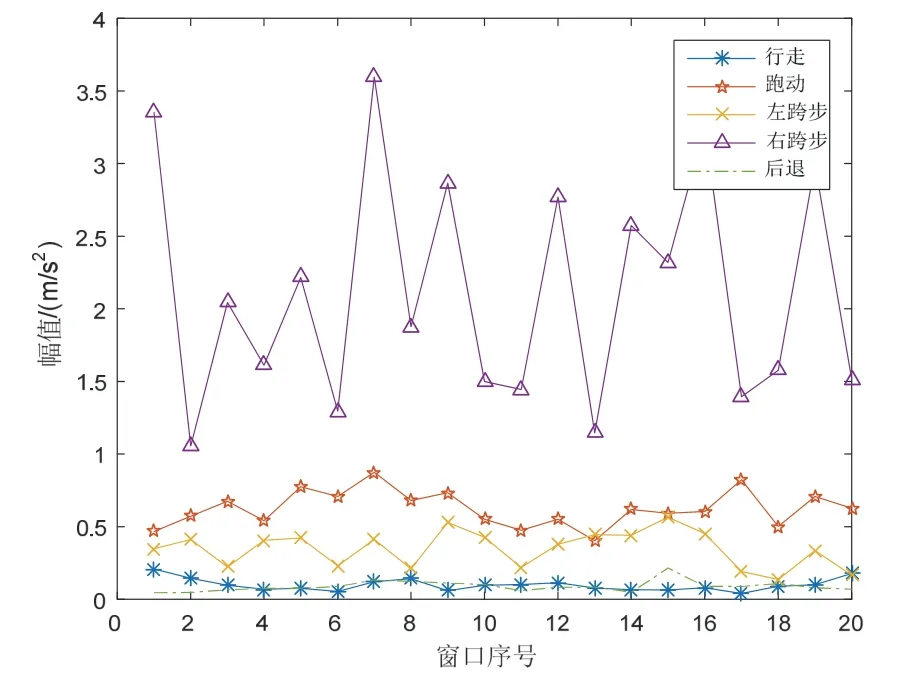
圖4 加速度x 軸(1)f 值Fig.4 (1)f for the X-axis acceleration

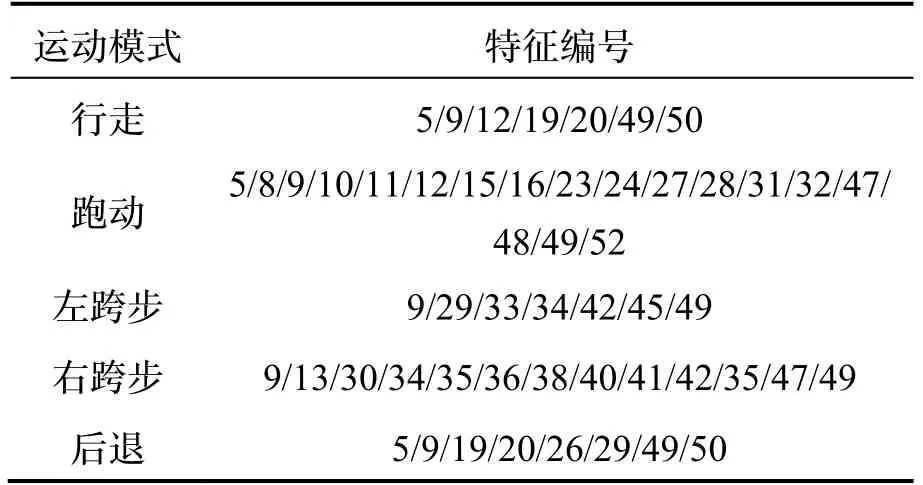
表1 有效特征Tab.1 Valid features

3.3 SVM 分類實驗及分析

特征矩陣構建完畢之后，若模型尚未建立，則進行分類模型的建立；若已存在模型，則可直接以訓練好的分類器進行分類識別，模型的建立與分類識別流程如圖5所示。

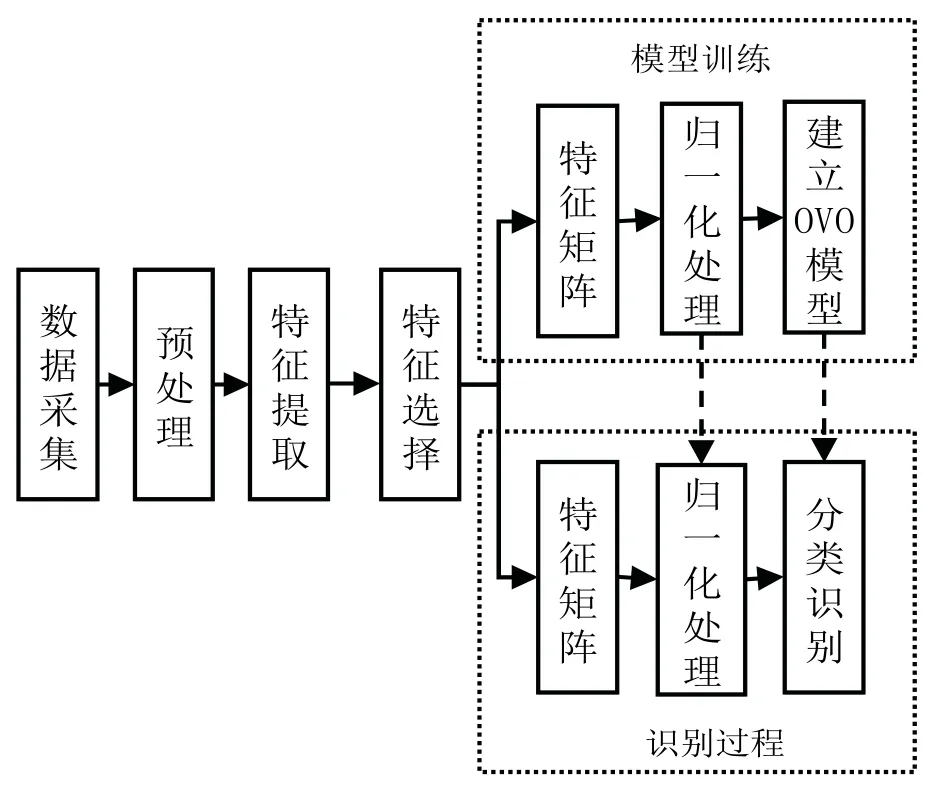
圖5 SVM 分類流程Fig.5 Classification flow chart of SVM

為了將分類算法與室內行人慣性導航技術結合，實現行人在多運動狀態下的室內定位，實際應用時手機需要動態處理傳感器采集的數據，本文研究了不同寬度的數據處理窗口對分類結果的影響，以尋找滿足定位實時性要求的最優數據處理窗口。實驗中，實驗人員共采集8 組數據，保證每組數據中每種動作狀態數據采樣時間不低于1 min，采取交叉驗證思想，根據本文所構建的SVM 多分類器得到相應分類正確率，并計算在不同窗口寬度下的平均識別正確率，如表2和圖6所示。表2 中實驗序號即代表該次實驗以此樣本作為訓練集，其余樣本為測試集。當窗口寬度大于1 s 時，識別率沒有明顯上升趨勢，平均識別率均不低于98%。考慮在實際運動場景中，單個數據窗口采樣時間內可能存在運動切換過程，但識別算法的局限性在于只能將其區間判斷為單種運動狀態。因此，數據窗口選擇時應該盡量小，通過實驗對比，本文選取的用于運動狀態分類的最優窗口寬度為1.5 s。

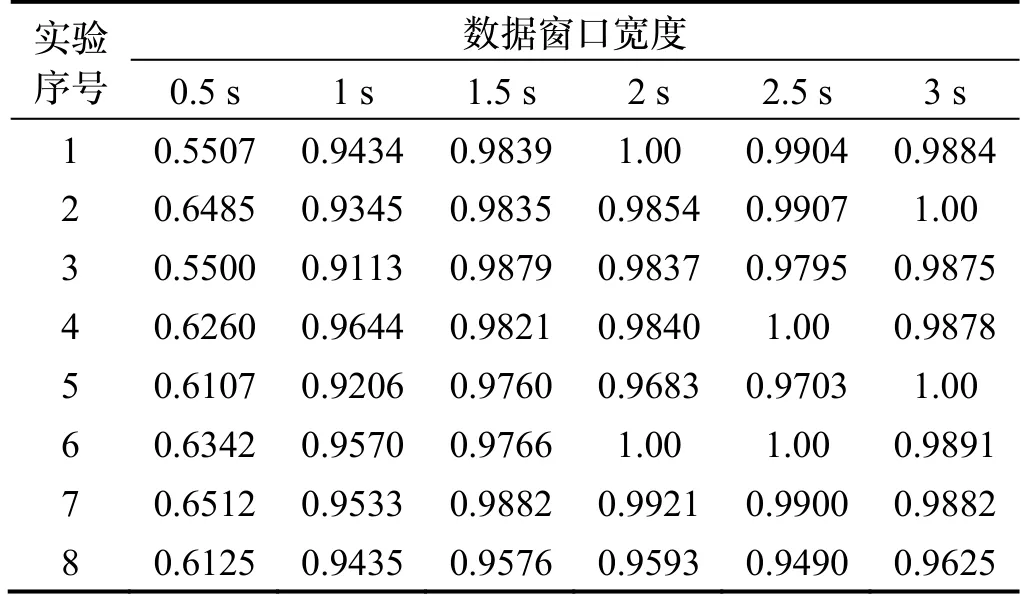
表2 運動識別的識別率Tab.2 Recognition rate of motion recognition

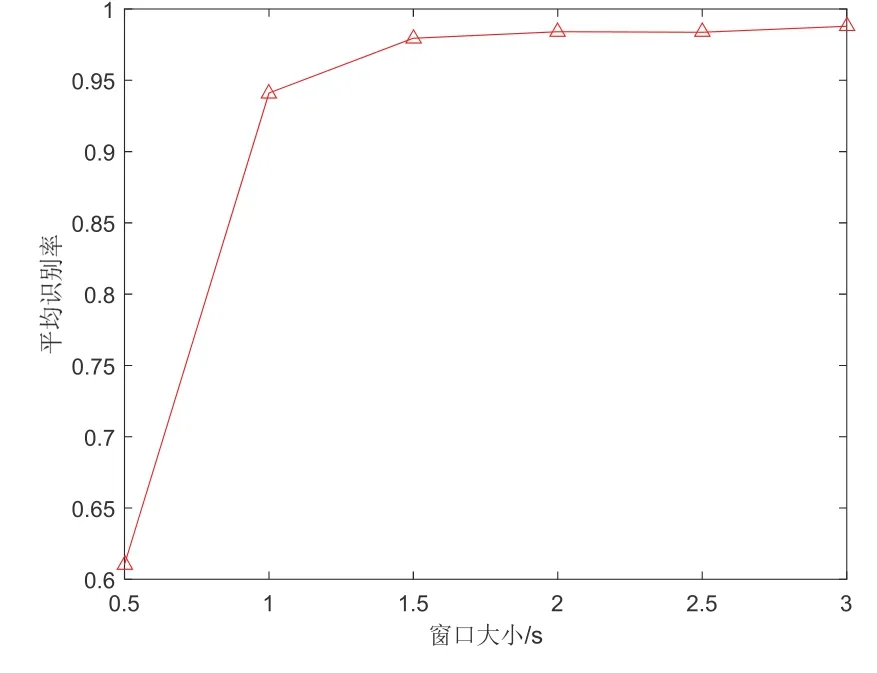
圖6 不同窗口下平均識別率Fig.6 Average recognition rate under different window sizes

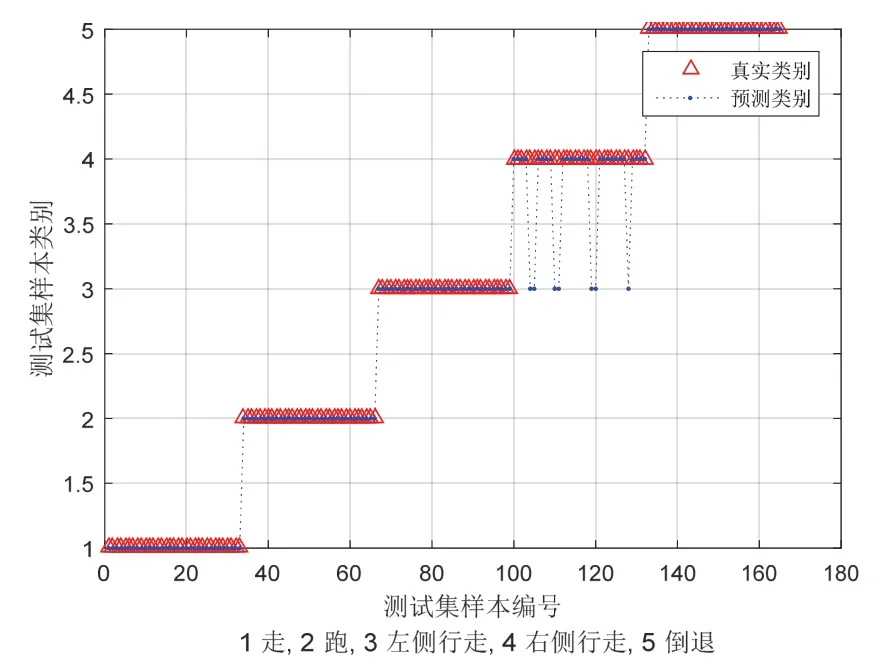
圖7 測試集SVM 預測結果對比Fig.7 SVM prediction results

3.4 相鄰步態相關性約束

本文所構建的SVM 多分類器正確識別率已達到98%以上，基本滿足運動狀態識別的要求。但就本文所研究的目標重在行人室內定位中的應用，且慣性定位技術的弱點主要在于難以有效消除累計誤差，因此高精度的運動狀態識別是實現多運動狀態下長時間室內準確定位的關鍵。圖7 是某次測試樣本的分類預測效果，在識別序列中，個別錯誤識別編號呈現突變情況，本文為此提出以下考慮人體運動規律的相鄰步態相關性約束算法，實現個別錯誤識別的糾正。

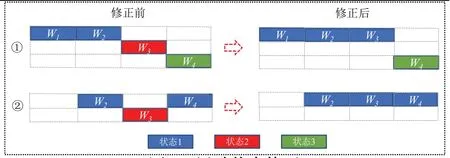
圖8 運動狀態修正Fig.8 Correction of motion state

基于行人日常運動規律，正常情況下，行人在超短時間內進行多次動作切換的概率極小，為此本文假設行人在1.5 s 的窗口大小時間內做出最多一次運動狀態切換。基于上述假設，本文采用相鄰窗口步態約束法，通過當前估計運動狀態來糾正前一窗口運動狀態，從而糾正個別編號錯誤識別。設連續相鄰的四個窗口的估計運動類型分別為W1、W2、W3、W4，當前窗口為W4，待修正窗口為W3，需修正的目標如圖8中①、②所示。W3修正條件如下：

③其余情況不進行修正。

通過步態約束，糾正前后分類識別率對比如圖9所示。糾正后，平均正確識別率達到99.37%，接近100%。

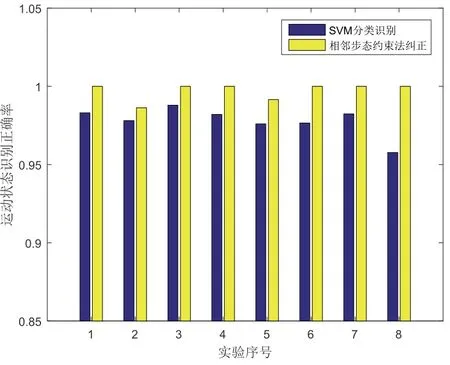
圖9 步態約束前后識別率對比Fig.9 Comparison of recognition accuracy before and after gait constraint

4 基于多運動狀態識別的行人航跡推算

傳統的PDR 算法如式(10)所示，該算法利用慣性傳感器計算人的步長和方向，從而推測行人在建筑內的蹤跡：

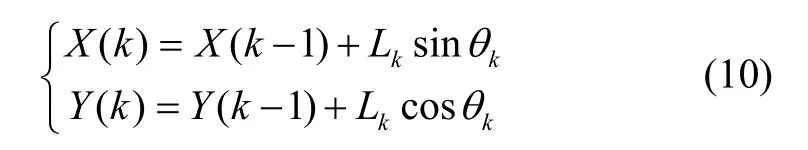
式中，()X k和()Y k表示行人第k步在二維導航平面的位置，表示第k步的航向，表示第k步的步長。結合傳統PDR 算法，本文提出式(11)所示行人多運動狀態航跡推算算法：

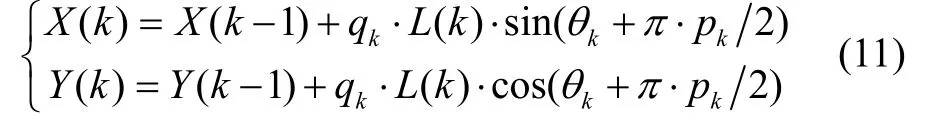
4.1 步長估計

步長是影響定位準確性的關鍵因素之一，常見步長模型包括線性步長模型、非線性步長模型和人工智能步長模型。由于人工智能步長模型計算復雜度較高，鑒于本文已通過SVM 來實現運動狀態分類，具有一定計算復雜度，因此采用計算簡單，易訓練的線性/非線性步長模型組合方式估計步長。對于行走，跨步及后退狀態均為低中速運動，步頻較低，因此采用式(12)表示的由步頻及加速度方差決定的線性步長模型。對于跑動狀態，其步頻較高，因此采用式(13)所示只由加速度極值決定的Weinberg 非線性步長模型[11]。

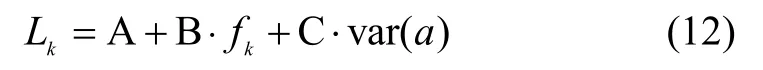
式中，L表示步長，為第k步步頻，var()a表示單步合加速度方差，A、B 和C 為常數，通過訓練得到。

4.2 航向角解算

航向角的準確解算是保證定位精度的重要因素，航向的偏差將會直接導致定位軌跡的偏移，從而嚴重影響定位的結果。四元數法計算量較余弦法和歐拉法小且精度較高，因此工程中常用來作為捷聯慣導系統姿態更新，該方法可以表示為：

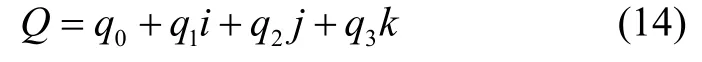
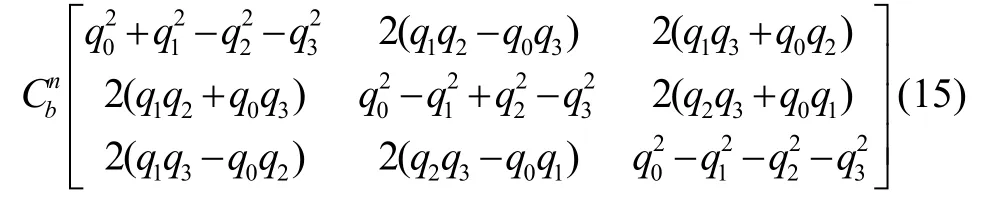
利用陀螺儀獲取角速度，通過變換矩陣得到導航坐標系下角速度數據，再將z軸角速度進行積分，即可得到航向角。由于行人手持手機時，不能總是保證手機水平放置，因此航向角與實際轉向角存在偏差。本文基于行人主要沿主航向前進的假設，引用基于緩存區改進HDE 算法[12]進行航向補償，提高航向解算的精度。在本文中，主方向區間為30°，即共設置12個主方向，反饋系數設置為0.01。

4.3 實驗驗證

本文以蘋果公司生產的iPhone 6s 作為傳感器數據采集測量工具和定位平臺，在實驗過程中，實驗者通過手持手機（具體使用方式如圖10所示）進行基于多運動狀態的定位實驗。實驗中行人運動方式包含行走、跑動、左跨步、右跨步以及倒退。

圖10 智能手機的手持方式圖Fig.10 The usage pattern of smartphone

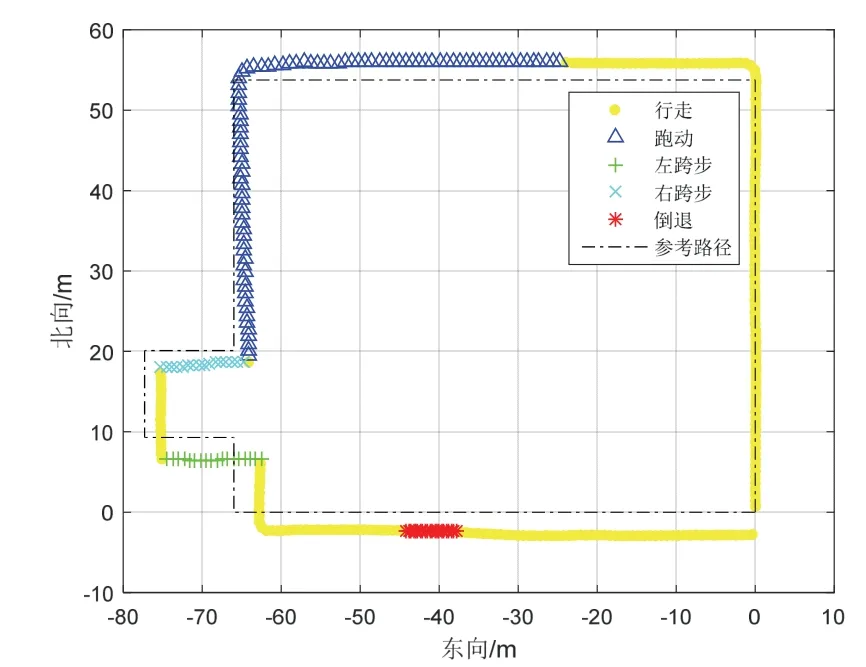
圖11 多運動下定位軌跡Fig.11 Multi motion positioning trajectory

圖11 為基于人體狀態識別的PDR 定位軌跡圖，行程為從起始點出發經矩形軌跡，最終返回起始點。從圖11 中可以看出，本文所提的運動狀態識別算法在實際定位過程中運動狀態區分度明顯，幾乎無狀態相互紊亂現象。定義定位誤差為起始點與軌跡終點之間距離占總運動距離的百分比。通過對定位結果進行誤差分析，在本文所提出的基于人體多運動狀態的PDR算法下，進行全長約262 m 的矩形路線實驗中，起始點與軌跡終點距離為3.42 m，定位誤差為1.28%。為進一步驗證本文算法的有效性和可靠性，本文分別在矩形路線以及弧形路線下進行了不同軌跡解算算法對比實驗，對比結果如圖12 和圖13所示。

圖12 和圖13 分別為矩形路線和弧形路線下不同軌跡解算算法對比圖，其參考路徑長度分別約為262 m 和400 m。從圖12、13 中可見，傳統PDR 定位算法由于沒有區分左右跨步和倒退行走等運動狀態，在矩形路線以及弧形路線下均嚴重偏離實際路線，其在矩形路線和弧形路線下的距離誤差分別為31.80 m和40.39 m，即定位誤差分別為12.14%和15.42%，均不能達到日常精確定位需求。而本文提出的基于人體多運動狀態識別的PDR 算法在矩形路線和弧形路線下的距離誤差分別為4.20 m 和5.21 m，定位誤差分別為1.60%和1.30%，遠遠低于傳統PDR 定位誤差。

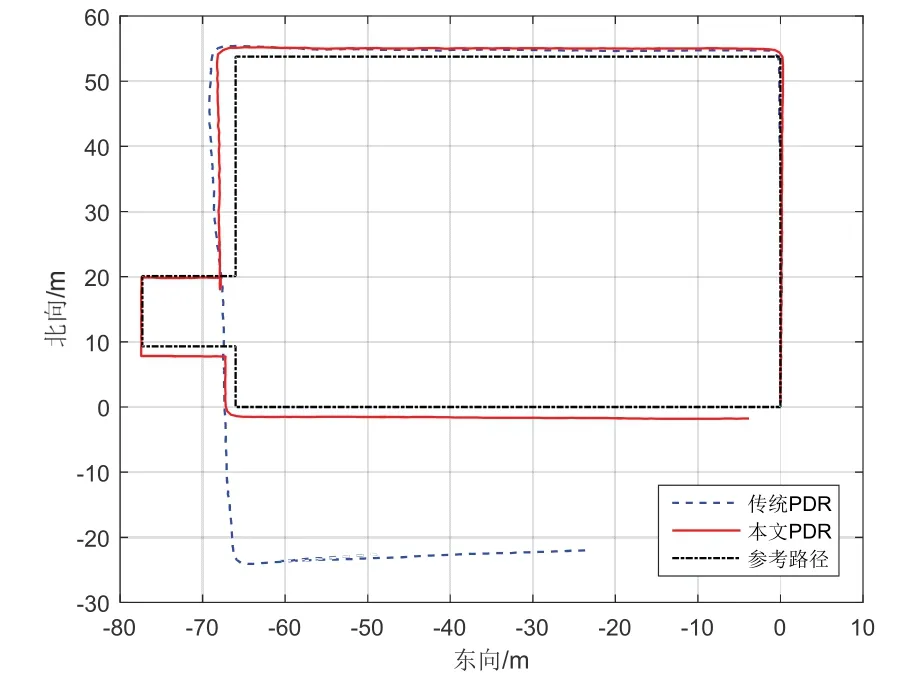
圖12 矩形場地下不同軌跡解算算法對比Fig.12 Comparison of different trajectory algorithms in rectangular field

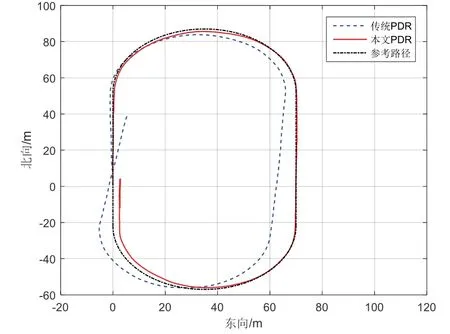
圖13 弧形場地下不同軌跡解算算法對比Fig.13 Comparison of different trajectory algorithms in arc field

5 總結

本文提出一種基于人體運動狀態識別的PDR 算法。利用智能手機作為數據采集測量工具，針對多運動狀態下傳統峰值檢測法的計步方法的不足，提出基于合加速度的單峰值檢測法，并結合改進的零點檢測法獲取精準步數及步頻。對加速度進行時域特征提取和分析，并引入額外特征，通過特征篩選，構建線性SVM 多分類器，在此基礎上提出基于行人日常運動習慣的步態約束法進行狀態識別結果糾正，從而實現高準確率的運動狀態識別。通過提出一種基于人體運動狀態識別的PDR 改進算法實現二維平面內行人精準導航定位。實驗結果證明，基于本文提出的行人運動狀態識別方法，可實現平均99.42%識別正確率，并解決了左右跨步以及倒退狀態與行走狀態難以分類識別的問題。本文最終實現在多運動狀態下定位誤差優于2%的基于人體運動狀態識別的定位算法，定位實現簡易快捷，為行人多種運動狀態下的室內準確定位導航打下了良好基礎，在消防等室內定位領域具有廣闊的應用前景。